The Gamma Operator for Big Data Summarization on

The Gamma Operator for Big Data Summarization on an Array DBMS Carlos Ordonez 1

Acknowledgments • Michael Stonebraker , MIT • My Ph. D students: Yiqun Zhang, Wellington Cabrera • Sci. DB team: Paul Brown, Bryan Lewis, Alex Polyakov 2

Why Sci. DB? • Large matrices beyond RAM size • Storage by row or column not good enough • Matrices natural in statistics, engineer. and science • Multidimensional arrays -> matrices, not same thing • Parallel shared-nothing best for big data analytics • Closer to DBMS technology, but some similarity with Hadoop • Feasible to create array operators, having matrices as input and matrix as output • Combine processing with R package and LAPACK 3

4

Old: separate sufficient statistics 5

New: Generalizing and unifying Sufficient Statistics: Z=[1, X, Y] 6

Equivalent equations with projections from Γ 7

Properties of 8

Further properties details: non-commutative and distributive 9

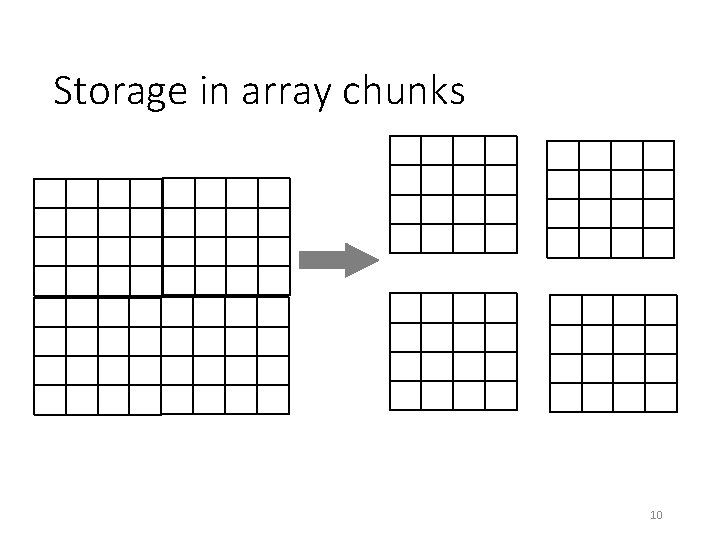
Storage in array chunks 10

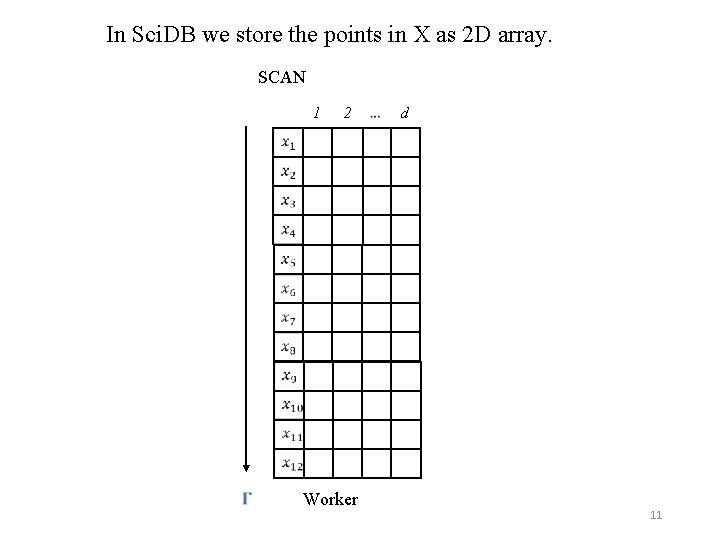
In Sci. DB we store the points in X as 2 D array. SCAN 1 2 Worker d 11

Array storage and processing in Sci. DB • Assuming d<<n it is natural to hash partition X by i=1. . n • Gamma computation is fully parallel maintaining local Gamma versions in RAM. • X can be read with a fully parallel scan • No need to write Gamma from RAM to disk during scan, unless fault tolerant 12

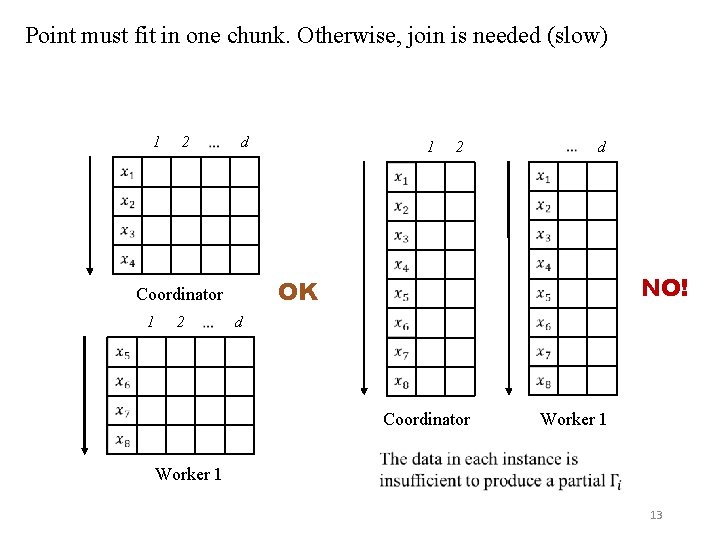
Point must fit in one chunk. Otherwise, join is needed (slow) 1 2 d 2 2 NO! d Coordinator Worker 1 d OK Coordinator 1 1 Worker 1 13

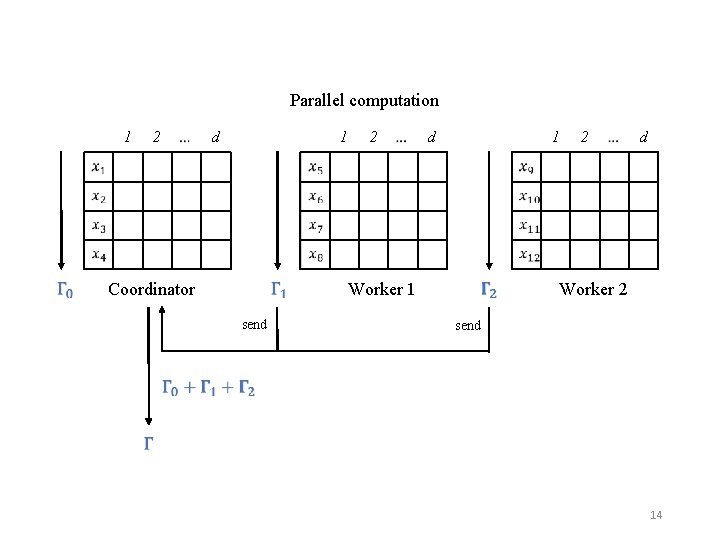
Parallel computation 1 2 d 1 Coordinator send 2 Worker 1 d 1 2 d Worker 2 send 14

Dense matrix operator: O(d 2 n) 15

Sparse matrix operator: O(d n) for hyper-sparse matrix 16

Pros: Algorithm evaluation with physical array operators • Since xi fits in one chunk joins are avoided (at least 2 X I/O with hash or merge join) • Since xi*xi. T can be computed in RAM we avoid an aggregation which would require sorting points by i • No need to store X twice: X, XT: half I/O, half RAM space • No need transpose X, costly reorganization even in RAM, especially if X spans several RAM segments • Operator works in C++ compiled code: fast; vector accessed once; direct assignment (bypass C++ functions calls) 17

System issues and limitations • Gamma not efficiently computable in AQL or AFL: hence operator is required • Arrays of tuples in Sci. DB are more general, but cumbersome for matrix manipulation: arrays of single attribute (double) • Points must be stored completely inside a chunk: wide rectangular chunks: may not be I/O optimal • Slow: Arrays must be pre-processed to Sci. DB load format, loaded to 1 D array and re-dimensioned=>optimize load. • Multiple Sci. DB instances per node improve I/O speed: interleaving CPU • Larger chunks are better: 8 MB, especially for dense matrices; avoid shuffling; avoid joins • Dense (alpha) and sparse (beta) versions 18

Benchmark: scale up emphasis • Small: cluster with 2 Intel Quadcore servers 4 GB RAM, 3 TB disk • Large: Amazon cloud 19

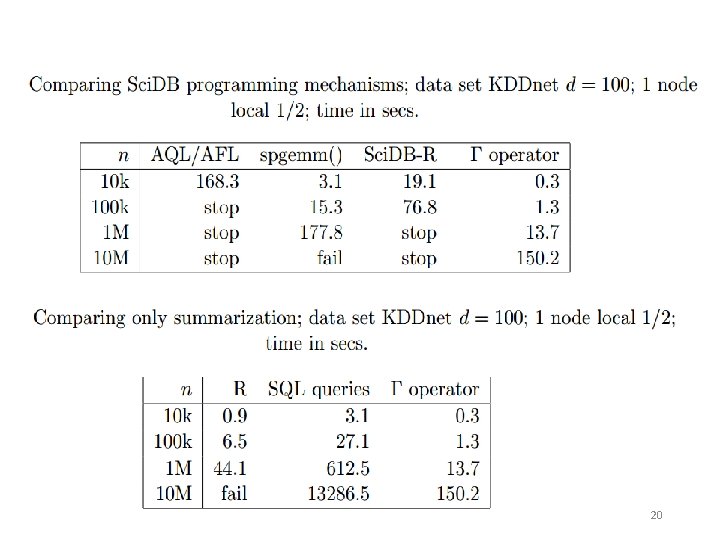
20

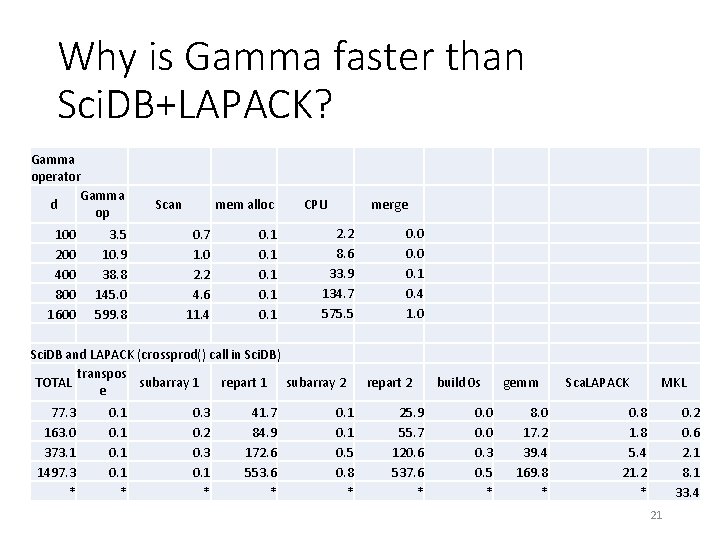
Why is Gamma faster than Sci. DB+LAPACK? Gamma operator Gamma d op Scan mem alloc CPU merge 2. 2 0. 0 3. 5 0. 7 0. 1 8. 6 0. 0 10. 9 1. 0 0. 1 33. 9 0. 1 38. 8 2. 2 0. 1 134. 7 0. 4 145. 0 4. 6 0. 1 575. 5 1. 0 599. 8 11. 4 0. 1 Sci. DB and LAPACK (crossprod() call in Sci. DB) transpos TOTAL subarray 1 repart 1 subarray 2 repart 2 build 0 s e 100 200 400 800 1600 77. 3 163. 0 373. 1 1497. 3 * 0. 1 * 0. 3 0. 2 0. 3 0. 1 * 41. 7 84. 9 172. 6 553. 6 * 0. 1 0. 5 0. 8 * 25. 9 55. 7 120. 6 537. 6 * 0. 0 0. 3 0. 5 * gemm 8. 0 17. 2 39. 4 169. 8 * Sca. LAPACK MKL 0. 8 1. 8 5. 4 21. 2 * 0. 2 0. 6 2. 1 8. 1 33. 4 21

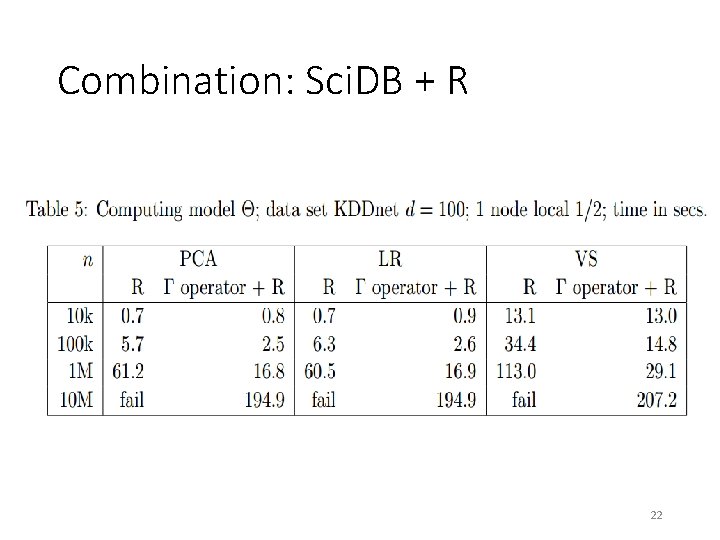
Combination: Sci. DB + R 22

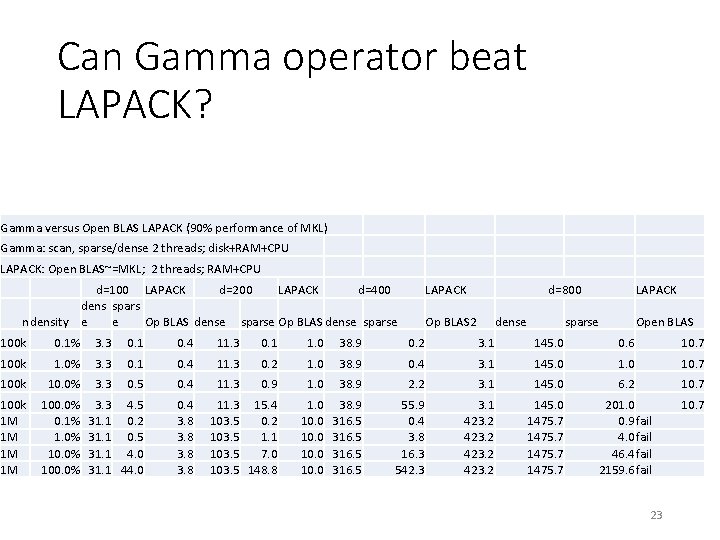
Can Gamma operator beat LAPACK? Gamma versus Open BLAS LAPACK (90% performance of MKL) Gamma: scan, sparse/dense 2 threads; disk+RAM+CPU LAPACK: Open BLAS~=MKL; 2 threads; RAM+CPU d=100 LAPACK d=200 LAPACK d=400 dens spars ndensity e e Op BLAS dense sparse LAPACK d=800 Op BLAS 2 dense LAPACK sparse Open BLAS 100 k 0. 1% 3. 3 0. 1 0. 4 11. 3 0. 1 1. 0 38. 9 0. 2 3. 1 145. 0 0. 6 10. 7 100 k 1. 0% 3. 3 0. 1 0. 4 11. 3 0. 2 1. 0 38. 9 0. 4 3. 1 145. 0 10. 7 100 k 10. 0% 3. 3 0. 5 0. 4 11. 3 0. 9 1. 0 38. 9 2. 2 3. 1 145. 0 6. 2 10. 7 100 k 1 M 1 M 100. 0% 0. 1% 1. 0% 100. 0% 3. 3 4. 5 31. 1 0. 2 31. 1 0. 5 31. 1 4. 0 31. 1 44. 0 0. 4 3. 8 11. 3 15. 4 103. 5 0. 2 103. 5 1. 1 103. 5 7. 0 103. 5 148. 8 1. 0 10. 0 38. 9 316. 5 55. 9 0. 4 3. 8 16. 3 542. 3 3. 1 423. 2 145. 0 1475. 7 201. 0 0. 9 fail 4. 0 fail 46. 4 fail 2159. 6 fail 10. 7 23

outdated Sci. DB in the Cloud: massive parallelism 24

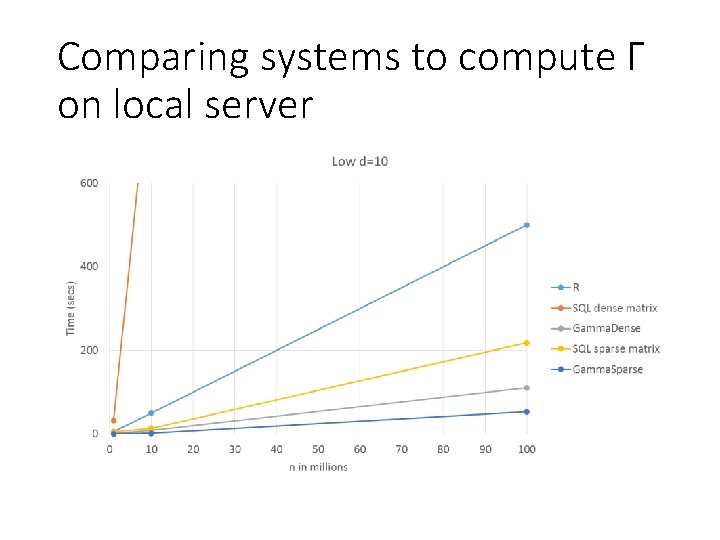
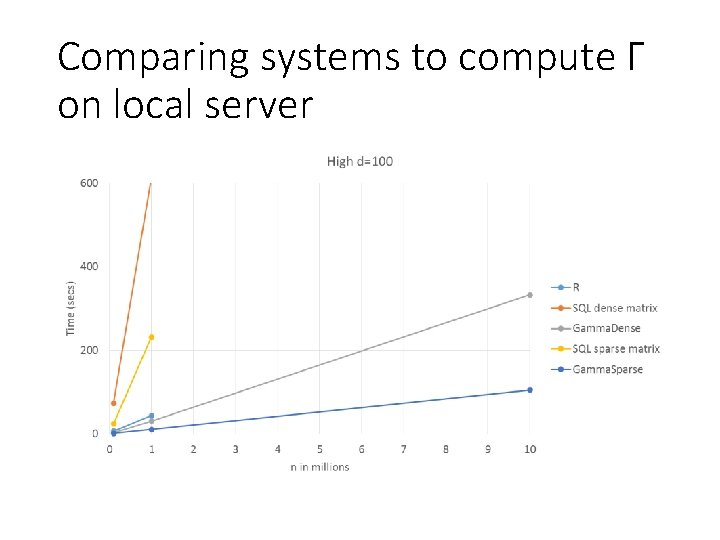
Comparing systems to compute Γ on local server

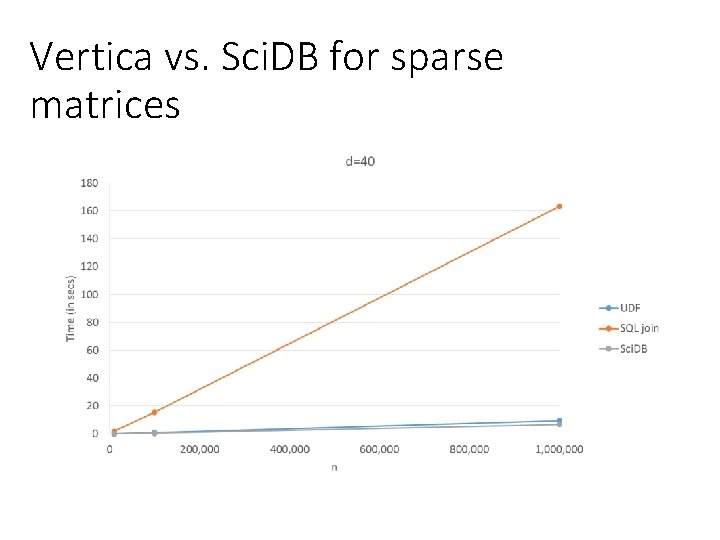
Vertica vs. Sci. DB for sparse matrices

Running on the cloud •

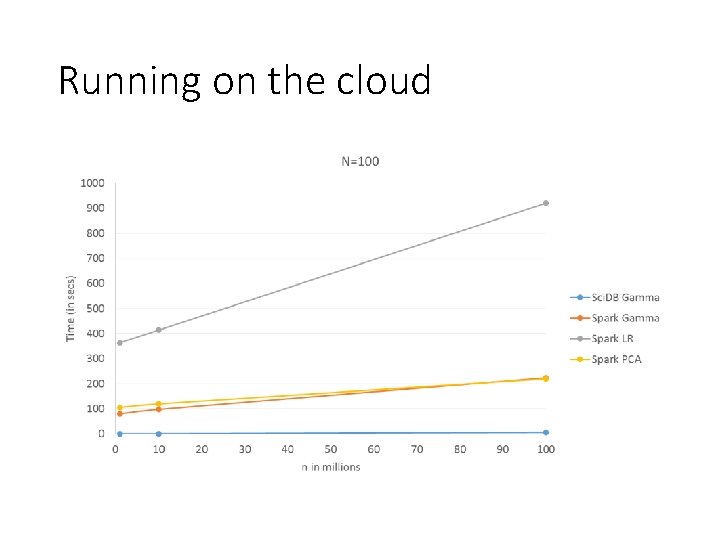
Running on the cloud

Conclusions • One pass summarization matrix operator: parallel, scalable • Optimization of outer matrix multiplication as sum (aggregation) of vector outer products • Dense and sparse matrix versions required • Operator compatible with any parallel shared-nothing system, but better for arrays • Gamma matrix must fit in RAM, but n unlimited • Summarization matrix can be exploited in many intermediate computations (with appropriate projections) in linear models • Simplifies many methods to two phases: 1. 2. Summarization Computing model parameters • Requires arrays, but can work with SQL or Map. Reduce 30

Future work: Theory • Use Gamma in other models like logistic regression, clustering, Factor Analysis, HMMs • Connection to frequent itemset • Sampling • Higher expected moments, co-variates • Unlikely: Numeric stability with unnormalized sorted data 31

Future work: Systems • DONE: Sparse matrices: layout, compression • DONE: Beat LAPACK on high d • Online model learning (cursor interface needed, incompatible with DBMS) • Unlimited d (currently d>8000); join required for high d? Parallel processing of high d more complicated, chunked • Interface with BLAS and MKL, not worth it? • DONE: Faster than column DBMS for sparse? 32