The Game of Nim on Graphs Nim G

















- Slides: 31

The Game of Nim on Graphs: Nim. G Gwendolyn Stockman Alan Frieze and Juan Vera

The Game of Nim l 2 players l n piles of disks, with a 1, a 2, … an disks on each pile l Players take turns removing disks from each pile l A player loses when there are no disks left

Impartial Games l Geography, Nim, and Nim. G are impartial games l A game in which the only difference between the two players is which one goes first l Every position of an impartial game has a Grundy Number or Nim-Value

Sprague-Grundy Numbers (Nim-Sums) Used to represent wining and losing positions l Given a game tree T = (V, E) l Recursively define: l x with l y A player is in a winning position if at the end of his/her turn the playing piece is on such that w z

Grundy Numbers (cont. ) Let a 1, a 2, … an be the binary representations of the number of disks on each of the n piles l In the game of Nim the Grundy number for a setup is the bit-wise sum (mod 2) of the ai‘s l Example: l 1 10 11 00 The Grundy number is 0 so this is a winning position!

Proposed Versions of Nim. G 2 players 1 piece is moved along an undirected graph with no selfloops, and discs are removed l If discs on vertices: l l ¡ ¡ Could move first and then remove discs Could remove discs and then move l l If discs on edges: ¡ l l Possibly allow moves to empty verticies Remove discs as you go along an edge Players take turns removing disks from piles How to win: ¡ The other player can’t complete their turn

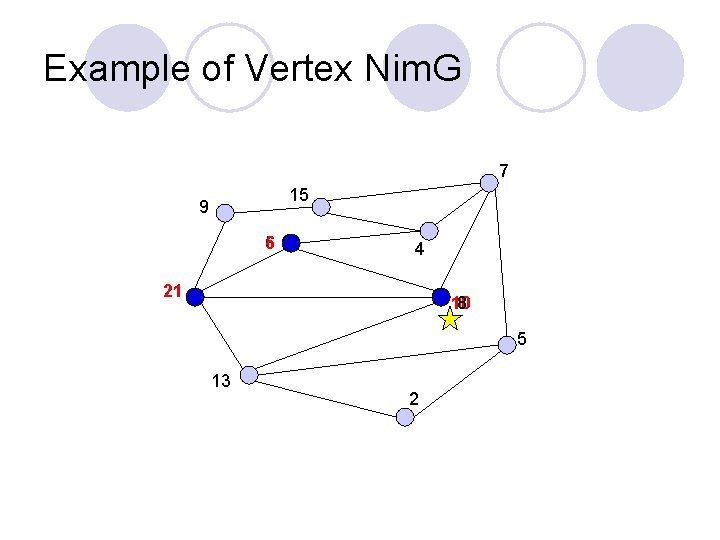
Example of Vertex Nim. G 7 15 9 5 6 4 21 10 8 5 13 2

Geography Two players alternately move a piece on a graph until one loses by being unable to make an legal moves l Directed or Undirected l Edge Geography l ¡ l Vertex Geography ¡ l No edge repeated No vertex repeated Undirected Vertex Geography ¡ Contained in a version of Vertex Nim. G with: l l ¡ Solvable in polynomial Time l l 1 chip on each vertex Not allowed to move to empty vertices Second player has a winning strategy IFF the graph has a perfect matching (Fraenkel 1993) Undirected Edge Geography ¡ PSPACE-complete (Fraenkel 1993)

Previous Work: Nim on Graphs In A Nim game played on Graphs I and II (Fukuyama 2003) Edge Nim. G was examined l Proved that the Grundy Numbers can be found completely on: ¡ Bipartite Graphs ¡ Trees ¡ Cycles l Main Method: matchings on graphs l Contains normal Nim l ¡ l 2 vertices with n edges with a 1, a 2, … an disks on each edge Contains Undirected Edge Geography ¡ 1 disk on each edge

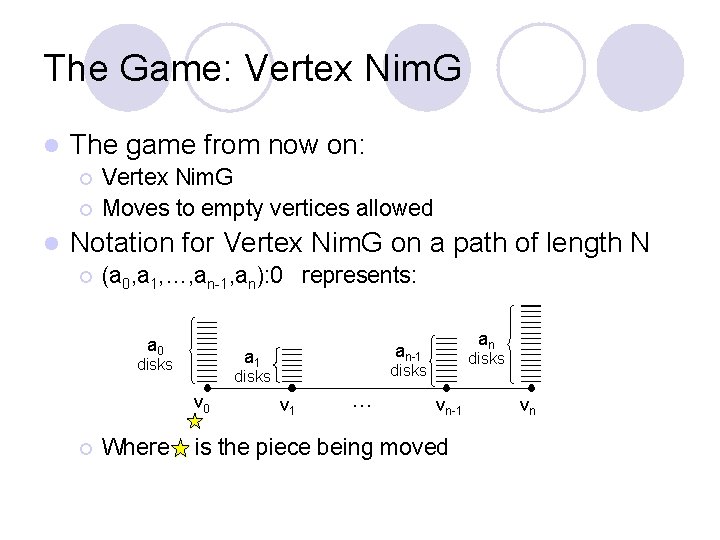
The Game: Vertex Nim. G l The game from now on: ¡ ¡ l Vertex Nim. G Moves to empty vertices allowed Notation for Vertex Nim. G on a path of length N ¡ (a 0, a 1, …, an-1, an): 0 represents: a 0 a 1 disks ¡ Where disks v 0 an an-1 v 1 … vn-1 is the piece being moved vn

Theorem 1: Vertex Nim. G on path of length 2

Nim. G on a Path of Length 3 Not so simple on longer paths l Grundy Numbers bounded by a function of d, the number of disks on the graph l First note that x l ¡ Easy to see that l ¡ and Easy to see that l ¡ is a child for is a child and 0 Rest omitted for brevity 0 x x 0 0 0 x 0

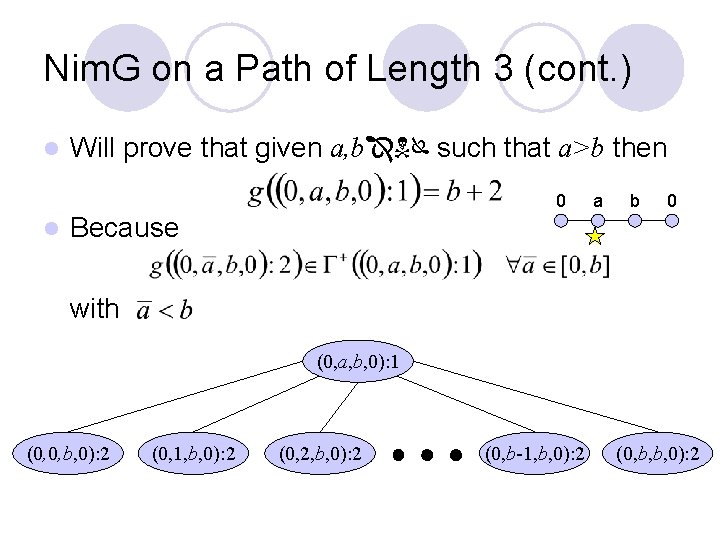
Nim. G on a Path of Length 3 (cont. ) l Will prove that given a, b such that a>b then 0 l a b 0 Because with (0, a, b, 0): 1 (0, 0, b, 0): 2 (0, 1, b, 0): 2 (0, 2, b, 0): 2 (0, b-1, b, 0): 2 (0, b, b, 0): 2

Nim. G on a Path of Length 3 (cont. ) l Take a and we want to know the value of l Examine the children of that position in the game tree and find a+1 a 1 1

Nim. G on a Path of Length 3 (cont. ) l Take a and we want to know the value of l Examine the children of that position in the game tree and find a+2 a+1 1 2 2

Nim. G on a Path of Length 3 (cont. ) l So given a, b such that a>b then (0, a, b, 0): 1 1 (0, 0, b, 0): 2 3 (0, 1, b, 0): 2 4 (0, 2, b, 0): 2 2 b+1 (0, b-1, b, 0): 2 (0, 1, b, 0): 0 (0, b, b, 0): 2 0 And l Further suppose we have a, b, c, e {0} such that l then

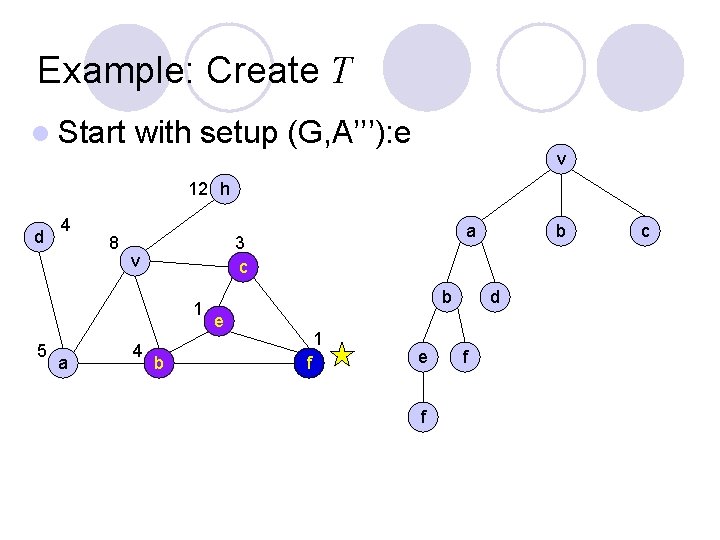
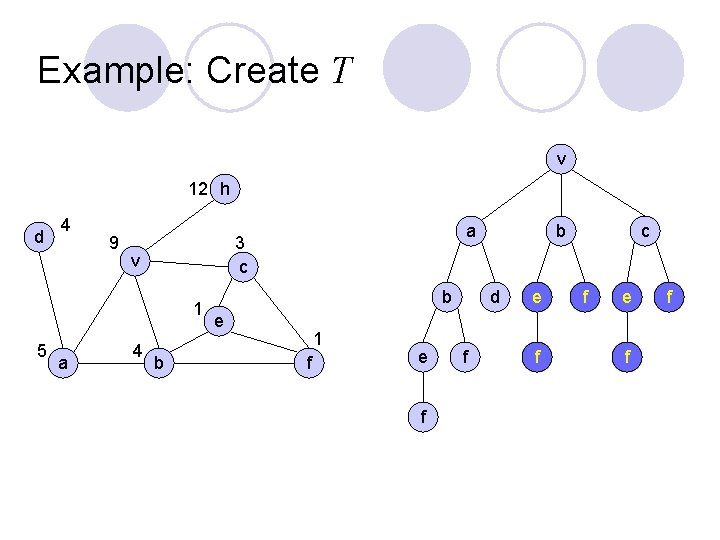
Vertex Nim. G on Any Graph Represent positions of Nim. G as (G, A): v where G is the graph, A is the amount function for G, and marker is at vertex v V(G) l A reduced game tree is used to find if a winning strategy exists from a given position, and if one does, what it is l Create the reduced game tree, T, where each node is a position, by l ¡ ¡ making (G, A): v the root For each u N(v) such that A(u)< A(v) add node (G, A’): u as a child to (G, A): v where u v x ¡ Repeat once for each node added to T (G, A’): u (G, A): v y

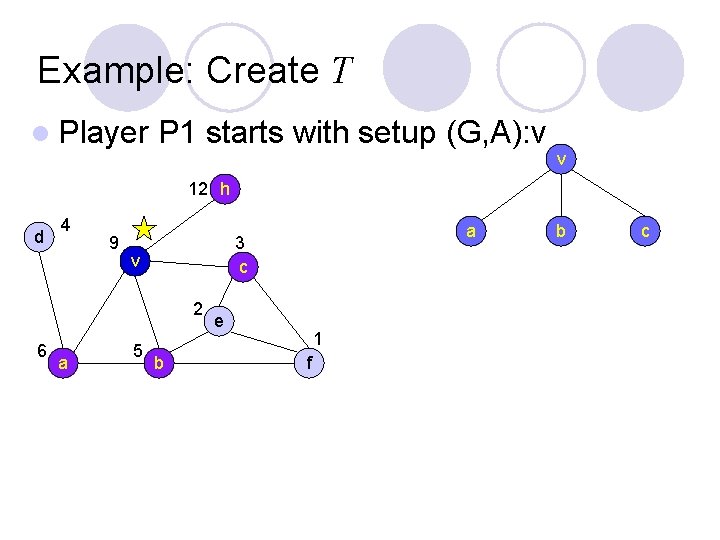
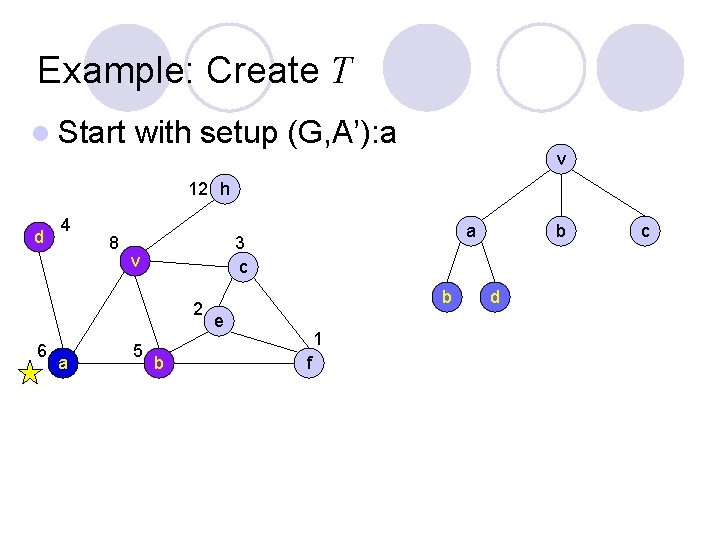
Example: Create T l Player P 1 starts with setup (G, A): v v 12 h d 4 9 v 2 6 a 5 a 3 c b e 1 f b c

Example: Create T l Start with setup (G, A’): a v 12 h d 4 8 v 2 6 a 5 b b a 3 c b e 1 f d c

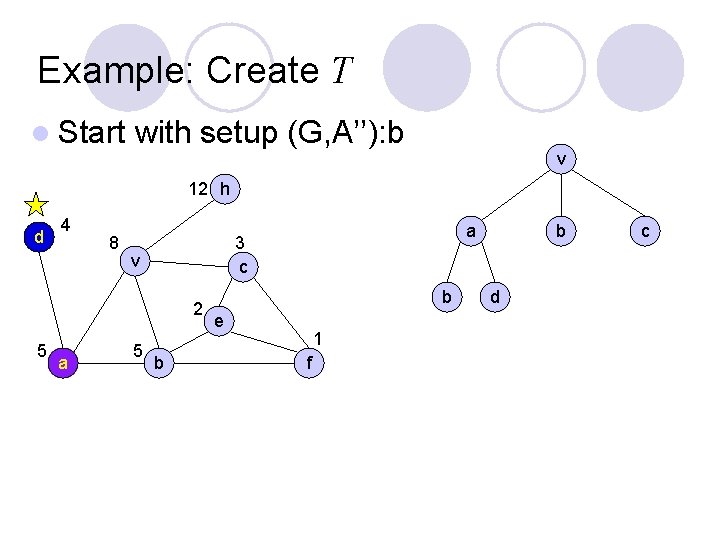
Example: Create T l Start with setup (G, A’’): b v 12 h d 4 8 v 2 5 a 5 b b a 3 c b e 1 f d c

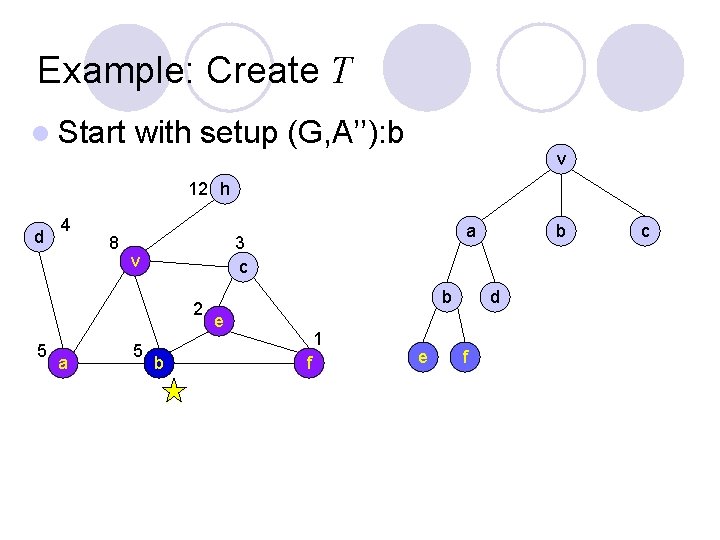
Example: Create T l Start with setup (G, A’’): b v 12 h d 4 8 v 2 5 a 5 b b a 3 c b e 1 f e d f c

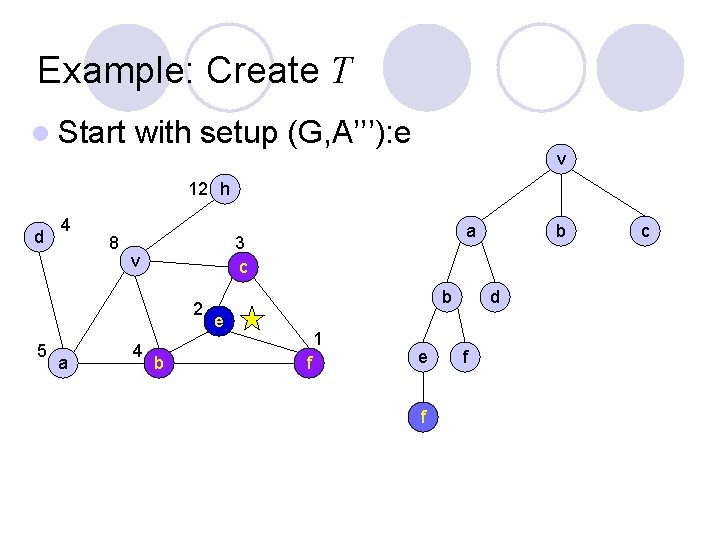
Example: Create T l Start with setup (G, A’’’): e v 12 h d 4 8 v 2 5 a 4 b b a 3 c b e 1 f e f d f c

Example: Create T l Start with setup (G, A’’’): e v 12 h d 4 8 v 1 5 a 4 b b a 3 c b e 1 f e f d f c

Example: Create T v 12 h d 4 9 v 1 5 a 4 b b a 3 c b e 1 f e f d f e f c f e f f

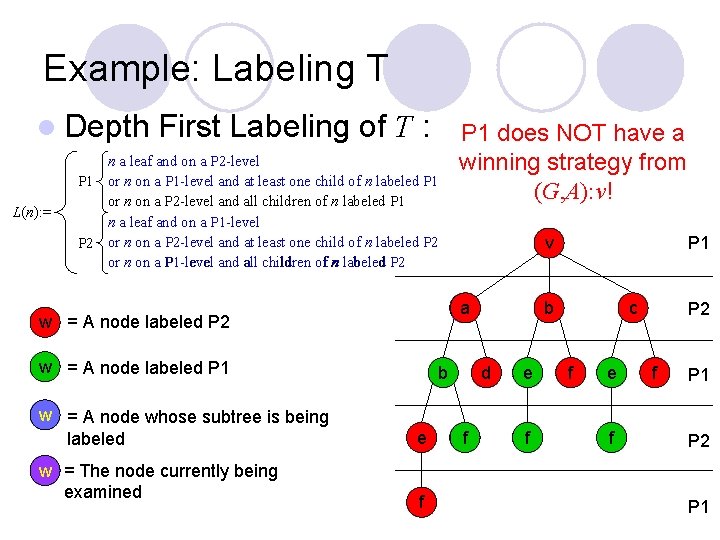
Labeling T If it is player P 1’s turn then label all even levels, including 0, of T, P 1, and all odd levels P 2 l Label each node either P 1 or P 2 l ¡ ¡ l Label all n V(T), with labeling function L: V(T) {P 1, P 2}, using a depth first labeling starting with the n=root of V(T) ¡ ¡ l Player P 1 has a winning strategy from nodes labeled P 1 Player P 2 has a winning strategy from nodes labeled P 2 Apply the depth first labeling to all children of n in T Label n with L(n) The root of T is labeled P 1 IFF there is a winning strategy for player P 1

Example: Labeling T l Depth L(n): = First Labeling of T : n a leaf and on a P 2 -level P 1 or n on a P 1 -level and at least one child of n labeled P 1 or n on a P 2 -level and all children of n labeled P 1 n a leaf and on a P 1 -level P 2 or n on a P 2 -level and at least one child of n labeled P 2 or n on a P 1 -level and all children of n labeled P 2 w = A node labeled P 1 w = The node currently being examined v a w = A node labeled P 2 w = A node whose subtree is being labeled P 1 does NOT have a winning strategy from (G, A): v! b e f c b d f P 1 e f f e f P 2 f P 1 P 2 P 1

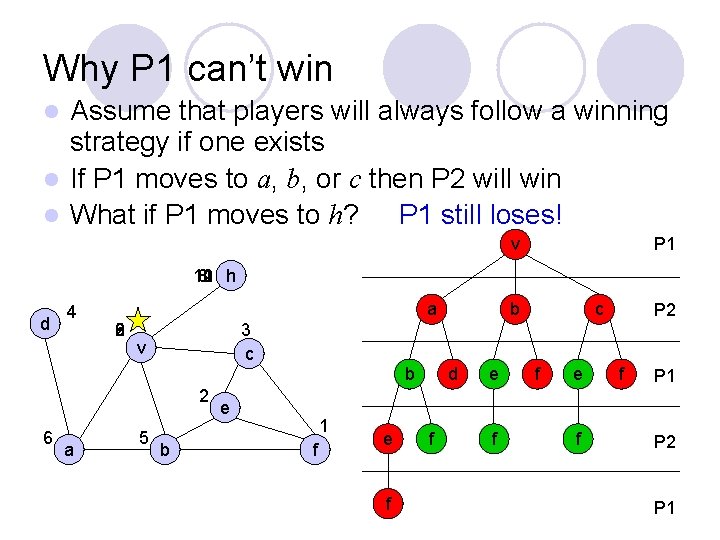
Why P 1 can’t win Assume that players will always follow a winning strategy if one exists l If P 1 moves to a, b, or c then P 2 will win P 1 still loses! l What if P 1 moves to h? l v P 1 12 11 10 8 h d 4 a 9 8 6 2 5 v 2 a 5 c P 2 3 c b 6 b b e 1 f e f d f e f f P 1 P 2 P 1

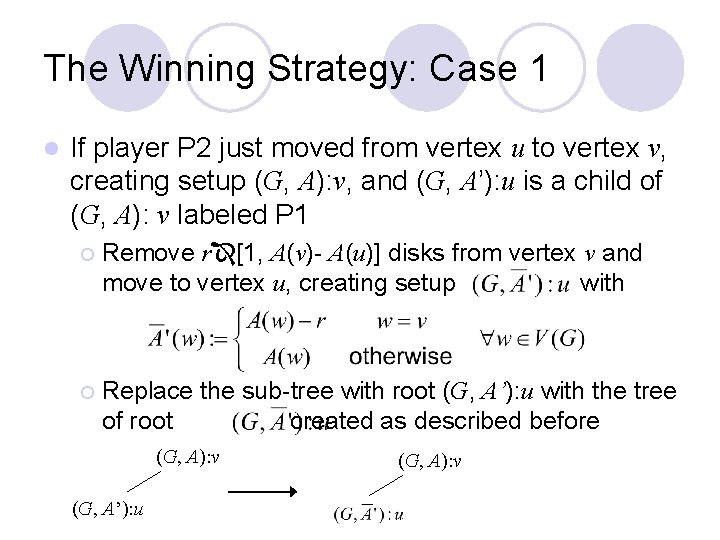
The Winning Strategy: Case 1 l If player P 2 just moved from vertex u to vertex v, creating setup (G, A): v, and (G, A’): u is a child of (G, A): v labeled P 1 ¡ Remove r [1, A(v)- A(u)] disks from vertex v and move to vertex u, creating setup with ¡ Replace the sub-tree with root (G, A’): u with the tree of root created as described before (G, A): v (G, A’): u (G, A): v

The Winning Strategy: Case 2 l l Otherwise, given setup (G, A): v pick any child (G, A’): u of node (G, A): v in T that is labeled P 1 ¡ remove r [1, A(v)- A(u)] disks from vertex v and move to vertex u, creating setup with ¡ Replace the sub-tree with root (G, A’): u with the tree of root created as described before The alterations to T insure that T maintains the property that for any node y=(G, A): w V(T) (G, A): w (G, A’): x

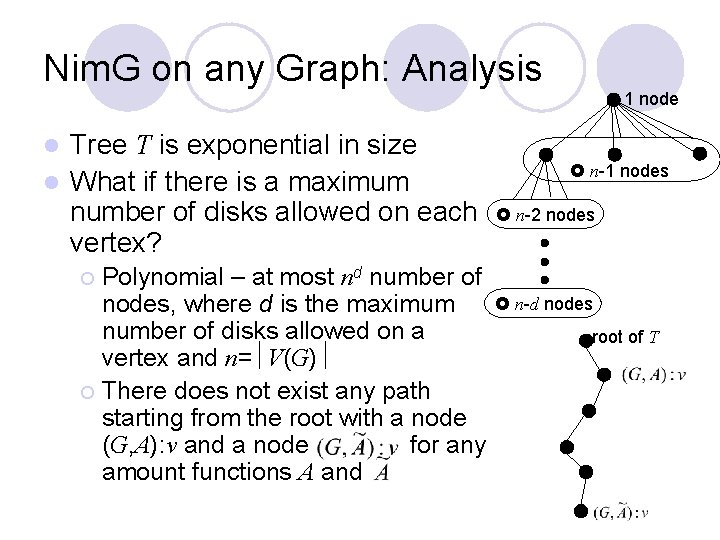
Nim. G on any Graph: Analysis Tree T is exponential in size l What if there is a maximum number of disks allowed on each vertex? 1 node l n-1 nodes n-2 nodes Polynomial – at most nd number of n-d nodes, where d is the maximum number of disks allowed on a root of T vertex and n= V(G) ¡ There does not exist any path starting from the root with a node (G, A): v and a node for any amount functions A and ¡

Questions? ? ?