The Four Dimensional World Spacetime a piece of

The Four Dimensional World Spacetime: a piece of Einstein’s General Theory of Relativity

The Definition of a Clock A motion that repeats itself with a non-varying pattern • The second hand of a clock or watch • A pendulum • A digital stopwatch Another type of clock: A light beam bouncing between two parallel mirrors

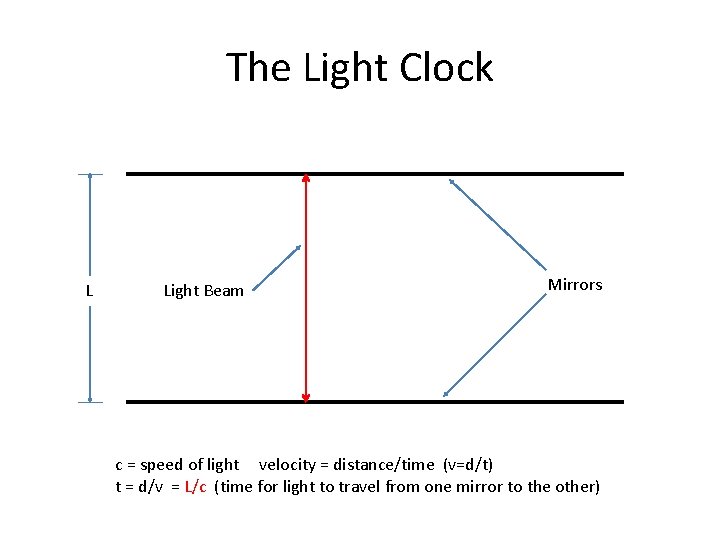
The Light Clock L Light Beam Mirrors c = speed of light velocity = distance/time (v=d/t) t = d/v = L/c (time for light to travel from one mirror to the other)

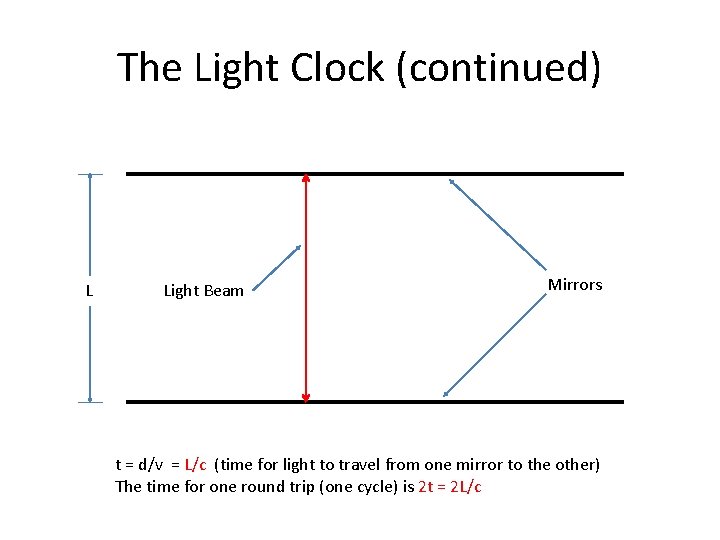
The Light Clock (continued) L Light Beam Mirrors t = d/v = L/c (time for light to travel from one mirror to the other) The time for one round trip (one cycle) is 2 t = 2 L/c

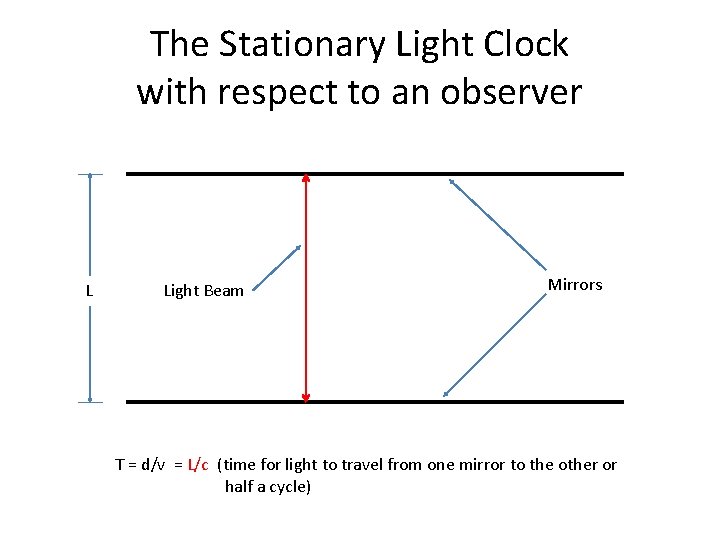
The Stationary Light Clock with respect to an observer L Light Beam Mirrors T = d/v = L/c (time for light to travel from one mirror to the other or half a cycle)

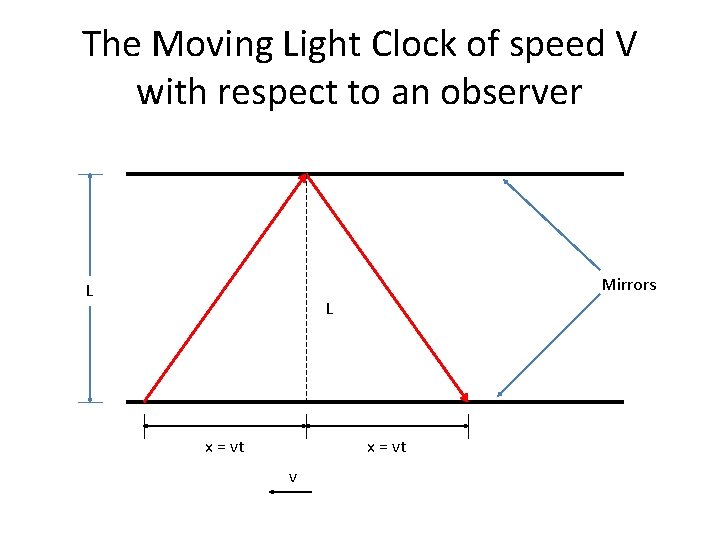
The Moving Light Clock of speed V with respect to an observer Mirrors L L x = vt v

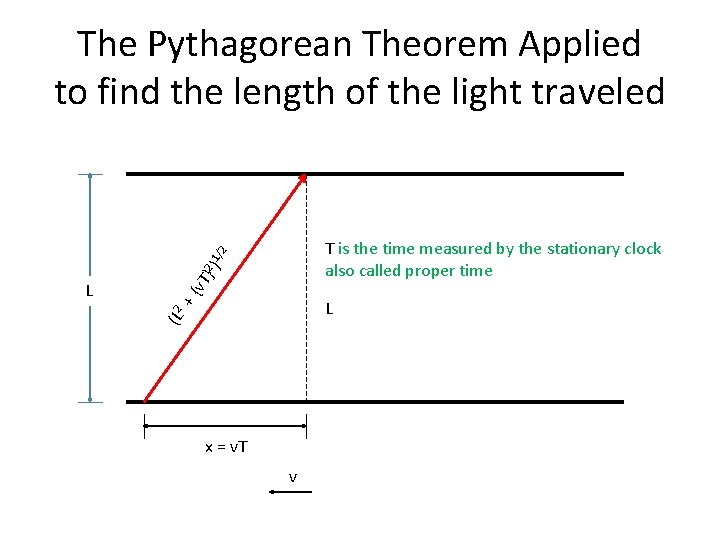
The Pythagorean Theorem Applied to find the length of the light traveled (L 2 + {v. T L } 2) 1 /2 T is the time measured by the stationary clock also called proper time L x = v. T v

Einstein’s Postulate The speed of light is constant in all reference frames • He came up with this postulate from the work of James Clerk Maxwell • Maxwell’s Equations came from the work of Michael Faraday • Michael Faraday performed experiments with electricity and magnetism and made many significant discoveries It was this postulate of Einstein’s that was a major key to solving the behavior of clocks in different reference frames

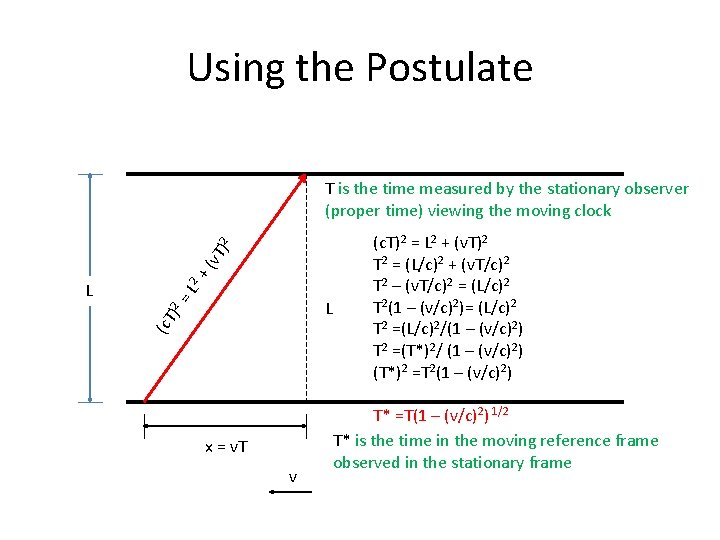
Using the Postulate L (c. T L ) 2 = L 2 + ( v. T )2 T is the time measured by the stationary observer (proper time) viewing the moving clock x = v. T v (c. T)2 = L 2 + (v. T)2 T 2 = (L/c)2 + (v. T/c)2 T 2 – (v. T/c)2 = (L/c)2 T 2(1 – (v/c)2)= (L/c)2 T 2 =(L/c)2/(1 – (v/c)2) T 2 =(T*)2/ (1 – (v/c)2) (T*)2 =T 2(1 – (v/c)2) T* =T(1 – (v/c)2) 1/2 T* is the time in the moving reference frame observed in the stationary frame

Time Dilation

Length Contraction We have seen that time can dilate. Let’s use some experimental observations. The muon ( a subatomic particle) has a rest (zero velocity) lifetime of 2. 2 microseconds before it disappears. These particles can be accelerated in a circular ring to near light speeds. Brookhaven National Laboratory has a machine that can accelerate muons to 99. 94% the speed of light in a circular ring with a diameter of 14 meters. This gives a circumference of 44 meters. The speed of light is 3 x 108 m/s. Taking the rest lifetime of 2. 2 x 10 -6 s (time observed by a stationary muon) times the speed of the muon gives the distance traveled. d = vt =. 9994(3 x 108 m/s)(2. 2 x 10 -6 s) = 660 m = 15 laps around the ring Experimental evidence shows a muon completes about 400 laps! What’s going on? !!!

Length Contraction (cont’d) Let’s calculate the time dilation according to Einstein: t = γt* t = 1/{(1 - (v/c)2)1/2 }t* t = 1/{(1 - (. 9994)2)1/2}(2. 2 x 10 -6 s) t = (28. 9)(2. 2 x 10 -6 s) t = 63 x 10 -6 s d = vt =. 9994(3 x 108 m/s)(63 x 10 -6 s) = 18888 m = 429 laps around the ring. Looks like Einstein is correct! So, the time dimension is deformable!

Length Contraction (cont’d) But, according to relativity, if you were riding a muon your clock would not be moving with respect to the muon so you and the muon would exist for 2. 2 microseconds. But, you and the muon did about 400 laps; that was measured. 400 laps in 2. 2 microseconds would imply a speed greater than the speed of light which is not plausible. The only thing left is to look at the distance you and the muon traveled. To be consistent, the circumference of the ring must have reduced by the same factor the lifetime increased! Let’s see: L = (1/γ)L* (L* is the rest length) L = (1/29)(44 m) L = 1. 51 m d =. 9994(3 x 108 m/s)(2. 2 x 10 -6 s) = 660 m/1. 51 m = 436 laps! So, length is deformable, and in this case is contracted for moving frames.

Time Is Not A Constant! Time is different in reference frames having different velocities • The basis is that the speed of light is constant in ALL reference frames • Time elapses slower in moving reference frames • The example showed the moving clock completes one tick in 1. 2 seconds when the stationary clock completes one tick in 1 second. • The time measurements are taken by the stationary clock (proper time). • The time for one tick of the moving clock observed in the moving frame is one 1 second! • moving clocks run “slow” compared to stationary clocks. • Satellite GPS systems must use this fact (satellites orbit the earth) so the satellite clocks agree with the earth clocks!

Length Is Not A Constant! Length is different in reference frames having different velocities • The basis is that the speed of light is constant in ALL reference frames • We showed length contraction with the muon experiment. The results of deformable time and length are part of Einstein’s Theory of Special Relativity He would formulate the Theory of General Relativity ten years later in 1915.

Spacetime We live in a spatial world of three dimensions • up-down • forwards-backwards • left-right We also live in a time world • the time elapsed between to events or a specific point in time So, we live in a Spacetime world! • Example: “I will see you at the mall (space coordinates) at 3 PM (time coordinate). ” This creates a Four Dimensional world with Spacetime coordinates of x, y, z, and t But remember, space and time are deformable and noticeably so at speeds nearing the speed of light.

Spacetime (cont’d) Three concepts are required to develop a Spacetime geometry (coordinate system). 1. Invariance –a law of nature that does not change when translated or rotated. • Example – a radio operates if it is moved (translation) and pointed in different directions (rotation). 2. Causality – cause and effect cannot be reversed. • Example – your mother caused your birth and there is nothing consistent with space or time that allows you to be born before your mother. 3. Distance – space is deformable and time is deformable but perhaps the two combined in a particular way is invariant.

Geometry We are familiar with Euclidian or flat geometry • The local area is treated as flat • The Pythagorean Theorem is shown to agree with measured results • The shortest distance between two points is a straight line • Parallel lines never intersect Other geometries can exist. One example: • Spherical geometry • The shortest distance between two points is a curve of minimum length on the surface of the sphere • Parallel lines intersect at the poles (lines of longitude all meet at the north and south pole)

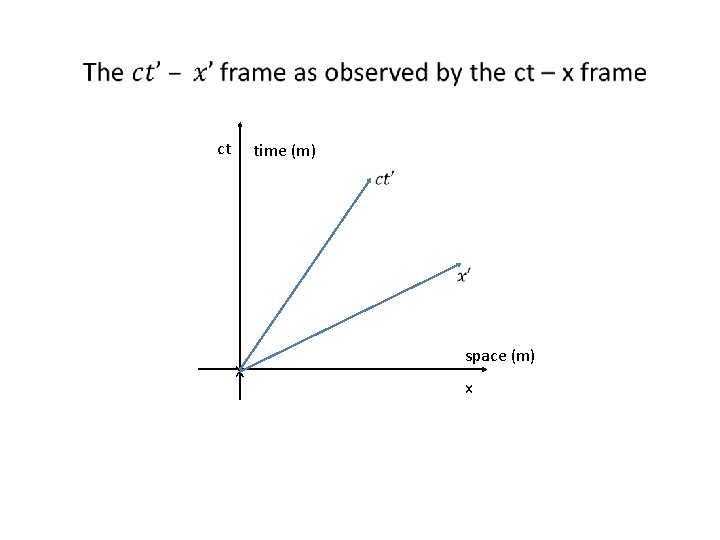
Spacetime Geometry The combination of the three spatial coordinates, x, y, and z and the time coordinate t. Example: I move from the living room to the kitchen • The distance can be measured with a ruler giving the distance in terms of x, y, and z coordinates • The time can be measured using a clock in the living room and one in the kitchen to determine the time elapses Remember: time and length are not absolute • Someone whizzing by will say your clock is running slow and the distance you traveled is less than what you measured. So, the big question is: • How do we establish an invariant distance in spacetime?

Spacetime Geometry Presently, the coordinate system we are using has units of meters (x, y, and z) and units of time (t) which are not compatible. However, we have heard of the light-year: the distance light travels in one year. This is a measure of distance in years, a unit of time. How do we express a distance in terms of time? v = x/t x = vt So, vt has units of distance. In general, let v = c, since c is the same in all reference frames. Now, compatible units can be used in the four dimensional spacetime coordinate system.

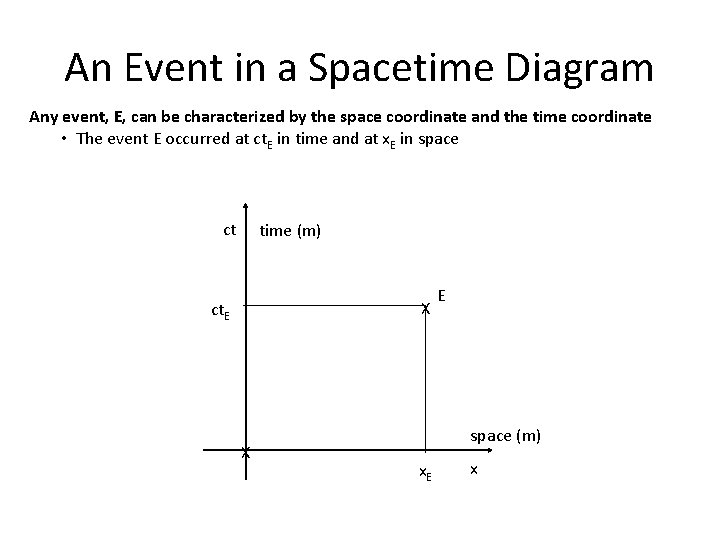
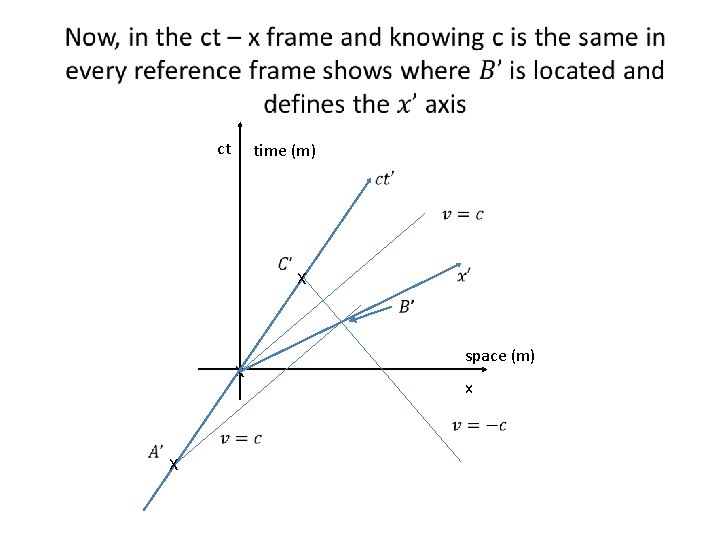
An Event in a Spacetime Diagram Any event, E, can be characterized by the space coordinate and the time coordinate • The event E occurred at ct. E in time and at x. E in space ct time (m) X ct. E X E space (m) x. E x

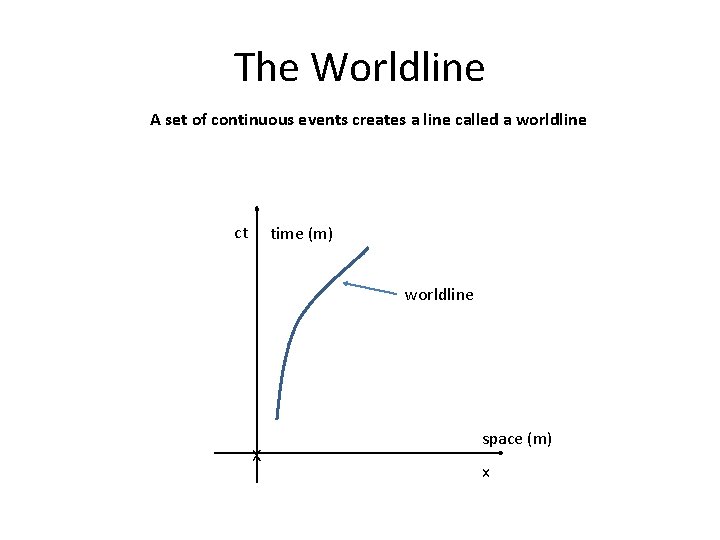
The Worldline A set of continuous events creates a line called a worldline ct time (m) worldline X space (m) x

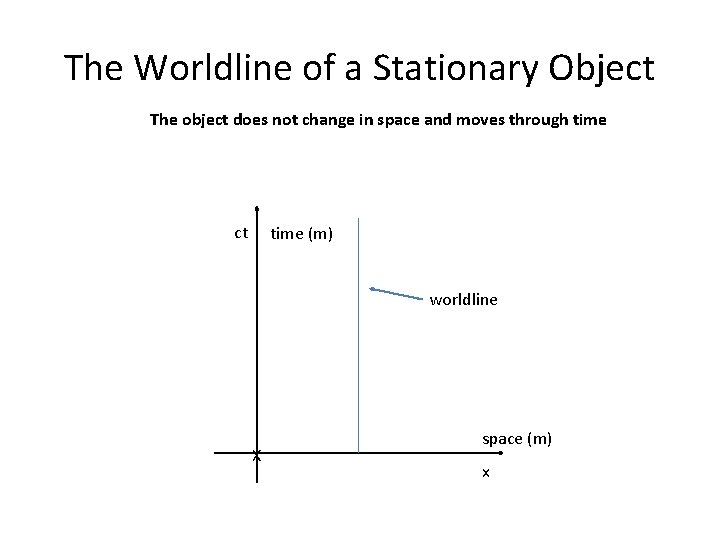
The Worldline of a Stationary Object The object does not change in space and moves through time ct time (m) worldline X space (m) x

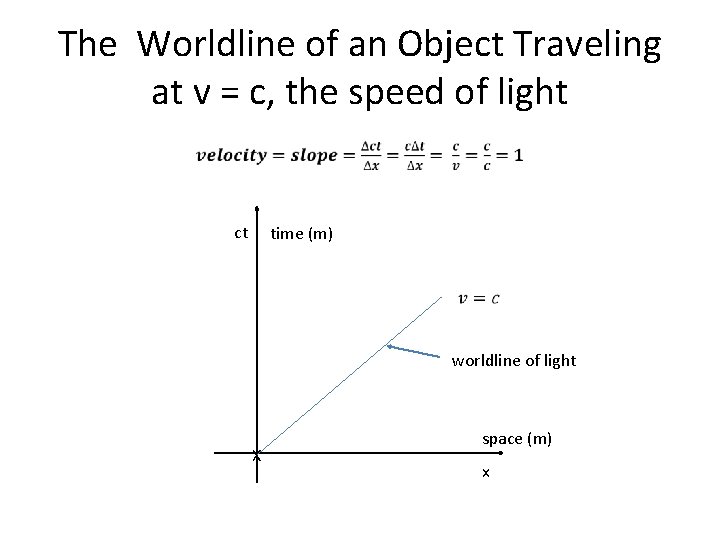
The Worldline of an Object Traveling at v = c, the speed of light ct time (m) worldline of light X space (m) x

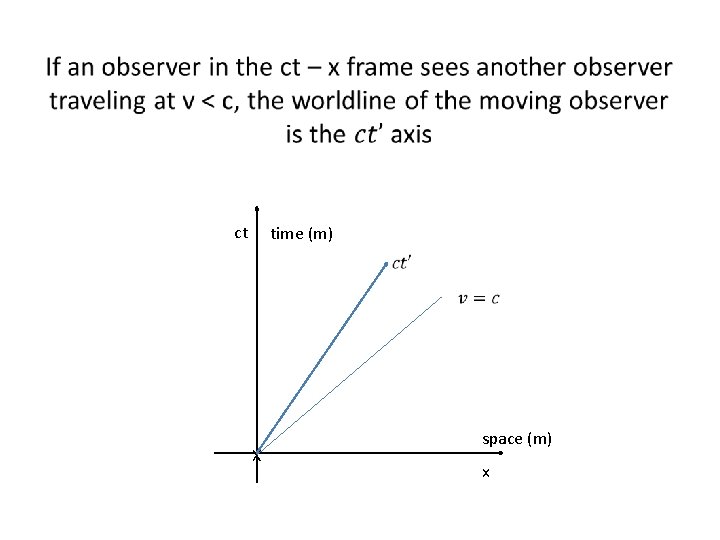
ct time (m) X space (m) x

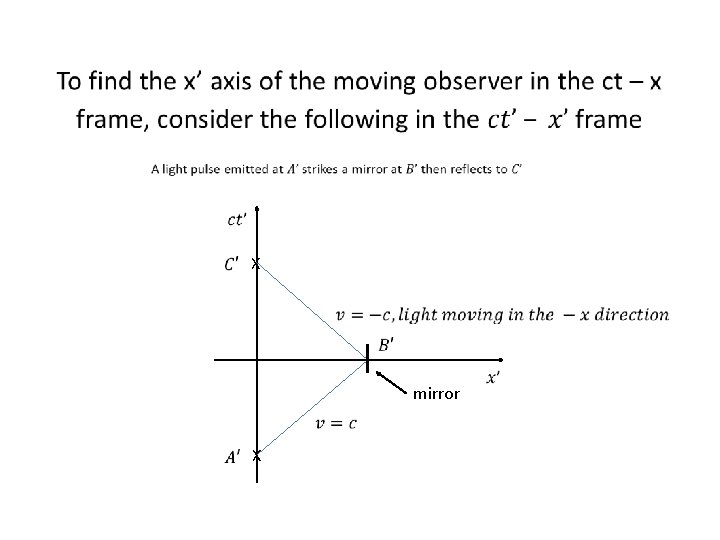
X mirror X

ct time (m) X space (m) X X x

ct time (m) X space (m) x

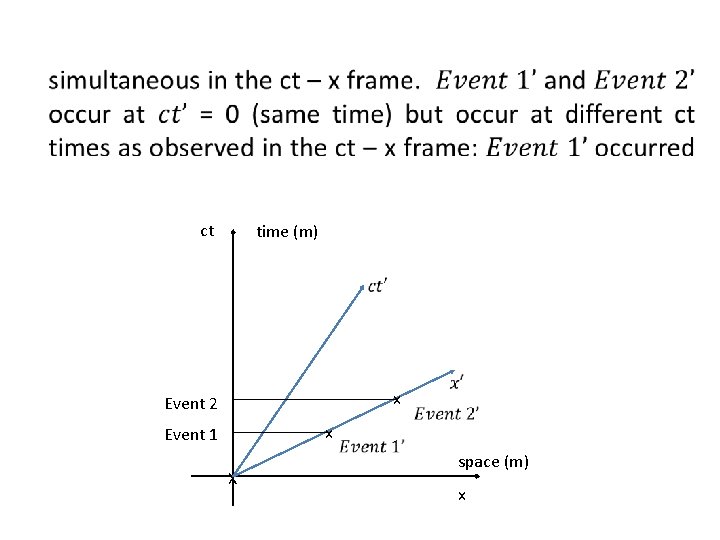
ct time (m) x Event 2 x Event 1 X space (m) x

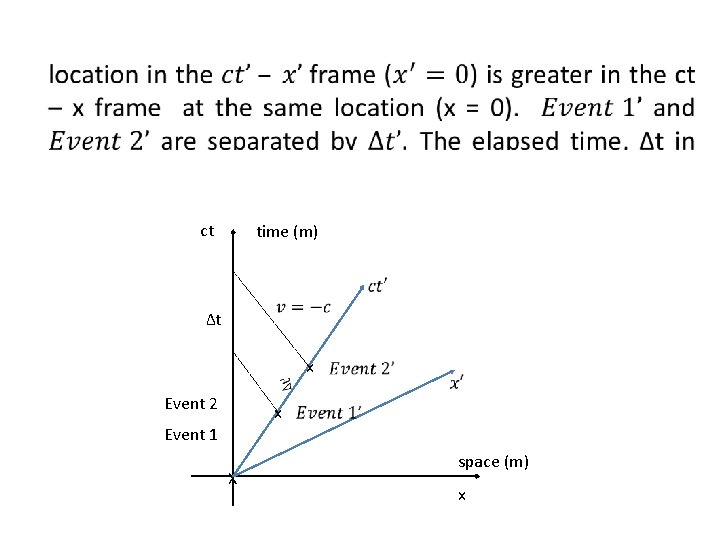
ct time (m) Δt x Event 2 x Event 1 X space (m) x

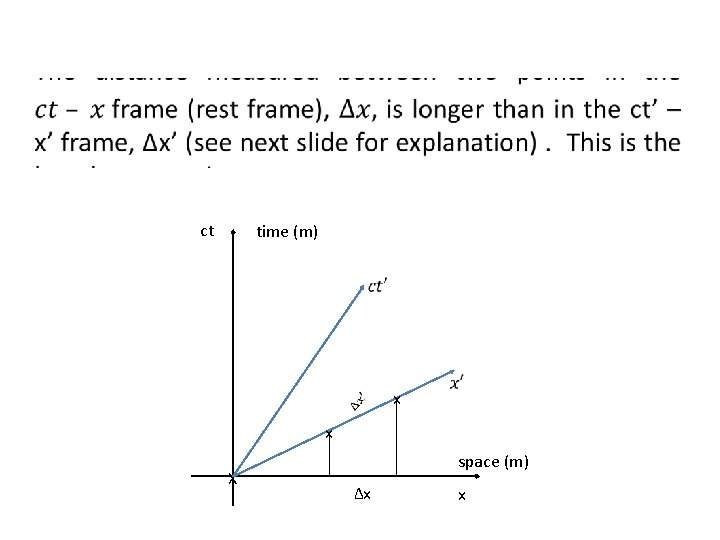
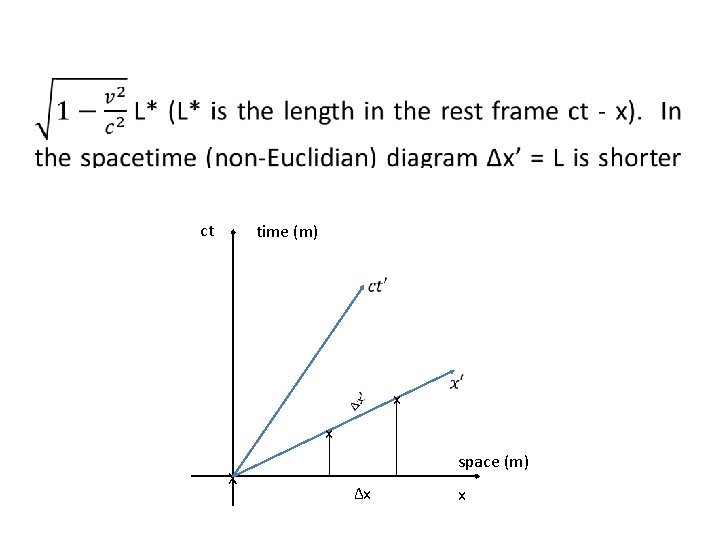
ct time (m) x x X space (m) Δx x

ct time (m) x x X space (m) Δx x

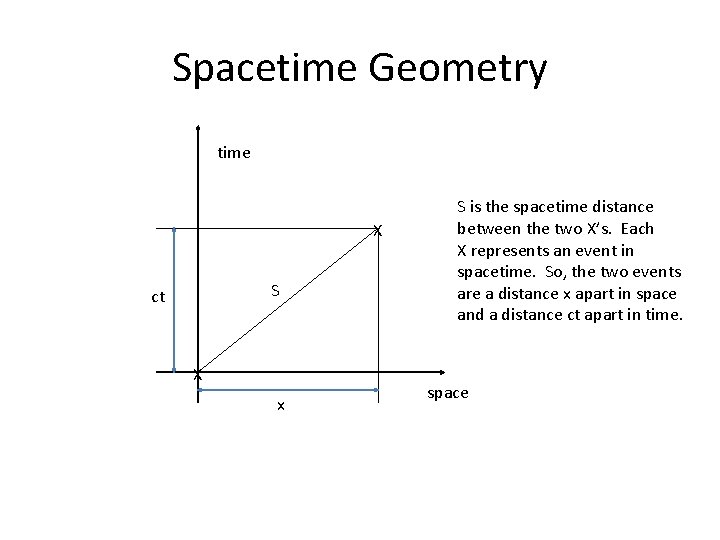
Spacetime Geometry time X S ct X x S is the spacetime distance between the two X’s. Each X represents an event in spacetime. So, the two events are a distance x apart in space and a distance ct apart in time. space

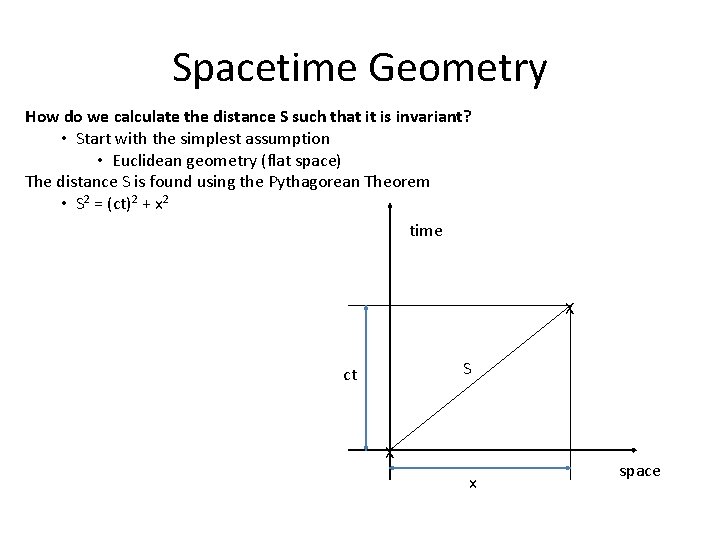
Spacetime Geometry How do we calculate the distance S such that it is invariant? • Start with the simplest assumption • Euclidean geometry (flat space) The distance S is found using the Pythagorean Theorem • S 2 = (ct)2 + x 2 time X S ct X x space

Euclidian Spacetime Geometry time X A A’ X S O X space X A’’ The Pythagorean Theorem applied here is the equation of a circle with radius S. Note that the space and time coordinates are different for different observers (someone whizzing by would measure a different x and t (A’ or A’’) compared to someone who is stationary (A)). If S is invariant with this geometry then every observer who is stationary, translating and/or rotating would agree the observed event lies on the circle.

Euclidian Spacetime Geometry time X A A’ X S O space X A’’ The events A and A’ have a positive time distance meaning the event O occurred Before A and A’. The event O took place before A or A’ and that is not a violation of causality. But, look at A’’. It has a negative time distance meaning A’’ happened before O; this is a violation of causality! Euclidian Spacetime violates Causality

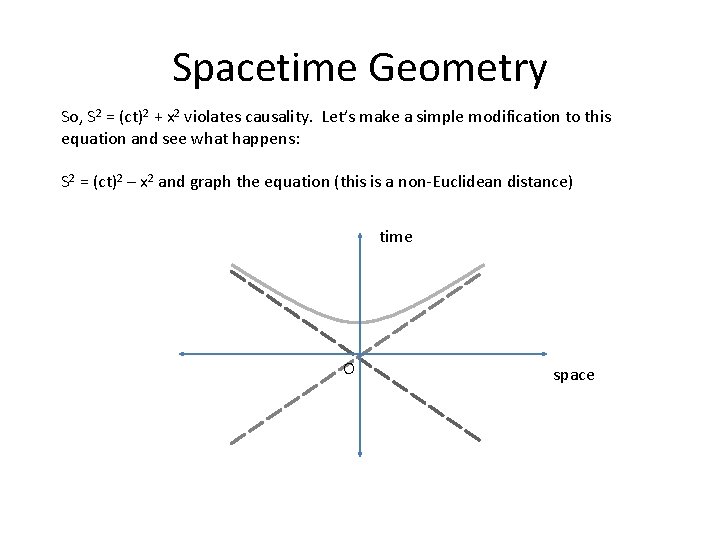
Spacetime Geometry So, S 2 = (ct)2 + x 2 violates causality. Let’s make a simple modification to this equation and see what happens: S 2 = (ct)2 – x 2 and graph the equation (this is a non-Euclidean distance) time O space

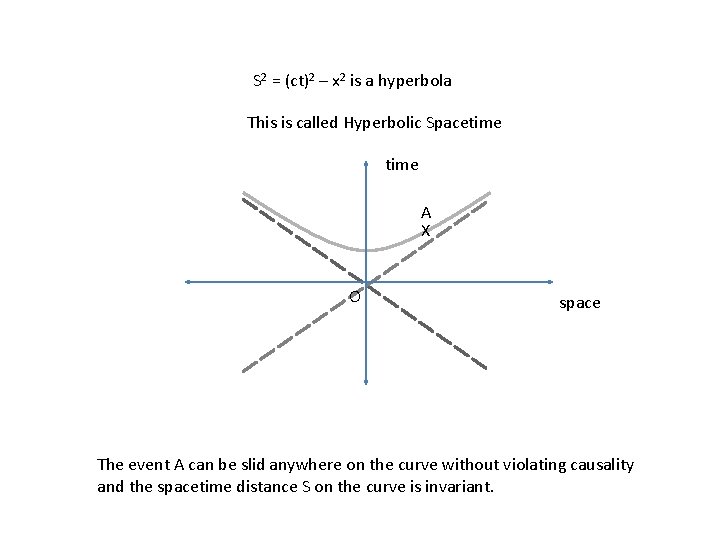
S 2 = (ct)2 – x 2 is a hyperbola This is called Hyperbolic Spacetime A X O space The event A can be slid anywhere on the curve without violating causality and the spacetime distance S on the curve is invariant.

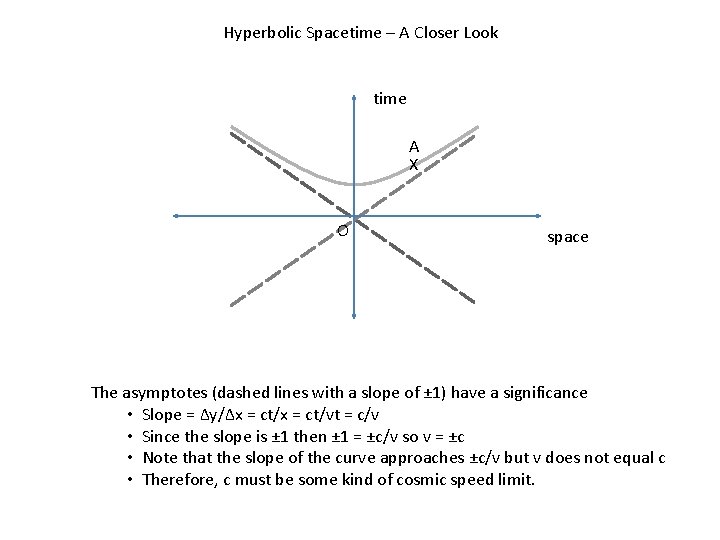
Hyperbolic Spacetime – A Closer Look time A X O space The asymptotes (dashed lines with a slope of ± 1) have a significance • Slope = Δy/Δx = ct/vt = c/v • Since the slope is ± 1 then ± 1 = ±c/v so v = ±c • Note that the slope of the curve approaches ±c/v but v does not equal c • Therefore, c must be some kind of cosmic speed limit.

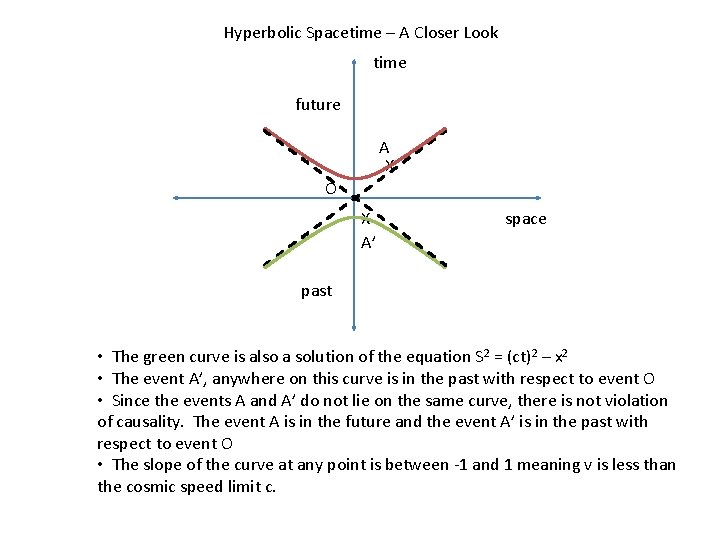
Hyperbolic Spacetime – A Closer Look time future A X O X A’ space past • The green curve is also a solution of the equation S 2 = (ct)2 – x 2 • The event A’, anywhere on this curve is in the past with respect to event O • Since the events A and A’ do not lie on the same curve, there is not violation of causality. The event A is in the future and the event A’ is in the past with respect to event O • The slope of the curve at any point is between -1 and 1 meaning v is less than the cosmic speed limit c.

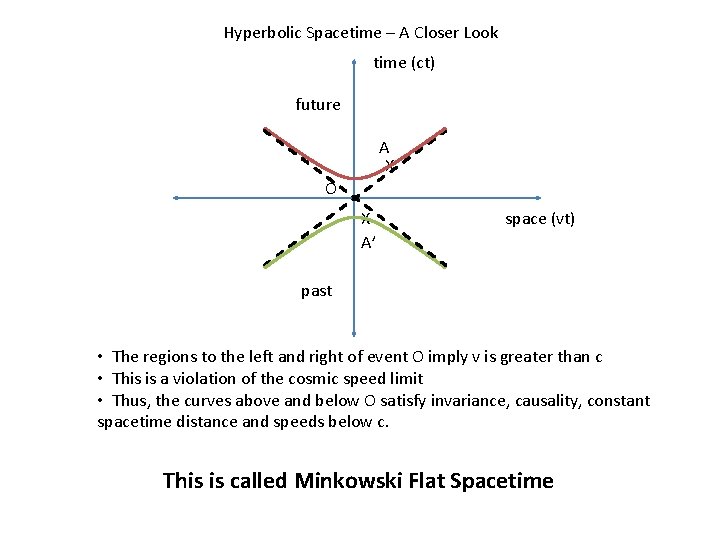
Hyperbolic Spacetime – A Closer Look time (ct) future A X O X A’ space (vt) past • The regions to the left and right of event O imply v is greater than c • This is a violation of the cosmic speed limit • Thus, the curves above and below O satisfy invariance, causality, constant spacetime distance and speeds below c. This is called Minkowski Flat Spacetime