The Flow Viz Menu and Parallel Scatterplot Matrix

The Flow. Viz. Menu and Parallel Scatterplot Matrix: Hybrid Multidimensional Visualizations for Network Exploration Christophe Viau, École de technologie supérieure, Montreal Michael J. Mc. Guffin, École de technologie supérieure, Montreal Yves Chiricota, Université du Québec à Chicoutimi, Chicoutimi Igor Jurisica, Ontario Cancer Institute, Toronto

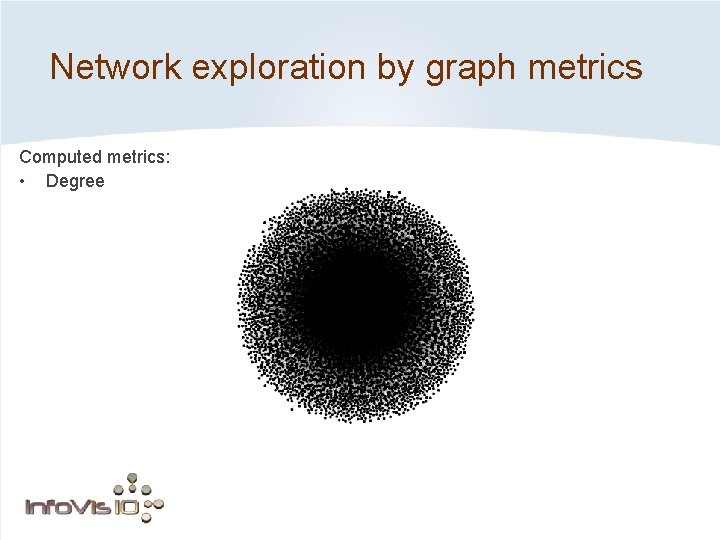
Network exploration by graph metrics ?

Network exploration by graph metrics Computed metrics: • Degree

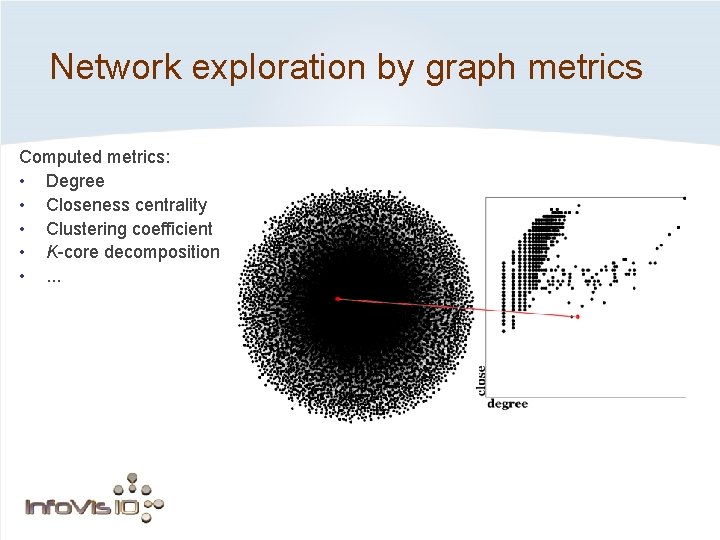
Network exploration by graph metrics Computed metrics: • Degree • Closeness centrality • Clustering coefficient • K-core decomposition • . . .

Network exploration by graph metrics Computed metrics: • Degree • Closeness centrality • Clustering coefficient • K-core decomposition • . . .

Multi-dimensional visualizations Scatterplot Matrix (SPLOM) Parallel Coordinates

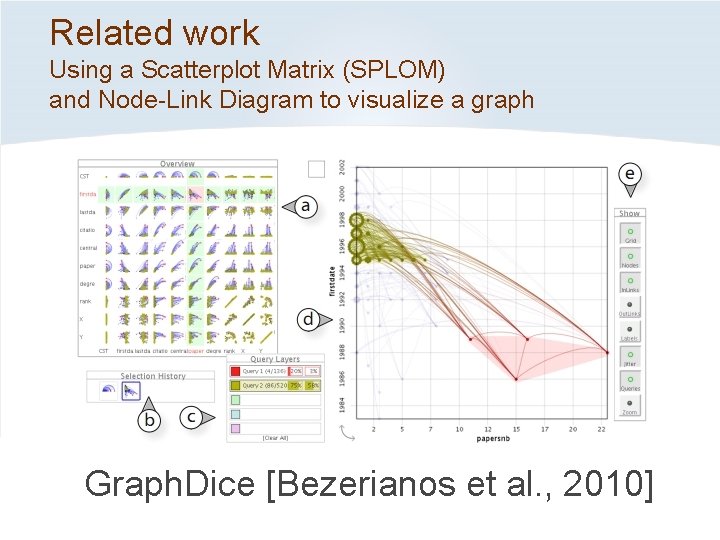
Related work Using a Scatterplot Matrix (SPLOM) and Node-Link Diagram to visualize a graph Graph. Dice [Bezerianos et al. , 2010]

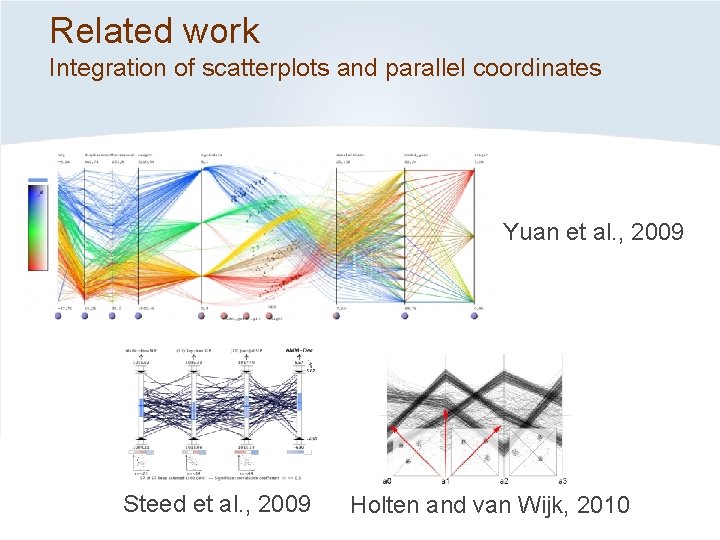
Related work Integration of scatterplots and parallel coordinates Yuan et al. , 2009 Steed et al. , 2009 Holten and van Wijk, 2010

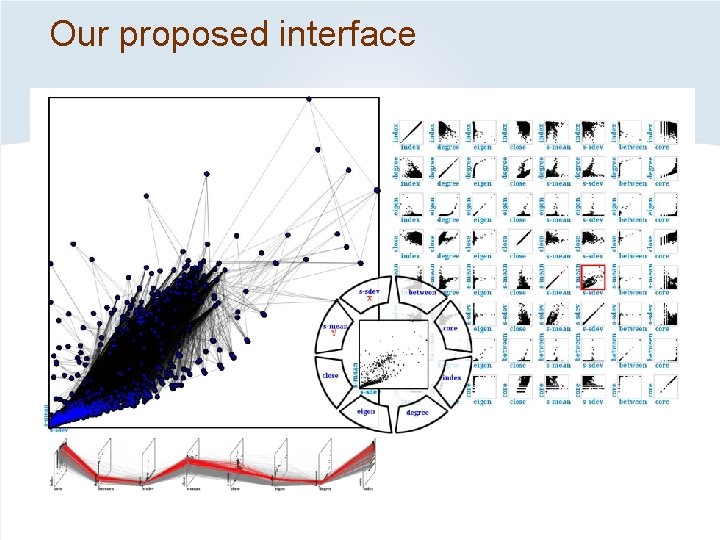
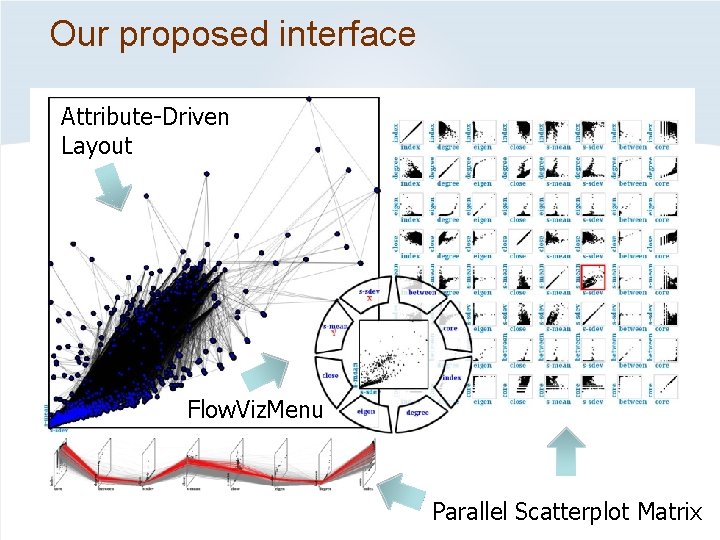
Our proposed interface

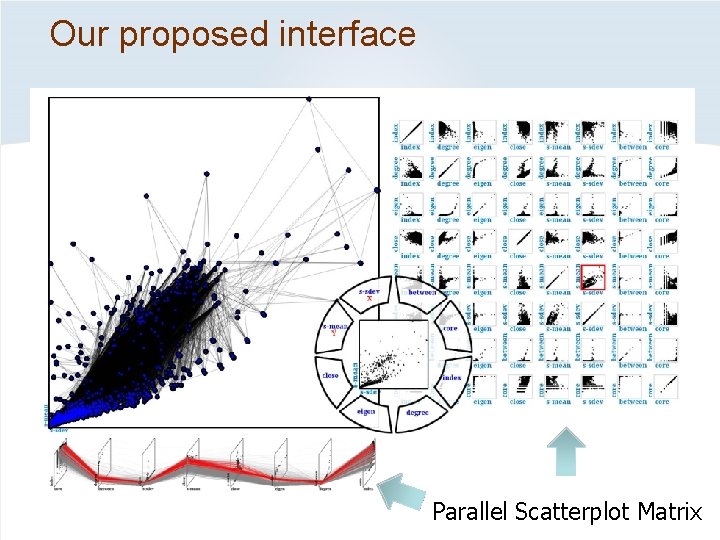
Our proposed interface Parallel Scatterplot Matrix

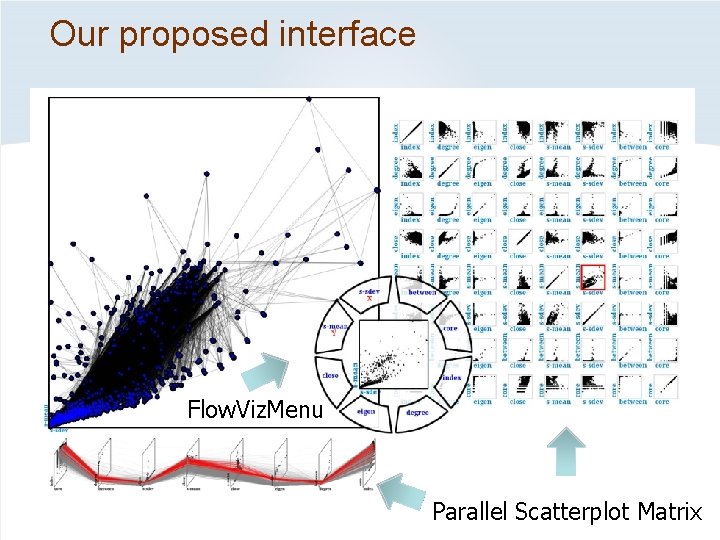
Our proposed interface Flow. Viz. Menu Parallel Scatterplot Matrix

Our proposed interface Attribute-Driven Layout Flow. Viz. Menu Parallel Scatterplot Matrix

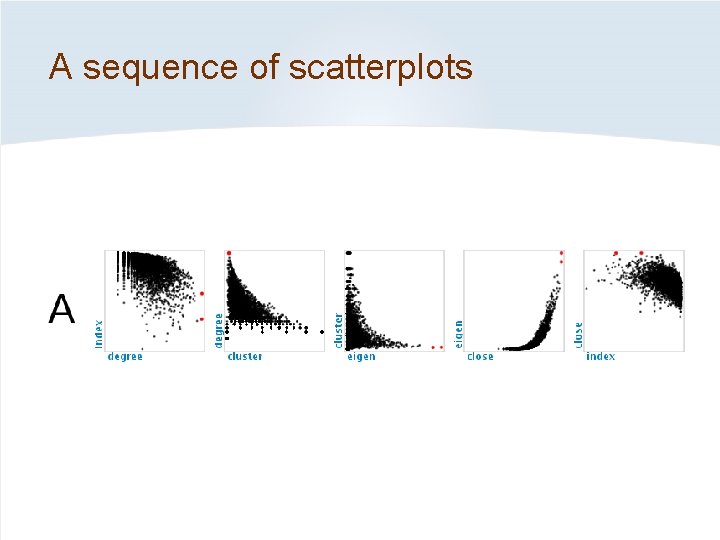
A sequence of scatterplots

A sequence of scatterplots

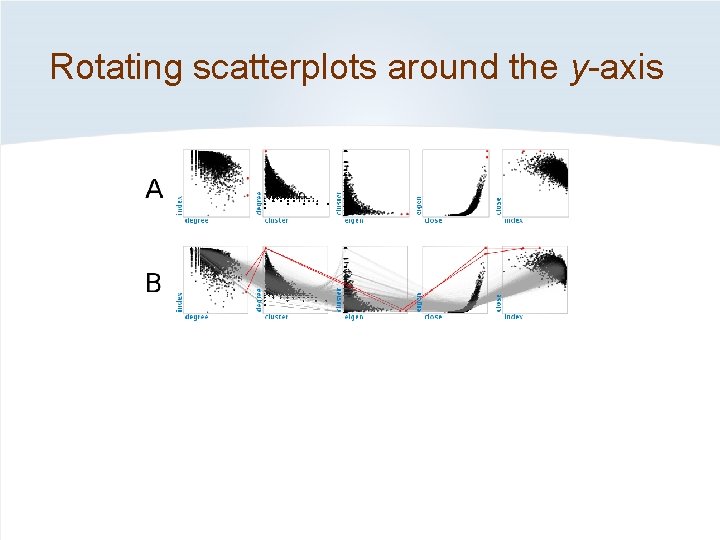
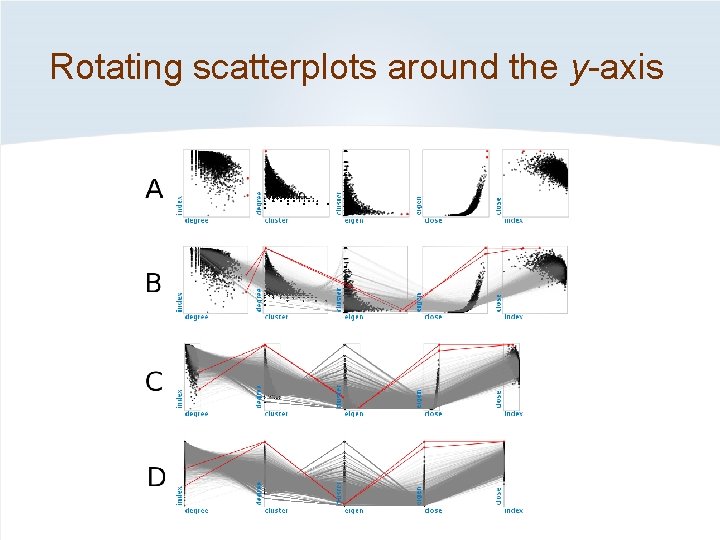
Rotating scatterplots around the y-axis

Rotating scatterplots around the y-axis

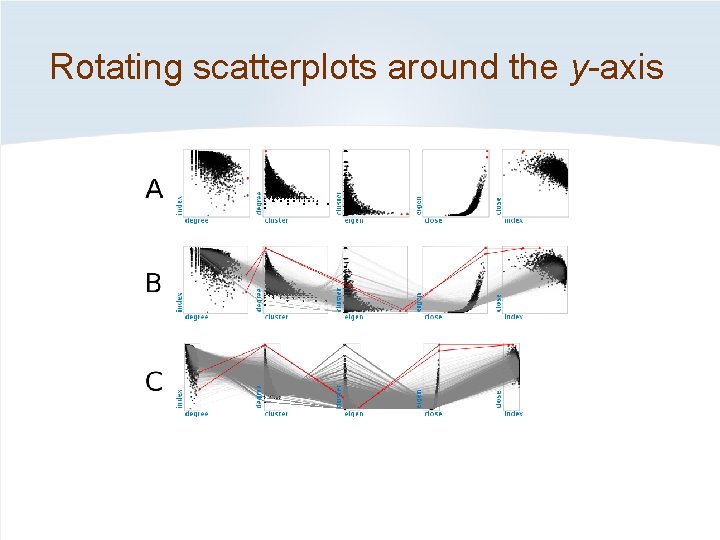
Rotating scatterplots around the y-axis

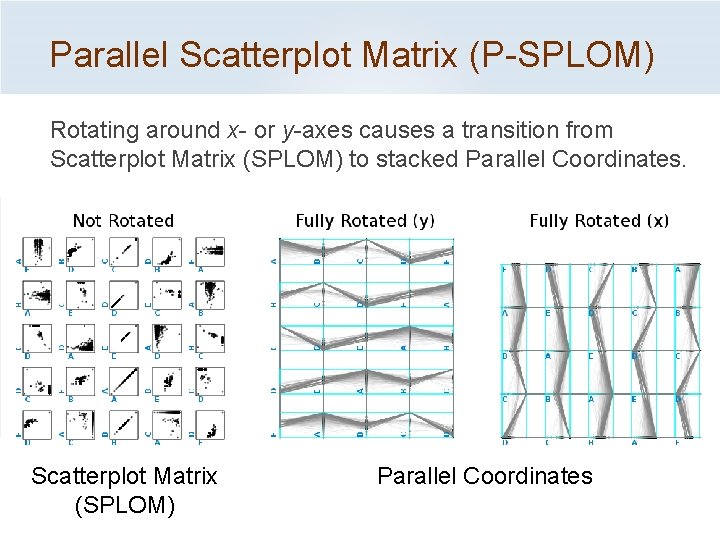
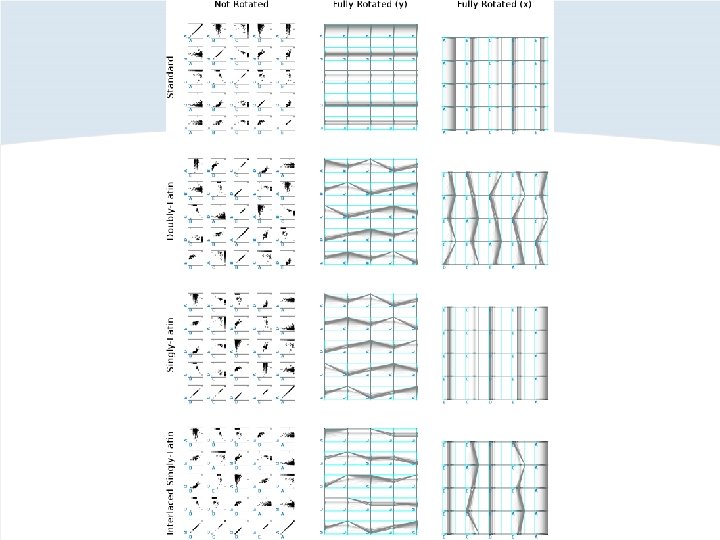
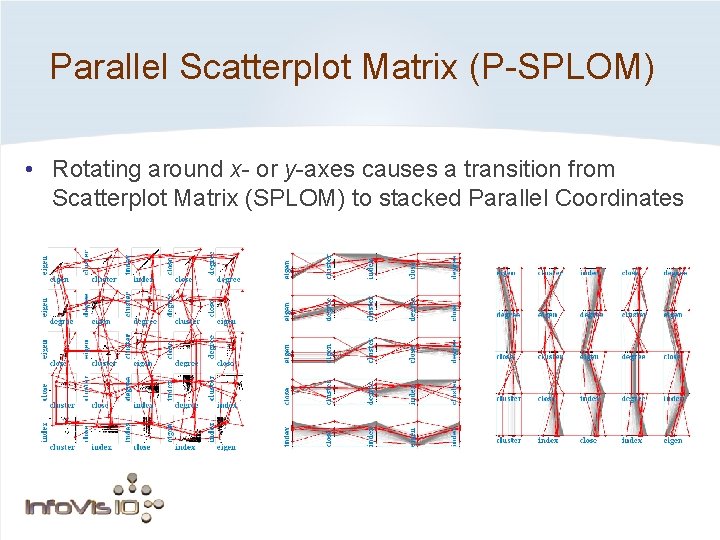
Parallel Scatterplot Matrix (P-SPLOM) Rotating around x- or y-axes causes a transition from Scatterplot Matrix (SPLOM) to stacked Parallel Coordinates. Scatterplot Matrix (SPLOM) Parallel Coordinates

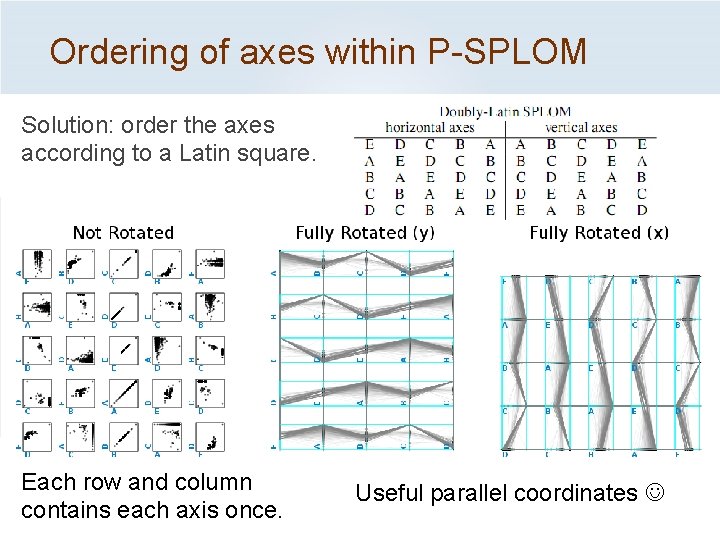
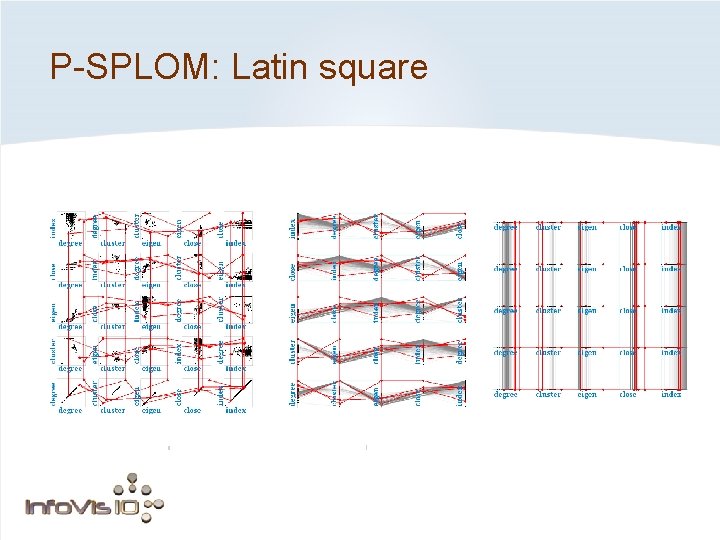
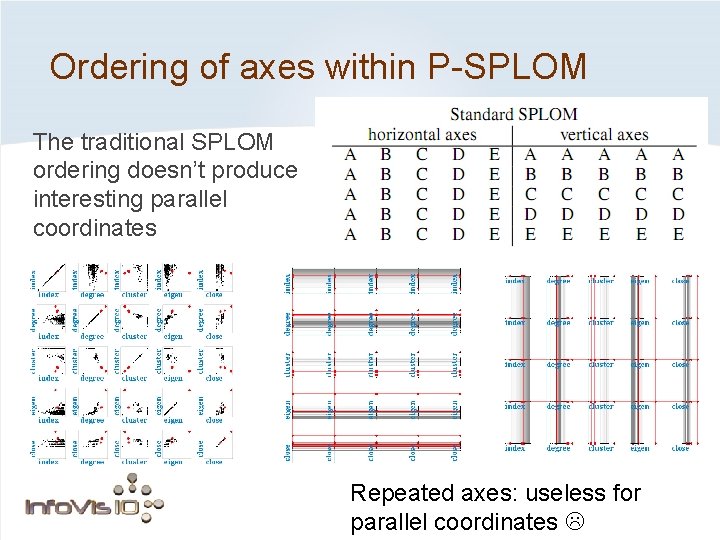
Ordering of axes within P-SPLOM Problem: traditional SPLOM ordering doesn’t yield useful parallel coordinates. Axes are repeated in each row and column Repeated axes: useless for parallel coordinates

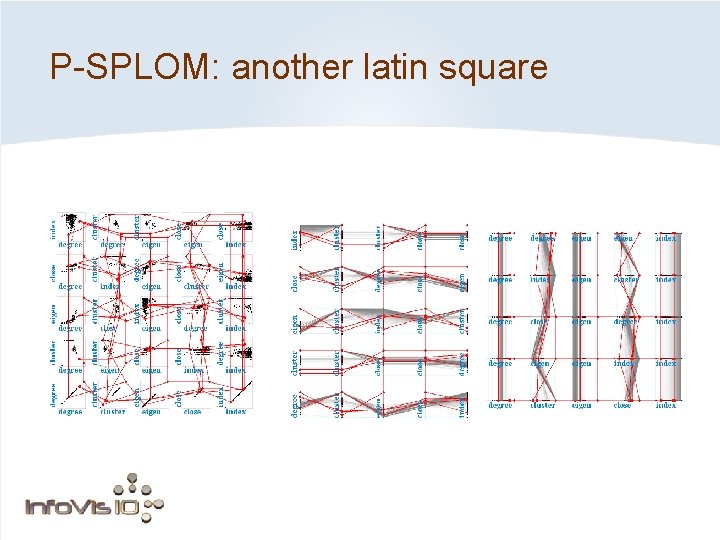
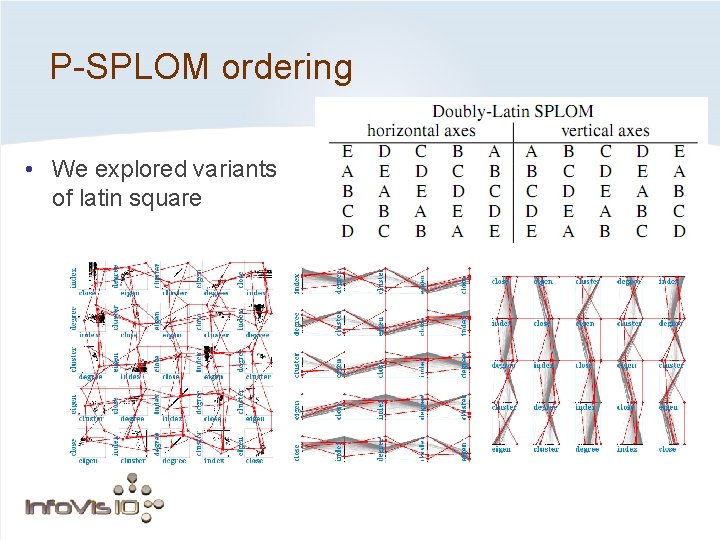
Ordering of axes within P-SPLOM Solution: order the axes according to a Latin square. Each row and column contains each axis once. Useful parallel coordinates

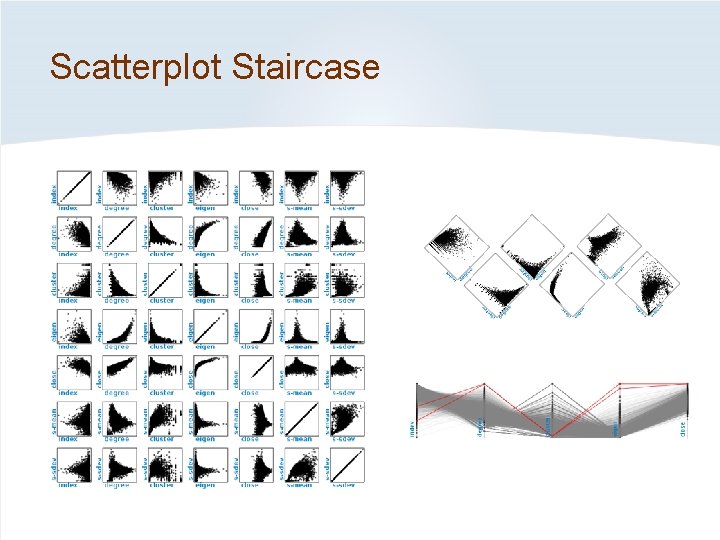
Scatterplot Staircase (SPLOS) Inspired partly by quilts [Watson et al. 2008] Sequence of scatterplots: treats one dimension differently. Scatterplot Staircase (SPLOS): all dimensions treated uniformly; every adjacent pair of plots share an axis. Parallel coordinates: more difficult to judge correlations than in scatterplots [Li et al. , 2010]

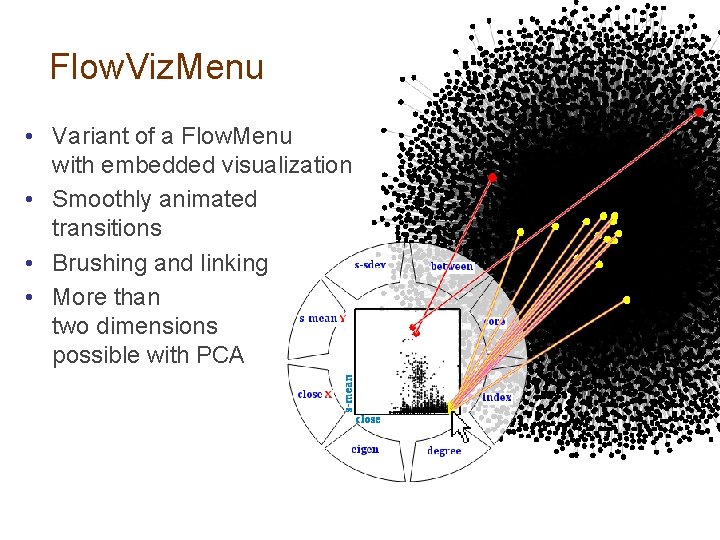
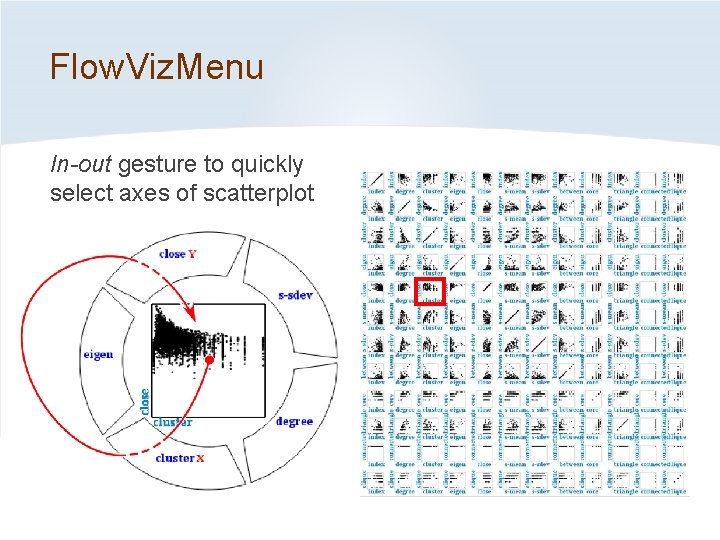
Flow. Viz. Menu • Variant of a Flow. Menu with embedded visualization • Smoothly animated transitions • Brushing and linking • More than two dimensions possible with PCA

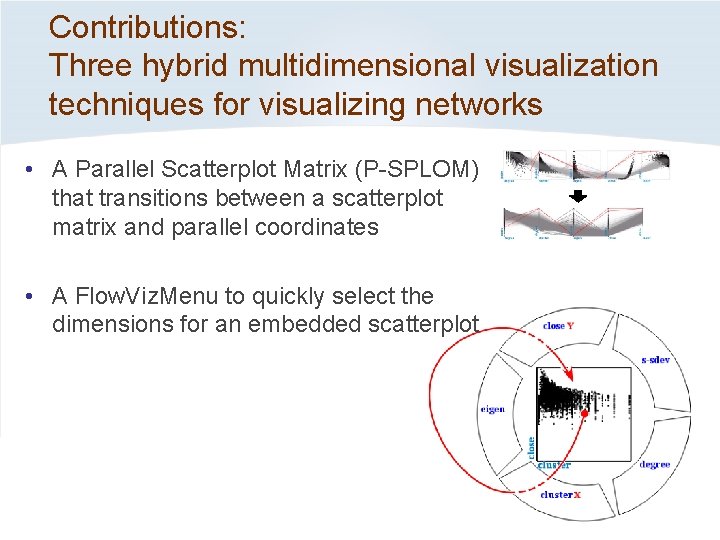
Flow. Viz. Menu In-out gesture to quickly select axes of scatterplot

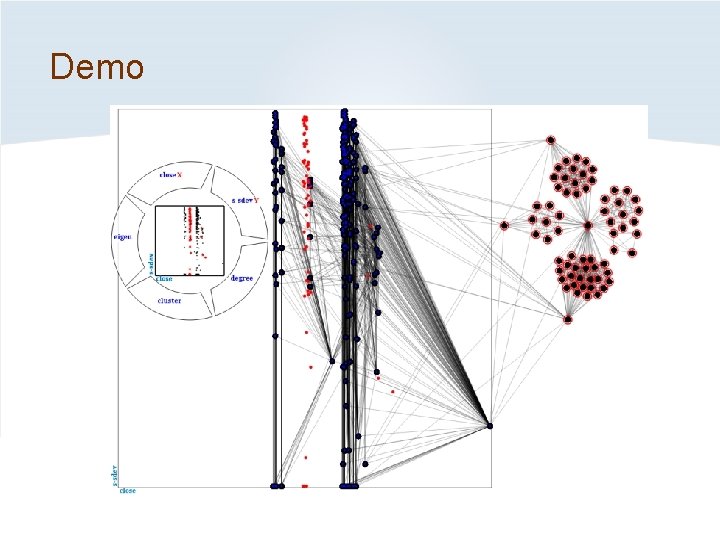
Attribute-Driven Layout (ADL) ADL: Layout based on a scatterplot selected in the Flow. Viz. Menu. The network layout can be a mixture of • Attribute-Driven Layout (ADL) • Manual layout • Force-directed layout

Demo

Initial user feedback Five bioinformaticians used our prototype and gave feedback. All had experience working with network data. Results: Pros: • Exploring along multiple metrics, smooth transitions, and integration of views were judged useful • All participants stated they would use the interface if it were made available to them Cons: • Some pairings of metrics within the scatterplots may not be useful • Too many hotkeys + button combinations in the current prototype

Contributions: Three hybrid multidimensional visualization techniques for visualizing networks

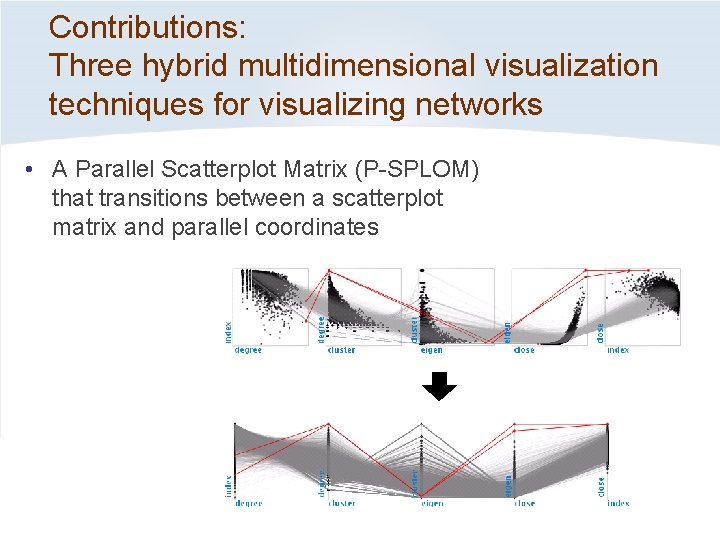
Contributions: Three hybrid multidimensional visualization techniques for visualizing networks • A Parallel Scatterplot Matrix (P-SPLOM) that transitions between a scatterplot matrix and parallel coordinates

Contributions: Three hybrid multidimensional visualization techniques for visualizing networks • A Parallel Scatterplot Matrix (P-SPLOM) that transitions between a scatterplot matrix and parallel coordinates

Contributions: Three hybrid multidimensional visualization techniques for visualizing networks • A Parallel Scatterplot Matrix (P-SPLOM) that transitions between a scatterplot matrix and parallel coordinates • A Flow. Viz. Menu to quickly select the dimensions for an embedded scatterplot

Contributions: Three hybrid multidimensional visualization techniques for visualizing networks • A Parallel Scatterplot Matrix (P-SPLOM) that transitions between a scatterplot matrix and parallel coordinates • A Flow. Viz. Menu to quickly select the dimensions for an embedded scatterplot

Contributions: Three hybrid multidimensional visualization techniques for visualizing networks • A Parallel Scatterplot Matrix (P-SPLOM) that transitions between a scatterplot matrix and parallel coordinates • A Flow. Viz. Menu to quickly select the dimensions for an embedded scatterplot • An Attribute-Driven Layout to configure the graph according to a scatterplot of graph metrics

Future directions • Application to other domains • Evaluation of performance and usability • Exploration of the design space of each visualization (e. g. , on a small screen)

Acknowledgments We thank our collaborators for their feedback: • SAP Business Objects • Members of Jurisica Lab at OCI • Members of the Multimedia Lab at ETS This research was funded by an SAP Business Objects ARC Fellowship, NSERC, and the FQRNT.

Thank you

P-SPLOM: variants

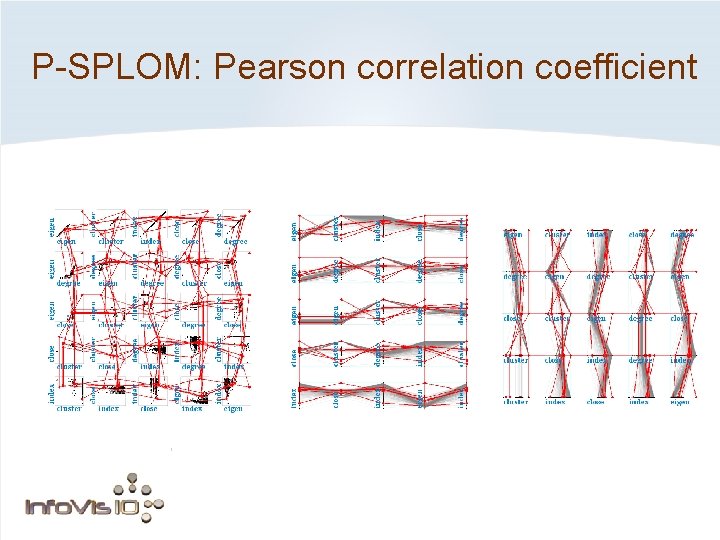
P-SPLOM: Pearson correlation coefficient

P-SPLOM: Latin square

P-SPLOM: another latin square

Scatterplot Staircase

Parallel Scatterplot Matrix (P-SPLOM) • Rotating around x- or y-axes causes a transition from Scatterplot Matrix (SPLOM) to stacked Parallel Coordinates

Ordering of axes within P-SPLOM The traditional SPLOM ordering doesn’t produce interesting parallel coordinates Repeated axes: useless for parallel coordinates

P-SPLOM ordering • We explored variants of latin square