The Fiedler Vector and Graph Partitioning Barbara Ball

The Fiedler Vector and Graph Partitioning Barbara Ball baljmb@aol. com Clare Rodgers clarerodgers@hotmail. com College of Charleston Graduate Math Department Research Under Dr. Amy Langville

Outline General Field of Data Clustering – – Motivation Importance Previous Work Laplacian Method Fiedler Vector Limitations Handling the Limitations

Outline Our Contributions – Experiments – – Sorting eigenvectors Testing Non-symmetric Matrices Hypotheses Implications Future Work – – Non-square matrices Proofs References

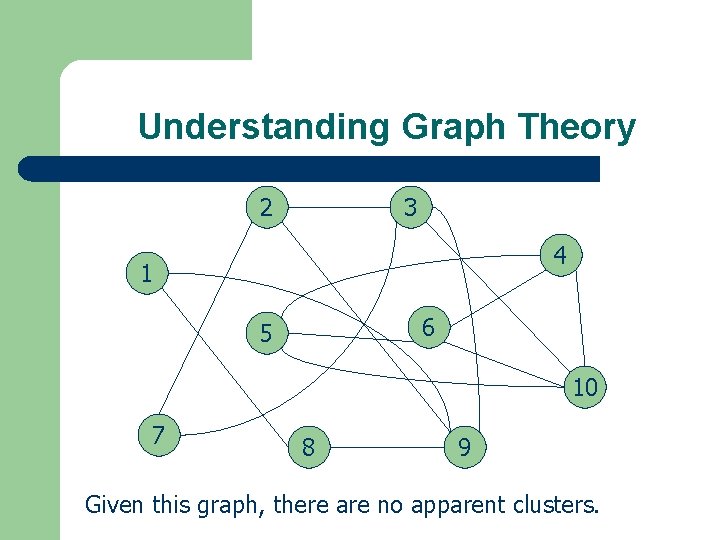
Understanding Graph Theory 2 3 4 1 6 5 10 7 8 9 Given this graph, there are no apparent clusters.

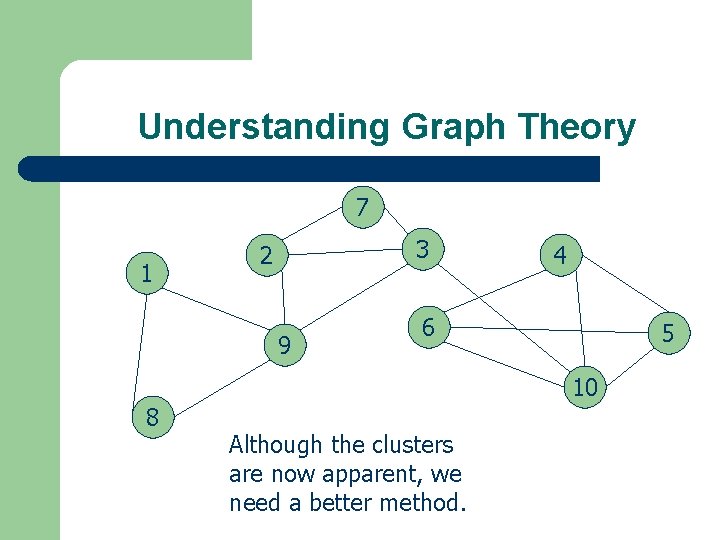
Understanding Graph Theory 7 1 3 2 9 4 6 5 10 8 Although the clusters are now apparent, we need a better method.

Finding the Laplacian Matrix • A = adjacency matrix Rows sum to zero • D = degree matrix • Find the Laplacian matrix, L • L=D-A 3 2 4 1 6 5 7 8 9 10

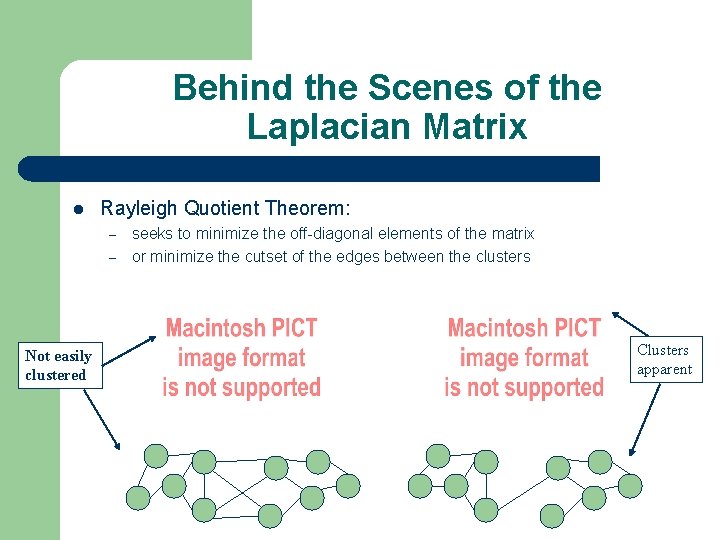
Behind the Scenes of the Laplacian Matrix Rayleigh Quotient Theorem: – – Not easily clustered seeks to minimize the off-diagonal elements of the matrix or minimize the cutset of the edges between the clusters Clusters apparent

Behind the Scenes of the Laplacian Matrix Rayleigh Quotient Theorem Solution: – – 1=0, the smallest right-hand eigenvalue of the symmetric matrix, L 1 corresponds to the trivial eigenvector v 1= e = [1, 1, …, 1]. Courant-Fischer Theorem: – also based on a symmetric matrix, L, searches for the eigenvector, v 2, that is furthest away from e.

Using the Laplacian Matrix v 2, gives relation information about the nodes. This relation is usually decided by separating the values across zero. A theoretical justification is given by Miroslav Fiedler. Hence, v 2 is called the Fiedler vector.

Using the Fiedler Vector v 2 is used to recursively partition the graph by separating the components into negative and positive values. Entire Graph: sign(V 2)=[-, -, -, +, +, +, -, -, -, +] Reds: sign(V 2)=[-, +, +, +, -, -] 1 2 3 7 8 1 8 4 9 7 2 9 6 3 5 10

Problems With Laplacian Method The Laplacian method requires the use of: – – – an undirected graph a structurally symmetric matrix square matrices Zero may not always be the best choice for partitioning the eigenvector values of v 2 (Gleich) Recursive algorithms are expensive

Current Clustering Method Monika Henzinger, Director of Google Research in 2003, cited generalizing directed graphs as one of the top six algorithmic challenges in web search engines.

How Are These Problems Currently Being Solved? Forcing symmetry for non-square matrices: – Suppose A is an (ad x term) non-square matrix. – B imposes symmetry on the information: Example:

How Are These Problems Currently Being Solved? Forcing symmetry in square matrices: – Suppose C represents a directed graph. – D imposes bidirectional information by finding the nearest symmetric matrix: D = C + CT Example:

How Are These Problems Currently Being Solved? Graphically Adding Data: 1 1 2 3

How Are These Problems Currently Being Solved? Graphically Deleting Data: 1 1 2 3

Our Wish: Use Markov Chains and the subdominant righthand eigenvector ( Ball-Rodgers vector) to cluster asymmetric matrices or directed graphs.

Where Did We Get the Idea? Stewart, in An Introduction to Numerical Solutions of Markov Chains, suggests the subdominant, right-hand eigenvector (Ball-Rodgers vector) may indicate clustering.

The Markov Method

Different Matrices and Eigenvectors Different Matrices: A: connectivity matrix Respective Eigenvectors: L = D – A : Laplacian matrix – P: probability Markov matrix – rows sum to 0 – 2 nd smallest of L (Fiedler vector) 2 nd largest of P (Ball-Rodgers vector) 2 nd smallest of Q the rows sum to 1 Q = I – P: transitional rate matrix rows sum to 0 2 nd largest of A 2 nd smallest of A

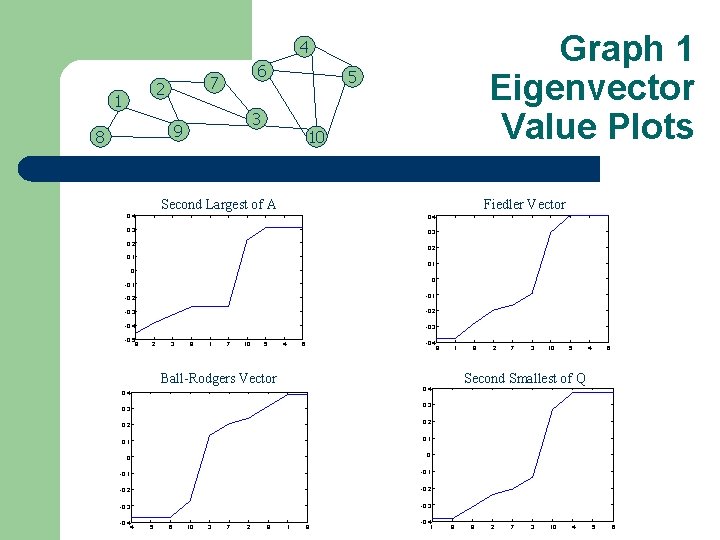
Graph 1 Eigenvector Value Plots 4 2 1 6 7 3 9 8 5 10 Second Largest of A Fiedler Vector 0. 4 0. 3 0. 2 0. 1 0 0 -0. 1 -0. 2 -0. 1 -0. 3 -0. 2 -0. 4 -0. 3 -0. 5 9 2 3 8 1 7 10 5 4 -0. 4 6 Ball-Rodgers Vector 1 9 2 7 3 10 5 4 6 Second Smallest of Q 0. 4 0. 3 0. 2 0. 1 0 0 -0. 1 -0. 2 -0. 3 -0. 4 8 4 5 6 10 3 7 2 9 1 8 -0. 4 1 8 9 2 7 3 10 4 5 6

4 1 8 7 2 9 6 3 5 10 Graph 1 Banding Using Eigenvector Values Banded A Banded P Banded L Reorders just by using the indices of the sorted eigenvector – No Recursion Banded Q

4 1 8 7 2 9 A 6 3 5 10 Graph 1 Reordering Using Laplacian Method Reordered L

4 1 7 2 9 8 6 3 5 10 A Graph 1 Reordering Using Markov Method Reordered P Reordered Q

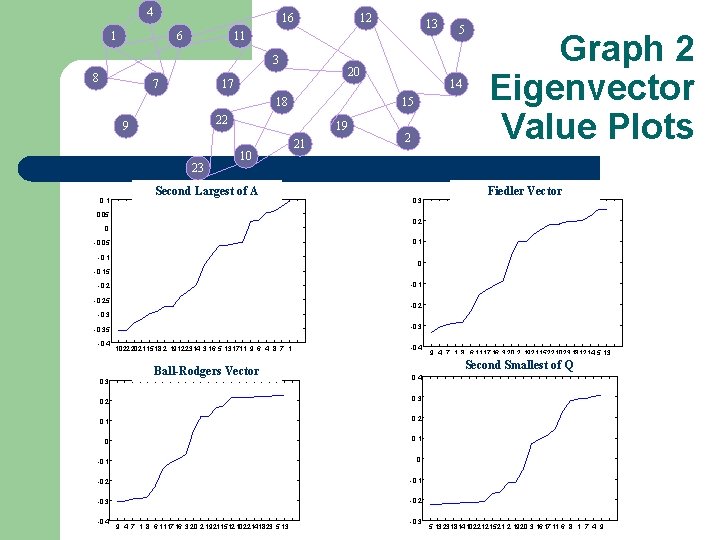
4 16 1 6 12 3 8 7 20 17 18 23 19 10 Second Largest of A 0. 05 21 5 14 15 22 9 0. 1 13 11 2 0. 3 Graph 2 Eigenvector Value Plots Fiedler Vector 0. 2 0 0. 1 -0. 05 -0. 1 0 -0. 15 -0. 1 -0. 25 -0. 2 -0. 35 -0. 4 0. 3 1022 2021 1518 2 19122314 3 16 5 131711 9 6 4 8 7 1 Ball-Rodgers Vector -0. 4 Second Smallest of Q 0. 4 0. 2 0. 3 0. 1 0. 2 0 0. 1 -0. 1 0 -0. 2 -0. 1 -0. 3 -0. 2 -0. 4 9 4 7 1 8 6 1117 16 3 20 2 192115121022141823 5 13 9 4 7 1 8 6 1117 16 3 20 2 19211522 1023 181214 5 13 -0. 3 5 13231814102212 1521 2 1920 3 161711 6 8 1 7 4 9

4 16 1 6 12 3 8 13 11 7 20 17 18 23 19 10 21 Graph 2 Banding Using Eigenvector Values 14 15 22 9 5 2 Banded A Banded L Nicely banded, but no apparent blocks. Banded P Banded Q

4 16 1 6 12 3 8 13 11 7 20 17 18 23 19 21 10 14 15 22 9 5 2 Graph 2 Reordering Using Laplacian Method Reordered L A

4 16 1 6 12 3 8 13 11 7 20 17 18 23 19 10 14 15 22 9 21 5 2 Graph 2 Reordering Using Markov Method Reordered P A Reordered Q

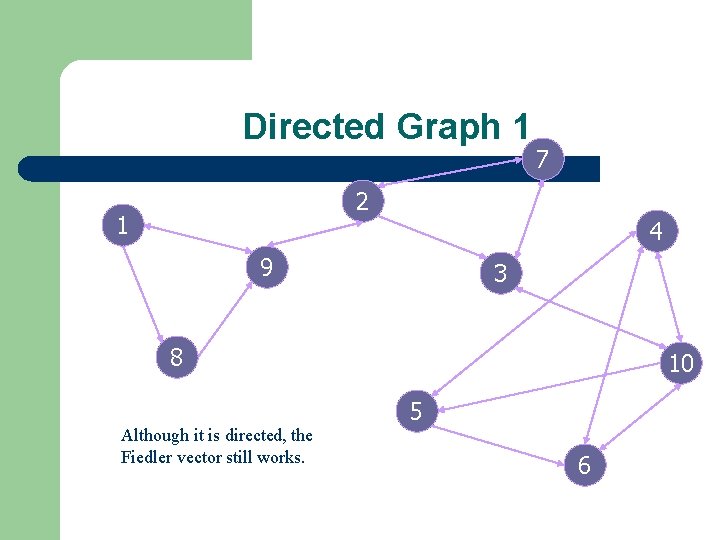
Directed Graph 1 7 2 1 4 9 3 8 Although it is directed, the Fiedler vector still works. 10 5 6

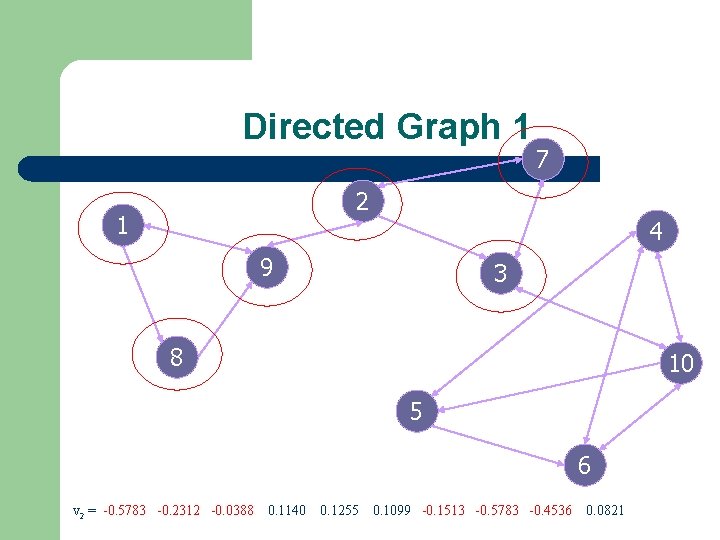
Directed Graph 1 7 2 1 4 9 3 8 10 5 6 v 2 = -0. 5783 -0. 2312 -0. 0388 0. 1140 0. 1255 0. 1099 -0. 1513 -0. 5783 -0. 4536 0. 0821

7 2 3 1 9 4 10 Directed Graph 1 Reordering Using Laplacian Method 8 5 6 Reordered L A

7 2 3 1 9 4 10 Directed Graph 1 Reordering Using Markov Method 8 5 6 A Reordered P

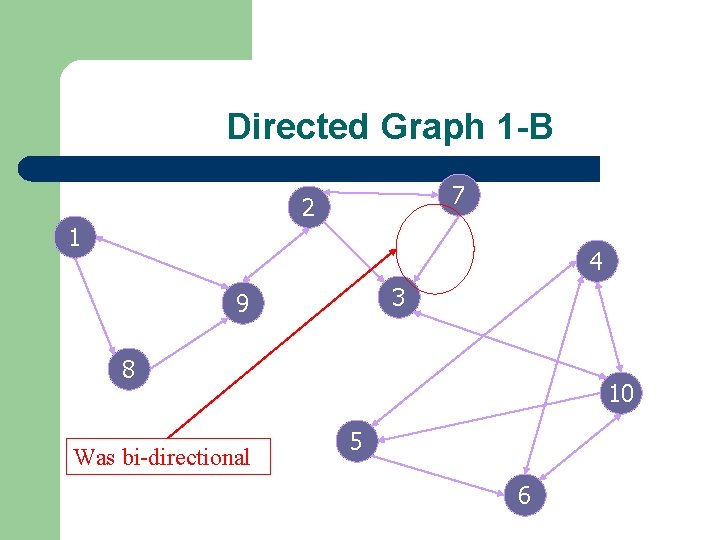
Directed Graph 1 -B 7 2 1 4 3 9 8 Was bi-directional 10 5 6

Directed Graph 1 -B The Laplacian Method no longer works on this graph. Certain edges must be bi-directional in order to make the matrix irreducible. 7 Currently, to deal with 2 3 this problem, a small 1 number is added to each 9 4 10 element of the matrix. . 01 8 5 6

7 2 3 4 1 10 9 5 6 8 A Directed Graph 1 -B Reordering Using Markov Method Reordered P

Answer Directed Graph 2 Reordering Using Markov Method Reordered P A

Answer Directed Graph 3 Reordering Using Markov Method Reordered P A

Answer Directed Graph 4 Reordering Using Markov Method 10% antiblock elements A Reordered P

Answer Directed Graph 5 Reordering Using Markovian Method 30% antiblock elements A Only the first partition is shown. Reordered P

Hypothesis Implications Plotting the eigenvector values gives better estimates of the number of clusters A number other than zero may be used to partition the eigenvector values. Sometimes, sorting the eigenvector values clusters the matrix without any type of recursive process. Recursive methods are timeconsuming. The eigenvector plot takes virtually no time at all and requires very little programming or storage! Using the stochastic matrix P cluster asymmetric matrices or directed graphs Non-symmetric matrices (or directed graphs) can be clustered without altering data!

Future Work Experiments on Large Non-Symmetric Matrices Non-square matrices Clustering eigenvector values to avoid recursive programming Proofs Questions

References Friedberg, S. , Insel, A. , and Spence, L. Linear Algebra: Fourth Edition. Prentice-Hall. Upper Saddle River, New Jersey, 2003. Gleich, David. Spectral Graph Partitioning and the Laplacian with Matlab. January 16, 2006. http: //www. stanford. edu/~dgleich/demos/matlab/spectral. html Godsil, Chris and Royle, Gordon. Algebraic Graph Theory. Springer-Verlag New York, Inc. New York. 2001. Karypis, George. http: //glaros. dtc. umn. edu/gkhome/node Langville, Amy. The Linear Algebra Behind Search Engines. The Mathematical Association of America – Online. http: //www. joma. org. December, 2005. Mark S. Aldenderfer, Mark S. and Roger K. Blashfield. Cluster Analysis. Sage University Paper Series: Quantitative Applications in the Social Sciences, 1984. Moler, Cleve B. Numerical Computing with MATLAB. The Society for Industrial and Applied Mathematics. Philadelphia, 2004. Roiger, Richard J. and Michael W. Geatz. Data Mining: A Tutorial-Based Primer Addison-Wesley, 2003. Vanscellaro, Jessica E. “The Next Big Thing In Searching” Wall Street Journal. January 24, 2006.

References Zhukov, Leonid. Technical Report: Spectral Clustering of Large Advertiser Datasets Part I. April 10, 2003. Learning MATLAB 7. 2005. www. mathworks. com www. Mathworld. com www. en. wikipedia. org/ http: //www. resample. com/xlminer/help/HClst_intro. htm http: //comp 9. psych. cornell. edu/Darlington/factor. htm www-groups. dcs. st-and. ac. uk/~history/Mathematicians/Markov. html http: //leto. cs. uiuc. edu/~spiros/publications/ACMSRC. pdf http: //www. lifl. fr/~iri-bn/talks/SIG/higham. pdf http: //www. epcc. ed. ac. uk/computing/training/document_archive/meshdecompslides/Mesh. Decomp-70. html http: //www. cs. berkeley. edu/~demmel/cs 267/lecture 20. html http: //www. maths. strath. ac. uk/~aas 96106/rep 02_2004. pdf

Eigenvector Example back

Structurally Symmetric back

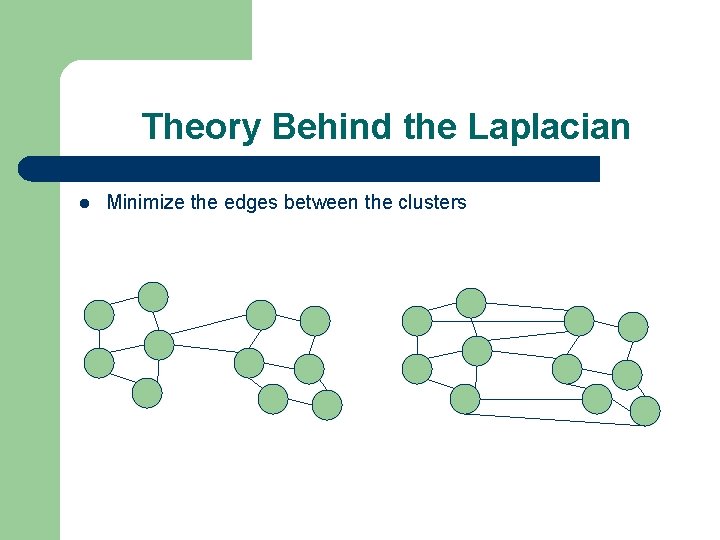
Theory Behind the Laplacian Minimize the edges between the clusters

Theory Behind the Laplacian Minimizing edges between clusters is the same as minimizing off-diagonal elements in the Laplacian matrix. min p. TLp where pi = {-1, 1} and i is the each node. p represents the separation of the nodes into positives and negatives. p. TLp = p. T(D-A)p = p. TDp – p. TAp However, p. TDp is the sum across the diagonal, so is is a constant. Constants do not change the outcome of optimization problems.

Theory Behind the Laplacian min p. TAp This is an integer nonlinear program. This can be changed to a continuous program by using Lagrange relaxation and allowing p to take any value from – 1 to 1. We rename this vector x, and let its magnitude be N. So, x. Tx=N. min x. TAx - (x. Tx – N) This can be rewritten as the Rayleigh Quotient: min x. TAx/x. Tx = 1

Theory Behind the Laplacian 1=0 and corresponds to the trivial eigenvector v 1=e The Courant-Fischer Theorem seeks to find the next best solution by adding an extra constraint of x e. This is found to be the subdominant eigenvector v 2, known as the Fiedler vector.

Theory Behind the Laplacian Our Questions: – The symmetry requirement is needed for the matrix diagonalization of D. Why is D important since it is irrelevant for a minimization problem? – If diagonalization is important, could SVD be used instead? future