The Exponential Distribution Continuous Random Variables 1 Some

The Exponential Distribution Continuous Random Variables 1

Some Special Continuous Distributions � We do not often deal with General CRVs but rather special cases � Some ◦ ◦ ◦ important distributions you may see are: Uniform Exponential Gamma/Erlang Normal Chi-squared 2

Comparing Distributions � In a previous example the Poisson distribution defined a random variable as the number of flaws along a length of wire (flaws per mm). � The exponential distribution defines a random variable as the interval between flaws (mm’s between flaws – the inverse). 3

Exponential Distribution random variable X that equals the distance between successive events of a Poisson process with mean number of events λ > 0 per unit interval is an exponential random variable with parameter λ. � The f(x) = λe-λx and F(x) = 1 – e-λx � Measures: 4

Exponential Distribution graph � The y-intercept of the exponential probability density function is λ. � The random variable is non-negative and extends to infinity. 5

Exponential Mean and Variance Example � In a large corporate computer network, user log-ons to the system can be modeled by a Poisson process with a mean of 25 log-ons per hour. � Let X denote the time in hours from the start of the interval until the first log-on. � What -in? is the mean and standard deviation of the time until the next log 6

Exponential Example 1 � � � In a large corporate computer network, user log-ons to the system can be modeled by a Poisson process with a mean of 25 log-ons per hour. Let X denote the time in hours from the start of the interval until the first log-on. What is the probability that there are no log-ons in the next 6 minutes (0. 1 hour)? By integrating the PDF Or use the CDF 7

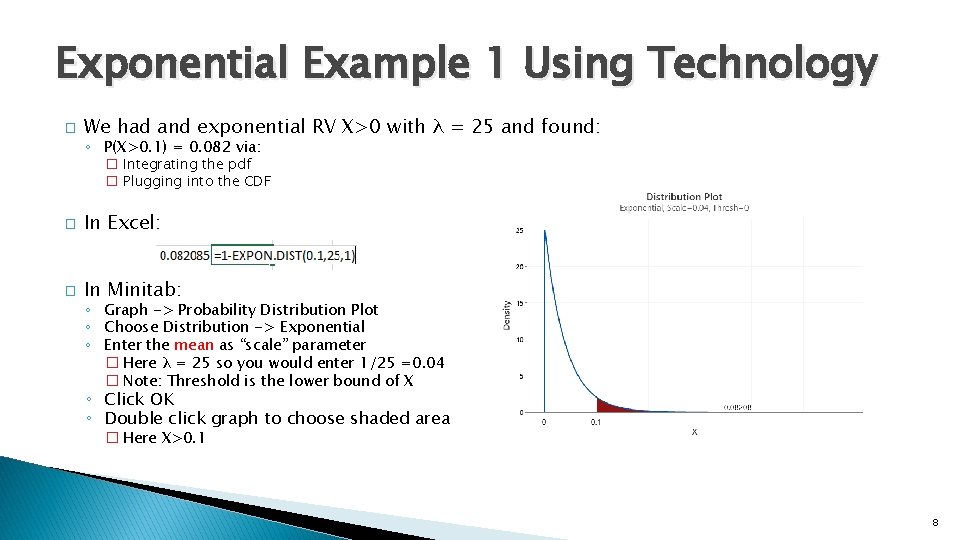
Exponential Example 1 Using Technology � We had and exponential RV X>0 with λ = 25 and found: ◦ P(X>0. 1) = 0. 082 via: � Integrating the pdf � Plugging into the CDF � In Excel: � In Minitab: ◦ Graph -> Probability Distribution Plot ◦ Choose Distribution -> Exponential ◦ Enter the mean as “scale” parameter � Here λ = 25 so you would enter 1/25 =0. 04 � Note: Threshold is the lower bound of X ◦ Click OK ◦ Double click graph to choose shaded area � Here X>0. 1 8

Exponential Example 2 � � � In a large corporate computer network, user log-ons to the system can be modeled by a Poisson process with a mean of 25 log-ons per hour. Let X denote the time in hours from the start of the interval until the first log-on. What is the probability that the time until the next log-on is between 2 and 3 minutes (0. 033 & 0. 05 hours)? By integrating the PDF Or use the CDF 9

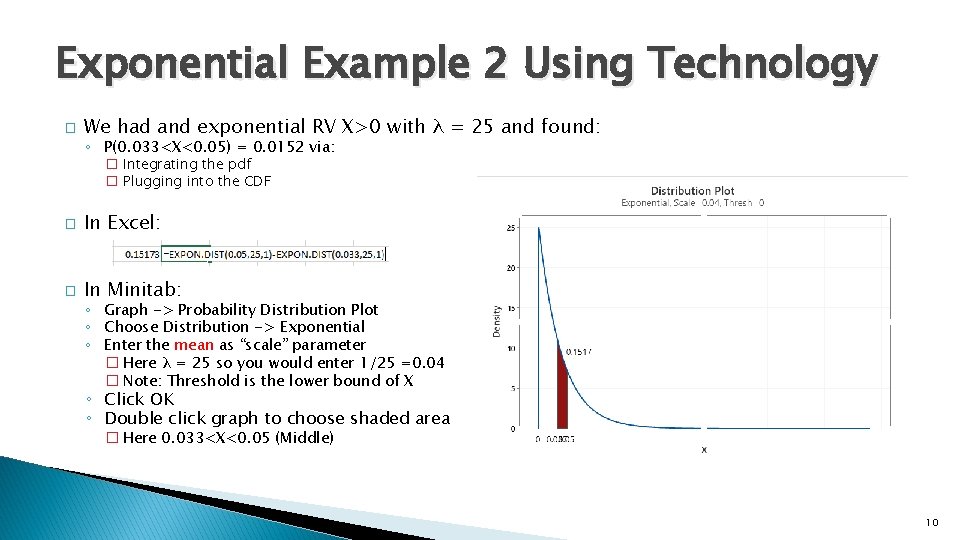
Exponential Example 2 Using Technology � We had and exponential RV X>0 with λ = 25 and found: ◦ P(0. 033<X<0. 05) = 0. 0152 via: � Integrating the pdf � Plugging into the CDF � In Excel: � In Minitab: ◦ Graph -> Probability Distribution Plot ◦ Choose Distribution -> Exponential ◦ Enter the mean as “scale” parameter � Here λ = 25 so you would enter 1/25 =0. 04 � Note: Threshold is the lower bound of X ◦ Click OK ◦ Double click graph to choose shaded area � Here 0. 033<X<0. 05 (Middle) 10

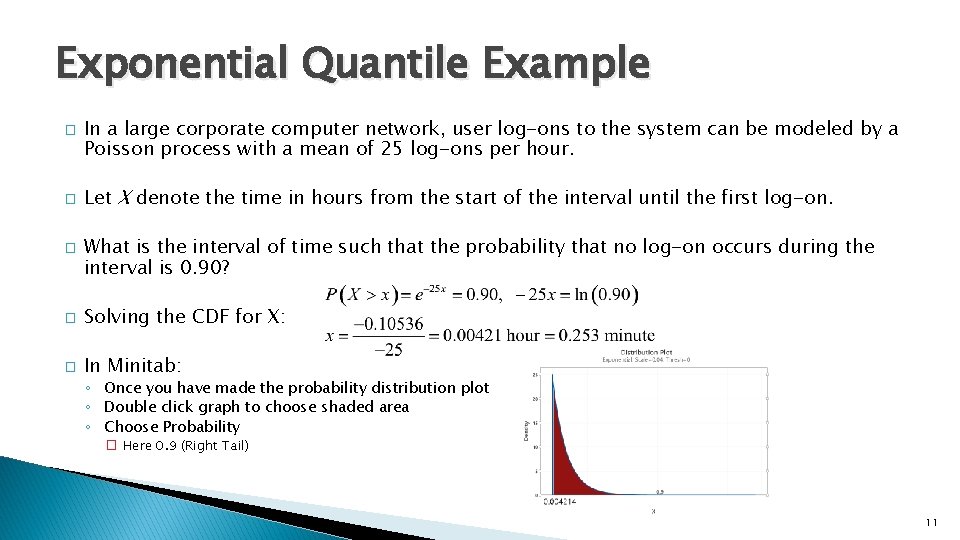
Exponential Quantile Example � � � In a large corporate computer network, user log-ons to the system can be modeled by a Poisson process with a mean of 25 log-ons per hour. Let X denote the time in hours from the start of the interval until the first log-on. What is the interval of time such that the probability that no log-on occurs during the interval is 0. 90? � Solving the CDF for X: � In Minitab: ◦ Once you have made the probability distribution plot ◦ Double click graph to choose shaded area ◦ Choose Probability � Here 0. 9 (Right Tail) 11