The Exponential Distribution 1 The Exponential Distribution Introduction

The Exponential Distribution 1

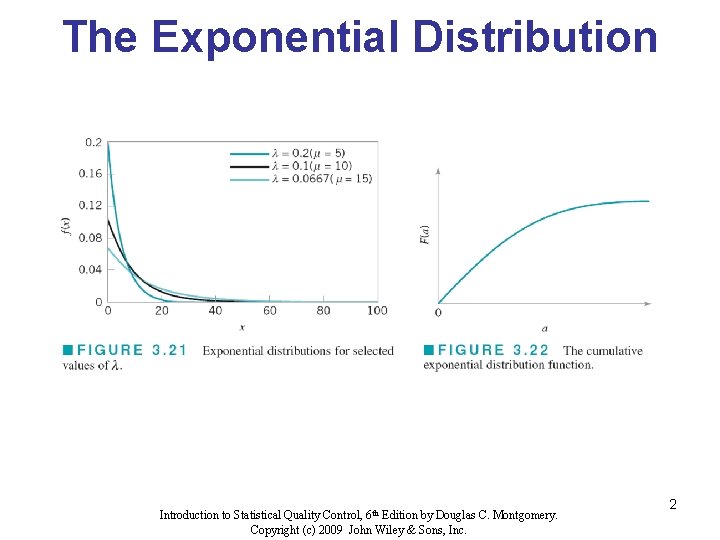
The Exponential Distribution Introduction to Statistical Quality Control, 6 th Edition by Douglas C.

The Weibull Distribution 3

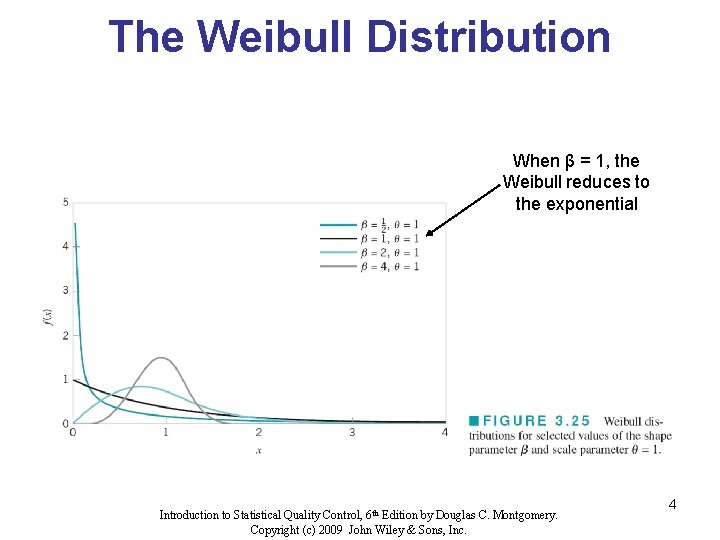
The Weibull Distribution When β = 1, the Weibull reduces to the exponential Introduction to Statistical Quality Control, 6 th Edition by Douglas C. Montgomery. Copyright (c) 2009 John Wiley & Sons, Inc. 4

Distributions Applicable to Reliability: 1. Exponential distribution. 2. Normal distribution. 3. Weibull distribution. 5

Distributions Applicable to Reliability Curves: The reliability curves for the exponential, normal and Weibull distributions as a function of time (Shown in the next slide). 6

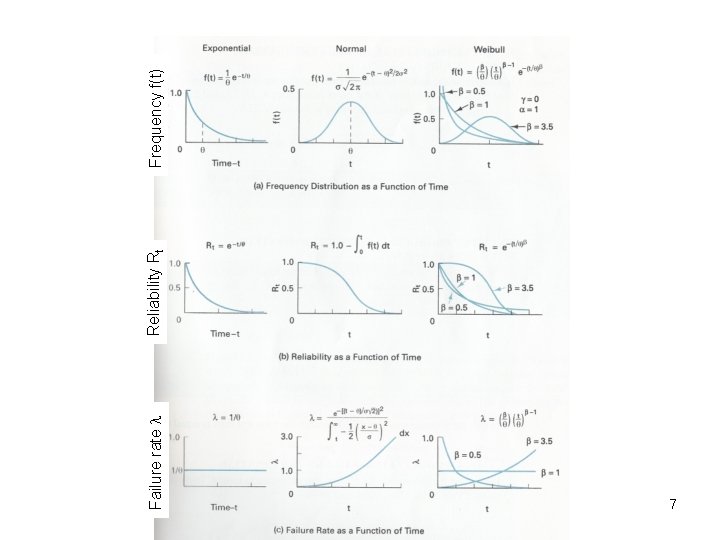
Failure rate 7 Reliability Rt Frequency f(t)

Distributions Applicable to Reliability Failure-Rate Curve: 1. It is important in describing the lifehistory curve of a product. 8

Distributions Applicable to Reliability 2. The curve, sometimes referred to as the “bathtub” curve, is a comparison of failure rate with time. 3. It has three distinct phases: 1. The debugging phase. 2. The chance failure phase. 3. The wear-out phase. 9

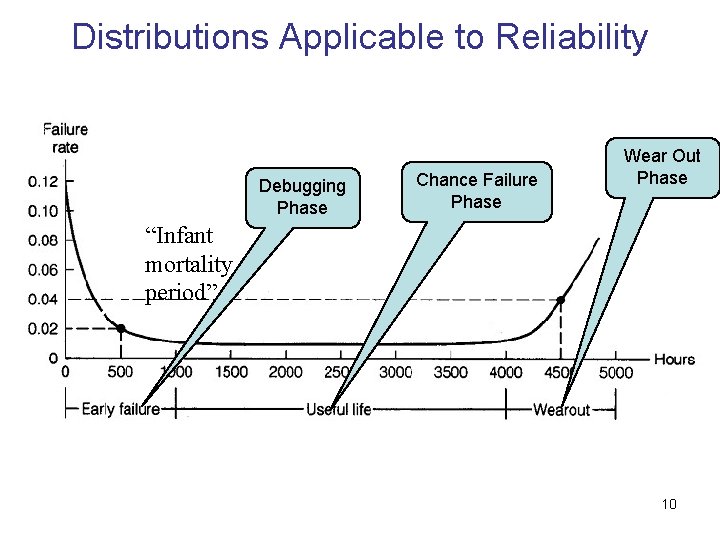
Distributions Applicable to Reliability Debugging Phase Chance Failure Phase Wear Out Phase “Infant mortality period” 10

Distributions Applicable to Reliability 1. The debugging phase: It is characterized by marginal and shortlife parts that cause a rapid decrease in the failure rate. It may be part of the testing activity prior to shipment for some products. The Weibull distribution ß<1 is used to describe the occurrence of failures. 11

Distributions Applicable to Reliability 2. The chance failure phase: Failures occur in a random manner due to the constant failure rate. The Exponential and the Weibull distributions β= 1 are best suited to describe this phase. 3. The wear-out phase: Is depicted by a sharp raise in failure rates. The Normal distribution and the Weibull distribution ß >1 are used to describe this 12 phase.

Normal Failure Analysis • The Normal distribution for reliability in the wear out phase. R(t): Reliability at time t P(t): Probability of failure or area of the normal curve to the left of time t. Table A. 13

Exponential Failure Analysis • Exponential distribution for reliability in the chance failure phase : Rt = e –t/ө Where: t: Time or cycles. ө: Mean life. 14

Weibull Failure Analysis • Exponential distribution for reliability for all phases • Can be used for the debugging phase (ß<1) and the chance failure phase (ß=1). • By setting = 1, the Weibull equals the exponential. • By setting ß=3. 4, the Weibull approximates the Normal. Rt = e –(t/ө)ß Where ß is the Weibull slope. 15