The Evolution of Proofs in Computer Science Yael

The Evolution of Proofs in Computer Science Yael Tauman Kalai Microsoft Research

What is a Proof? Mathematical proofs: • Developed by ancient Greek mathematicians [Thales, Eudoxus, Theaetetus, Atistotle 600 BCE] • [Euclid 300 BCE] Introduced axiomatic method, theorems are proved using deductive logic. • Proof theory: well studied branch of mathematics [Hilbert 19 th century]

Classical Proofs

Zero-Knowledge Proofs [Goldwasser-Micali-Rackoff 85]

Zero-Knowledge Proofs [Goldwasser-Micali-Rackoff 85]

Interactive Proofs [Goldwasser-Micali-Rackoff 85] [Goldreich-Micali-Wigderson 87]:

Interactive Proofs are More Efficient! [Lund-Fortnow-Karloff-Nissan 90, Shamir 90] Example: Chess

Interactive Proofs are More Efficient! [Lund-Fortnow-Karloff-Nissan 90, Shamir 90] correctness of any computation can be proved: Time to verify Space required to do the computation

Multi-Prover Interactive Proofs [Ben. Or-Goldwasser-Kilian-Wigderson 88]

The Power of Multi-Prover Interactive Proofs (MIPs) [Babai-Fortnow-Lund 90] Any proof can be made exponentially shorter with a 2 -prover interactive proof!

[Fortnow-Rompel-Sipser 88]:

[Fortnow-Rompel-Sipser 88]:

Probabilistically Checkable Proofs V [Feige-Goldwasser-Lovasz-Safra-Szegedy 91, Babai-Fortnow-Levin. Szegedy 91, Arora-Safra 92, Arora-Lund-Mutwani-Sudan-Szegedy 92] PCP Theorem: Every proof can be converted to a probabilistically checkable one (of almost same size) that can be verified by reading only constant number of its bits.

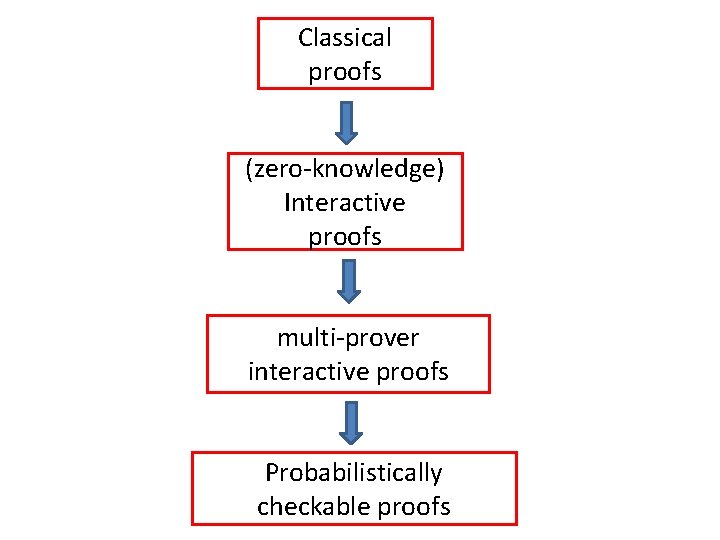
Classical proofs (zero-knowledge) Interactive proofs multi-prover interactive proofs Probabilistically checkable proofs

Fast Forward to Today’s Reality

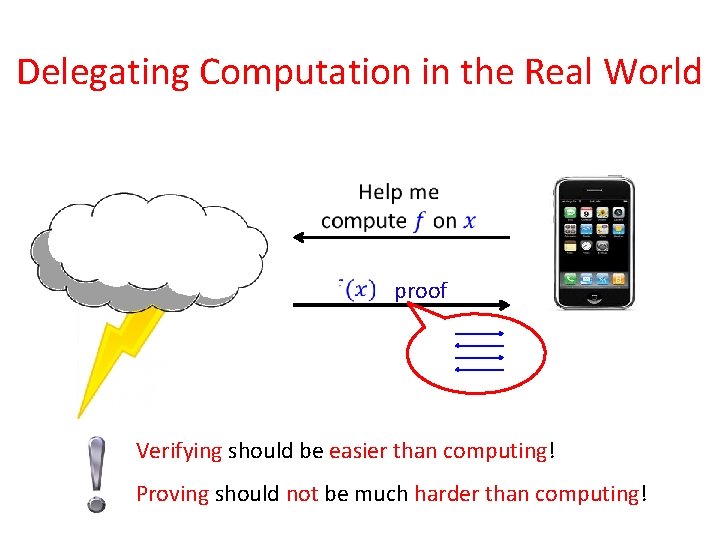
Delegating Computation in the Real World proof Verifying should be easier than computing! Proving should not be much harder than computing!

Interactive Proofs not useful for real world delegation Verifying is easier that computing (time to verify proportional to space of computation) Proving is harder than computing

Interactive Proofs useful for real world delegation [Goldwasser-Kalai-Rothblum 08] Proving is not harder than computing Only for functions computable by low depth circuits

Computationally-Sound Proofs [Micali 94] A delegation scheme for all functions. Computational soundness: Cheating is possible, but requires too much work, assuming hardness assumption hash proof certificate! [Kilian 92] no satisfying proofunder of security Secure standard assumption

2 -Message Delegation Scheme [Aiello-Bhatt-Ostrovsky-Rajagopalan 2000, Dwork. Langberg-Naor-Nissim-Reingold 2004, Kalai-Raz 2009, Groth 10, Gennaro-Gentry-Parno 2010 , Chung-Kalai. Vadhan 2010, Applebaum-Ishai-Kushilevitz 2010, Gentry. Wichs 2011, Parno-Raykova-Vaikuntanathan 2011, Benabbas-Gennaro-Vahlis 2011, Goldwasser-Lin. Rubinstein 2011, Damgard-Faust-Hazay 2011, Lipma 12, Fiore-Gennaro 2012, Bitansky-Canetti-Chiesa. Tromer 2012 a, Bitansky-Canetti-Chiesa-Tromer 2012 b, Gennaro-Gentry-Parno-Raykova 2012, Kalai-Raz. Rothblum 2013, Kalai-Raz-Rothblum 2014]

[Kalai-Raz-Rothblum 2014]: 2 -message delegation scheme for all functions under standard hardness assumptions No-signalling strategies [Khaln-Tsirelson 85, Rastall 85] special relativity theory: information does not travel faster than the speed of light

No-Signalling Strategies

Multi-Prover Interactive Proofs (MIPs) • Classical soundness: [Babai-Fortnow-Lund 90]: MIP for all functions • Quantum soundness: [Ito-Vidick 2012]: MIP for all functions • No-Signalling soundness: [Kalai-Raz-Rothblum 2014]: MIP for all functions

[Kalai-Raz-Rothblum 2014]: No-signalling multi-prover interactive proofs for all functions 2 -message delegation for all functions under standard hardness assumptions

[Kalai-Raz-Rothblum 2014]: MIP sound against no-signalling provers 2 -msg delegation [Aiello-Bhatt-Ostrovsky-Sivarama 00] secure for every FHE with sub-exponential security

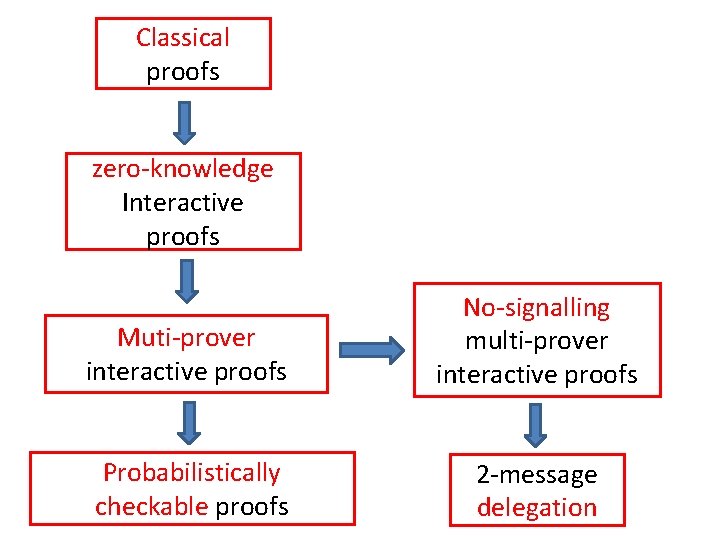
Classical proofs zero-knowledge Interactive proofs Muti-prover interactive proofs No-signalling multi-prover interactive proofs Probabilistically checkable proofs 2 -message delegation

Delegation in Practice [Cormode-Mitzenmacher-Thaler 2012] [Thaler-Roberts-Mitzenmacher-Pfister 2012] [Thaler 2013] [Vu-Setty-Blumberg-Walfish 2013] [Ben. Sasson-Chiesa-Genkin-Tromer-Virza 2013] [Parno-Gentry-Howell-Raykova 2013]

Thank You!