THE EVALUATION APPLICATION OF HYDRUS2 D MODEL FOR

THE EVALUATION / APPLICATION OF HYDRUS-2 D MODEL FOR SIMULATING MACRO-PORES FLOW IN LOESS SOIL XU Xuexuan , HUA Rui, GAO Zhaoxia 24 Aug. 2016 1

CONTENTS 1. Research Background 2. Materials and Methods 3. Hydrus 2 D Simulating 4. Discussion and Conclusions 2

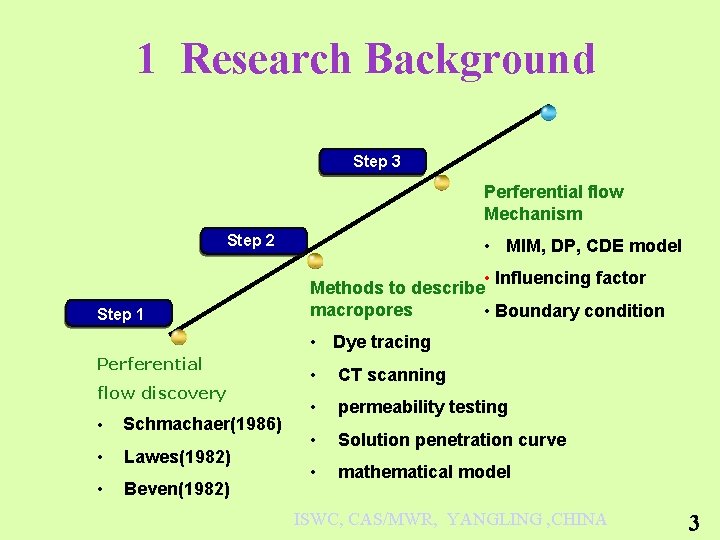
1 Research Background Step 3 Perferential flow Mechanism Step 2 Step 1 • MIM, DP, CDE model • Influencing factor Methods to describe macropores • Boundary condition • Dye tracing Perferential flow discovery • Schmachaer(1986) • Lawes(1982) • Beven(1982) • CT scanning • permeability testing • Solution penetration curve • mathematical model ISWC, CAS/MWR, YANGLING , CHINA 3

Tableland gully Region in the South part of loess plateau 4

2 Materials and Methods Soil properties The experimental soil was Heilu soil. The initial bulk density was 1. 3 g∙cm-3。 Table 1 soil particle size distribution Particle size % 2~0. 25 mm 0. 25~0. 05 mm 0. 05~0. 01 mm 0. 001~0. 01 mm 0~0. 001 mm 0. 10 7. 17 57. 78 20. 89 14. 18 According the particle size distribution, it is the clay soil 5

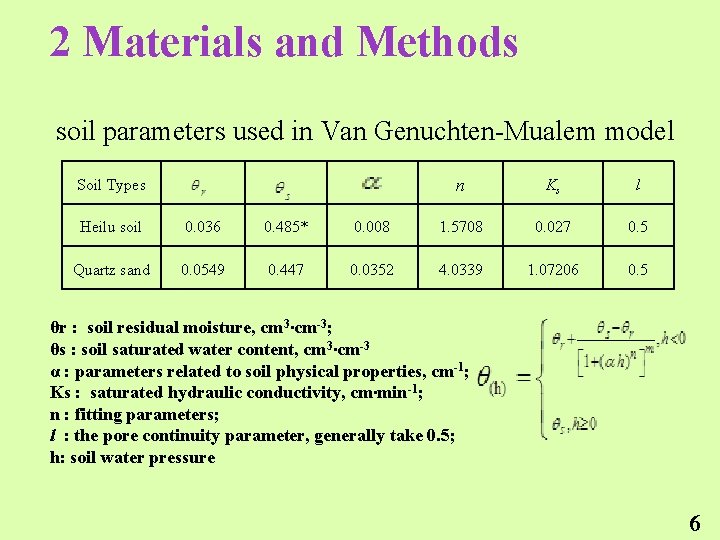
2 Materials and Methods soil parameters used in Van Genuchten-Mualem model Soil Types n Ks l Heilu soil 0. 036 0. 485* 0. 008 1. 5708 0. 027 0. 5 Quartz sand 0. 0549 0. 447 0. 0352 4. 0339 1. 07206 0. 5 θr : soil residual moisture, cm 3∙cm-3; θs : soil saturated water content, cm 3∙cm-3 α : parameters related to soil physical properties, cm-1; Ks : saturated hydraulic conductivity, cm∙min-1; n : fitting parameters; l : the pore continuity parameter, generally take 0. 5; h: soil water pressure 6

2 Materials and Methods l experimental device stainless steel wire mesh (60 mesh) fɸ= 0. 5 cm steel wire strips 7

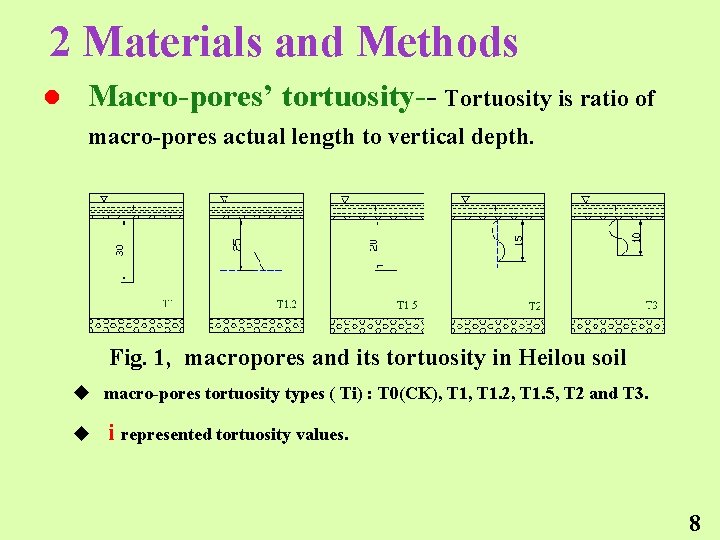
2 Materials and Methods l Macro-pores’ tortuosity-- Tortuosity is ratio of macro-pores actual length to vertical depth. Fig. 1, macropores and its tortuosity in Heilou soil u macro-pores tortuosity types ( Ti) : T 0(CK), T 1. 2, T 1. 5, T 2 and T 3. u i represented tortuosity values. 8

2 Materials and Methods l The macro-pores’ Continuity Figure 2: Six types of macro-pores Continuity O—Open, means connected with soil surface or the bottom of the outflow port; C---Closed, means disconnected with the soil surface or not connected with the bottom of the outflow port; N(n) was the length and number of macro-pores. L or S was macro-pores shape. 9

2 Materials and Method—HYDRUS-2 D u 10

3 Hydrus 2 D Simulating Definite conditions of soil macro-pores flow movement soil box contained three layers : quartz sand(EH) = 1 cm, soil (HI)=60 cm, and quartz sand(ID)= 3 cm AE=6 cm, AB=30 cm. h 0 is the initial suction. It could be considered that water instantly filled pores after experiment started in open macro-pores soil column. the pressure head linearly increased with macro-pores depth increased 11

3 Hydrus 2 D Simulating p Close macro-pores boundary: When the water did not reach, the water flux was zero. When the water reached and the soil was saturated, the water pressure was zero. p Neither of upper nor lower connected macro-pores : due to the larger longitudinal computational domain, it could be considered soil water couldn’t reach the bottom boundary in the calculation time, and no water exchanged in boundary. p Both up and down connected macro-pores in the soil column, the water would quickly flow through the soil and produce runoff. Where: t 0 is the critical value of the flux change time, min; q 1, q 2 represent flux values: determined by the measured values. 12

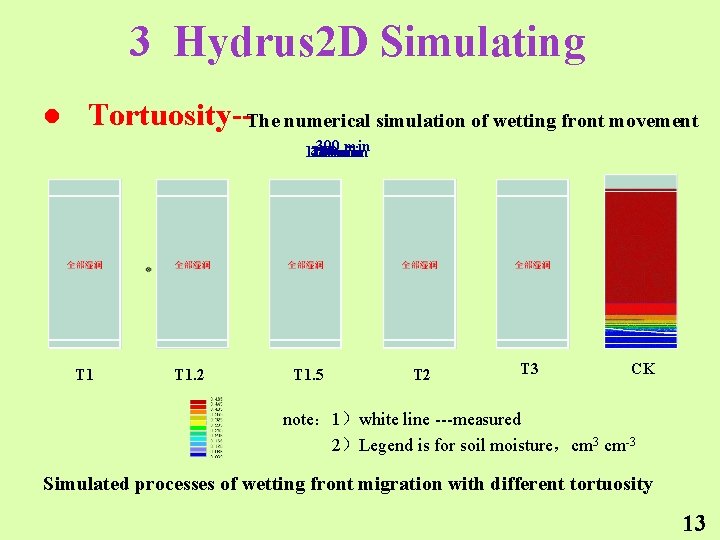
3 Hydrus 2 D Simulating l Tortuosity--The numerical simulation of wetting front movement 300 min 120 240 420 180 60 10 min min T 1 T 1. 2 T 1. 5 T 2 T 3 CK note： 1）white line ---measured 2）Legend is for soil moisture，cm 3 cm-3 Simulated processes of wetting front migration with different tortuosity 13

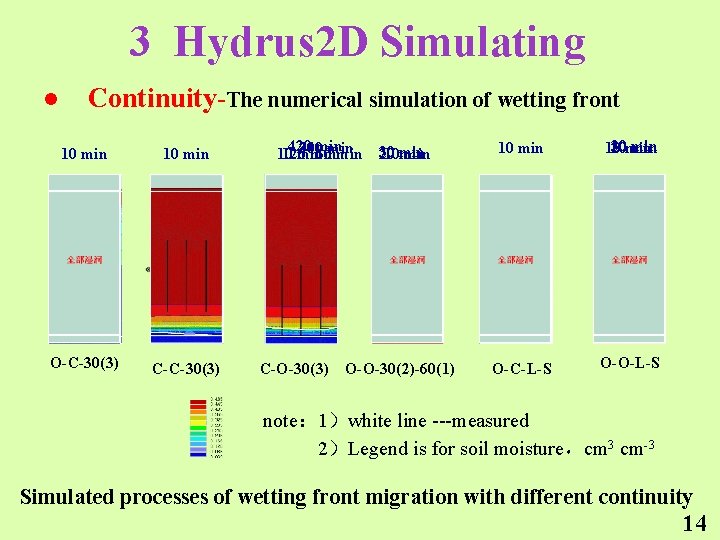
3 Hydrus 2 D Simulating l Continuity-The numerical simulation of wetting front 10 min 420 min 240 300 10 120 min 60 min 30 20 10 min 10 min 30 min 10 20 min O-C-30(3) C-O-30(3) O-O-30(2)-60(1) O-C-L-S O-O-L-S note： 1）white line ---measured 2）Legend is for soil moisture，cm 3 cm-3 Simulated processes of wetting front migration with different continuity 14

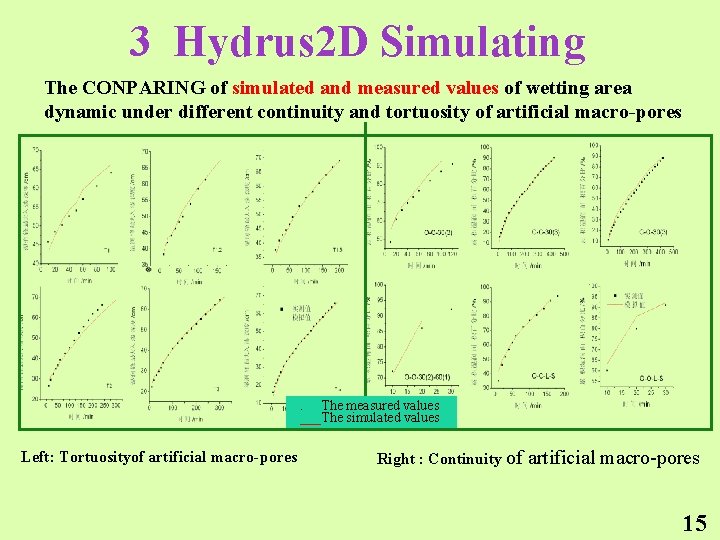
3 Hydrus 2 D Simulating The CONPARING of simulated and measured values of wetting area dynamic under different continuity and tortuosity of artificial macro-pores . The measured values ___The simulated values Left: Tortuosityof artificial macro-pores Right : Continuity of artificial macro-pores 15

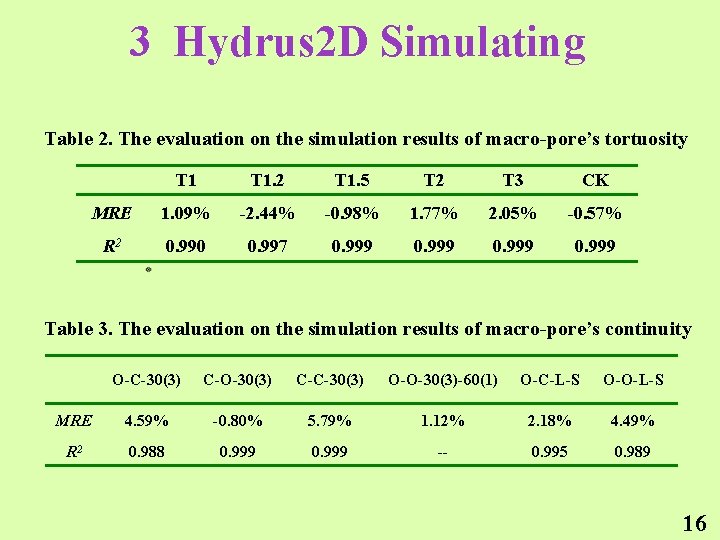
3 Hydrus 2 D Simulating Table 2. The evaluation on the simulation results of macro-pore’s tortuosity T 1. 2 T 1. 5 T 2 T 3 CK MRE 1. 09% -2. 44% -0. 98% 1. 77% 2. 05% -0. 57% R 2 0. 990 0. 997 0. 999 Table 3. The evaluation on the simulation results of macro-pore’s continuity O-C-30(3) C-O-30(3) C-C-30(3) O-O-30(3)-60(1) O-C-L-S O-O-L-S MRE 4. 59% -0. 80% 5. 79% 1. 12% 2. 18% 4. 49% R 2 0. 988 0. 999 -- 0. 995 0. 989 16

4 Discussion and Conclusions p. Convection–dispersion equation (CDE model) in porous media is not fitted for structured soil. p. Two-domain flow models is much good at simulating water flow when preferential flow occurs. DP (dualpermeability) model is better than MIM model (mobile and immobile regions moddel) p. Hydrus model (MIM and DP models) was based on theory of soil water movement in heterogeneous medium. Therefore, the Hydrus model was much more perfect theoretically than CDE models. 17

4 Discussion and Conclusions p. Hydrus-2 D can be used to simulate soil wetting front process containing different tortuosity and continuity macro-pores in loess soil. MRE less than 5%, R 2 greater than 0. 9. p It was illustrated that the established Hydrus-2 D model and the definite conditions of model were feasible and reasonable. Namely, Hydrus-2 D model could simulate the infiltration behavior in loess soil, and the basic hydraulic parameters of Heilu soil are also reasonable. p. Our research therefore agree with many previous researches, and also support that structure soil obviously contained more macopores, and its water flow could be chartered largely by the hydrus 2 D model. 18

Prof. XUXue-xuan Institute of soil and water conservation, CAS & MWR No. 26, Xinong Road, Yangling, Shaanxi, CHINA Postcode: 712100 Thank you Contact Us Phone: 13709229201 Email: xuxuexuan@nwsuaf. edu. cn 19