The Equipartition Theorem in Classical Statistical Mechanics ONLY

The Equipartition Theorem in Classical Statistical Mechanics (ONLY!)

The Equipartition Theorem in Classical Statistical Mechanics (ONLY!) It states: “Each degree of freedom in a system of particles contributes (½)k. BT to thermal average energy Ē of the system. ”

The Equipartition Theorem is Valid in Classical Stat. Mech. ONLY!!! “Each degree of freedom in a system of particles contributes (½)k. BT to thermal average energy Ē of the system. ” Note: 1. This is strictly valid only if each term in the classical energy is proportional to a momentum (p) squared or to a coordinate (q) squared. 2. The degrees of freedom are associated with translation, rotation & vibration of the system’s molecules.

• In the Classical Cannonical Ensemble, it is straightforward to prove that The average energy Ē of a particle per independent degree of freedom = (½)k. BT. Outline of a Proof Follows:

Proof: System Total Energy Sum of single particle energies: System Partition Function Z Note: This is Classical Stat Mech. , so these sums should be really be phase space integrals! Z' , Z'' , etc. = Partition function for each particle.

System Partition Function Z Z = Product of partition functions Z' , Z'' , etc. of each particle Canonical Ensemble “Recipe” for the Mean (Thermal) Energy Ē U So, the Thermal Energy per Particle is:

• Contributions to the Classical Energy of each particle: = KEt + KEr + KEv + PEv + …. • Translational Kinetic Energy: KEt = (½)mv 2 = [(p 2)/(2 m)] • Rotational Kinetic Energy: KEr = (½)I 2 • Vibrational Potential Energy: PE = (½)kx 2

Proof Continued! • Assume that each degree of freedom has energy that is proportional to a p 2 or to a q 2. With this assumption, the total energy has the form: • Plus a similar sum containing (qi)2 • For simplicity, focus on the p 2 sum above:

Proof Continued! • For each particle, change the sum into an integral over momentum, as below. • It is a Gaussian & is tabulated. Ki ½ (½)(π/bi)

Proof Continued! Ki (½)(π/bi)½ • The system partition function Z is then proportional to the product of integrals like above. • Or, Z is proportional to the quantity P: • Finally, Z can be written:

• Use the Canonical Ensemble “Recipe” to get the average energy per particle per independent degree of freedom f:

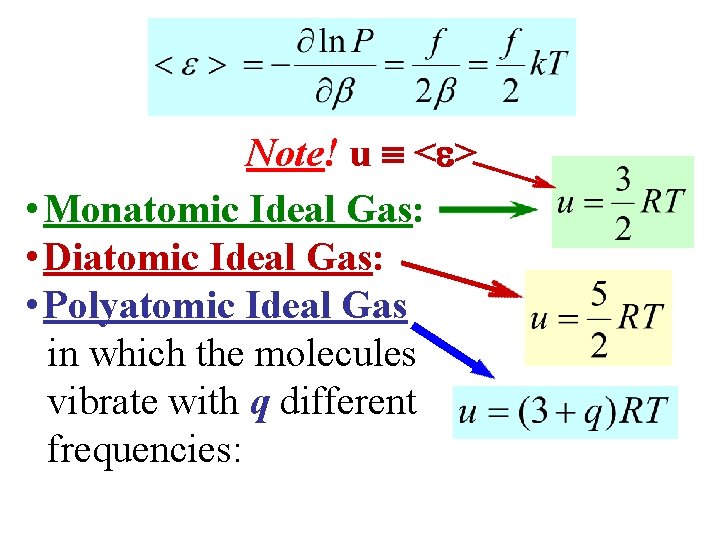
Note! u < > • Monatomic Ideal Gas: • Diatomic Ideal Gas: • Polyatomic Ideal Gas in which the molecules vibrate with q different frequencies: