The end of affine cameras Affine SFM revisited

The end of affine cameras • Affine SFM revisited • Epipolar geometry • Two-view structure from motion • Multi-view structure from motion Planches : – http: //www. di. ens. fr/~ponce/geomvis/lect 3. pptx – http: //www. di. ens. fr/~ponce/geomvis/lect 3. pdf

Weak-Perspective Projection Model (p and P are in homogeneous coordinates) r p=MP (P is in homogeneous coordinates) p=AP+b (neither p nor P is in hom. coordinates)

Affine Spaces: (Semi-Formal) Definition

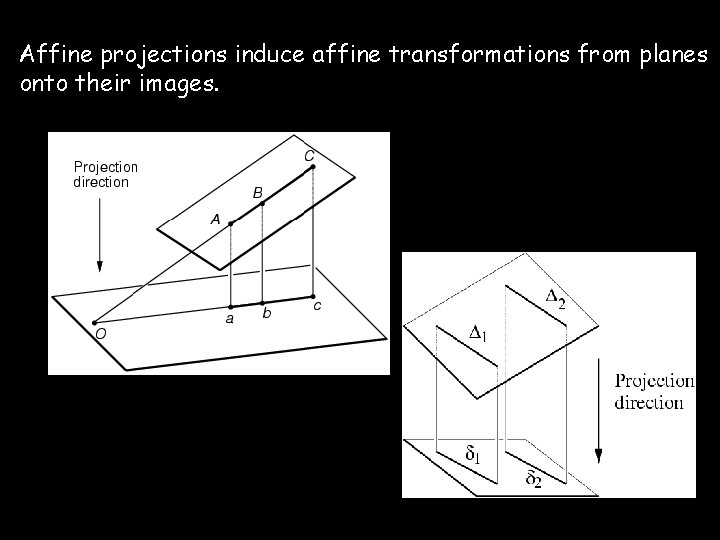
Affine projections induce affine transformations from planes onto their images.

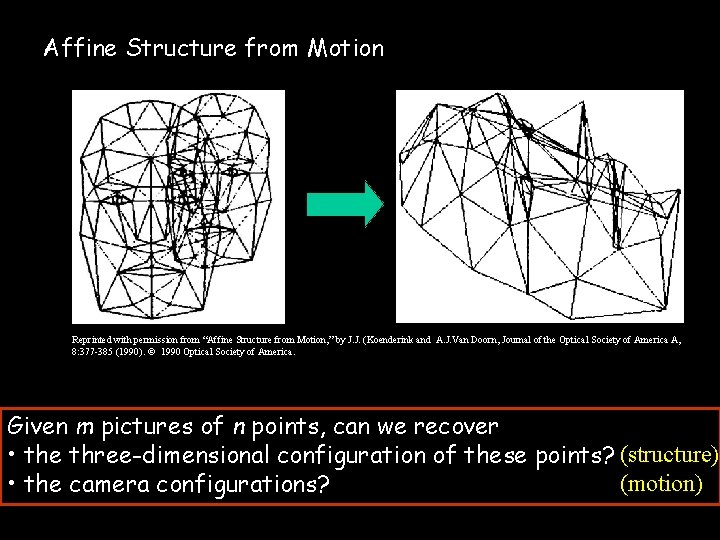
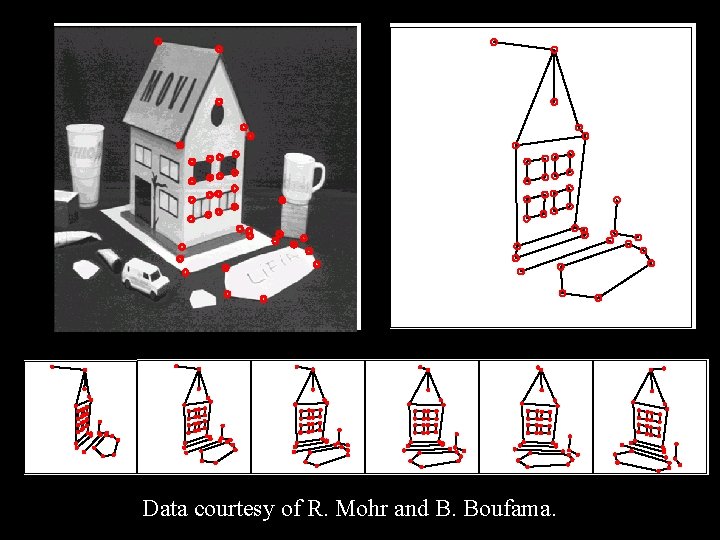
Affine Structure from Motion Reprinted with permission from “Affine Structure from Motion, ” by J. J. (Koenderink and A. J. Van Doorn, Journal of the Optical Society of America A, 8: 377 -385 (1990). 1990 Optical Society of America. Given m pictures of n points, can we recover • the three-dimensional configuration of these points? (structure) (motion) • the camera configurations?

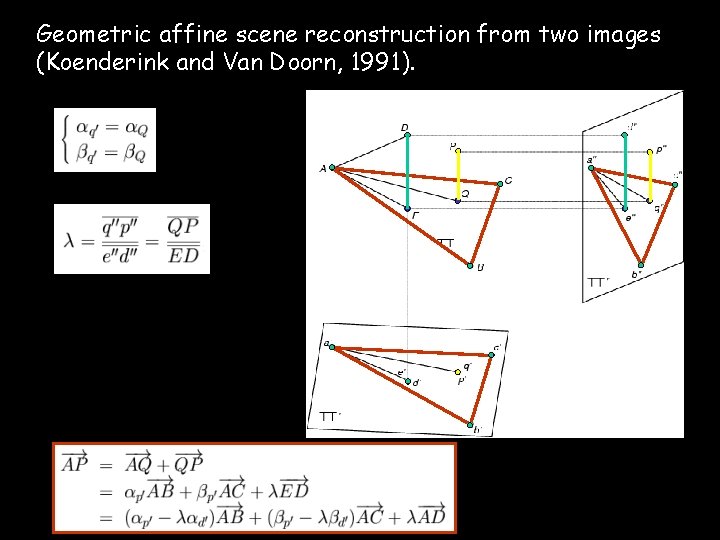
Geometric affine scene reconstruction from two images (Koenderink and Van Doorn, 1991).

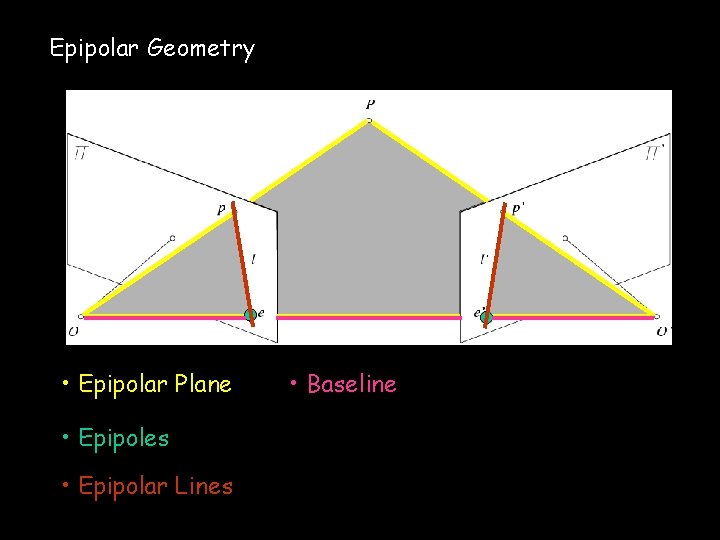
Epipolar Geometry • Epipolar Plane • Epipoles • Epipolar Lines • Baseline

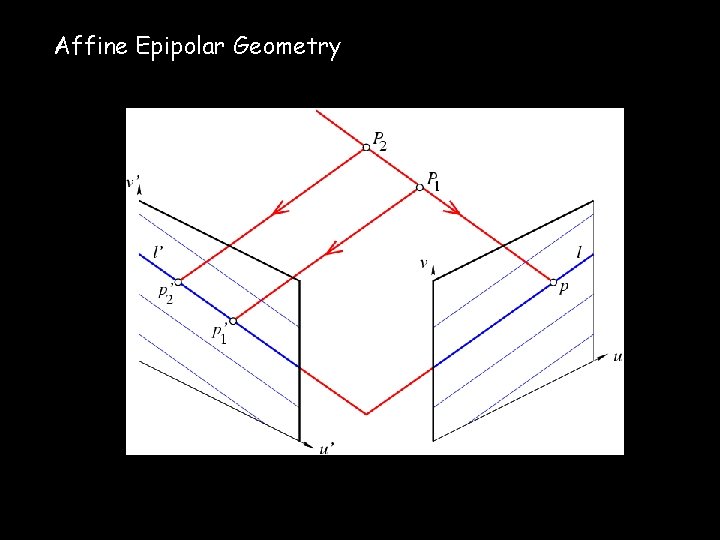
The Affine Epipolar Constraint Note: the epipolar lines are parallel.

Affine Epipolar Geometry

The Affine Fundamental Matrix where

Data courtesy of R. Mohr and B. Boufama.

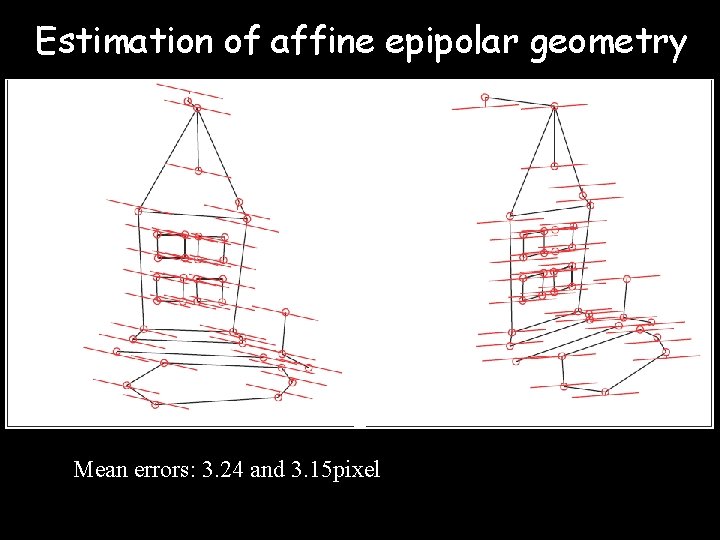
Estimation of affine epipolar geometry Mean errors: 3. 24 and 3. 15 pixel

The Affine Structure-from-Motion Problem Given m images of n fixed points P we can write j Problem: estimate the m 2 x 4 matrices M i and the n positions Pj from the mn correspondences p. ij 2 mn equations in 8 m+3 n unknowns Overconstrained problem, that can be solved using (non-linear) least squares!

The Affine Ambiguity of Affine SFM When the intrinsic and extrinsic parameters are unknown If M i and P are solutions, j So are M’i and P’ where j and Q is an affine transformation.

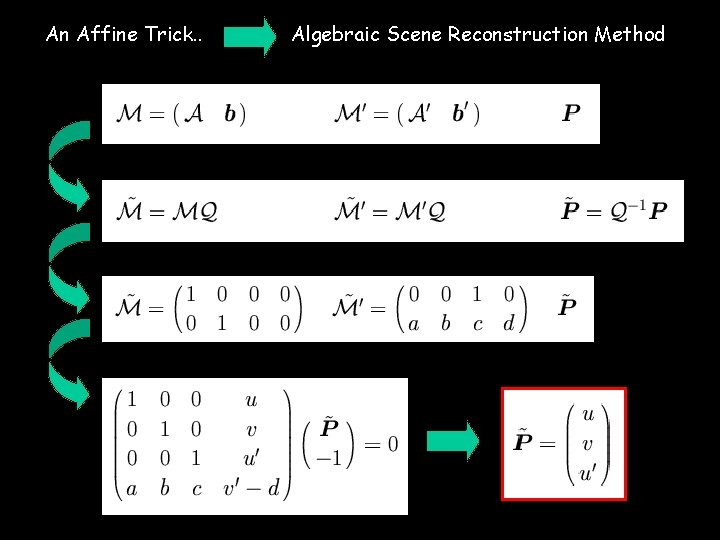
An Affine Trick. .

The Affine Epipolar Constraint Note: the epipolar lines are parallel.

An Affine Trick. . Algebraic Scene Reconstruction Method

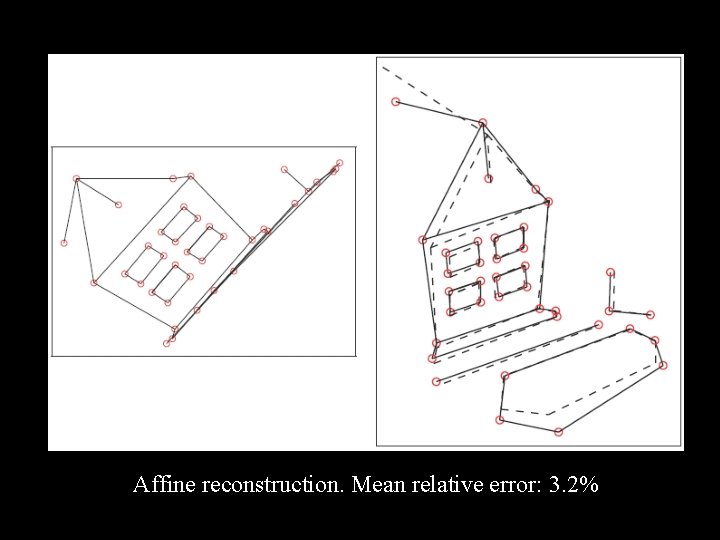
Affine reconstruction. Mean relative error: 3. 2%

The Affine Structure of Affine Images Suppose we observe a static scene with m fixed cameras. . The set m-tuples of all image points in a scene is a 3 D affine space!

has rank 4!

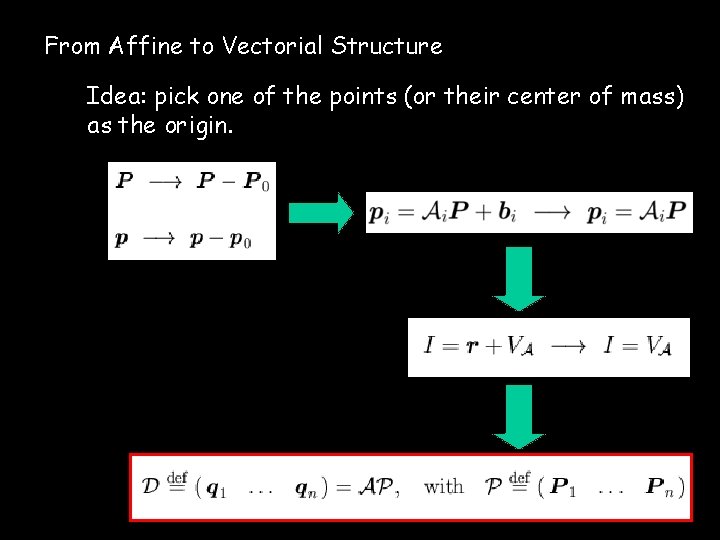
From Affine to Vectorial Structure Idea: pick one of the points (or their center of mass) as the origin.

What if we could factorize D? (Tomasi and Kanade, 1992) Affine SFM is solved!

Singular Value Decomposition

Singular Value Decomposition square roots of

Singular Value Decomposition

Singular Value Decomposition

What if we could factorize D? (Tomasi and Kanade, 1992) Affine SFM is solved! Singular Value Decomposition We can take

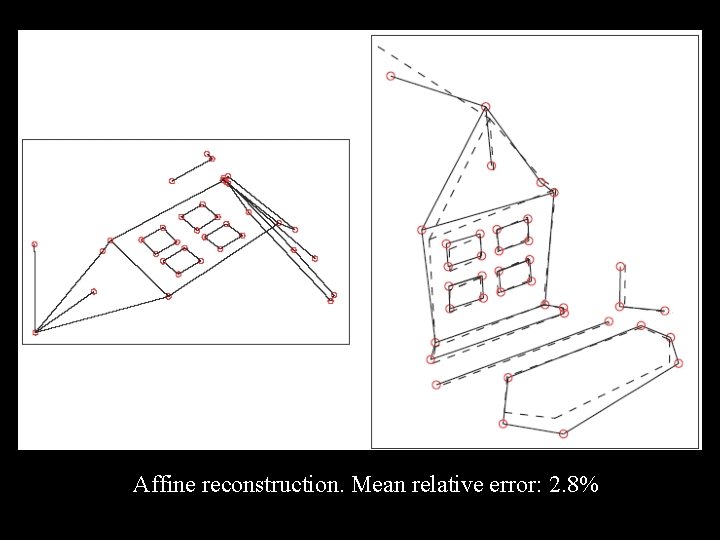
Affine reconstruction. Mean relative error: 2. 8%

Projective cameras • Motivation • Elements of Projective Geometry • Projective structure from motion

The Projective Structure-from-Motion Problem Given m perspective images of n fixed points P we can write j Problem: estimate the m 3 x 4 matrices i M and the n positions Pj from the mn correspondences p. ij 2 mn equations in 11 m+3 n unknowns Overconstrained problem, that can be solved using (non-linear) least squares!

The Projective Ambiguity of Projective SFM When the intrinsic and extrinsic parameters are unknown If M i and P are solutions, j So are M ’ and P ’ where i j and Q is an arbitrary non-singular 4 x 4 matrix. Q is a projective transformation.

Projective Spaces: (Semi-Formal) Definition

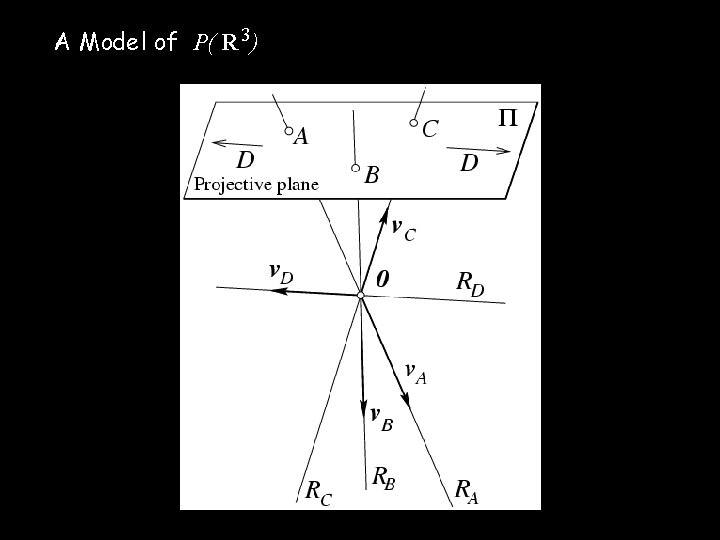
A Model of P( R 3)

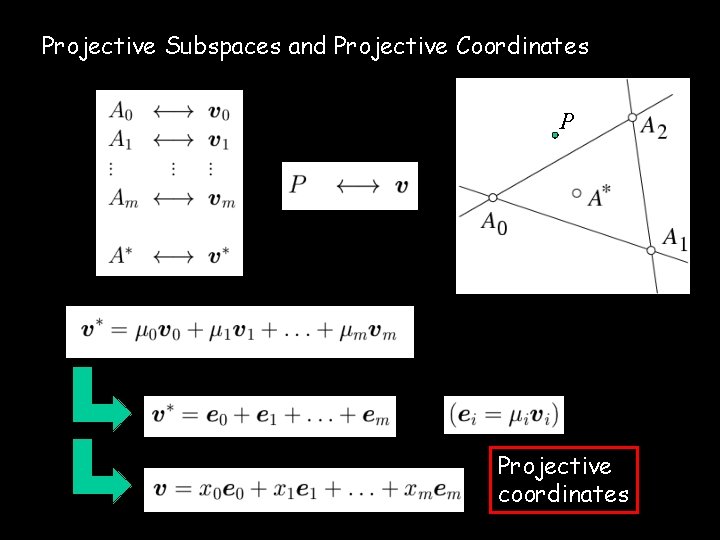
Projective Subspaces and Projective Coordinates

Projective Subspaces and Projective Coordinates P Projective coordinates

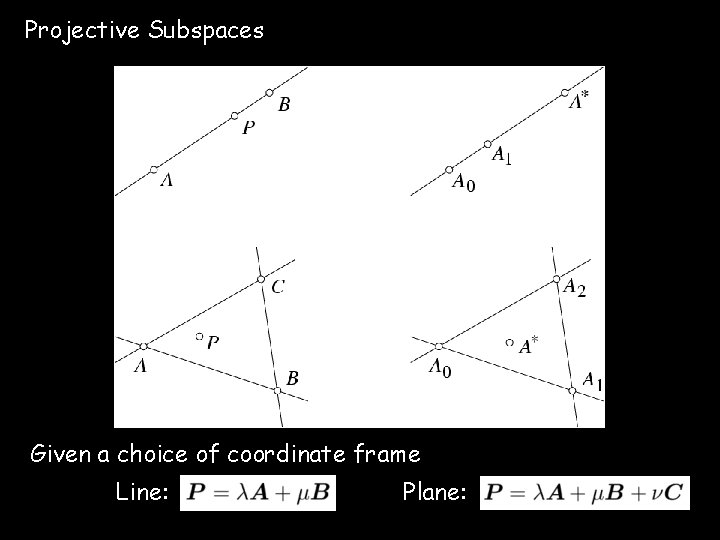
Projective Subspaces Given a choice of coordinate frame Line: Plane:

Hyperplanes and duality Consider n+1 points P 0, … , Pn-1, P in a projective space X of dimension n. They lie in the same hyperplane when Det(D)=0. This can be rewritten as u 0 x 0+u 1 x 1+…+unxn = 0, or T P = 0, where = (u 0, u 1, …, un)T. Hyperplanes form a dual projective space X* of X, and any theorem that holds for points in X holds for hyperplanes in X*. What is the dual of a straight line?

Affine and Projective Spaces

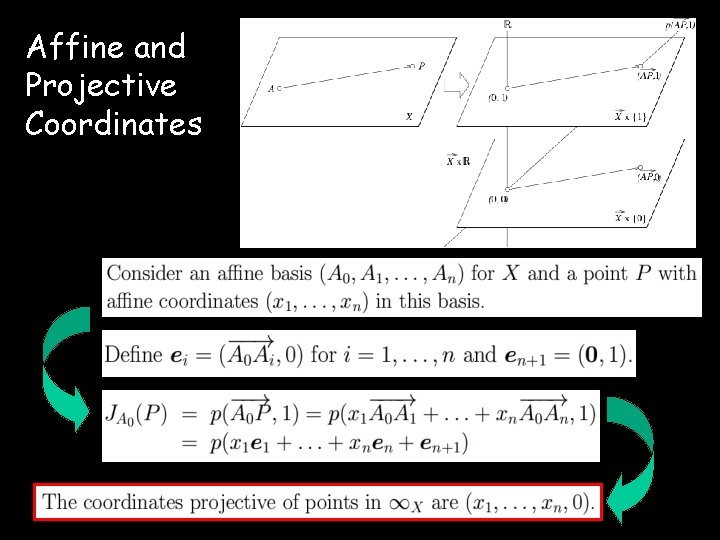
Affine and Projective Coordinates

Affine and Projective Coordinates