The Encoding Complexity of Network Coding Michael Langberg

The Encoding Complexity of Network Coding Michael Langberg California Institute of Technology Joint work with Jehoshua Bruck and Alex Sprintson 1

Multicast Networks • • Directed graph G=(V, E). s Source node s. Terminal nodes T={t 1, t 2, …}. t 3 Requirement: transfer information from s to T. t 2 t 1 G=(V, E) 2

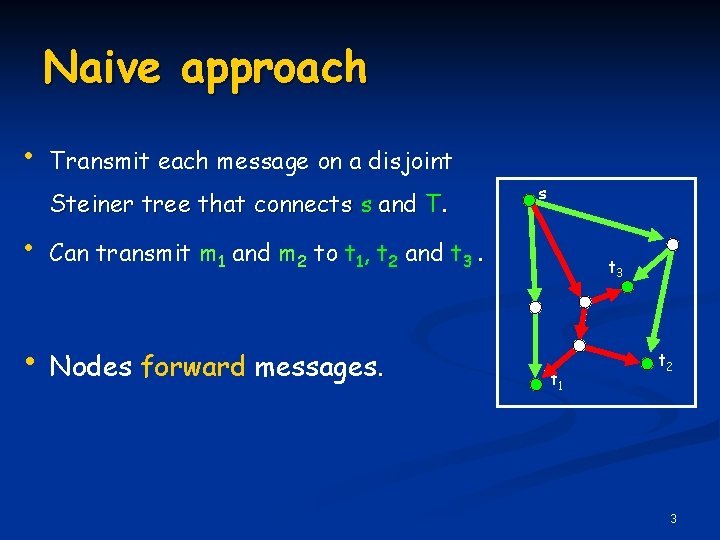
Naive approach • Transmit each message on a disjoint Steiner tree that connects s and T. • s Can transmit m 1 and m 2 to t 1, t 2 and t 3. • Nodes forward messages. t 3 t 1 t 2 3

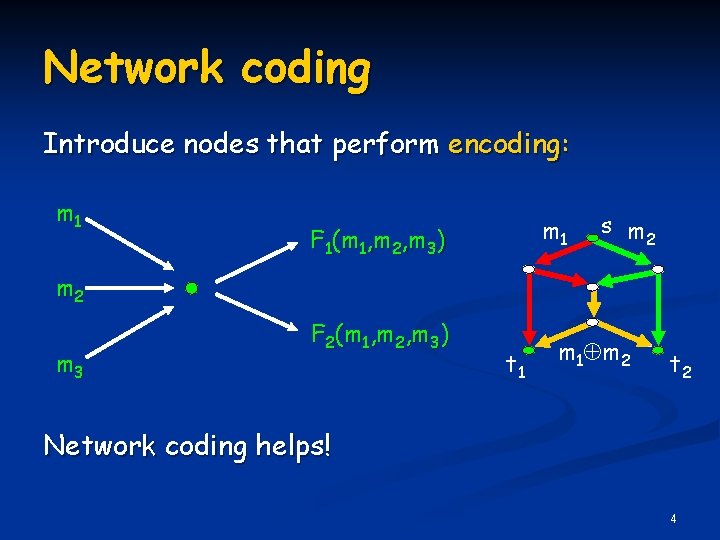
Network coding Introduce nodes that perform encoding: m 1 F 1(m 1, m 2, m 3) s m 2 m 3 F 2(m 1, m 2, m 3) t 1 m 2 t 2 Network coding helps! 4

m 1 “History” • t 1 s m 2 m 1 m 2 Network coding [Ahlswede. Cai. Li. Yeung 00, Li. Yeung. Cai 03]: t 2 Multicast Min-Cut condition: Multicast of h messages from s to T iff Min-Cut between s and each ti is at least h. h will be called the multicast capacity of G. • Can transmit at capacity using random linear combinations on each edge [Ho. Koetter. Medard. Karger. Effros 03]. 5

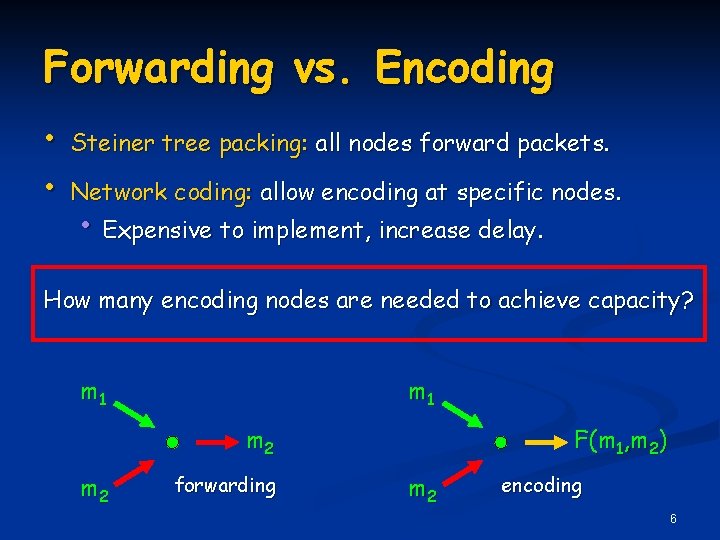
Forwarding vs. Encoding • • Steiner tree packing: all nodes forward packets. Network coding: allow encoding at specific nodes. • Expensive to implement, increase delay. How many encoding nodes are needed to achieve capacity? m 1 m 2 forwarding F(m 1, m 2) m 2 encoding 6

Our Goal • • • m 1 m 2 F(m 1, m 2) Input: Multicast network problem: • Single source, k terminals. • Capacity = h (Min-Cut condition). Goal: find a “coding scheme” that achieves capacity with minimum number of encoding nodes. Coding scheme: assigns a function F to each edge tying incoming information to outgoing information. 7

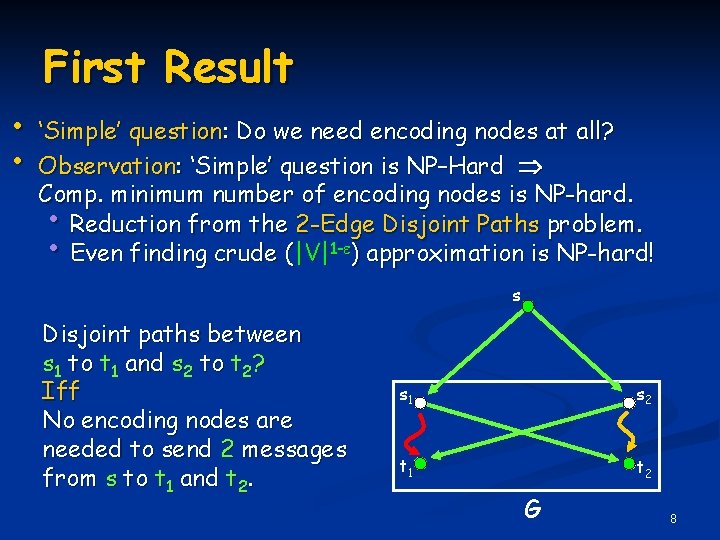
First Result • • ‘Simple’ question: Do we need encoding nodes at all? Observation: ‘Simple’ question is NP–Hard Comp. minimum number of encoding nodes is NP-hard. • Reduction from the 2 -Edge Disjoint Paths problem. • Even finding crude (|V|1 - ) approximation is NP-hard! s Disjoint paths between s 1 to t 1 and s 2 to t 2? Iff No encoding nodes are needed to send 2 messages from s to t 1 and t 2. s 1 s 2 t 1 t 2 G 8

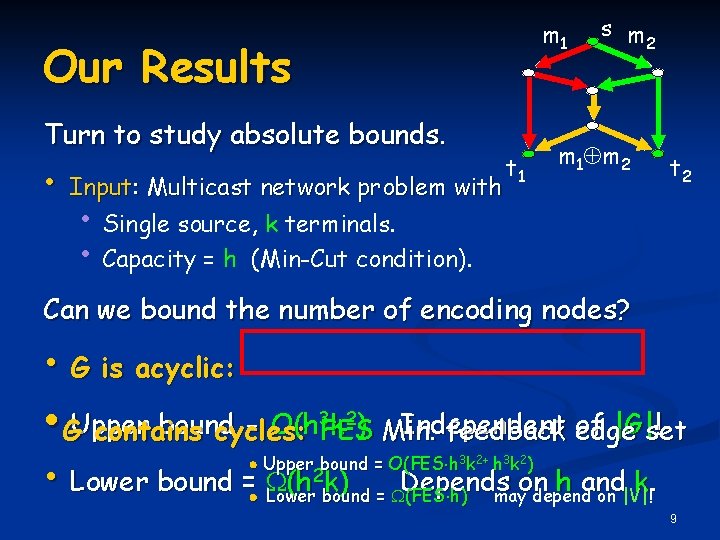
m 1 Our Results Turn to study absolute bounds. • Input: Multicast network problem with t 1 s m 2 m 1 m 2 t 2 • Single source, k terminals. • Capacity = h (Min-Cut condition). Can we bound the number of encoding nodes? • G is acyclic: 3 k 2 ) • • GUpper bound = O(h Independent of |G|set ! contains cycles: FES Min. feedback edge Upper bound = O(FES h k ) • Lower bound = Lower (h 2 bound k) = Depends on h and k. (FES h) may depend on |V|! 3 2+ 3 2 9

s Related work t 1 t 2 Bounds on number of encoding nodes have been considered: • [Fragouli. Soljanin 04]: • [Tavory. Feder. Ron 04]: • Special case in which h=2. • Acyclic: number of encoding nodes ≤ k. • Techniques do not seem to extend to general h. • Partial results: for h=2, other special cases. • Conjecture: universal bound depends on k and h. 10

Upper bound (acyclic networks( • • Theorem: • Multicast of h packets to k destinations requires at most O(h 3 k 2) encoding nodes. Proof Techniques: • Constructive: we construct a network coding scheme. • Combinatorial: we build upon Min-Cut condition. • Analysis: we use tools from theory of network flows. 11

Proof overview: k=2 • Input: Multicast network problem with single source, k=2 terminals, and capacity = h (Min-Cut condition). • • Objective: Coding scheme with O(h 3) encoding nodes. Three steps: • Step 1: Reduce maximal degree of input instance. • Construct new instance with max. degree 3. • Step 2: Discard unnecessary edges. encodinggraph has at most O(h 3) nodes of • Step 3: Remaining in-degree > 1 Any coding scheme will suffice. forwarding 12

Step 1: degree 3 • encoding Input: Multicast network problem with single source, k=2 terminals, and capacity = h (Min-Cut condition). • Step 1: Reduce maximal degree to 3. • Encoding nodes have in-degree >1. 13

encoding Step 3 • • Graph: Max degree 3; h edge disjoint paths between s and t 1 and h disjoint paths between s and t 2; minimal w. r. t. edge removal. Step 3: Prove that number of nodes with in-degree > 1 is O(h 3). We show: every pair of paths intersect in at most h places. • Implies bound of h 3. Proof technique: • • Define h special paths between t 1 and t 2. No three different paths intersect more than once. s t 1 t 2 16

Future research • Seen: bounds on # encoding nodes needed at capacity. • Other aspects of optimization may be considered: • Close gap between upper and lower bound. • Cost on edges for reservation of capacity. 17