The EM algorithm and Fisher vector image representation

The EM algorithm, and Fisher vector image representation Jakob Verbeek December 17, 2010 Course website: http: //lear. inrialpes. fr/~verbeek/MLCR. 10. 11. php

Plan for the course • Session 1, October 1 2010 – Cordelia Schmid: Introduction – Jakob Verbeek: Introduction Machine Learning • Session 2, December 3 2010 – Jakob Verbeek: Clustering with k-means, mixture of Gaussians – Cordelia Schmid: Local invariant features – Student presentation 1: Scale and affine invariant interest point detectors, Mikolajczyk, Schmid, IJCV 2004. • Session 3, December 10 2010 – Cordelia Schmid: Instance-level recognition: efficient search – Student presentation 2: Scalable Recognition with a Vocabulary Tree, Nister and Stewenius, CVPR 2006.

Plan for the course • Session 4, December 17 2010 – Jakob Verbeek: The EM algorithm, and Fisher vector image representation – Cordelia Schmid: Bag-of-features models for category-level classification – Student presentation 2: Beyond bags of features: spatial pyramid matching for recognizing natural scene categories, Lazebnik, Schmid and Ponce, CVPR 2006. • Session 5, January 7 2011 – Jakob Verbeek: Classification 1: generative and non-parameteric methods – Student presentation 4: Large-Scale Image Retrieval with Compressed Fisher Vectors, Perronnin, Liu, Sanchez and Poirier, CVPR 2010. – Cordelia Schmid: Category level localization: Sliding window and shape model – Student presentation 5: Object Detection with Discriminatively Trained Part Based Models, Felzenszwalb, Girshick, Mc. Allester and Ramanan, PAMI 2010. • Session 6, January 14 2011 – Jakob Verbeek: Classification 2: discriminative models – Student presentation 6: Tag. Prop: Discriminative metric learning in nearest neighbor models for image auto-annotation, Guillaumin, Mensink, Verbeek and Schmid, ICCV 2009. – Student presentation 7: IM 2 GPS: estimating geographic information from a single image, Hays and Efros, CVPR 2008.

Clustering with k-means vs. Mo. G • Hard assignment in k-means is not robust near border of quantization cells • Soft assignment in Mo. G accounts for ambiguity in the assignment • Both algorithms sensitive for initialization – Run from several initializations – Keep best result • Nr of clusters need to be set • Both algorithm can be generalized to other types of distances or densities Images from [Gemert et al, IEEE TPAMI, 2010]

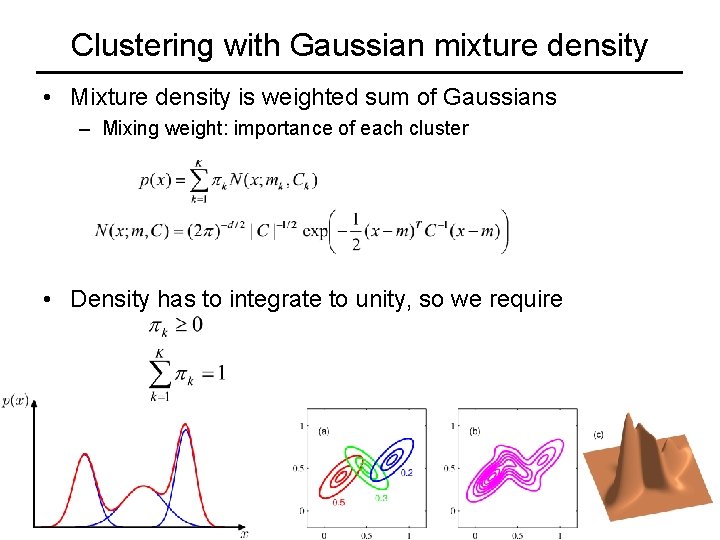
Clustering with Gaussian mixture density • Mixture density is weighted sum of Gaussians – Mixing weight: importance of each cluster • Density has to integrate to unity, so we require

Clustering with Gaussian mixture density • Given: data set of N points xn, n=1, …, N • Find mixture of Gaussians (Mo. G) that best explains data – Parameters: mixing weights, means, covariance matrices – Assume data points are drawn independently – Maximize log-likelihood of data set X w. r. t. parameters • As with k-means objective function has local minima – Can use Expectation-Maximization (EM) algorithm – Similar to the iterative k-means algorithm

Maximum likelihood estimation of Mo. G • Use EM algorithm – – Initialize Mo. G parameters E-step: soft assign of data points to mixture components M-step: update the parameters Repeat EM steps, terminate if converged • Convergence of parameters or assignments • E-step: compute posterior on z given x: • M-step: update parameters using the posteriors

Maximum likelihood estimation of Mo. G • Example of several EM iterations

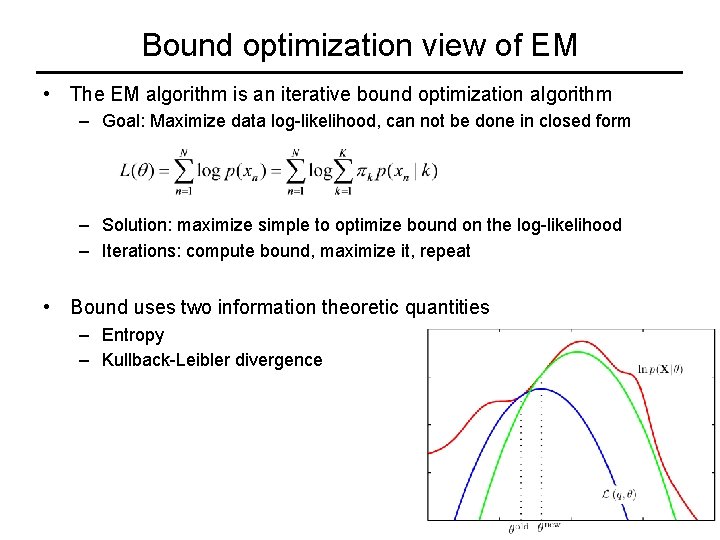
Bound optimization view of EM • The EM algorithm is an iterative bound optimization algorithm – Goal: Maximize data log-likelihood, can not be done in closed form – Solution: maximize simple to optimize bound on the log-likelihood – Iterations: compute bound, maximize it, repeat • Bound uses two information theoretic quantities – Entropy – Kullback-Leibler divergence

Entropy of a distribution • Entropy captures uncertainty in a distribution – Maximum for uniform distribution – Minimum, zero, for delta peak on single value • Connection to information coding (Noiseless coding theorem, Shannon 1948) – Frequent messages short code, optimal code length is (at least) -log p bits – Entropy: expected code length • • Suppose uniform distribution over 8 outcomes: 3 bit code words Suppose distribution: 1/2, 1/4, 1/8, 1/16, 1/64, entropy 2 bits! Code words: 0, 110, 111100, 111101, 111110, 111111 Codewords are “self-delimiting”: – code is of length 6 and starts with 4 ones, or stops after first 0. Low entropy High entropy

Kullback-Leibler divergence • Asymmetric dissimilarity between distributions – Minimum, zero, if distributions are equal – Maximum, infinity, if p has a zero where q is non-zero • Interpretation in coding theory – Sub-optimality when messages distributed according to q, but coding with codeword lengths derived from p – Difference of expected code lengths – – – Suppose distribution q: 1/2, 1/4, 1/8, 1/16, 1/64, 1/64 Coding with uniform 3 -bit code, p=uniform Expected code length using p: 3 bits Optimal expected code length, entropy H(q) = 2 bits KL divergence D(q|p) = 1 bit

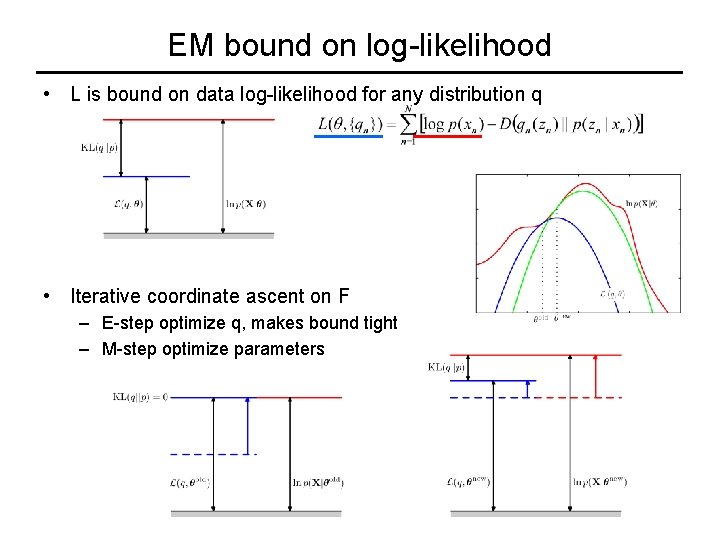
EM bound on log-likelihood • Define Gauss. mixture p(x) as marginal distribution of p(x, z) • Posterior distribution on latent cluster assignment • Let qn(zn) be arbitrary distribution over cluster assignment • Bound log-likelihood by subtracting KL divergence D(q(z) || p(z|x))

Maximizing the EM bound on log-likelihood • E-step: fix model parameters, update distributions qn – KL divergence zero if distributions are equal – Thus set qn(zn) = p(zn|xn) • M-step: fix the qn, update model parameters • Terms for each Gaussian decoupled from rest !

Maximizing the EM bound on log-likelihood • Derive the optimal values for the mixing weights – Maximize – Take into account that weights sum to one, define – Take derivative for mixing weight k>1

Maximizing the EM bound on log-likelihood • Derive the optimal values for the Mo. G parameters – Maximize

EM bound on log-likelihood • L is bound on data log-likelihood for any distribution q • Iterative coordinate ascent on F – E-step optimize q, makes bound tight – M-step optimize parameters

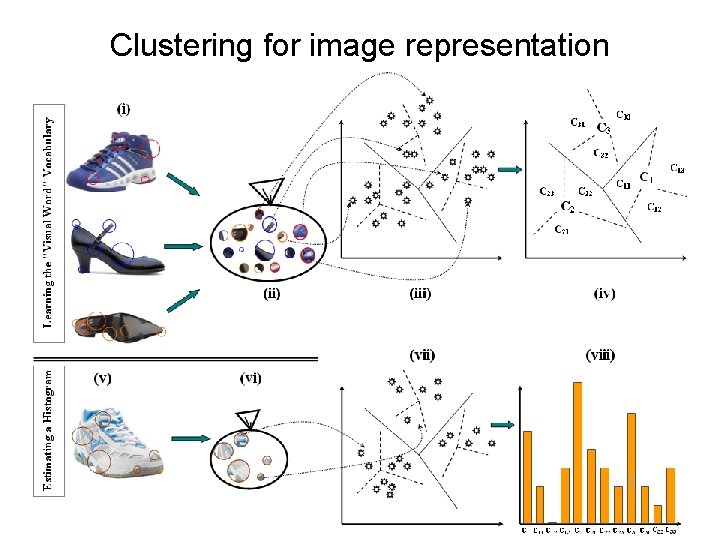
Clustering for image representation • For each image that we want to classify / analyze 1. Detect local image regions – For example affine invariant interest points 2. Describe the appearance of each region – For example using the SIFT decriptor 3. Quantization of local image descriptors – using k-means or mixture of Gaussians – (Soft) assign each region to clusters – Count how many regions were assigned to each cluster • Results in a histogram of (soft) counts – – How many image regions were assigned to each cluster Input to image classification method • Off-line: learn k-means quantization or mixture of Gaussians from data of many images

Clustering for image representation • Detect local image regions – For example affine invariant interest points • Describe the appearance of each region – For example using the SIFT decriptor • Quantization of local image descriptors – – using k-means or mixture of Gaussians Cluster centers / Gaussians learned off-line (Soft) assign each region to clusters Count how many regions were assigned to each cluster • Results in a histogram of (soft) counts – How many image regions were assigned to each cluster • Input to image classification method

Fisher vector representation: motivation • Feature vector quantization is computationally expensive in practice • Run-time linear in – N: nr. of feature vectors ~ 10^3 per image – D: nr. of dimensions ~ 10^2 (SIFT) – K: nr. of clusters ~ 10^3 for recognition • So in total in the order of 10^8 multiplications per image to obtain a histogram of size 1000 • Can we do this more efficiently ? ! – Yes, store more than the number of data points assigned to each cluster centre / Gaussian 20 10 • Reading material: “Fisher Kernels on Visual Vocabularies for Image Categorization” F. Perronnin and C. Dance, in CVPR'07 Xerox Research Centre Europe, Grenoble 5 3 8

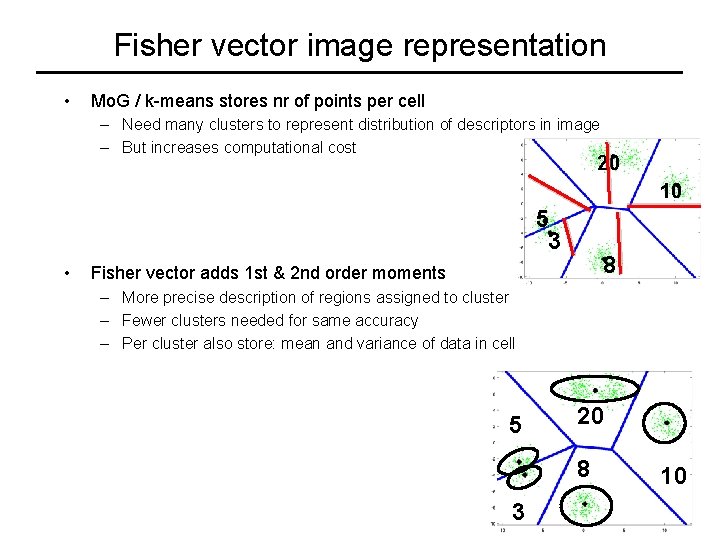
Fisher vector image representation • Mo. G / k-means stores nr of points per cell – Need many clusters to represent distribution of descriptors in image – But increases computational cost 20 10 5 3 • 8 Fisher vector adds 1 st & 2 nd order moments – More precise description of regions assigned to cluster – Fewer clusters needed for same accuracy – Per cluster also store: mean and variance of data in cell 5 20 8 3 10

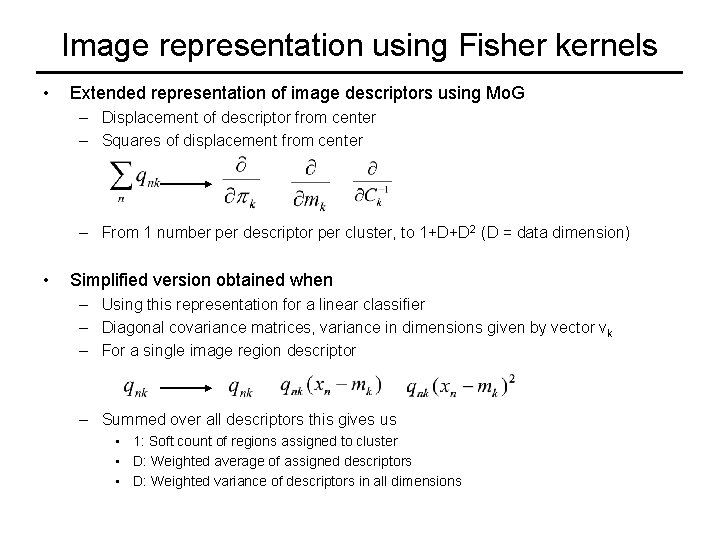
Image representation using Fisher kernels • General idea of Fischer vector representation – Fit probabilistic model to data – Use derivative of data log-likelihood as data representation, eg. for classification See [Jaakkola & Haussler. “Exploiting generative models in discriminative classifiers”, in Advances in Neural Information Processing Systems 11, 1999. ] • Here, we use Mixture of Gaussians to cluster the region descriptors • Concatenate derivatives to obtain data representation

Image representation using Fisher kernels • Extended representation of image descriptors using Mo. G – Displacement of descriptor from center – Squares of displacement from center – From 1 number per descriptor per cluster, to 1+D+D 2 (D = data dimension) • Simplified version obtained when – Using this representation for a linear classifier – Diagonal covariance matrices, variance in dimensions given by vector vk – For a single image region descriptor – Summed over all descriptors this gives us • 1: Soft count of regions assigned to cluster • D: Weighted average of assigned descriptors • D: Weighted variance of descriptors in all dimensions

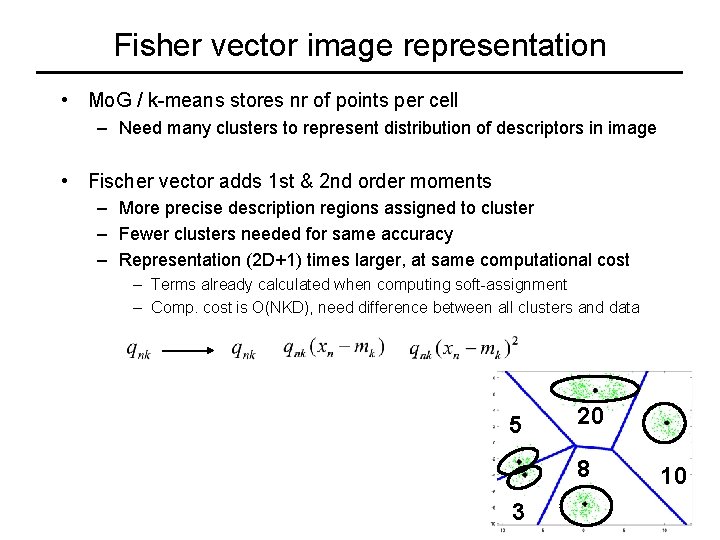
Fisher vector image representation • Mo. G / k-means stores nr of points per cell – Need many clusters to represent distribution of descriptors in image • Fischer vector adds 1 st & 2 nd order moments – More precise description regions assigned to cluster – Fewer clusters needed for same accuracy – Representation (2 D+1) times larger, at same computational cost – Terms already calculated when computing soft-assignment – Comp. cost is O(NKD), need difference between all clusters and data 5 20 8 3 10

Images from categorization task PASCAL VOC • Yearly “competition” since 2005 for image classification (also object localization, segmentation, and body-part localization)

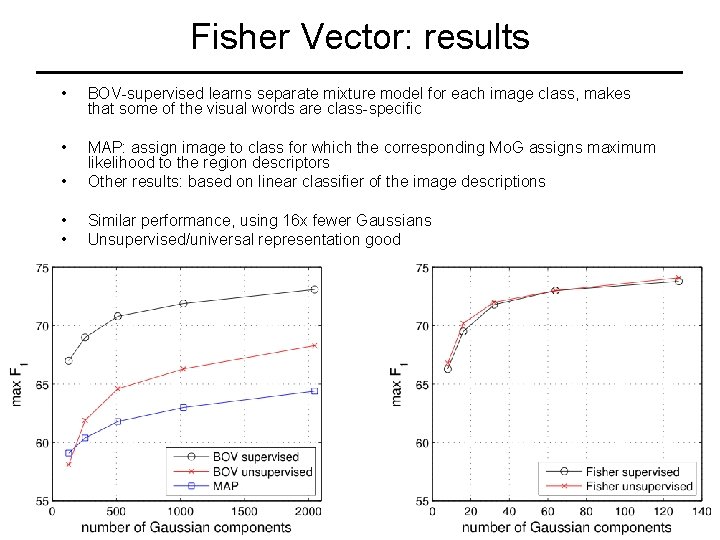
Fisher Vector: results • BOV-supervised learns separate mixture model for each image class, makes that some of the visual words are class-specific • • MAP: assign image to class for which the corresponding Mo. G assigns maximum likelihood to the region descriptors Other results: based on linear classifier of the image descriptions • • Similar performance, using 16 x fewer Gaussians Unsupervised/universal representation good

How to set the nr of clusters? • Optimization criterion of k-means and Mo. G always improved by adding more clusters – K-means: min distance to closest cluster can not increase by adding a cluster center – Mo. G: can always add the new Gaussian with zero mixing weight, (k+1) component models contain k component models. • Optimization criterion cannot be used to select # clusters • Model selection by adding penalty term increasing with # clusters – Minimum description length (MDL) principle – Bayesian information criterion (BIC) – Aikaike informaiton criterion (AIC) • Cross-validation if used for another task, eg. Image categorization – check performance of final system on validation set of labeled images • For more details see “Pattern Recognition & Machine Learning”, by C. Bishop, 2006. In particular chapter 9, and section 3. 4

How to set the nr of clusters? • Bayesian model that treats parameters as missing values – Prior distribution over parameters – Likelihood of data given by averaging over parameter values • Variational Bayesian inference for various nr of clusters – Approximate data log-likelihood using the EM bound – E-step: distribution q generally too complex to represent exact – Use factorizing distribution q, not exact, KL divergence > 0 • For models with – Many parameters: fits many data sets – Few parameters: won’t fit data well – The “right” nr. of parameters: good fit Data sets