The Electronic Spectra of Coordination Compounds The UVVis

The Electronic Spectra of Coordination Compounds

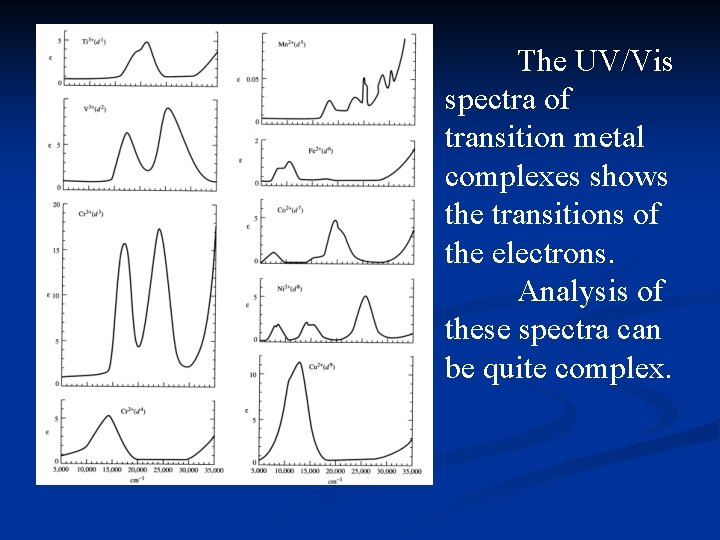
The UV/Vis spectra of transition metal complexes shows the transitions of the electrons. Analysis of these spectra can be quite complex.

Electron Spectra The UV/Vis spectra are used to determine the value of ∆o for the complex. The spectra arise from electronic transitions between the t 2 g and eg sets if molecular orbitals. Electronelectron interactions can greatly complicate the spectra. Only in the case of a single electron is interpretation of the spectrum straightforward.

Obtaining ∆o For a d 1 configuration, only a single peak is seen. It results from the electron promotion from the t 2 g orbitals to the eg orbitals. The “toothed” appearance of the peak is due to a Jahn-Teller distortion of the excited state. The energy of the peak = ∆o.

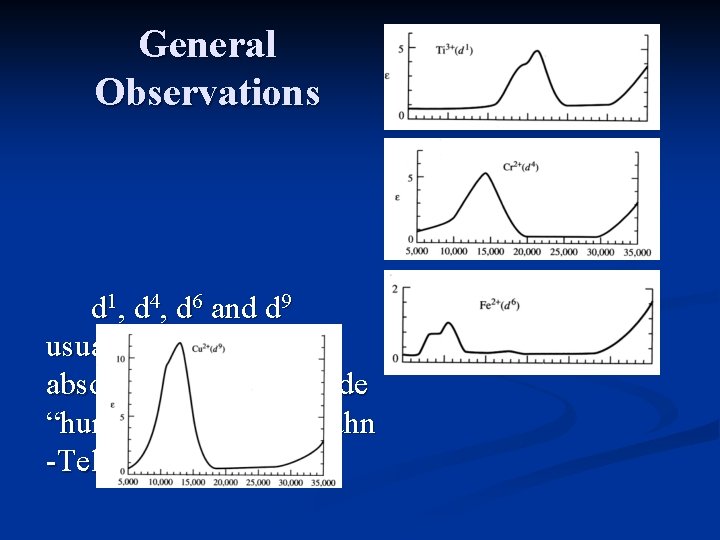
General Observations d 1, d 4, d 6 and d 9 usually have 1 absorption, though a side “hump” results from Jahn -Teller distortions.

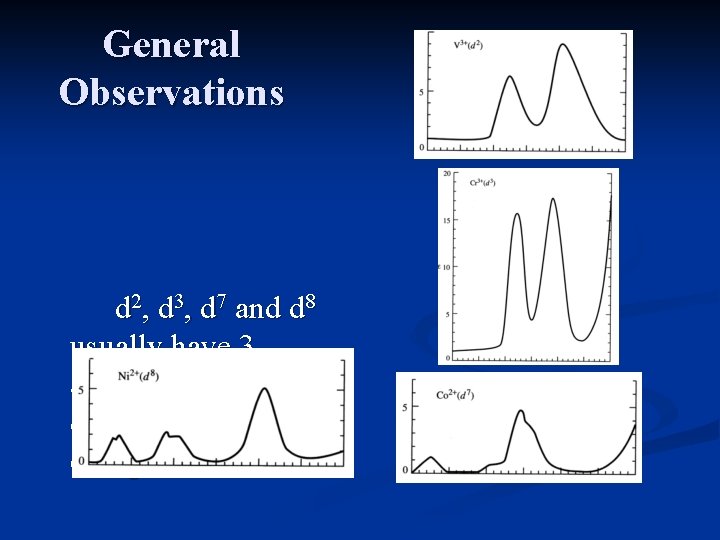
General Observations d 2, d 3, d 7 and d 8 usually have 3 absorptions, one is often obscured by a charge transfer band.

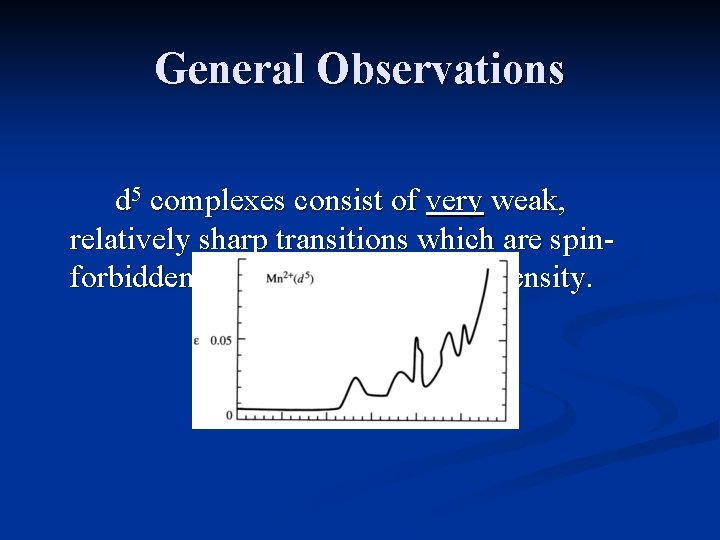
General Observations d 5 complexes consist of very weak, relatively sharp transitions which are spinforbidden, and have a very low intensity.

Qualitative Explanation Consider a Cr(III) complex such as [Cr(NH 3)6]3+. The ground state configuration is: ____ A transition from the dz 2 dx 2 -y 2 dxy to the dx 2 -y 2, or the dyz or dxz to the dz 2 ____ orbitals involve a relatively dxy dyz dxz minor change in environment.

Qualitative Explanation The transition from the dxz orbitals to the dz 2 orbitals involves a relatively minor change in the electronic environment.

Qualitative Explanation Consider a Cr(III) complex such as [Cr(NH 3)6]3+. The ground state configuration is: ____ A transition from the dz 2 dx 2 -y 2 dxy to the dz 2, or the dyz or dxz to the dx 2 -y 2 ____ orbitals involve a major dxy dyz dxz change in environment.

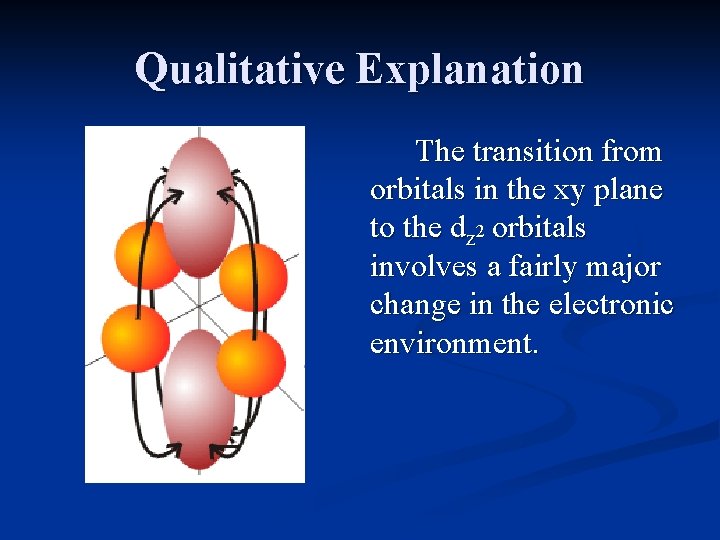
Qualitative Explanation The transition from orbitals in the xy plane to the dz 2 orbitals involves a fairly major change in the electronic environment.

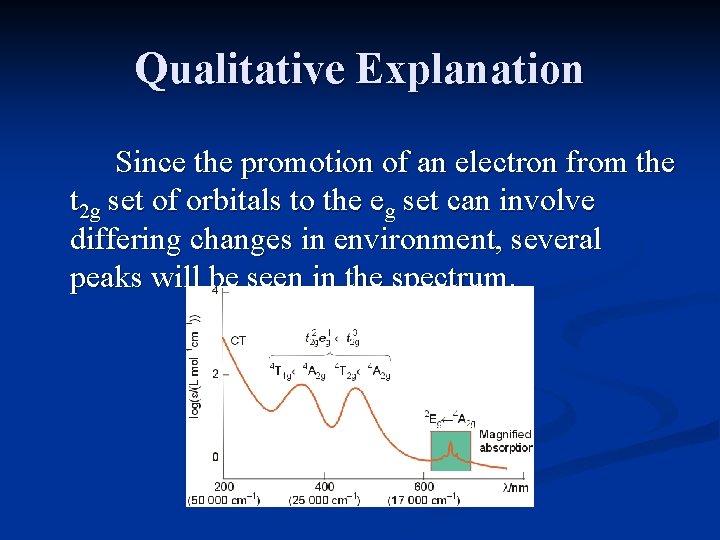
Qualitative Explanation Since the promotion of an electron from the t 2 g set of orbitals to the eg set can involve differing changes in environment, several peaks will be seen in the spectrum.

3 d Multi-electron Complexes For complexes with more than one electron in the 3 d (and 4 s) orbitals of the metal, electron interactions must be considered. The electrons are not independent of each other, and the orbital angular momenta (ml values) and the spin angular momenta (ms values) interact.

4 d and 5 d Metal Complexes The lower transition metals undergo further coupling (called j-j coupling or spin-orbit coupling).

3 d Multi-electron Complexes The interaction is called Russel-Saunders or L-S coupling. The interactions produce atomic states called microstates that are described by a new set of quantum numbers. ML = total orbital angular momentum =Σml MS = total spin angular momentum = Σms

Determining the Energy States of an Atom A microstate table that contains all possible combinations of ml and ms is constructed. Each microstate represents a possible electron configuration. Both ground state and excited states are considered.

Energy States Microstates would have the same energy only if repulsion between electrons is negligible. In an octahedral or tetrahedral complex, microstates that correspond to different relative spatial distributions of the electrons will have different energies. As a result, distinguishable energy levels, called terms are seen.

Energy States To obtain all of the terms for a given electron configuration, a microstate table is constructed. The table is a grid of all possible electronic arrangements. It lists all of the possible values of spin and orbital orientation. It includes both ground and excited states, and must obey the Pauli Exclusion Principle.

Constructing a Microstate Table Consider an atom of carbon. Its highest occupied orbital has a p 2 electron configuration. Microstates correspond to the various possible occupation of the px, py and pz orbitals.

Constructing a Microstate Table ml = +1 0 -1 Configurations: ___ ___ ___ microstate: (1+, 0+) (0+, -1+) (1+, -1+) These are examples of some of the ground state microstates. Others would have the electrons (arrows) pointing down.

Constructing a Microstate Table ml = +1 0 -1 Configurations: ___ ___ ___ microstate: (1+, 1 -) (0+, 0 -) (-1+, -1 -) These are examples of some of the excited state microstates.

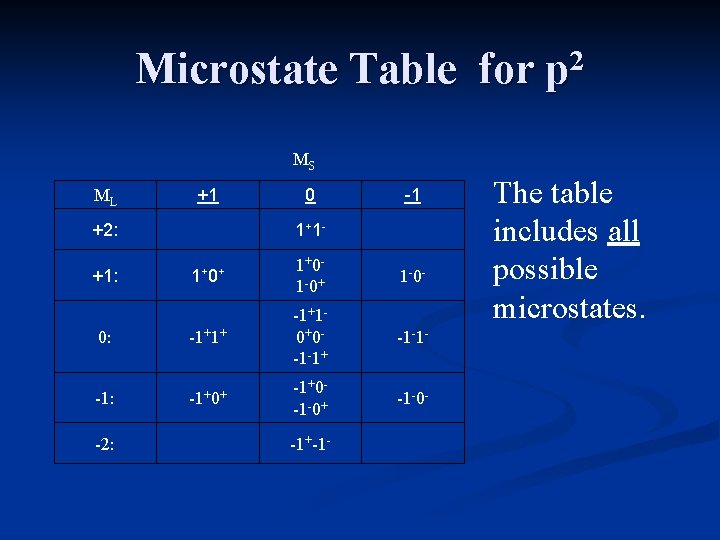
Microstate Table for p 2 For the carbon atom, ML will range from +2 down to -2, and MS can have values of +1 (both electrons “pointing up”), 0 (one electron “up”, one electron “down), or -1 (both electrons “pointing down”).

Microstate Notation For the carbon atom, ML will range from +2 down to -2, and MS can have values of +1 (both electrons “pointing up”), 0 (one electron “up”, one electron “down), or -1 (both electrons “pointing down”).

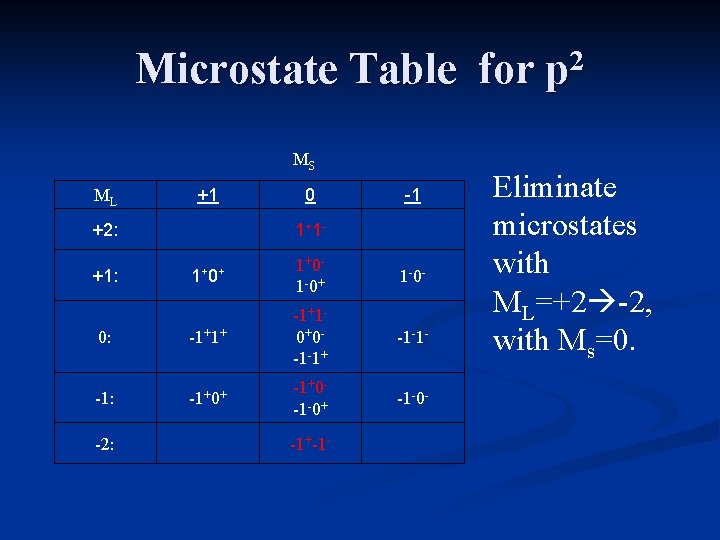
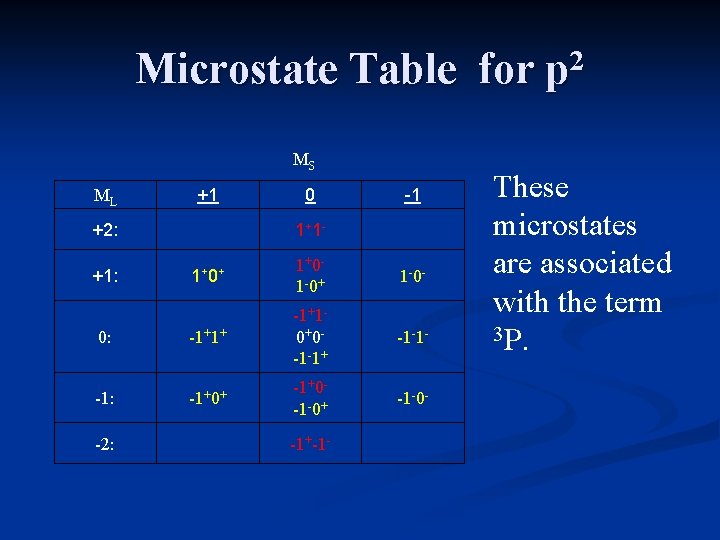
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - The table includes all possible microstates.

Constructing a Microstate Table Once the microstate table is complete, the microstates are collected or grouped into atomic (coupled) energy states.

Constructing a Microstate Table For two electrons, L = l 1+ l 2, l 1+ l 2 -1, l 1+ l 2 -2, …│l 1 - l 2│ For a p 2 configuration, L = 1+1, 1+1 -1, 1 -1. The values of L are: 2, 1 and 0. L is always positive, and ranges from the maximum value of Σl.

Constructing a Microstate Table For two electrons, S = s 1+ s 2, s 1+ s 2 -1, s 1+ s 2 -2, …│s 1 - s 2│ For a p 2 configuration, S = ½ + ½ , ½ + ½ -1. The values of S are: 1 and 0.

Atomic Quantum Numbers Quantum numbers L and S describe collections of microstates, whereas ML and MS describe the individual microstates themselves.

Constructing a Microstate Table The microstate table is a grid that includes all possible combinations of L, the total angular momentum quantum number, and S, the total spin angular momentum quantum number. For two electrons, L = l 1+ l 2, l 1+ l 2 -1, l 1+ l 2 -2, …│l 1 - l 2│ S = s 1+ s 2, s 1+ s 2 -1, s 1+ s 2 -2, …│s 1 - s 2│

Constructing a Microstate Table Once the microstate table is complete, all microstates associated with an energy state with specific value of L and S are grouped. It doesn’t matter which specific microstates are placed in the group. Microstates are grouped and eliminated until all microstates are associated with a specific energy state or term.

Term Symbols Each energy state or term is represented by a term symbol. The term symbol is a capitol letter that is related to the value of L. L = 0 1 2 3 4 Term Symbol S P D F G

Term Symbols The upper left corner of the term symbol contains a number called the multiplicity. The multiplicity is the number of unpaired electrons +1, or 2 S+1.

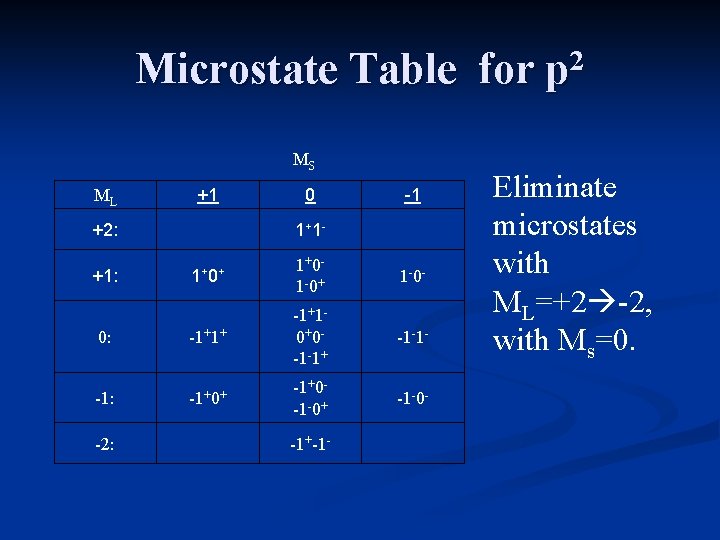
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+2 -2, with Ms=0.

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+2 -2, with Ms=0.

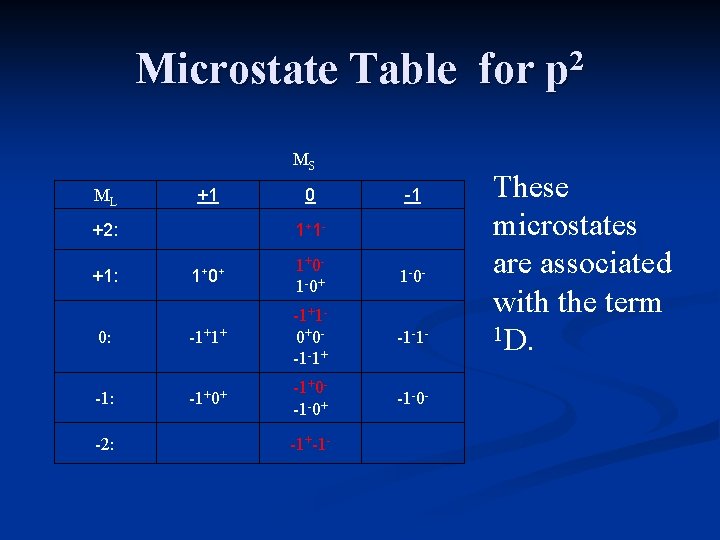
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - These microstates are associated with the term 1 D.

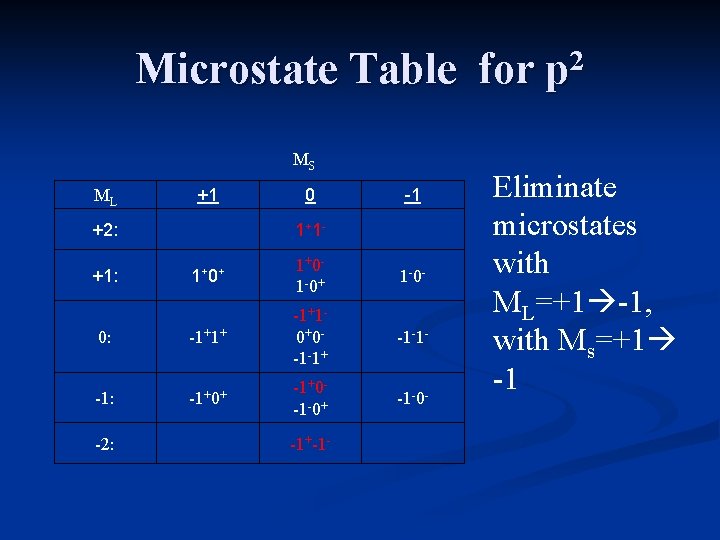
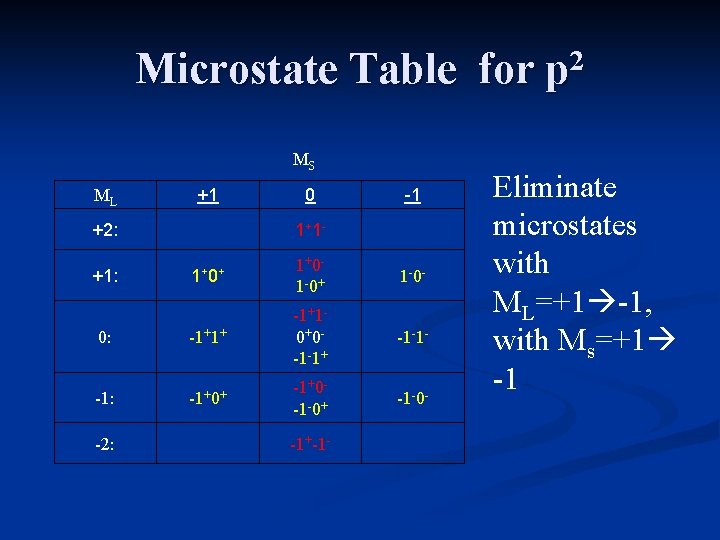
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+1 -1, with Ms=+1 -1

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+1 -1, with Ms=+1 -1

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - These microstates are associated with the term 3 P.

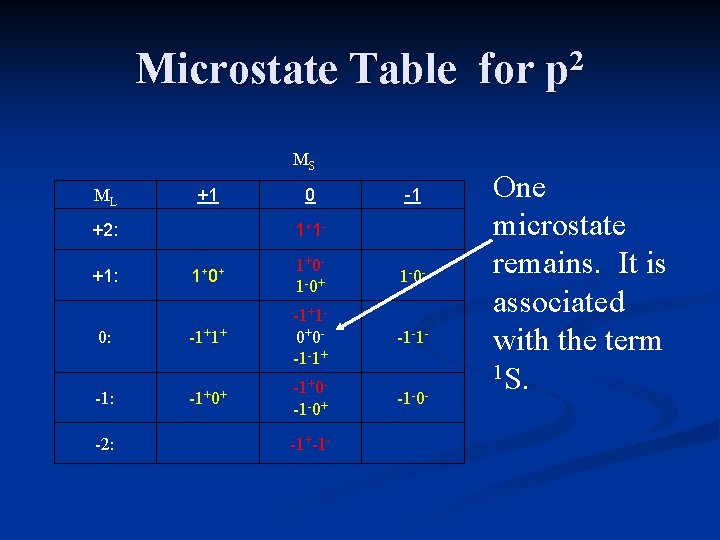
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - One microstate remains. It is associated with the term 1 S.

Term States for p 2 The term states for a p 2 electron configuration are 1 S, 3 P, and 1 D. The term symbol with the greatest multiplicity and highest value of ML will be the ground state. 3 P is the ground state term for carbon.

Determining the Relative Energy of Term States 1. For a given electron configuration, the term with the greatest multiplicity lies lowest in energy. (This is consistent with Hund’s rule. ) 2. For a term of a given multiplicity, the greater the value of L, the lower the energy.

Determining the Relative Energy of Term States For a p 2 configuration, the term states are 3 P, 1 D and 1 S. The terms for the free atom should have the following relative energies: 3 P< 1 D <1 S

Determining the Relative Energy of Term States The rules for predicting the ground state always work, but they may fail in predicting the order of energies for excited states.

Energy States for a d 2 Configuration A microstate table for a d 2 electron configuration will contain 45 microstates (ML = 4 -4, and MS=1, 0 or -1) associated with the following terms: 1 S, 1 D, 1 G, 3 P, and 3 F

Energy States for a d 2 Configuration n Problem: Determine the ground state of a free atom with a d 2 electron configuration, and place the terms in order of increasing energy. 1 S, 1 D, 1 G, 3 P, and 3 F

Determining the Ground State Term We only need to know the ground state term to interpret the spectra of transition metal complexes. This can be obtained without constructing a microstate table. The ground state will a) have the maximum multiplicity b) have the maximum value of ML for the configuration obtained in part (a).

The Splitting of Terms In an octahedral field, the free ion terms will split due to their differing spatial orientations. Term S P D F G # of States Terms in Oh Field 1 A 1 g 3 T 1 g 5 T 2 g + Eg 7 T 1 g + T 2 g + A 2 g 9 A 1 g + Eg+T 1 g+T 2 g

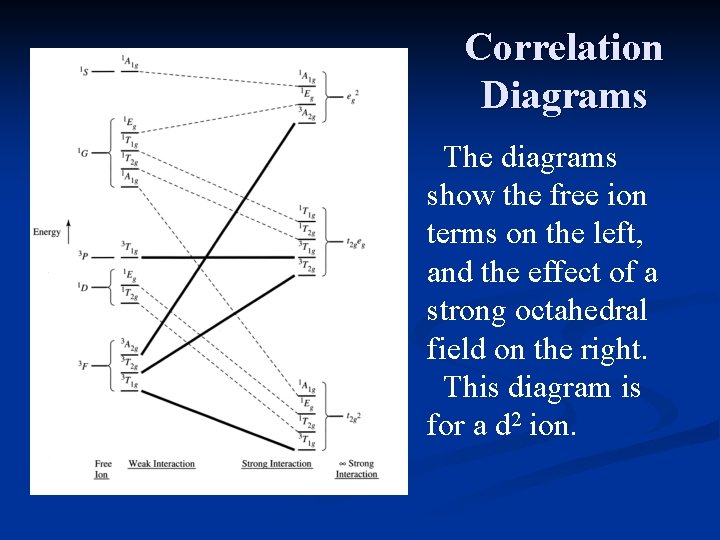
Correlation Diagrams The diagrams show the free ion terms on the left, and the effect of a strong octahedral field on the right. This diagram is for a d 2 ion.

Correlation Diagrams The terms converge on the right side of the diagram in three clusters. Each of these represents the possible electron configurations for a d 2 ion in a strong octahedral field.

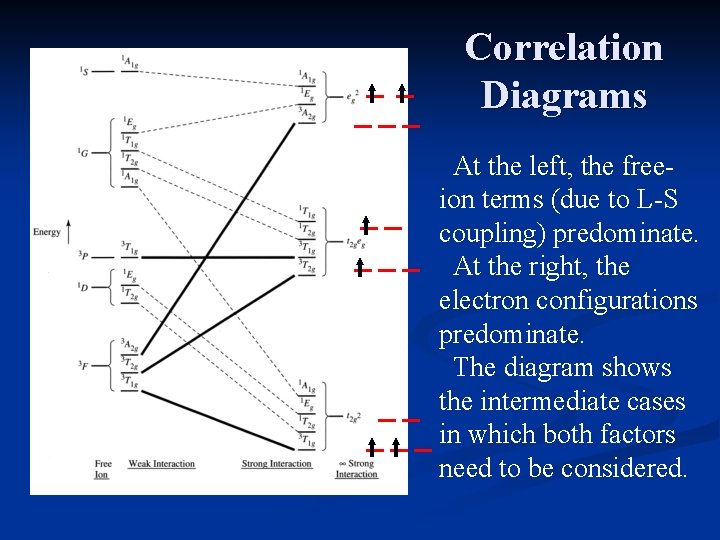
Correlation Diagrams At the left, the freeion terms (due to L-S coupling) predominate. At the right, the electron configurations predominate. The diagram shows the intermediate cases in which both factors need to be considered.

Correlation Diagrams This correlation diagram shows the ground state and spinallowed transitions in bold lines.

Selection Rules There are several selection rules that govern the intensities of the absorption bands seen in transition metal complexes. 1. Transitions between states of the same parity (g g or u u) are forbidden. This is the Laporte Rule. This rule would forbid electronic transitions between d orbitals, since all d orbitals are gerade.

Selection Rules 1. Transitions between states of the same parity (g g or u u) are forbidden. This is the Laporte Rule. This rule is relaxed due to vibrations of the complex that cause a loss of the center of symmetry. As a result, molar absorbitivities of 10 -50 L/mol-cm are observed.

Selection Rules 2. Transitions between states of different multiplicities are forbidden. This is called the spin selection rule. This rule can be relaxed very slightly for the first row transition metals by spin-orbit coupling. Typical molar absorbitivities are less than 1 L/mol-cm, with very pale color observed.

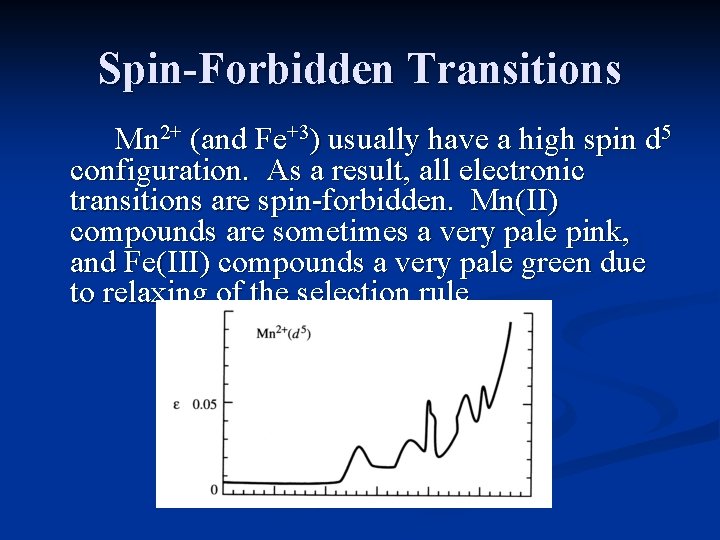
Spin-Forbidden Transitions Mn 2+ (and Fe+3) usually have a high spin d 5 configuration. As a result, all electronic transitions are spin-forbidden. Mn(II) compounds are sometimes a very pale pink, and Fe(III) compounds a very pale green due to relaxing of the selection rule.

Correlation Diagrams This diagram shows the possible transitions that do not violate the spin selection rule. A d 2 complex should have 3 possible transitions.

Correlation Diagrams A non-crossing rule is observed in correlation diagrams. Terms or energy states of the same symmetry interact so that their energies never cross.

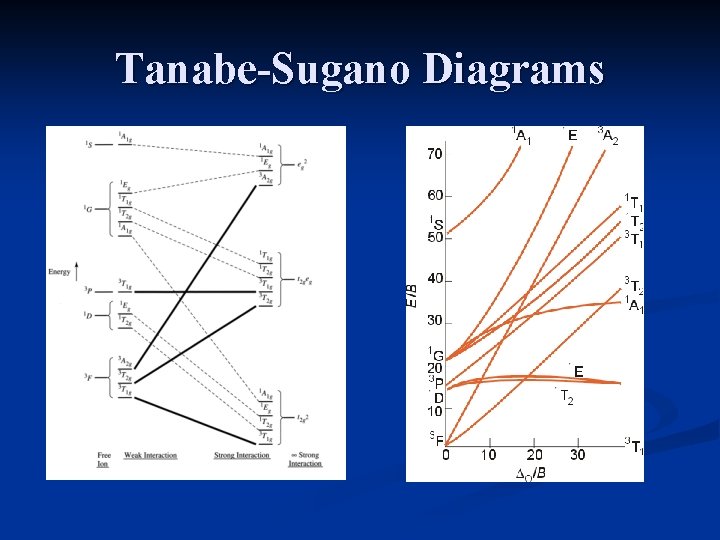
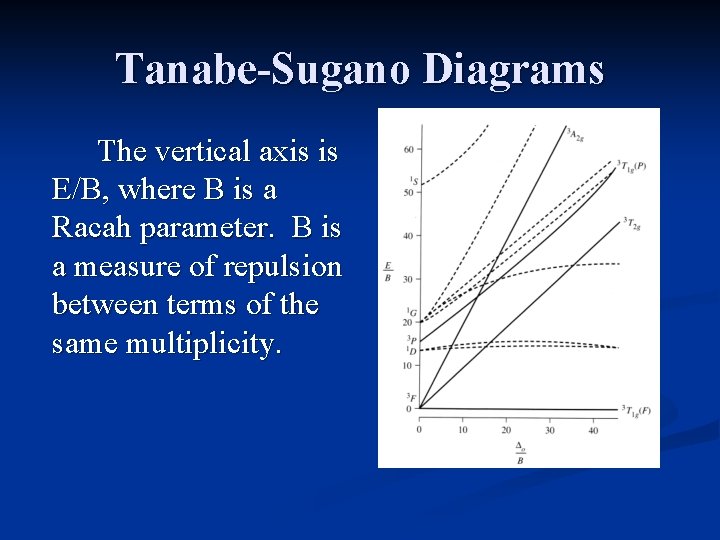
Tanabe-Sugano Diagrams In order to accurately interpret the electronic spectra of transition metal complexes, a series of diagrams have been created. These diagrams are used to assign transitions (initial energy state and final energy state) to peaks observed in the spectra, and to calculate the value of ∆o.

Tanabe-Sugano Diagrams Tanabe-Sugano diagrams have the lowest energy state (the ground state) plotted along the horizontal axis. The energy of excited states can then be readily compared to the ground state.

Tanabe-Sugano Diagrams

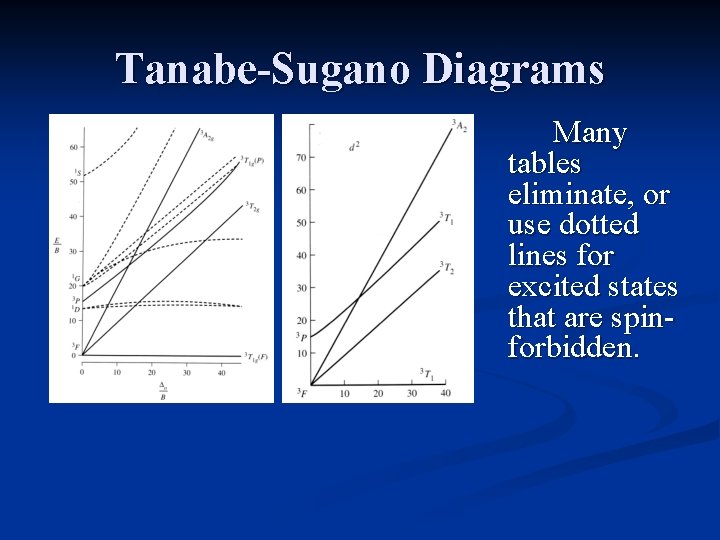
Tanabe-Sugano Diagrams Many tables eliminate, or use dotted lines for excited states that are spinforbidden.

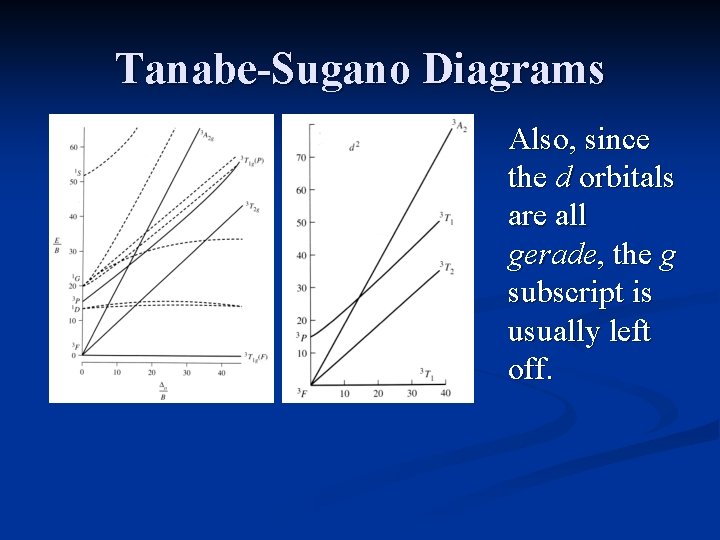
Tanabe-Sugano Diagrams Also, since the d orbitals are all gerade, the g subscript is usually left off.

Tanabe-Sugano Diagrams The vertical axis is E/B, where B is a Racah parameter. B is a measure of repulsion between terms of the same multiplicity.

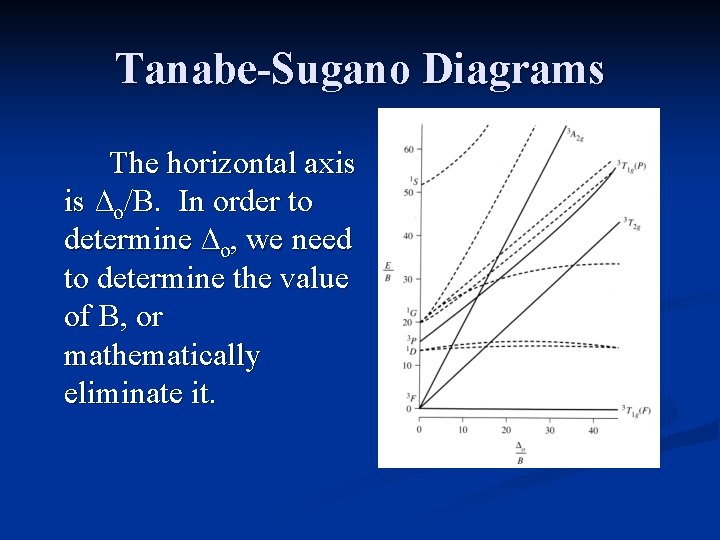
Tanabe-Sugano Diagrams The horizontal axis is ∆o/B. In order to determine ∆o, we need to determine the value of B, or mathematically eliminate it.

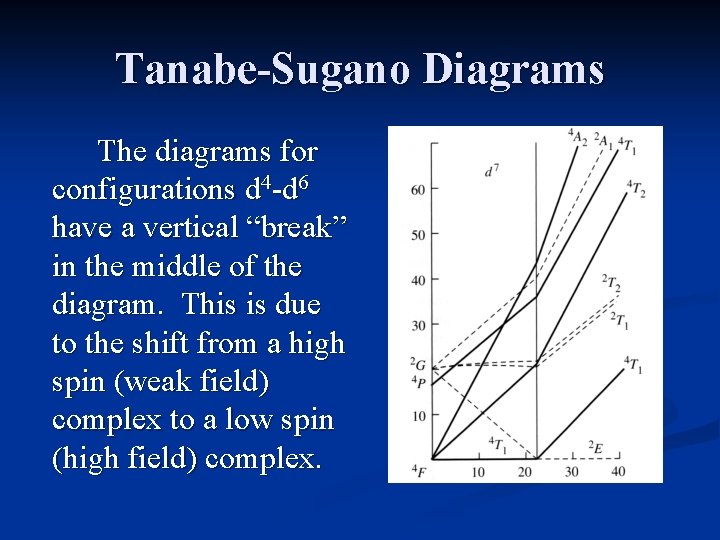
Tanabe-Sugano Diagrams The diagrams for configurations d 4 -d 6 have a vertical “break” in the middle of the diagram. This is due to the shift from a high spin (weak field) complex to a low spin (high field) complex.

Symmetry Labels and Electron Configurations At the far right side of the diagrams, at an infinitely strong octahedral field, the symmetry labels correspond to the electron configuration of the complex. T designates a triply degenerate asymmetrically occupied state. or

Symmetry Labels and Electron Configurations An E label designates a doubly degenerate asymmetrically occupied state. or An A or B label designates a nondegenerate state. or

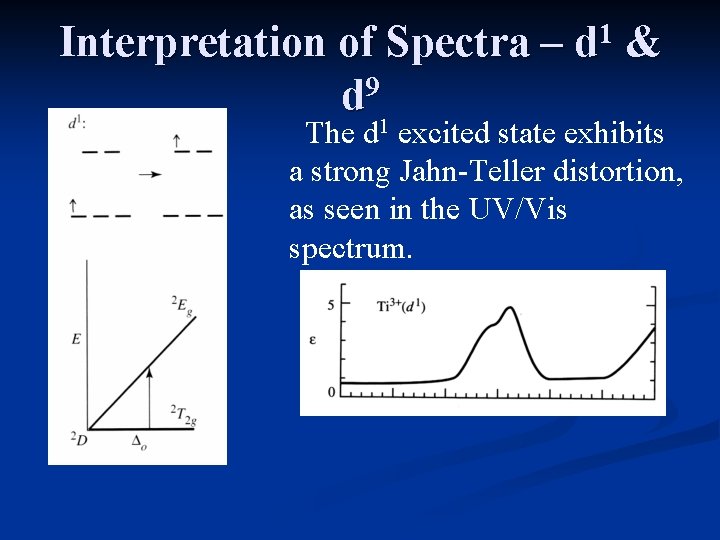
Interpretation of Spectra – 9 d 1 d & There is only 1 spin-allowed transition, with the energy absorbed equal to the value of ∆o.

Interpretation of Spectra – 9 d 1 1 d & The d excited state exhibits a strong Jahn-Teller distortion, as seen in the UV/Vis spectrum.

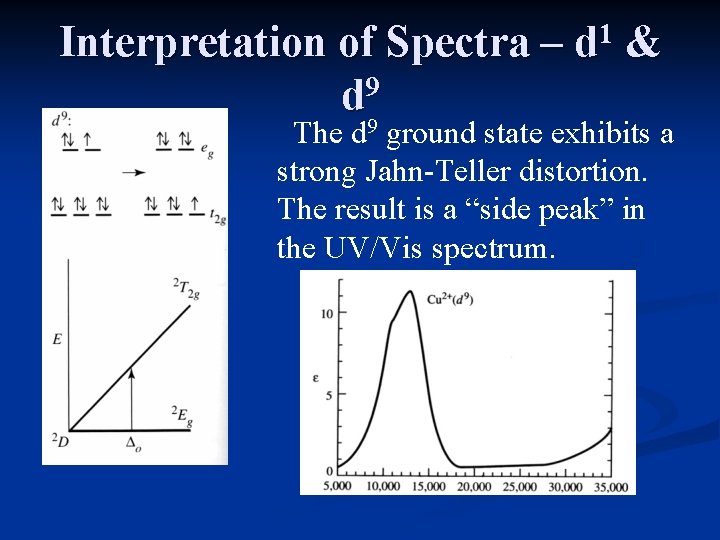
Interpretation of Spectra – 9 d 9 1 d & The d ground state exhibits a strong Jahn-Teller distortion. The result is a “side peak” in the UV/Vis spectrum.

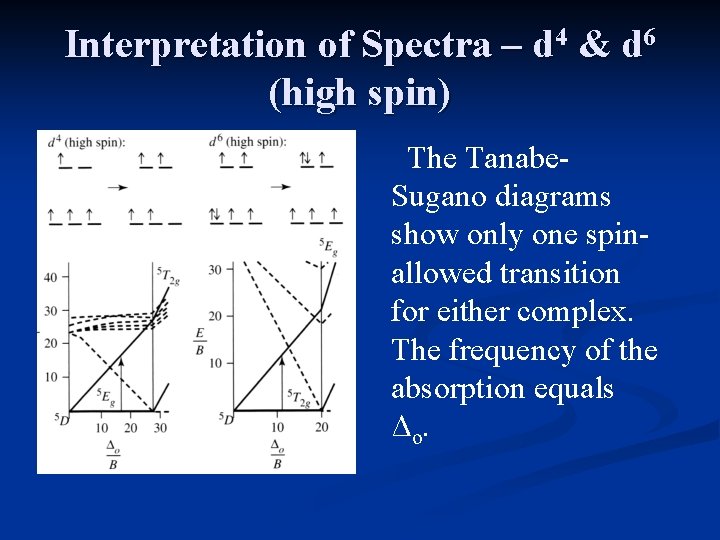
Interpretation of Spectra – d 4 & d 6 (high spin) The Tanabe. Sugano diagrams show only one spinallowed transition for either complex. The frequency of the absorption equals Δo.

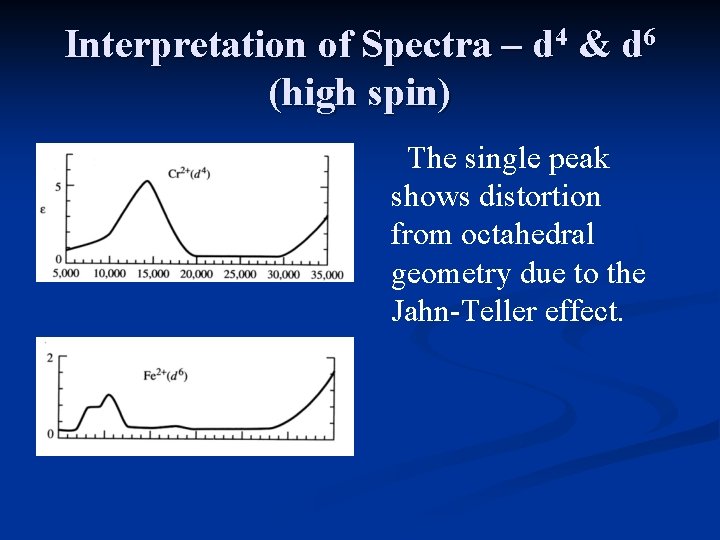
Interpretation of Spectra – d 4 & d 6 (high spin) The single peak shows distortion from octahedral geometry due to the Jahn-Teller effect.

Interpretation of Spectra – d 4 & d 6 (high spin) The ground state of Cr 2+ (d 4) and the excited state of Fe 2+ (d 6) should exhibit strong Jahn. Teller distortions.

Interpretation of Spectra – 8 d 3 d & For a d 3 ground state, the first transition, from 4 A 2 g(F) to 4 T (F) corresponds to ∆. 2 g o LFSE =. 6Δo-. 8 Δo = -. 2 Δo ∆o LFSE = -1. 2 Δo

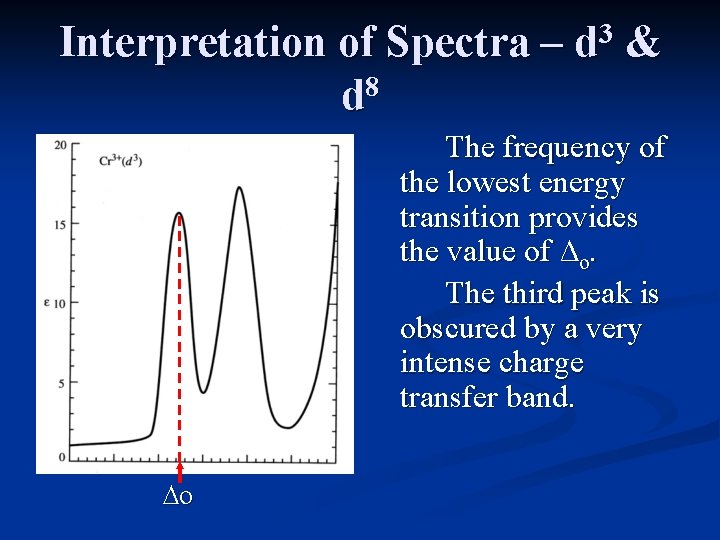
Interpretation of Spectra – 8 d 3 d & The frequency of the lowest energy transition provides the value of ∆o. The third peak is obscured by a very intense charge transfer band. ∆o

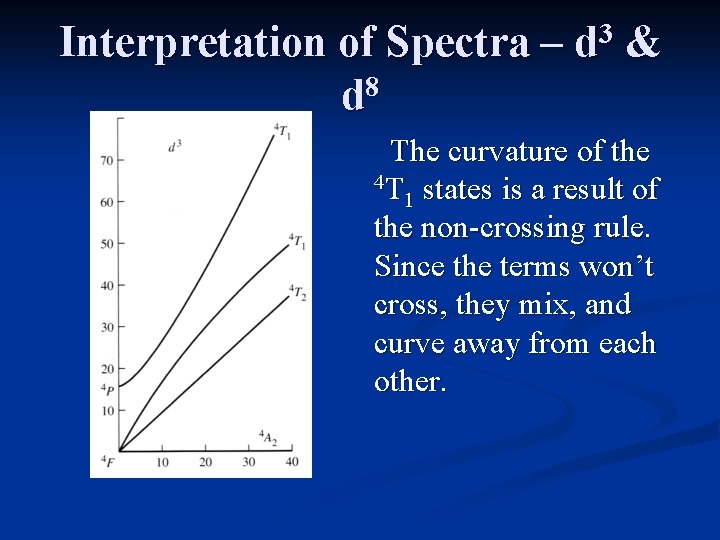
Interpretation of Spectra – 8 d 3 d & The curvature of the 4 T states is a result of 1 the non-crossing rule. Since the terms won’t cross, they mix, and curve away from each other.

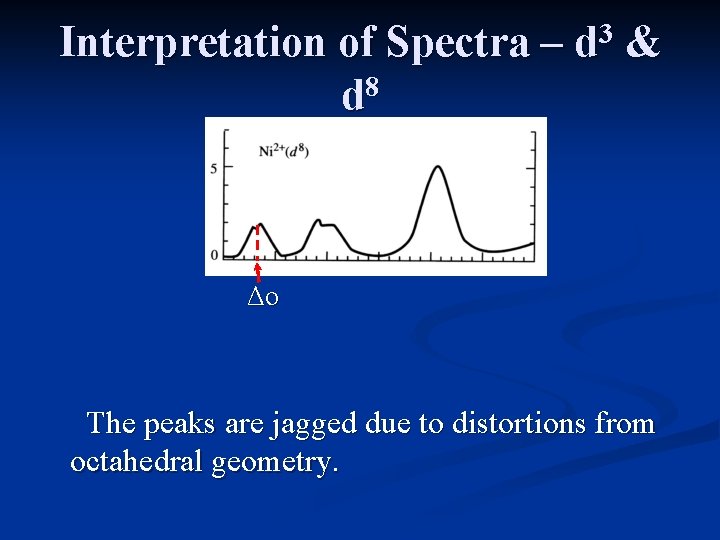
Interpretation of Spectra – 8 d 3 d & The Tanabe-Sugano diagram for d 8 is the same as that for d 3, except the multiplicity is different. Three peaks are expected, with the lowest energy absorption equal to Δo.

Interpretation of Spectra – 8 d 3 d & Δo The peaks are jagged due to distortions from octahedral geometry.

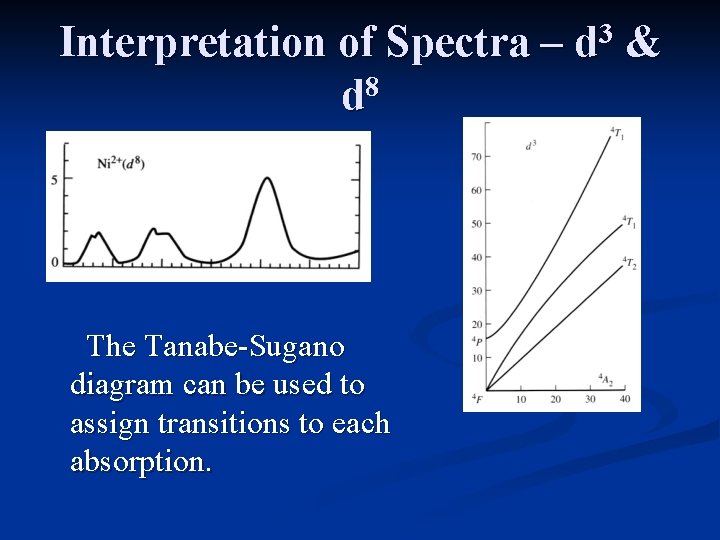
Interpretation of Spectra – 8 d The Tanabe-Sugano diagram can be used to assign transitions to each absorption. 3 d &

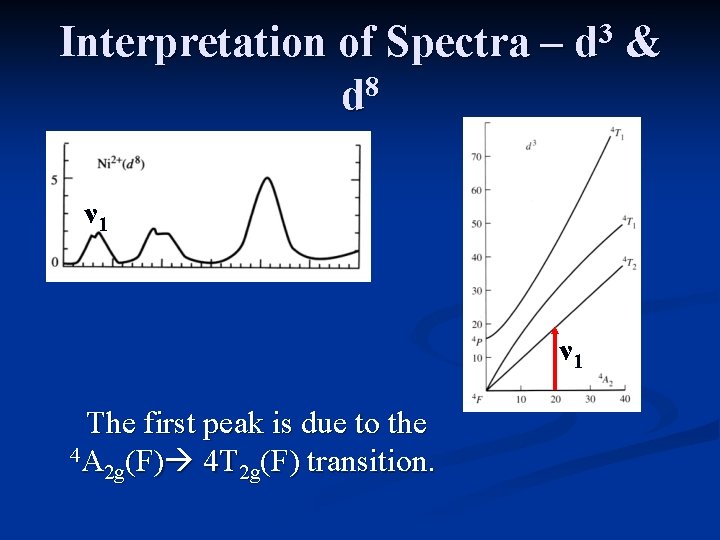
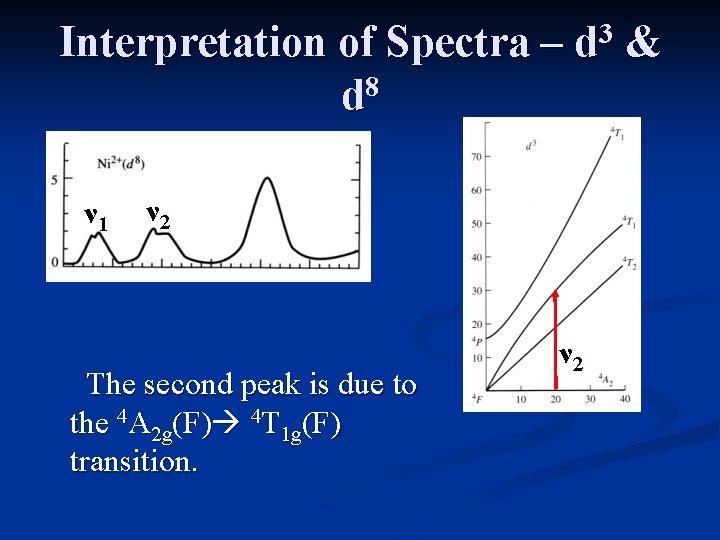
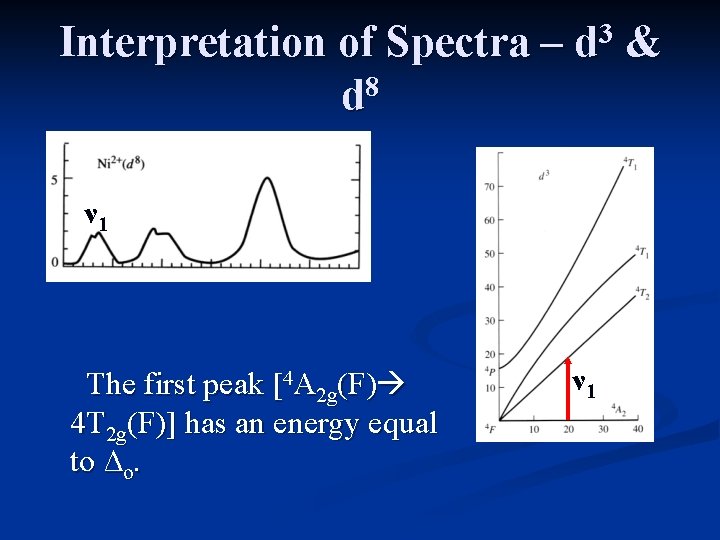
Interpretation of Spectra – 8 d 3 d ν 1 The first peak is due to the 4 A (F) 4 T (F) transition. 2 g 2 g &

Interpretation of Spectra – 8 d ν 1 3 d ν 2 The second peak is due to the 4 A 2 g(F) 4 T 1 g(F) transition. ν 2 &

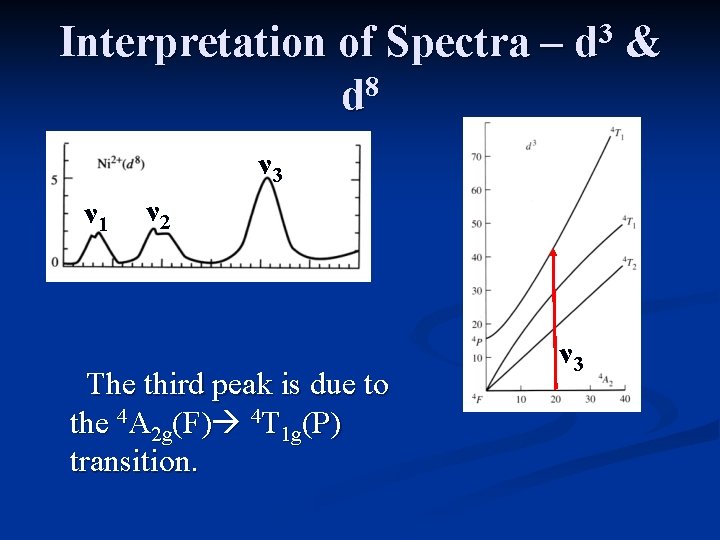
Interpretation of Spectra – 8 d 3 d ν 3 ν 1 ν 2 The third peak is due to the 4 A 2 g(F) 4 T 1 g(P) transition. ν 3 &

Interpretation of Spectra – 8 d 3 d ν 1 The first peak [4 A 2 g(F) 4 T 2 g(F)] has an energy equal to ∆o. ν 1 &

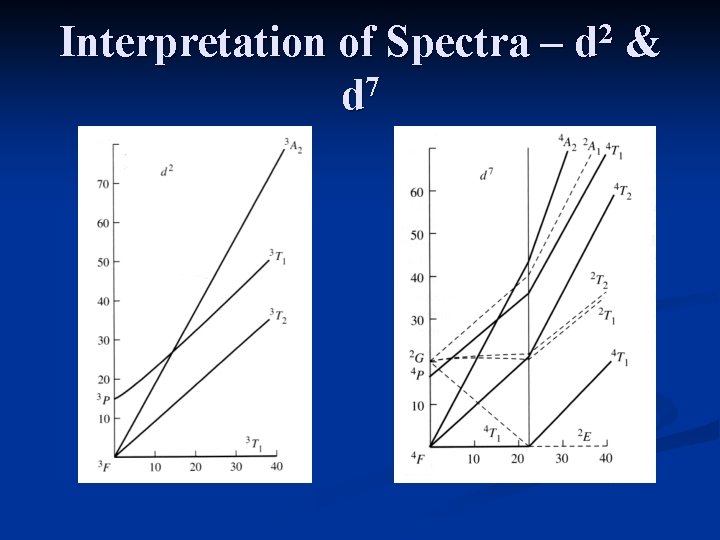
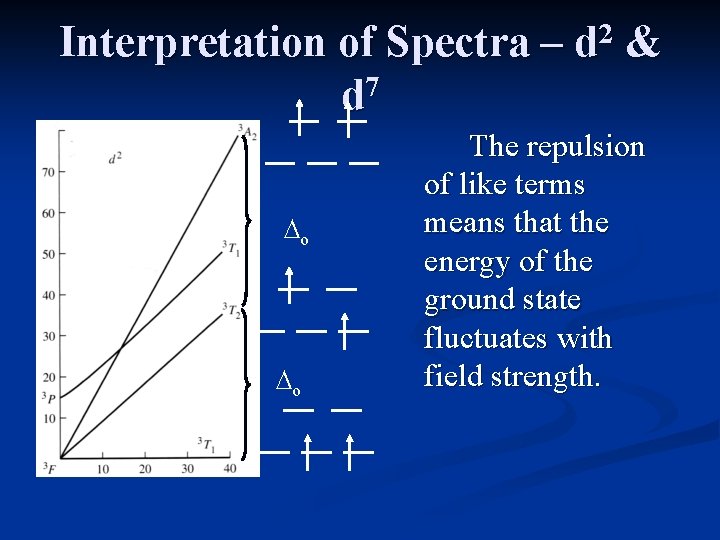
Interpretation of Spectra – 7 d 2 d & The interpretation of spectra from d 2 or d 7 (high spin) complexes is the most complicated due to curvature in the ground state of the Tanabe-Sugano diagrams. Since the ground state and an excited state have the same symmetry (4 T 1 g), they mix and curve away from each other.

Interpretation of Spectra – 7 d 2 d &

Interpretation of Spectra – 7 d ∆o ∆o 2 d & The repulsion of like terms means that the energy of the ground state fluctuates with field strength.

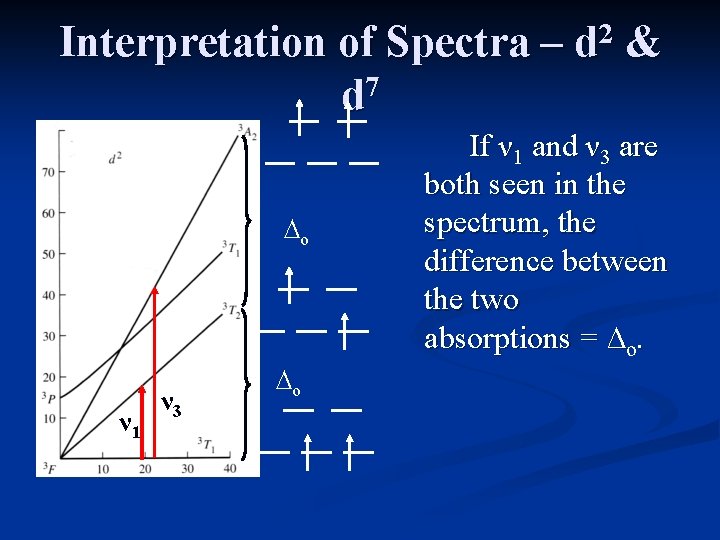
Interpretation of Spectra – 7 d ∆o ν 1 ν 3 ∆o 2 d & If ν 1 and ν 3 are both seen in the spectrum, the difference between the two absorptions = ∆o.

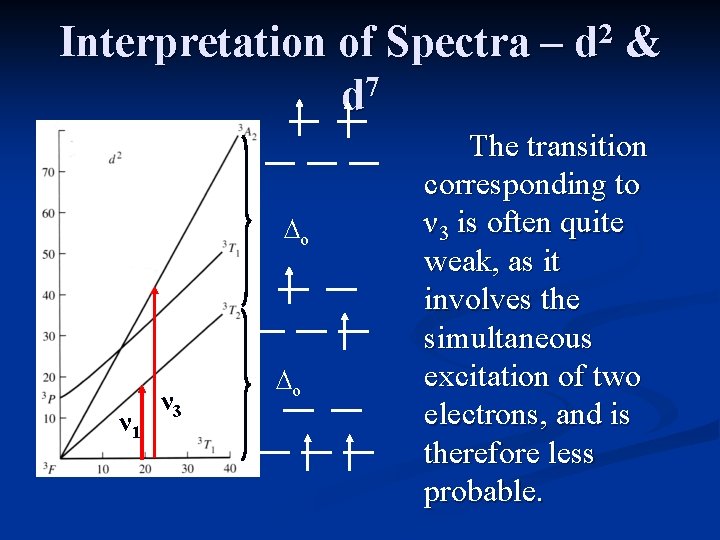
Interpretation of Spectra – 7 d ∆o ν 1 ν 3 ∆o 2 d & The transition corresponding to ν 3 is often quite weak, as it involves the simultaneous excitation of two electrons, and is therefore less probable.

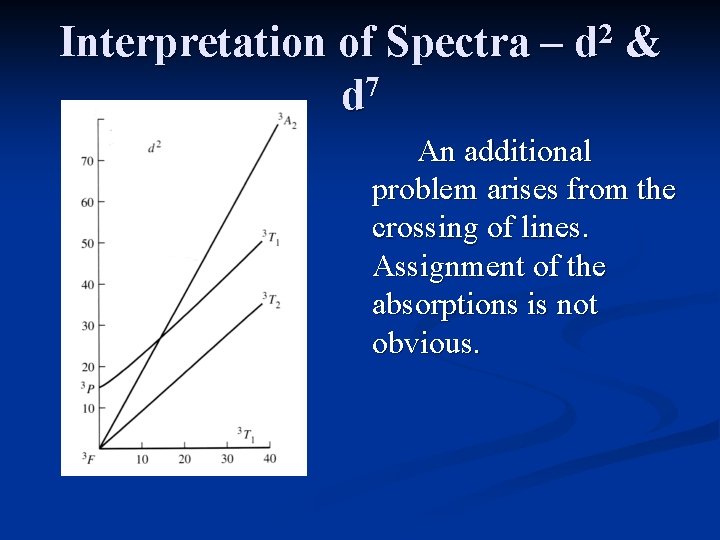
Interpretation of Spectra – 7 d 2 d & It is not easy to assign the absorptions due to several complications: 1. Lines cross in the Tanabe-Sugano diagram, making assignment difficult 2. The second and third absorptions may overlap, making it difficult to determine the actual position of the peaks

Interpretation of Spectra – 7 d 2 d & An additional problem arises from the crossing of lines. Assignment of the absorptions is not obvious.

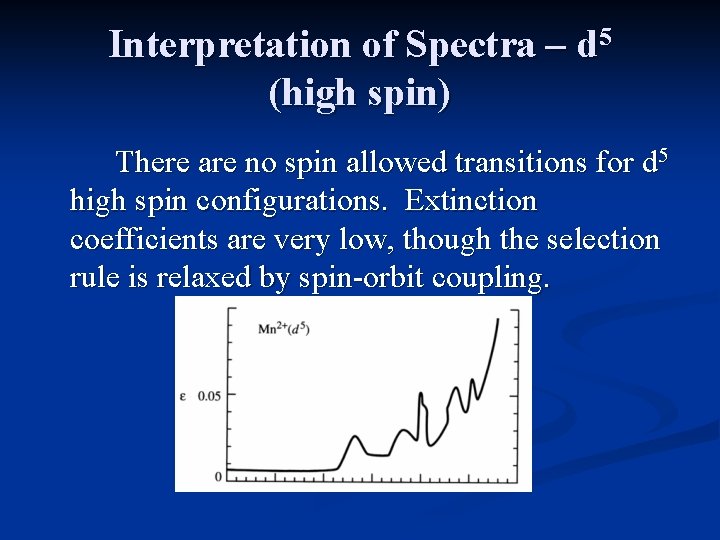
Interpretation of Spectra – d 5 (high spin) There are no spin allowed transitions for d 5 high spin configurations. Extinction coefficients are very low, though the selection rule is relaxed by spin-orbit coupling.

Interpretation of Spectra – d 5 (high spin) Mn 2+ compounds are white to pale pink in color.

Charge Transfer Spectra Many transition metal complexes exhibit strong charge-transfer absorptions in the UV or visible range. These are much more intense than d d transitions, with extinction coefficients ≥ 50, 000 L/mol-cm (as compared to 20 L/mol-cm for d d transitions).

Charge Transfer Spectra Examples of these intense absorptions can be seen in the permanganate ion, Mn. O 4 -. They result from electron transfer between the metal and the ligands.

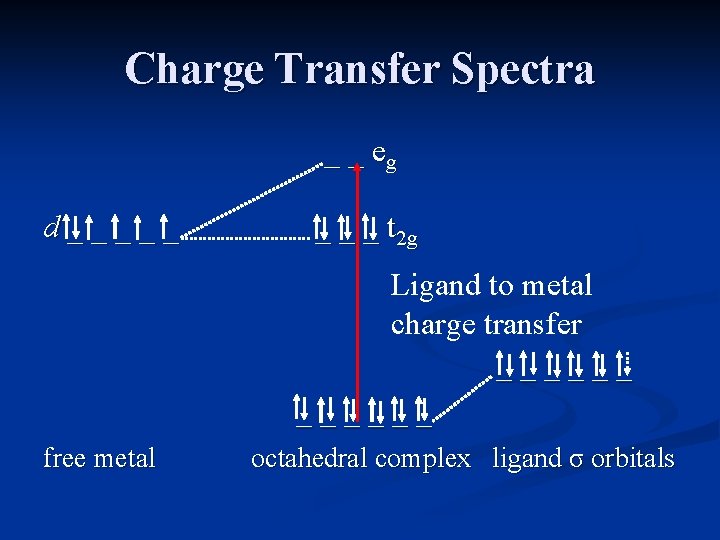
Charge Transfer Spectra In charge transfer absorptions, electrons from molecular orbitals that reside primarily on the ligands are promoted to molecular orbitals that lie primarily on the metal. This is known as a charge transfer to metal (CTTM) or ligand to metal charge transfer (LMCT). The metal is reduced as a result of the transfer.

Charge Transfer Spectra _ _ eg d _ _ _ t 2 g Ligand to metal charge transfer _ _ _ free metal octahedral complex ligand σ orbitals

Ligand to Metal Charge Transfer LMCT occurs in the permangate ion, Mn. O 41 -. Electrons from the filled p orbitals on the oxygens are promoted to empty orbitals on the manganese. The result is the intense purple color of the complex.

Ligand to Metal Charge Transfer LMCT typically occurs in complexes with the metal in a fairly high oxidation state. It is the cause of the intense color of complexes in which the metal, at least formally, has no d electrons (Cr. O 42 -, Mn. O 41 -).

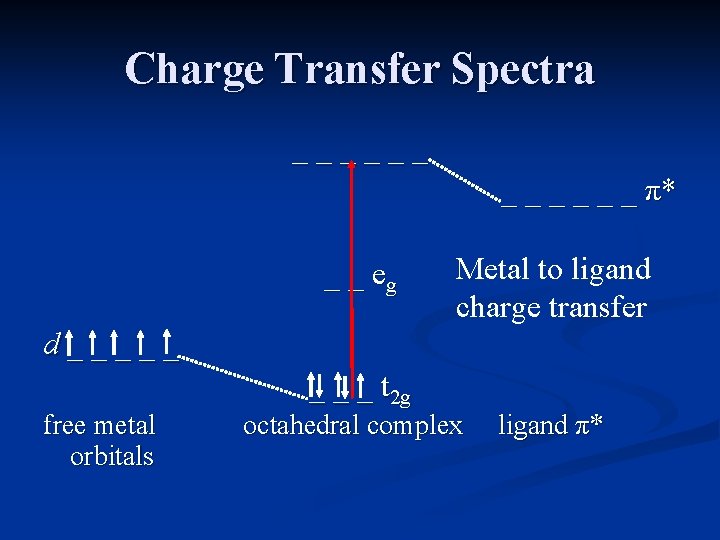
Metal to Ligand Charge Transfer MLCT typically occurs in complexes with π acceptor ligands. The empty π* orbitals on the ligands accept electrons from the metal upon absorption of light. The result is oxidation of the metal.

Charge Transfer Spectra _ _ _ π* _ _ eg d _ _ _ free metal orbitals _ _ _ t 2 g Metal to ligand charge transfer octahedral complex ligand π*

Metal to Ligand Charge Transfer Examples of LMCT include iron(III) with acceptor ligands such as CN- or SCN 1 -. The complex absorbs light and oxidizes the iron to a +4 oxidation state.

Metal to Ligand Charge Transfer The metal may be in a low oxidation state (0) with carbon monoxide as the ligand. Many of these complexes are brightly colored, and some appear to exhibit both types of electron transfer.