The Electronic Spectra of Coordination Compounds General Features

The Electronic Spectra of Coordination Compounds

General Features Absorption bands in electronic spectra are usually broad, and occur much more rapidly than molecular vibrations. As a result, the spectra represent a “snapshot” of molecules in various vibrational and rotational states.

General Features Extinction coefficients will range from <1 up to 50, 000 M-1 cm-1 depending upon the type of electronic transition and whether it is permitted based on selection rules.

Selection Rules Electronic transitions obey the following selection rules: 1. ∆S = 0. Electrons cannot change spin. 2. There must be a change in parity. Only g u or u g transitions are allowed. Thus, all d d transitions are forbidden by the Laporte selection rule.

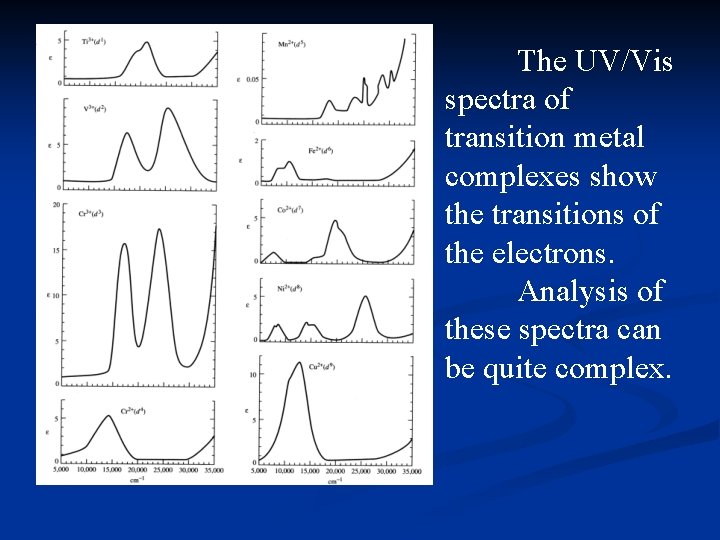
The UV/Vis spectra of transition metal complexes show the transitions of the electrons. Analysis of these spectra can be quite complex.

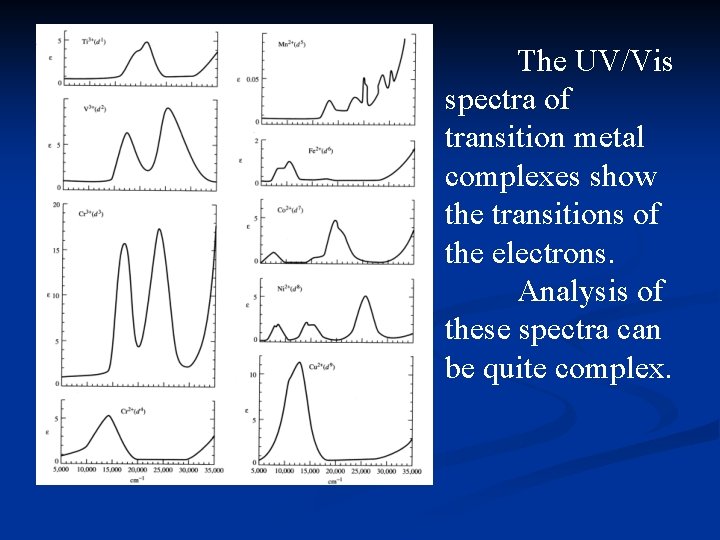
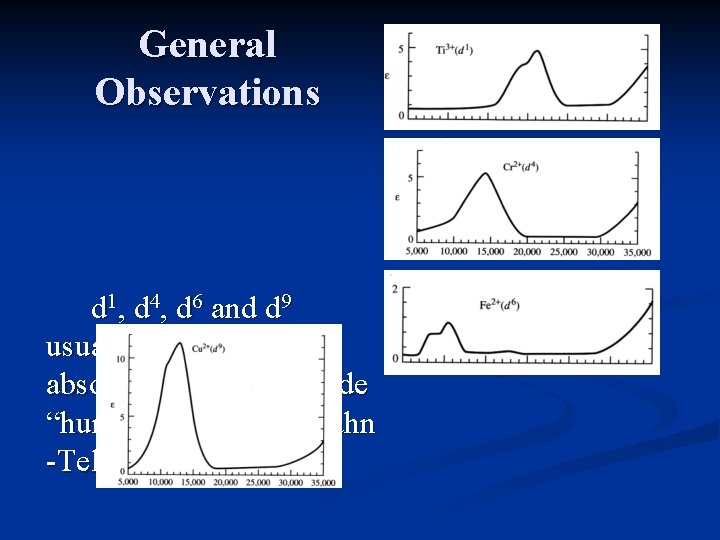
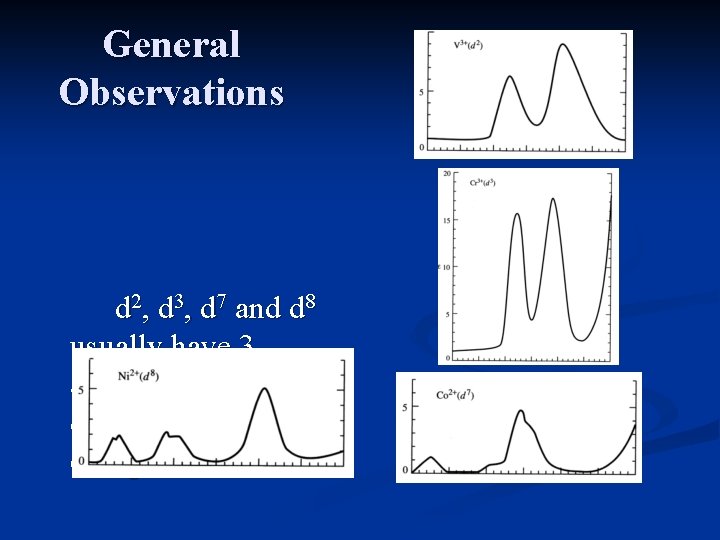
Summary of Observations-First Row Transition Metal Complexes (high spin) d 1, d 4, d 6 and d 9 complexes show one absorption. n d 2, d 3, d 7 and d 8 complexes show three absorptions, with the 3 rd peak often obscured. n d 5 complexes show very weak, sharp absorptions. n

The UV/Vis spectra of transition metal complexes show the transitions of the electrons. Analysis of these spectra can be quite complex.

Electron Spectra The UV/Vis spectra are used to determine the value of ∆o for the complex. The spectra arise from electronic transitions between the t 2 g and eg sets of molecular orbitals. Electronelectron interactions can greatly complicate the spectra. Only in the case of a single electron is interpretation of the spectrum straightforward.

Obtaining ∆o For a d 1 configuration, only a single peak is seen. It results from the electron promotion from the t 2 g orbitals to the eg orbitals. The “toothed” appearance of the peak is due to a Jahn-Teller distortion of the excited state. The energy of the peak = ∆o.

General Observations d 1, d 4, d 6 and d 9 usually have 1 absorption, though a side “hump” results from Jahn -Teller distortions.

General Observations d 2, d 3, d 7 and d 8 usually have 3 absorptions, one is often obscured by a charge transfer band.

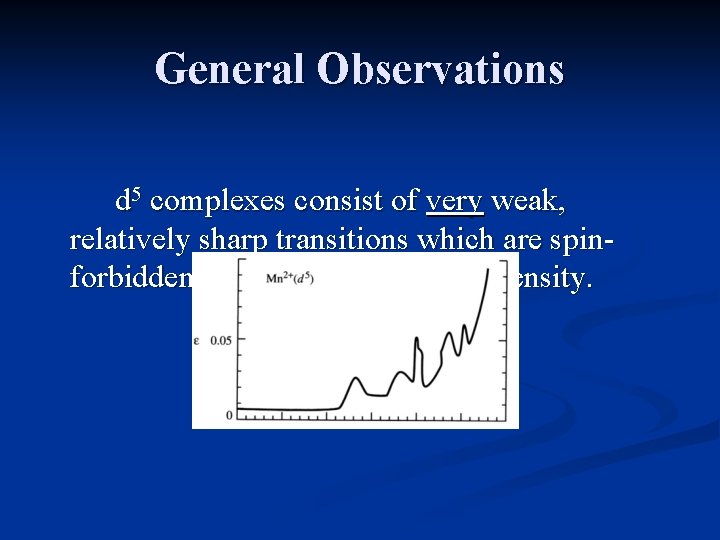
General Observations d 5 complexes consist of very weak, relatively sharp transitions which are spinforbidden, and have a very low intensity.

Qualitative Explanation Consider a V(III) complex such as [V(OH 2)6]3+. The ground state configuration is: ____ We might expect to see dz 2 dx 2 -y 2 only two peaks: One for the promotion of ____ one electron from the t 2 g dxy dyz dxz orbitals to the eg orbitals

Qualitative Explanation And a second peak for the promotion of both electrons to the eg set of orbitals. ____ dz 2 dx 2 -y 2 ____ dxy dyz dxz

d 2 Configuration A close examination of the environment of the electrons in each of the d orbitals shows that the promotion of a single electron can involve several different changes in energy.

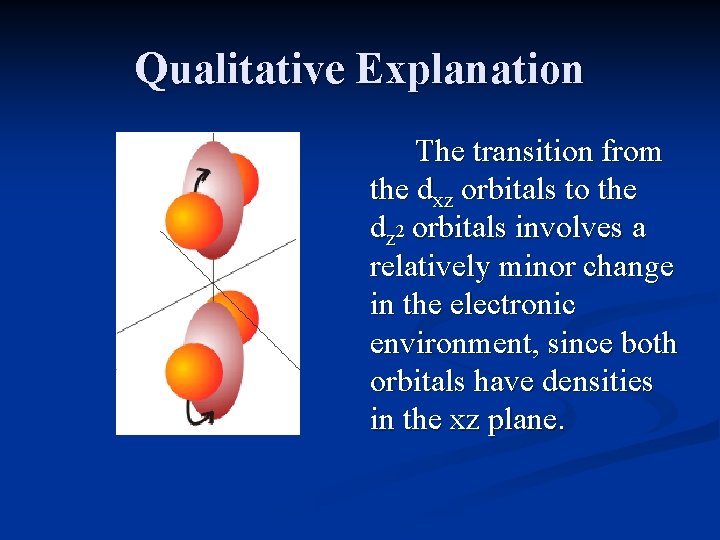
Qualitative Explanation The transition from the dxz orbitals to the dz 2 orbitals involves a relatively minor change in the electronic environment, since both orbitals have densities in the xz plane.

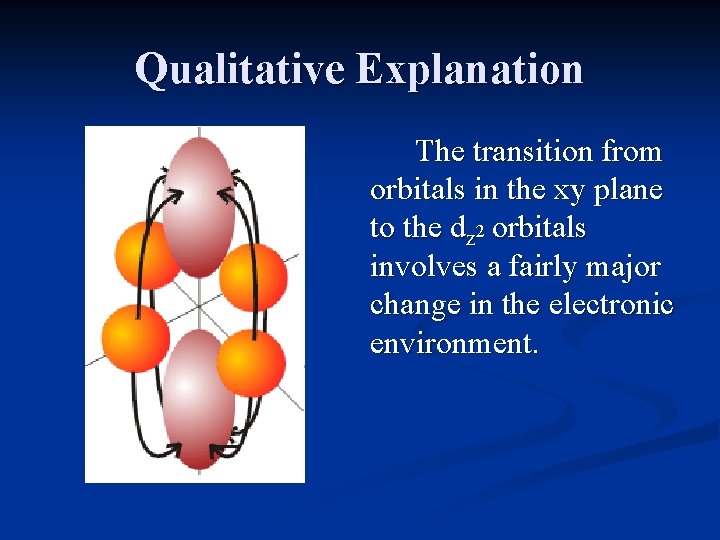
Qualitative Explanation A transition from the dxy to the dz 2, or the dyz or dxz to the dx 2 -y 2 orbitals involve a major ____ change in environment. dz 2 dx 2 -y 2 ____ dxy dyz dxz

Qualitative Explanation The transition from orbitals in the xy plane to the dz 2 orbitals involves a fairly major change in the electronic environment.

Qualitative Explanation Since the promotion of an electron from the t 2 g set of orbitals to the eg set can involve differing changes in environment, several peaks will be seen in the spectrum. Three peaks are predicted, and often observed. One of the peaks is sometimes obscured by an intense charge transfer band.

3 d Multi-electron Complexes For complexes with more than one electron in the 3 d (and 4 s) orbitals of the metal, electron interactions must be considered. The electrons are not independent of each other, and the orbital angular momenta (ml values) and the spin angular momenta (ms values) interact.

4 d and 5 d Metal Complexes The lower transition metals undergo further coupling (called j-j coupling or spin-orbit coupling).

3 d Multi-electron Complexes The interaction is called Russel-Saunders or L-S coupling. The interactions produce atomic states called microstates that are described by a new set of quantum numbers. ML = total orbital angular momentum =Σml MS = total spin angular momentum = Σms

Determining the Energy States of an Atom A microstate table that contains all possible combinations of ml and ms is constructed. Each microstate represents a possible electron configuration. Both ground state and excited states are considered.

Energy States Microstates would have the same energy only if repulsion between electrons is negligible. In an octahedral or tetrahedral complex, microstates that correspond to different relative spatial distributions of the electrons will have different energies. As a result, distinguishable energy levels, called terms are seen.

Energy States To obtain all of the terms for a given electron configuration, a microstate table is constructed. The table is a grid of all possible electronic arrangements. It lists all of the possible values of spin and orbital orientation. It includes both ground and excited states, and must obey the Pauli Exclusion Principle.

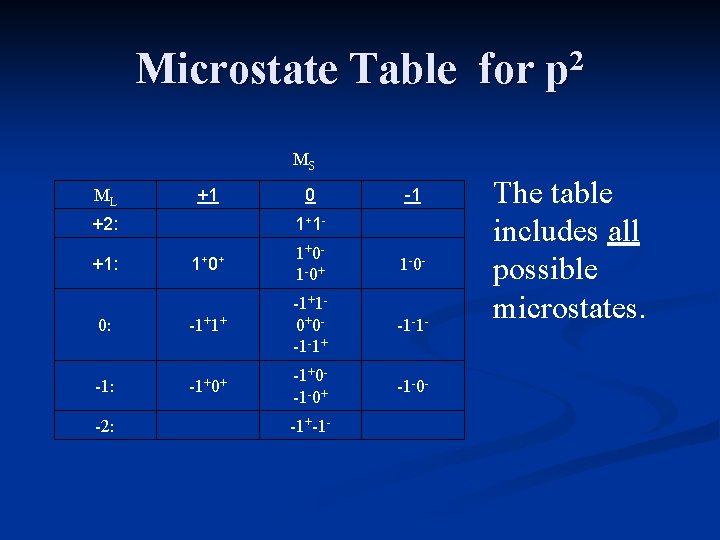
Constructing a Microstate Table Consider an atom of carbon. Its highest occupied orbital has a p 2 electron configuration. Microstates correspond to the various possible occupation of the px, py and pz orbitals.

Constructing a Microstate Table ml = +1 0 -1 Configurations: ___ ___ ___ microstate: (1+, 0+) (0+, -1+) (1+, -1+) These are examples of some of the ground state microstates. Others would have the electrons (arrows) pointing down.

Constructing a Microstate Table ml = +1 0 -1 Configurations: ___ ___ ___ microstate: (1+, 1 -) (0+, 0 -) (-1+, -1 -) These are examples of some of the excited state microstates.

Microstate Table for p 2 For the carbon atom, ML will range from +2 down to -2, and MS can have values of +1 (both electrons “pointing up”), 0 (one electron “up”, one electron “down), or -1 (both electrons “pointing down”).

Microstate Notation For the carbon atom, ML will range from +2 down to -2, and MS can have values of +1 (both electrons “pointing up”), 0 (one electron “up”, one electron “down), or -1 (both electrons “pointing down”).

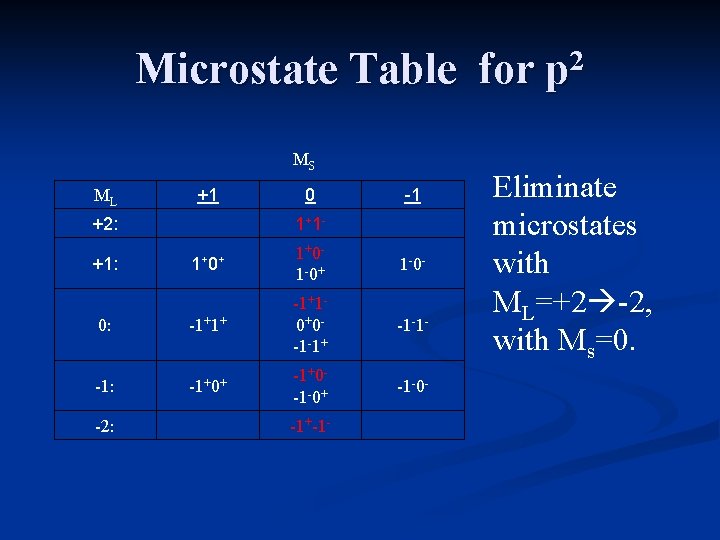
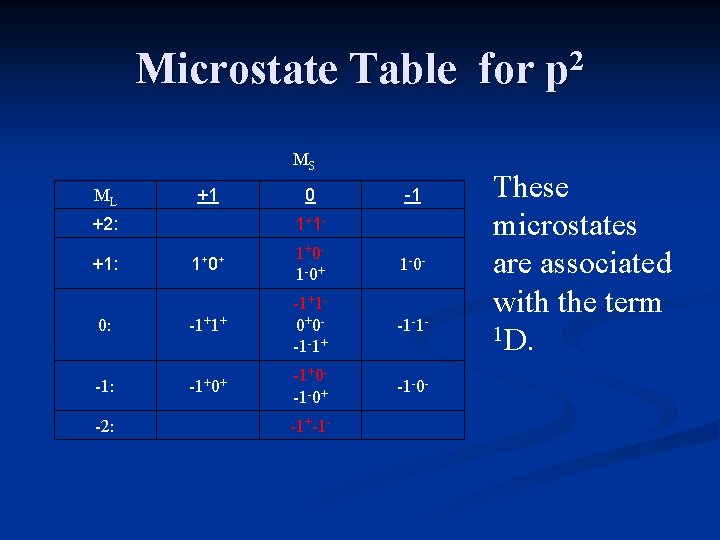
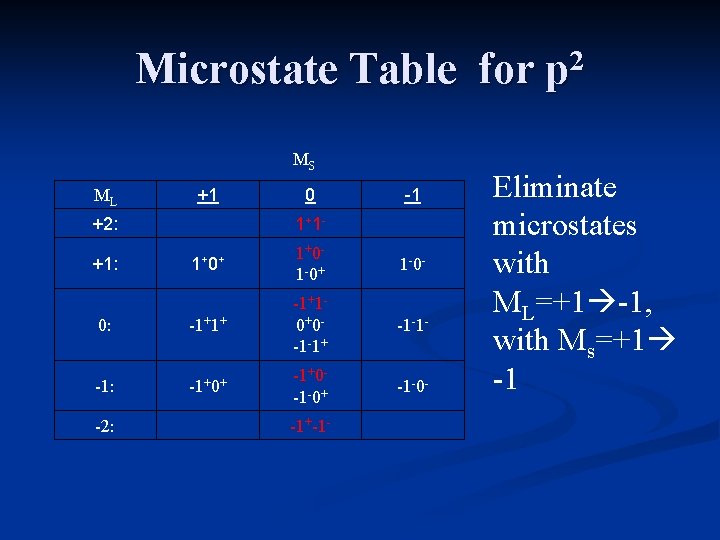
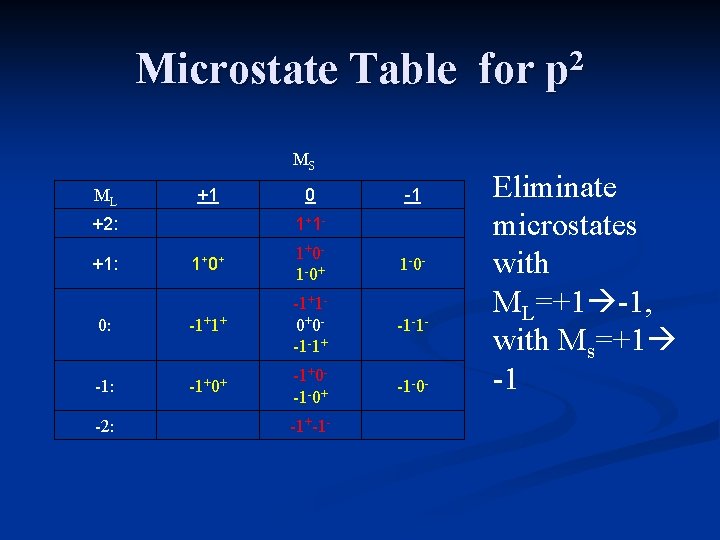
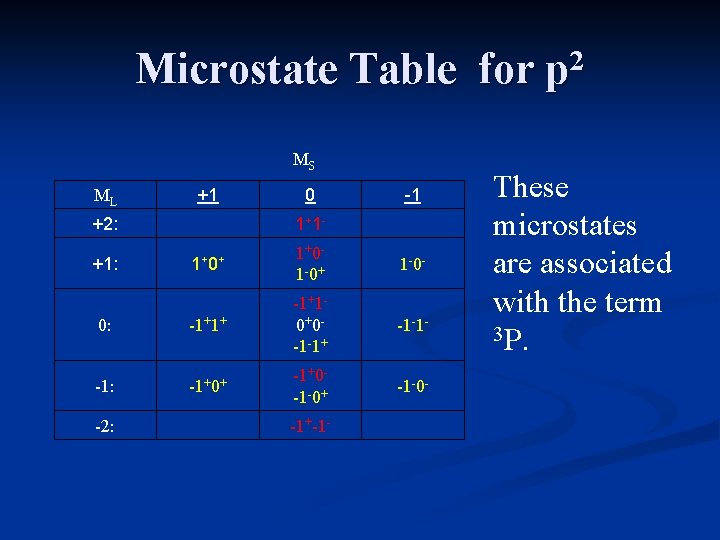
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - The table includes all possible microstates.

Constructing a Microstate Table Once the microstate table is complete, the microstates are collected or grouped into atomic (coupled) energy states.

Constructing a Microstate Table For two electrons, L = l 1+ l 2, l 1+ l 2 -1, l 1+ l 2 -2, …│l 1 - l 2│ For a p 2 configuration, L = 1+1, 1+1 -1, 1 -1. The values of L are: 2, 1 and 0. L is always positive, and ranges from the maximum value of Σl.

Constructing a Microstate Table For two electrons, S = s 1+ s 2, s 1+ s 2 -1, s 1+ s 2 -2, …│s 1 - s 2│ For a p 2 configuration, S = ½ + ½ , ½ + ½ -1. The values of S are: 1 and 0.

Atomic Quantum Numbers Quantum numbers L and S describe collections of microstates, whereas ML and MS describe the individual microstates themselves.

Constructing a Microstate Table The microstate table is a grid that includes all possible combinations of L, the total angular momentum quantum number, and S, the total spin angular momentum quantum number. For two electrons, L = l 1+ l 2, l 1+ l 2 -1, l 1+ l 2 -2, …│l 1 - l 2│ S = s 1+ s 2, s 1+ s 2 -1, s 1+ s 2 -2, …│s 1 - s 2│

Constructing a Microstate Table Once the microstate table is complete, all microstates associated with an energy state with specific value of L and S are grouped. It doesn’t matter which specific microstates are placed in the group. Microstates are grouped and eliminated until all microstates are associated with a specific energy state or term.

Term Symbols Each energy state or term is represented by a term symbol. The term symbol is a capitol letter that is related to the value of L. L = 0 1 2 3 4 Term Symbol S P D F G

Term Symbols The upper left corner of the term symbol contains a number called the multiplicity. The multiplicity is the number of unpaired electrons +1, or 2 S+1.

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+2 -2, with Ms=0.

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - These microstates are associated with the term 1 D.

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+1 -1, with Ms=+1 -1

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - Eliminate microstates with ML=+1 -1, with Ms=+1 -1

Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - These microstates are associated with the term 3 P.

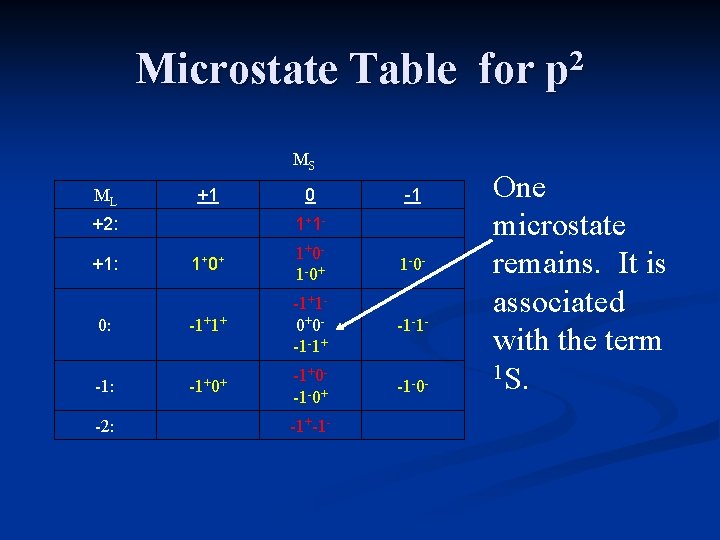
Microstate Table for p 2 MS ML +1 +2: 0 1+ 1 - -1 1+ 0+ 1+0 - 1 -0+ 1 -0 - 0: -1+1+ -1+1 - 0+0 - -1 -1+ -1 -1 - -1: -1+0+ -1+0 - -1 -0+ -1 -0 - +1: -2: -1+-1 - One microstate remains. It is associated with the term 1 S.

Term States for p 2 The term states for a p 2 electron configuration are 1 S, 3 P, and 1 D. The term symbol with the greatest multiplicity and highest value of ML will be the ground state. 3 P is the ground state term for carbon.

Determining the Relative Energy of Term States 1. For a given electron configuration, the term with the greatest multiplicity lies lowest in energy. (This is consistent with Hund’s rule. ) 2. For a term of a given multiplicity, the greater the value of L, the lower the energy.

Determining the Relative Energy of Term States For a p 2 configuration, the term states are 3 P, 1 D and 1 S. The terms for the free atom should have the following relative energies: 3 P< 1 D <1 S

Determining the Relative Energy of Term States The rules for predicting the ground state always work, but they may fail in predicting the order of energies for excited states.

Energy States for a d 2 Configuration A microstate table for a d 2 electron configuration will contain 45 microstates (ML = 4 -4, and MS=1, 0 or -1) associated with the following terms: 1 S, 1 D, 1 G, 3 P, and 3 F

Energy States for a d 2 Configuration n Problem: Determine the ground state of a free atom with a d 2 electron configuration, and place the terms in order of increasing energy. 1 S, 1 D, 1 G, 3 P, and 3 F

Determining the Ground State Term We only need to know the ground state term to interpret the spectra of transition metal complexes. This can be obtained without constructing a microstate table. The ground state will a) have the maximum multiplicity b) have the maximum value of ML for the configuration obtained in part (a).