The Electric Field Chapter 23 The Electric Field

The Electric Field Chapter 23

The Electric Field A group of fixed charges exerts a force F, given by Coulomb’s law, on a “test charge” q at position r. q r F • The electric field E (at a given point in space) is the force per unit charge that would be experienced by a test charge at that point. E=F/q This is a vector function of position; i. e. , a vector field.

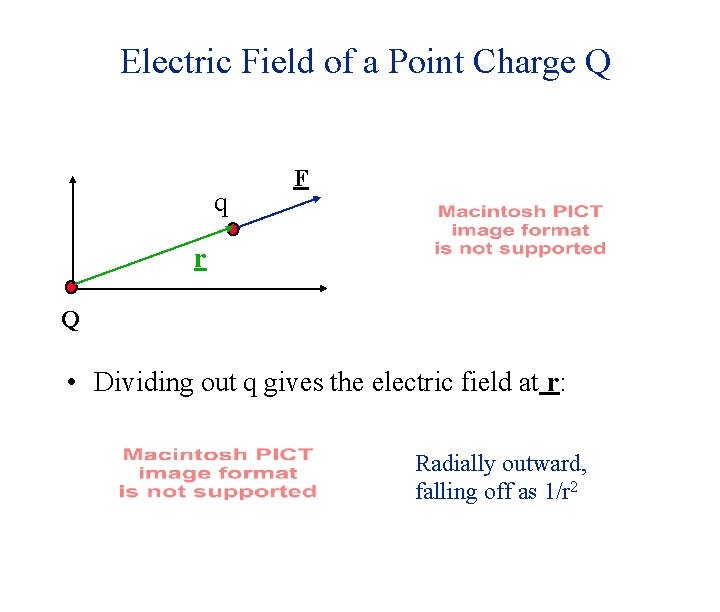
Electric Field of a Point Charge Q q F r Q • Dividing out q gives the electric field at r: Radially outward, falling off as 1/r 2

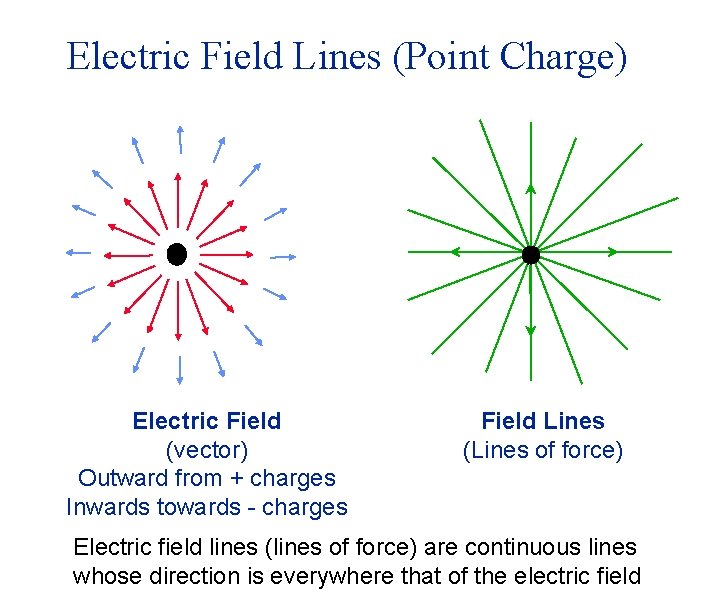
Electric Field Lines (Point Charge) Electric Field (vector) Outward from + charges Inwards towards - charges Field Lines (Lines of force) Electric field lines (lines of force) are continuous lines whose direction is everywhere that of the electric field

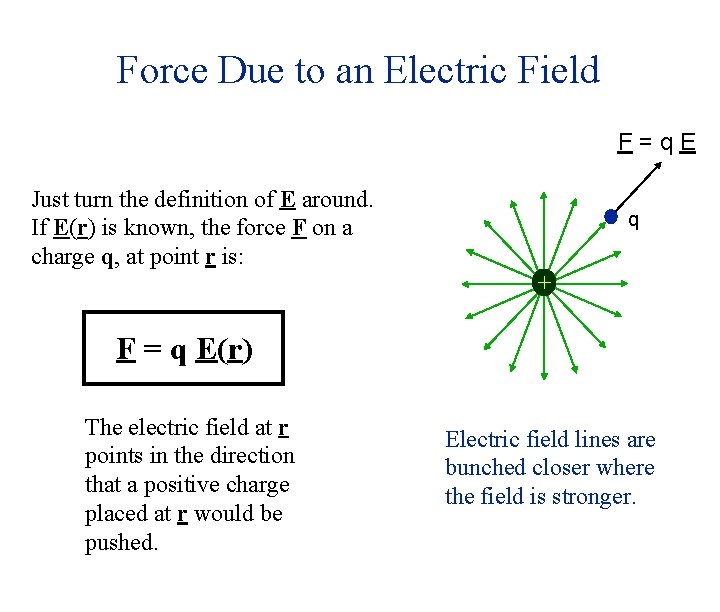
Force Due to an Electric Field F=q. E Just turn the definition of E around. If E(r) is known, the force F on a charge q, at point r is: q + F = q E(r) The electric field at r points in the direction that a positive charge placed at r would be pushed. Electric field lines are bunched closer where the field is stronger.

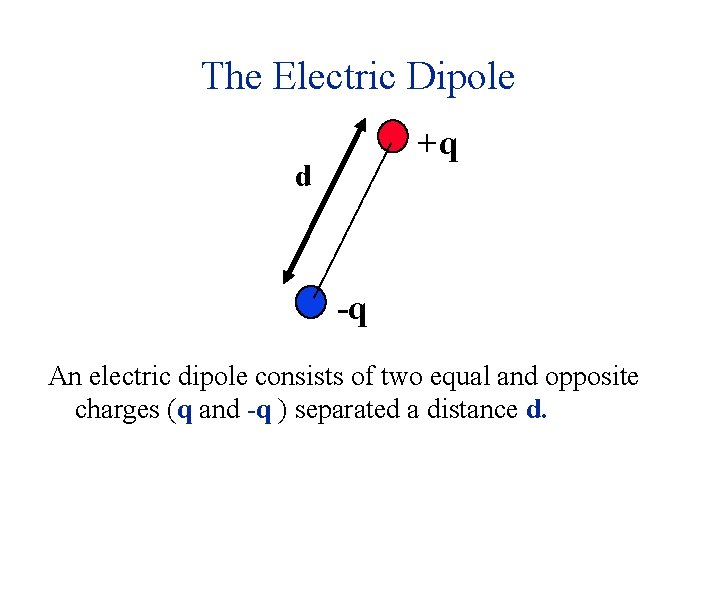
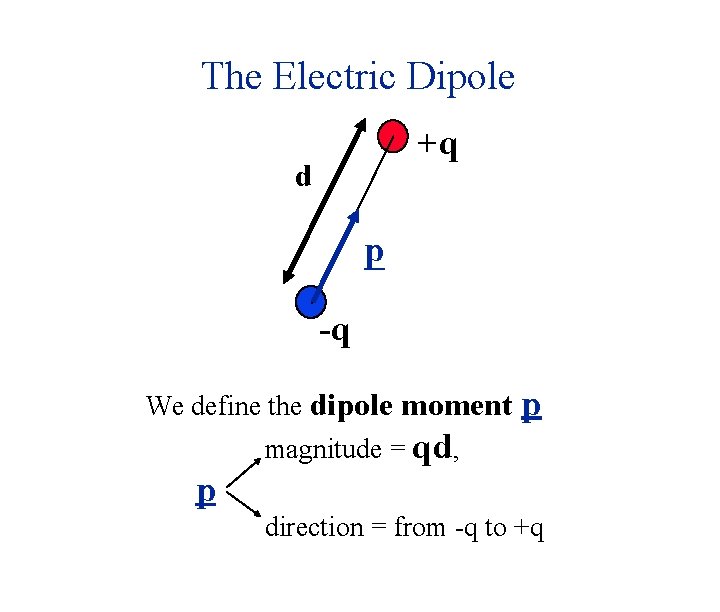
The Electric Dipole +q d -q An electric dipole consists of two equal and opposite charges (q and -q ) separated a distance d.

The Electric Dipole +q d p -q We define the dipole moment p magnitude = qd, p direction = from -q to +q

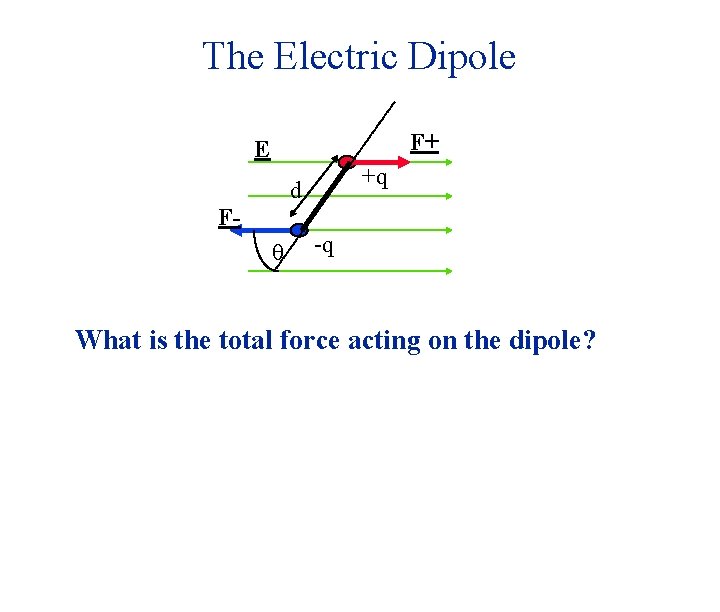
The Electric Dipole E +q d q -q Suppose the dipole is placed in a uniform electric field (i. e. , E is the same everywhere in space). Will the dipole move ? ?

The Electric Dipole E +q d q -q What is the total force acting on the dipole?

The Electric Dipole F+ E +q d Fq -q What is the total force acting on the dipole?

The Electric Dipole F+ E +q d Fq -q What is the total force acting on the dipole? Zero, because the force on the two charges cancel: both have magnitude q. E, and are opposite. The center of mass does not accelerate.

The Electric Dipole F+ E +q d Fq -q What is the total force acting on the dipole? Zero, because the force on the two charges cancel: both have magnitude q. E, and are opposite. The center of mass does not accelerate. But the charges start to move. Why?

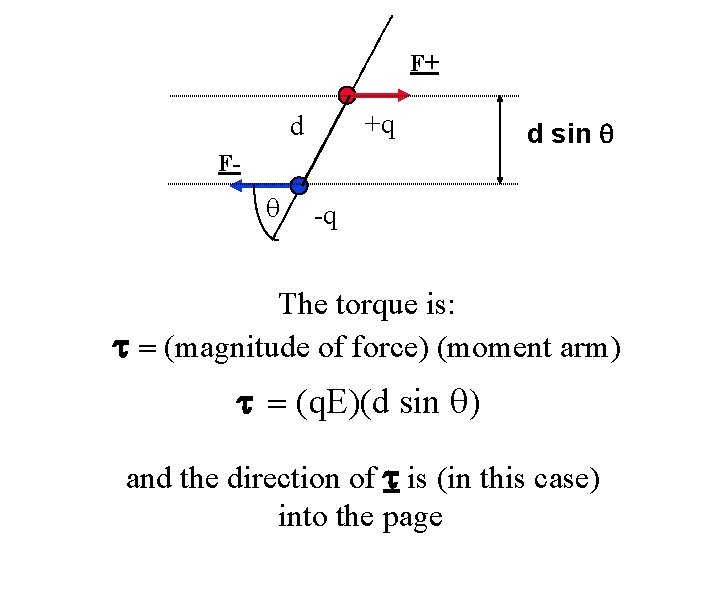
The Electric Dipole F+ E +q d Fq -q What is the total force acting on the dipole? Zero, because the force on the two charges cancel: both have magnitude q. E, and are opposite. The center of mass does not accelerate. But the charges start to move. Why? There’s a torque because the forces aren’t collinear.

F+ +q d d sin q F- q -q The torque is: t = (magnitude of force) (moment arm) t = (q. E)(d sin q) and the direction of t is (in this case) into the page

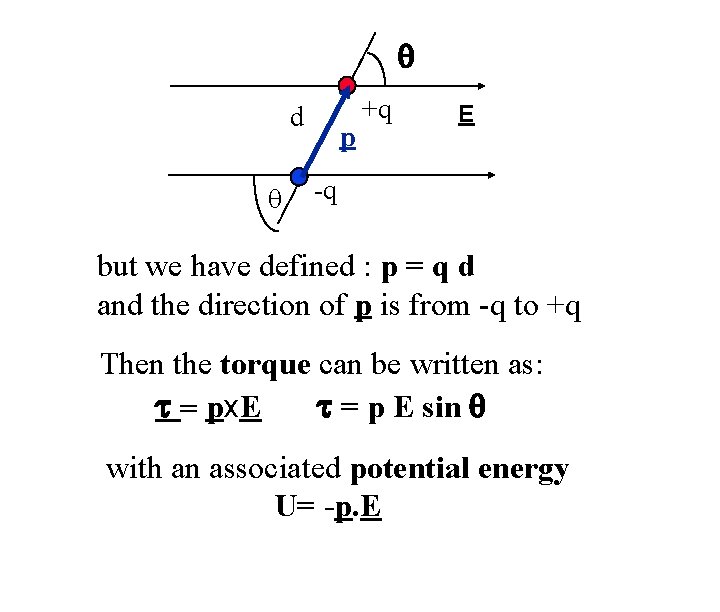
q d q p +q E -q but we have defined : p = q d and the direction of p is from -q to +q Then the torque can be written as: t = px. E t = p E sin q with an associated potential energy U= -p. E

Electric fields due to various charge distributions The electric field is a vector which obeys the superposition principle. Begin with a simple example with discrete charges: the dipole

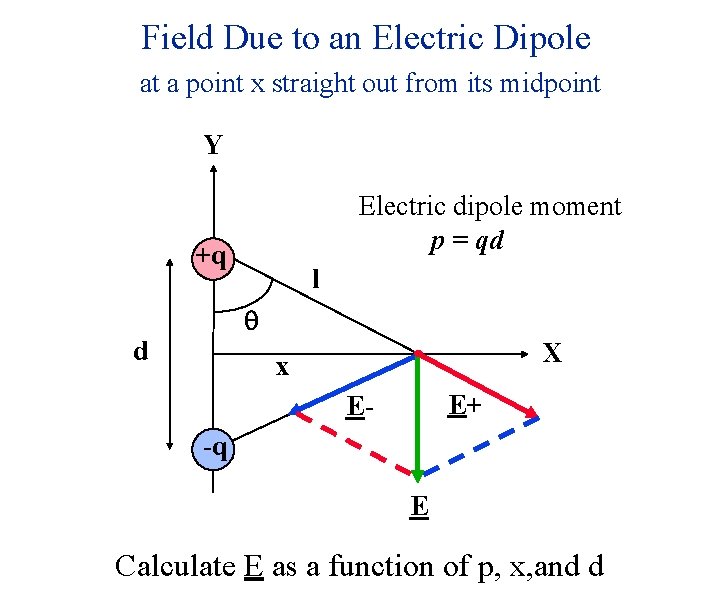
Field Due to an Electric Dipole at a point x straight out from its midpoint Y Electric dipole moment p = qd +q l q d X x E+ E-q E Calculate E as a function of p, x, and d

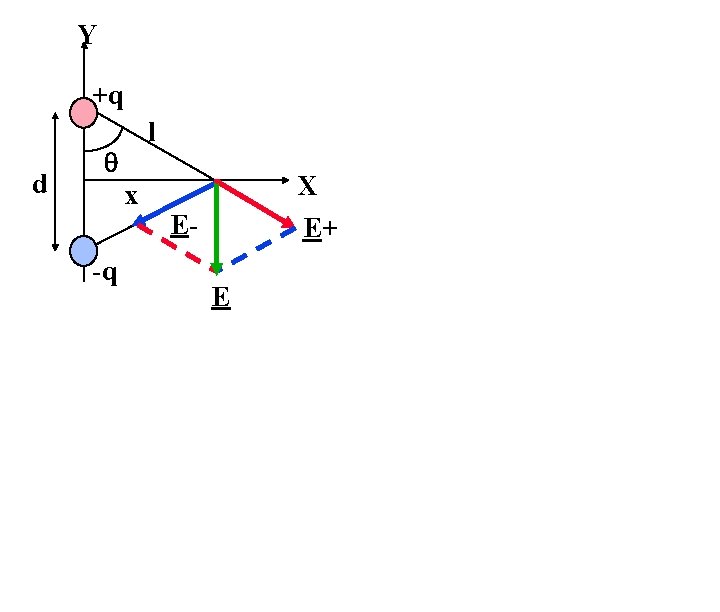
Y +q d l q x -q X E- E+ E

Electric Fields From Continuous Distributions of Charge Up to now we have only considered the electric field of point charges. Now let’s look at continuous distributions of charge lines - surfaces - volumes of charge and determine the resulting electric fields. Sphere Ring Sheet

Electric Fields From Continuous Distributions For discrete point charges, we can use the superposition principle and sum the fields due to each point charge: q 2 q 1 q 3 q 4

Electric Fields From Continuous Distributions For discrete point charges, we can use the superposition principle and sum the fields due to each point charge: q 2 q 1 q 3 q 4 What if we now have a continuous charge distribution? q E(r)

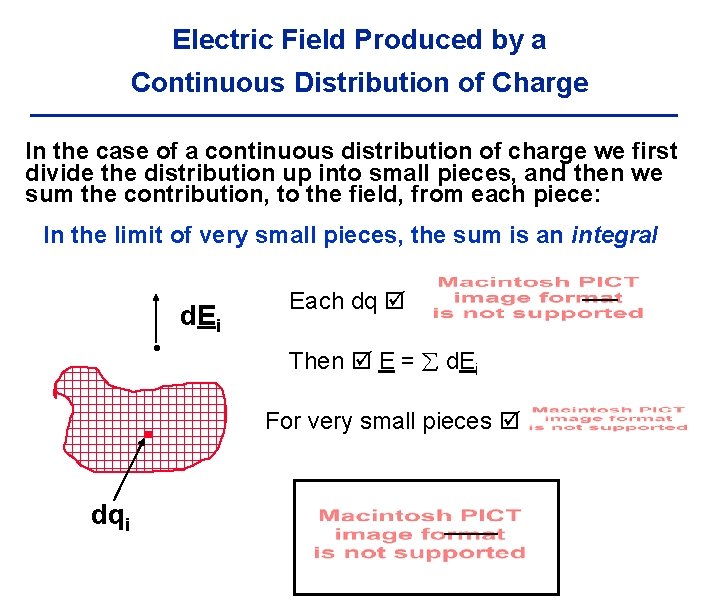
Electric Field Produced by a Continuous Distribution of Charge In the case of a continuous distribution of charge we first divide the distribution up into small pieces, and then we sum the contribution, to the field, from each piece: r d. Ei The small piece of charge dqi produces a small field d. Ei at the point r Note: dqi and d. Ei are differentials dqi In the limit of very small pieces, the sum is an integral

Electric Field Produced by a Continuous Distribution of Charge In the case of a continuous distribution of charge we first divide the distribution up into small pieces, and then we sum the contribution, to the field, from each piece: In the limit of very small pieces, the sum is an integral d. Ei dqi Each dq Then E = d. Ei For very small pieces

Continuous Charge Distributions charge density units differential LINE AREA VOLUME = Q / L = Q / A = Q / V C / m 2 C / m 3 dq = d. L dq = d. A dq = d. V Charge differential dq to be used when finding the electric field of a continuous charge distribution

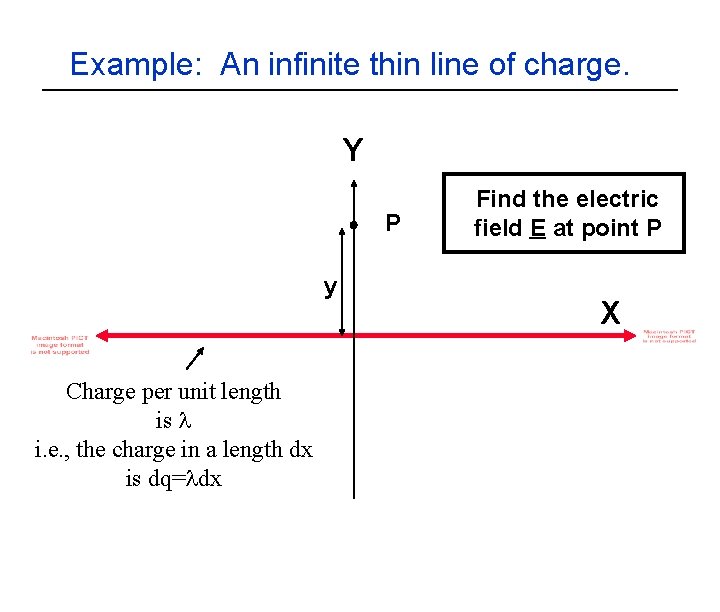
Example: An infinite thin line of charge. Y P y Charge per unit length is i. e. , the charge in a length dx is dq= dx Find the electric field E at point P X

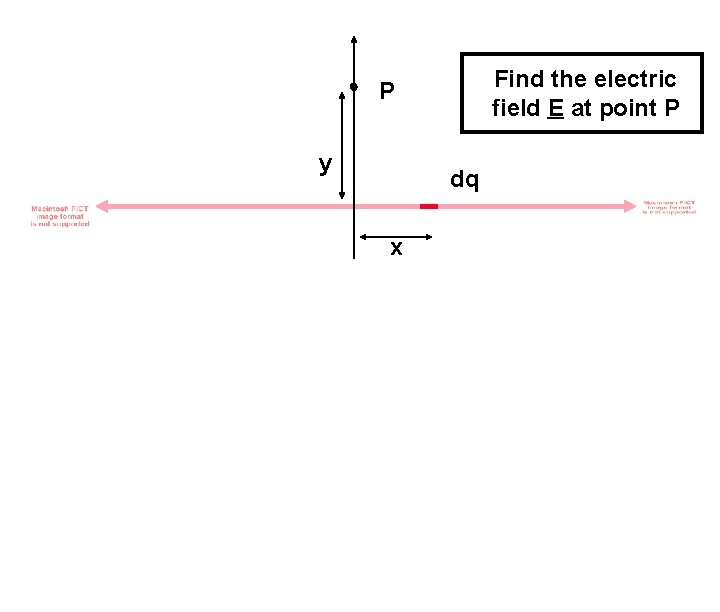
Find the electric field E at point P P y dq x

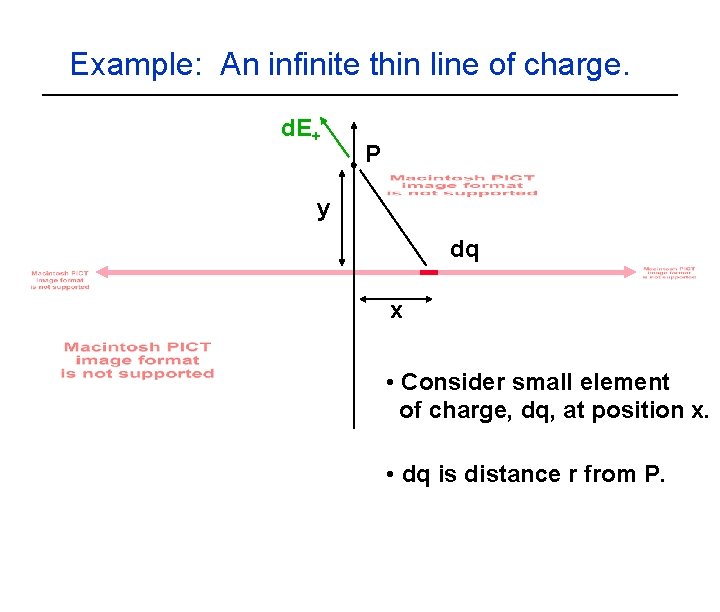
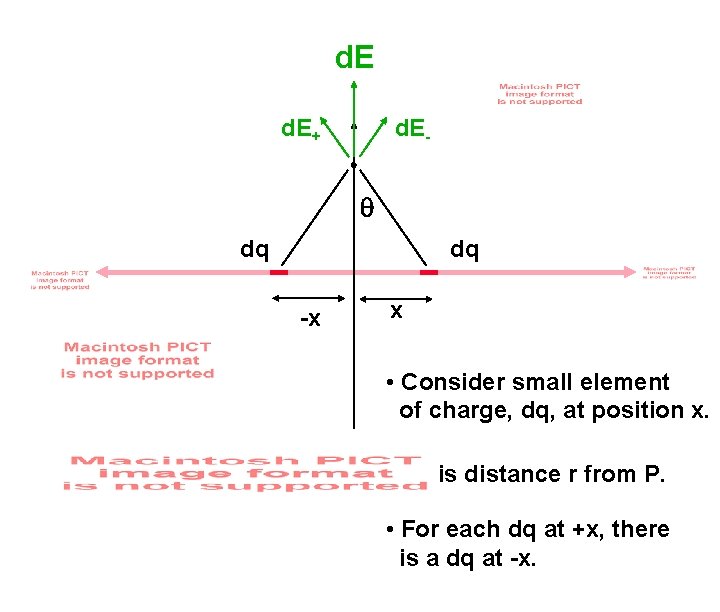
Example: An infinite thin line of charge. d. E+ P y dq x • Consider small element of charge, dq, at position x. • dq is distance r from P.

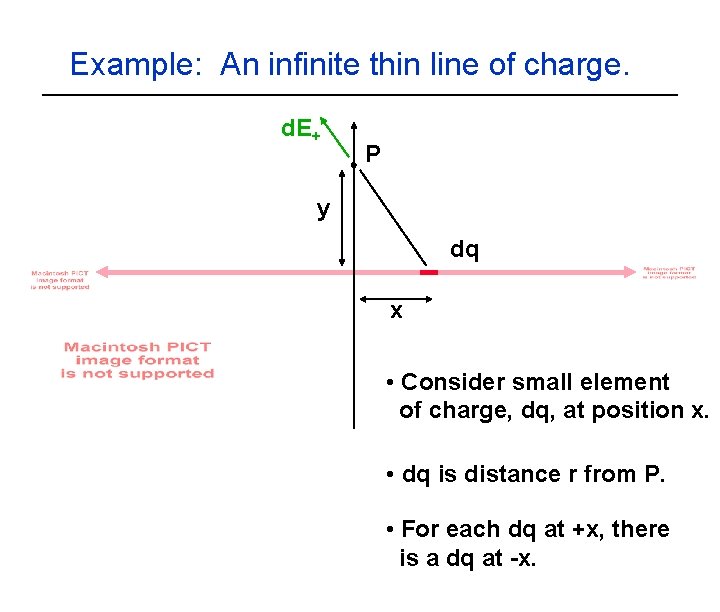
Example: An infinite thin line of charge. d. E+ P y dq x • Consider small element of charge, dq, at position x. • dq is distance r from P. • For each dq at +x, there is a dq at -x.

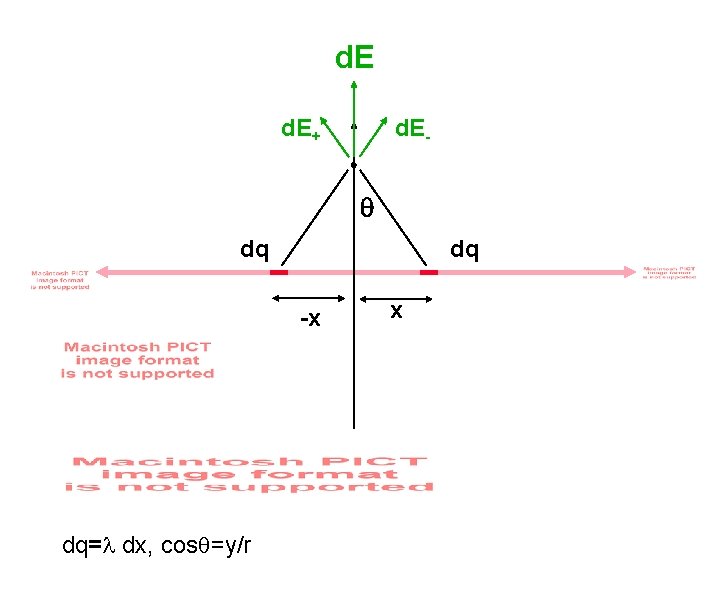
d. E+ d. E- q dq dq -x x • Consider small element of charge, dq, at position x. • dq is distance r from P. • For each dq at +x, there is a dq at -x.

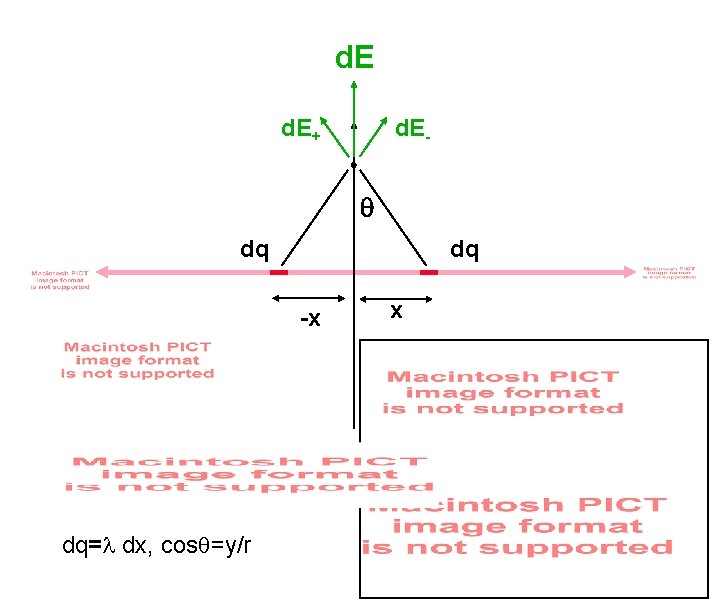
d. E+ d. E- q dq dq -x dq= dx, cosq=y/r x

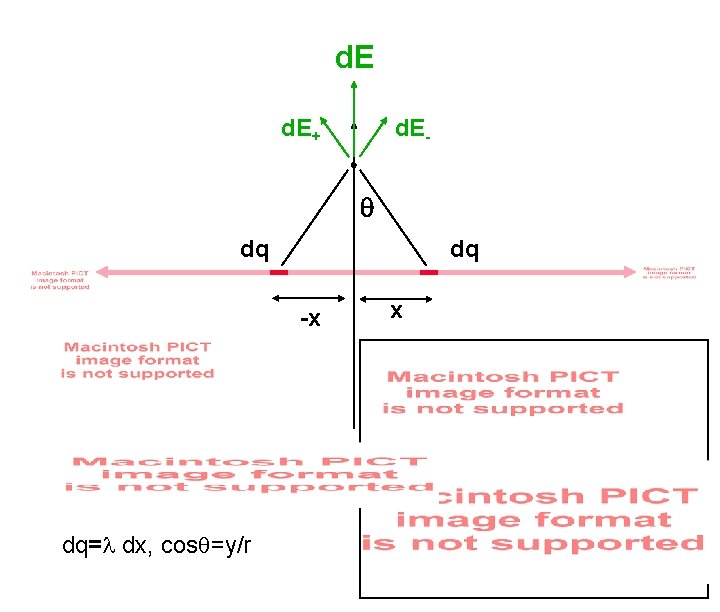
d. E+ d. E- q dq dq -x dq= dx, cosq=y/r x

d. E+ d. E- q dq dq -x dq= dx, cosq=y/r x

Example of Continuous Distribution: Ring of Charge Find the electric field at a point along the axis. Hint: be sure to use the symmetry of the problem! d. E z r dq Thin ring with total charge q charge per unit length is l=q/2 p. R R Break the charge up into little bits, and find the field due to each bit at the observation point. Then integrate.