The Efficiency of Algorithms Chapter 7 Chapter Contents

The Efficiency of Algorithms Chapter 7

Chapter Contents Motivation Measuring an Algorithm's Efficiency • Big Oh Notation Formalities Picturing Efficiency The Efficiency of Implementations of the ADT List • The Array-Based Implementation • The Linked Implementation • Comparing Implementations 2

Motivation Even a simple Multiplication program can be noticeably inefficient: 7562 x 423. Multiplication is equivalent to repeated addition. long first. Operand = 7562; long second. Operand = 423; long product = 0; for (; second. Operand > 0; second. Operand--) product = product + first. Operand; System. out. println(product); 3

Motivation When the 423 is changed to 100, 000 there is a significant delay in seeing the result When the 423 is changed to 1000, a even longer delay is noticed. • You may want to add one billion to zero 7562 times • May not always be faster, since one operand is not always much smaller than the other. 4

Motivation 756*423 = 7562 * ( 400 + 20 + 3) =7562 * 400 + 7562 * 20 + 7562 * 3 = 756, 200 * 4 + 75, 620 * 2 + 7, 562 * 3 Each of the term is the sum of d integers, where d is a digit in the second operand. This code executes faster than the previous code. Even simple program can be very inefficient depending on the implementation. Convinced that program’s efficiency does matter. 5

Measuring Algorithm Efficiency Algorithm has both time and space requirements called complexity to measure Types of complexity • Space complexity • Time complexity Analysis of algorithms • The measuring of either time/space complexity of an algorithm Measure the time complexity since it is more important Cannot compute actual time for an algorithm. Give function of problem size that is directly proportional to time requirement: growth-rate function Function measures how the time requirement grows as the problem size grows. • We usually measure worst-case time 6

Measuring Algorithm Efficiency Three algorithms for computing 1 + 2 + … n for an integer n > 0 7

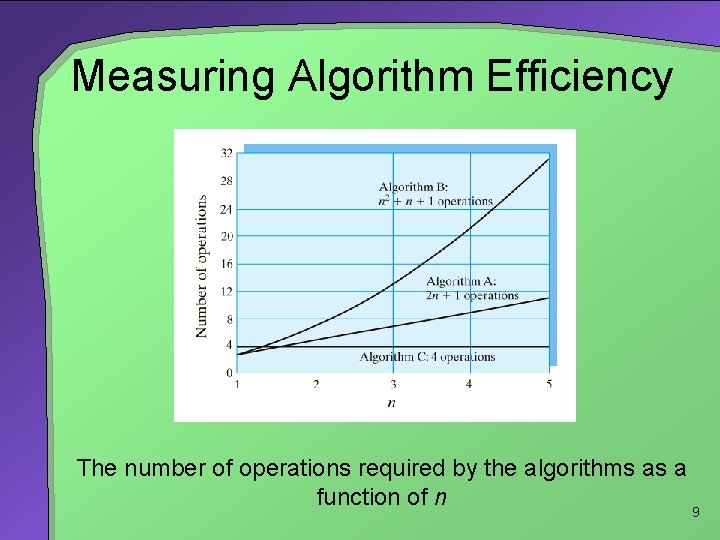
Measuring Algorithm Efficiency The number of operations required by the algorithms 8

Measuring Algorithm Efficiency The number of operations required by the algorithms as a function of n 9

Big Oh Notation Computer scientists use a notation to represent an algorithm’s complexity. To say "Algorithm A has a worst-case time requirement proportional to n" • We say A is O(n) • Read "Big Oh of n" or “order of at most n” For the other two algorithms • Algorithm B is O(n 2) • Algorithm C is O(1) 10

Big Oh Notation Grows in magnitude from left to right… Tabulates magnitudes of typical growth-rate functions evaluated at increasing values of n When analyzing the time efficiency of an algorithm, consider larger problems. For small problems, the difference between the execution time is usually insignificant. 11

Big Oh Notation The number of digits in an integer n compared with the integer portion of log 10 n O(loga n) = O(logb n) 12

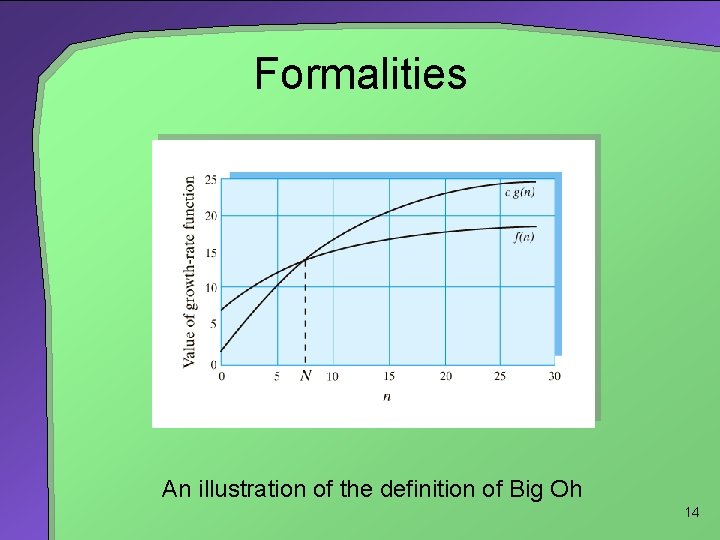
Formalities Formal mathematical definition of Big Oh An algorithm's time requirement f(n) is of order at most g(n) Big Oh provides an upper bound on a function’s growth rate. f(n) = O(g(n)) • That is, if a positive real number c and positive integer N exist such that f(n) ≤ c • g(n) for all n ≥ N c • g(n) is the upper bound on f(n) when n is sufficiently large. 13

Formalities An illustration of the definition of Big Oh 14

Example Show that f(n) = 5*n + 3 = O(n) g(n) = n, c = 6, and N = 3 f(n) <= 6 g(n) Why don’t we let g(n) = n^2 ? Let g(n) = n^2, c=8, N =1 Although the conclusion is correct, it is not as tight as possible. You want the upper bound to be as small as possible, and you want it to involve simple functions. 15

Formalities The following identities hold for Big Oh notation: • O(k * f(n)) = O(f(n)) • O(f(n)) + O(g(n)) = O(f(n) + g(n)) • O(f(n)) * O(g(n)) = O(f(n) *g(n)) • By using these identities and ignoring smaller terms in a growth rate function, you can determine the order of complexity with little efforts. • O(4*n^2 + 50*n -10) = O(4*n^2) = O(n^2) 16

Picturing Efficiency Body of loop requires a constant amount of time O(1) an O(n) algorithm. 17

Picturing Efficiency An O(n 2) algorithm. 18

Picturing Efficiency Another O(n 2) algorithm. 19

Question? for i = 1 to n { for j = 1 to 5 sum = sum +1; } Using Gig Oh notation, what is the order of the computation time? 20

Get a Feel for Growth-rate Functions The effect of doubling the problem size on an algorithm's time requirement. 21

Get a Feel for Growth-rate Functions The time to process one million of problem size by algorithms of various orders at the rate of one million operations per second. 22

Comments on Efficiency A programmer can use O(n 2), O(n 3) or O(2 n) as long as the problem size is small At one million operations per second it would take 1 second … • For a problem size of 1000 with O(n 2) • For a problem size of 100 with O(n 3) • For a problem size of 20 with O(2 n) 23

Efficiency of Implementations of ADT List For array-based implementation • Add to end of list • Add to list at given position O(1) O(n) For linked implementation • Add to end of list • Add to list at given position • Retrieving an entry O(n)/O(1) O(n) 24

Comparing Implementations The time efficiencies of the ADT list operations for two implementations, expressed in Big Oh notation 25

Choose Implementation for ADT Consider the operations that your application requires A particular operation frequently, its implementation has to be efficient. Conversely, rarely use an operation, you can afford to use one that has an inefficient implementation. 26

Exercises Using Big Oh notation, indicate the time requirement of each of the following tasks in the worst case. Describe any assumptions that you make. a. After arriving at a party, you shake hands with each person there. b. Each person in a room shakes hands with everyone else in the room. c. You climb a flight of stairs. d. You slide down the banister. e. After entering an elevator, you press a button to choose a floor. f. You ride the elevator from the ground floor up to the nth floor. g. You read a book twice. 27

Exercises Suppose that your implementation of a particular algorithm appears in Java as follows: for (int pass = 1; pass <= n; pass++) { • • for (int index = 0; index < n; index++) { • for (int count = 1; count < 10; count++) • { . . . • } // end for • } // end for The algorithm involves an array of n items. The previous code shows the only repetition in the algorithm, but it does not show the computations that occur within the loops. These computations, however, are independent of n. What is the order of the algorithm? 28