The Efficiency of Algorithms Chapter 4 1 Adapted

The Efficiency of Algorithms Chapter 4 1 Adapted from Pearson Education, Inc.

Contents � Motivation � Measuring an Algorithm’s Efficiency � Counting Basic Operations � Best, Worst, and Average Cases � Big Oh Notation � The Complexities of Program Constructs � Picturing Efficiency � The Efficiency of Implementations of the ADT Bag � An Array-Based Implementation � A Linked Implementation � Comparing the Implementations 2 Adapted from Pearson Education, Inc.

Objectives � Assess efficiency of given algorithm � Compare expected execution times of two methods � Given 3 efficiencies of algorithms Adapted from Pearson Education, Inc.

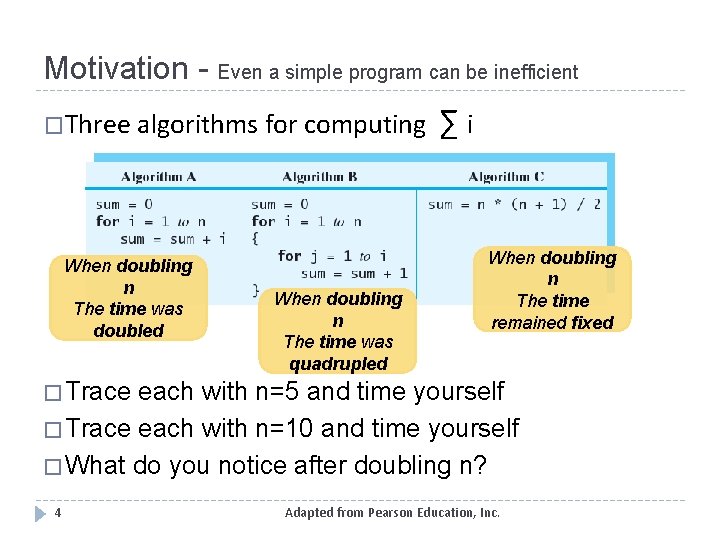
Motivation - Even a simple program can be inefficient �Three algorithms for computing When doubling n The time was doubled When doubling n The time was quadrupled ∑i When doubling n The time remained fixed � Trace each with n=5 and time yourself � Trace each with n=10 and time yourself � What do you notice after doubling n? 4 Adapted from Pearson Education, Inc.

Measuring an Algorithm’s Efficiency � Complexity � Space requirements � Time requirements � Other issues for best solution � Generality of algorithm � Programming effort � Problem size – number of items program will handle � Growth-rate function 5 Adapted from Pearson Education, Inc.

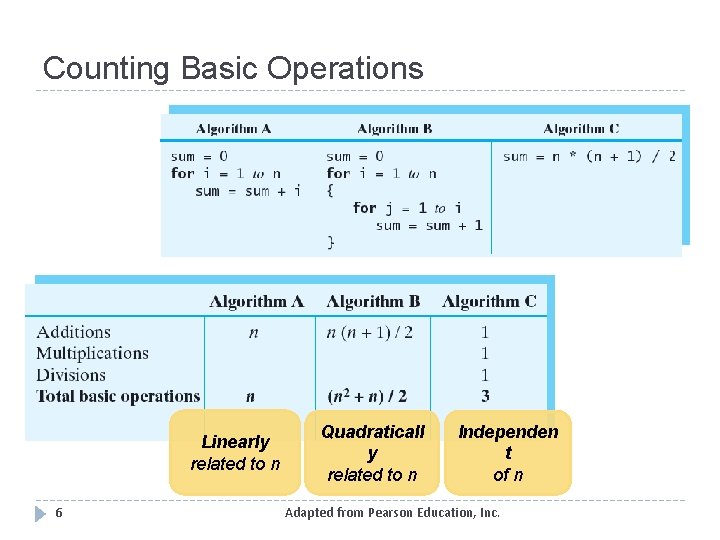
Counting Basic Operations Linearly related to n 6 Quadraticall y related to n Independen t of n Adapted from Pearson Education, Inc.

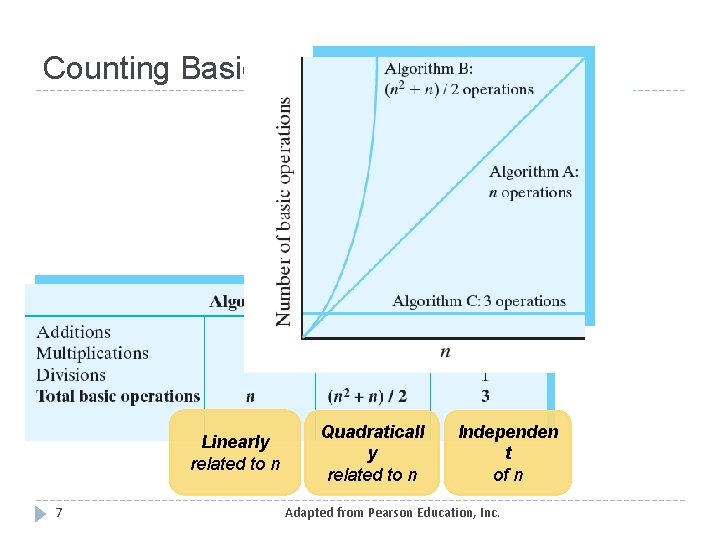
Counting Basic Operations Linearly related to n 7 Quadraticall y related to n Independen t of n Adapted from Pearson Education, Inc.

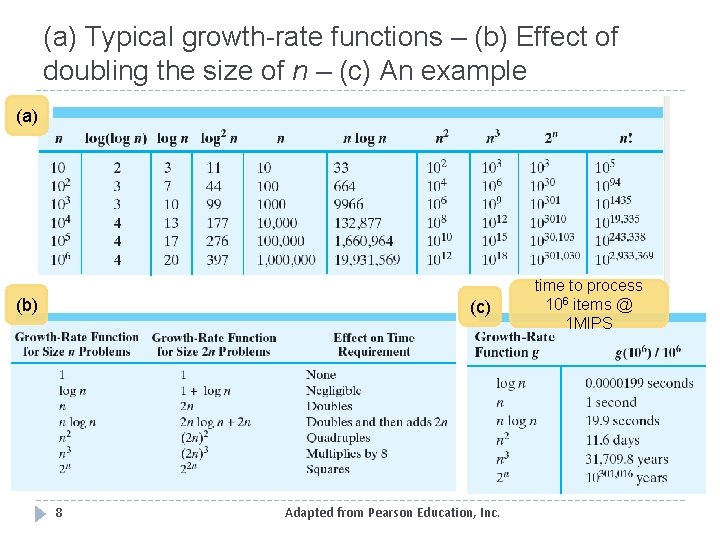
(a) Typical growth-rate functions – (b) Effect of doubling the size of n – (c) An example (a) (b) (c) 8 Adapted from Pearson Education, Inc. time to process 106 items @ 1 MIPS

Best, Worst, and Average Cases � Some algorithms depend only on size of data set � Other algorithms depend on nature of the data � Best case search when item at beginning � Worst case when item at end � Average case somewhere between 9 Adapted from Pearson Education, Inc.

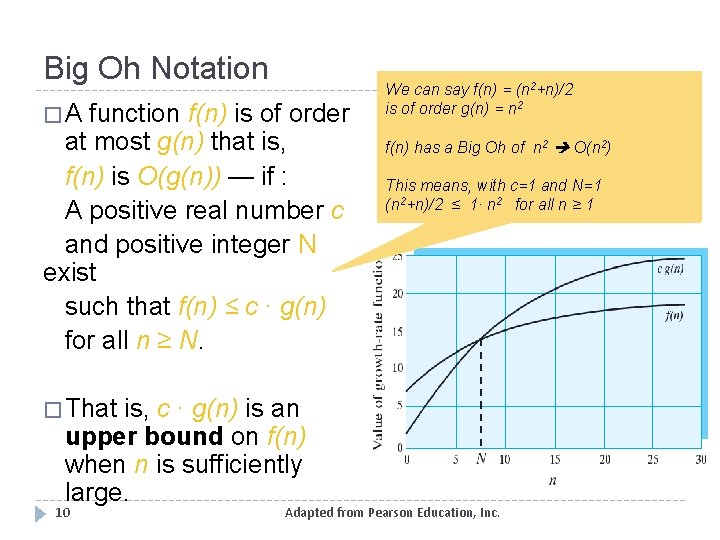
Big Oh Notation �A function f(n) is of order at most g(n) that is, f(n) is O(g(n)) — if : A positive real number c and positive integer N exist such that f(n) ≤ c ∙ g(n) for all n ≥ N. is, c ∙ g(n) is an upper bound on f(n) when n is sufficiently large. We can say f(n) = (n 2+n)/2 is of order g(n) = n 2 f(n) has a Big Oh of n 2 O(n 2) This means, with c=1 and N=1 (n 2+n)/2 ≤ 1∙ n 2 for all n ≥ 1 � That 10 Adapted from Pearson Education, Inc.

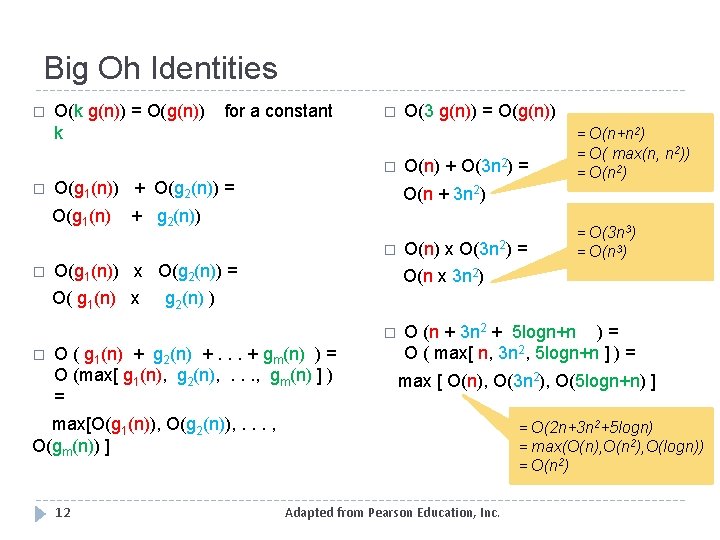
Big Oh Identities � O(k g(n)) = O(g(n)) for a constant k � O(g 1(n)) + O(g 2(n)) = O(g 1(n) + g 2(n)) � O(g 1(n)) x O(g 2(n)) = O(g 1(n) x g 2(n)) �O ( g 1(n) + g 2(n) +. . . + gm(n) )= O ( max[ g 1(n), g 2(n), . . . , gm(n) ] ) = max [ O(g 1(n)), O(g 2(n)), . . . , O(gm(n)) ] 11 Adapted from Pearson Education, Inc.

Big Oh Identities � O(k g(n)) = O(g(n)) k for a constant � � � O(g 1(n)) + O(g 2(n)) = O(g 1(n) + g 2(n)) O(g 1(n)) x O(g 2(n)) = O( g 1(n) x O(3 n 2) = g 2(n) ) O ( g 1(n) + g 2(n) +. . . + gm(n) ) = O (max[ g 1(n), g 2(n), . . . , gm(n) ] ) = O (n + 3 n 2 + 5 logn+n ) = O ( max[ n, 3 n 2, 5 logn+n ] ) = max [ O(n), O(3 n 2), O(5 logn+n) ] max[O(g 1(n)), O(g 2(n)), . . . , O(gm(n)) ] 12 = O(3 n 3) = O(n 3) O(n x 3 n 2) � � O(n) + O(3 n 2) = = O(n+n 2) = O( max(n, n 2)) = O(n 2) O(n + 3 n 2) � � O(3 g(n)) = O(2 n+3 n 2+5 logn) = max(O(n), O(n 2), O(logn)) = O(n 2) Adapted from Pearson Education, Inc.

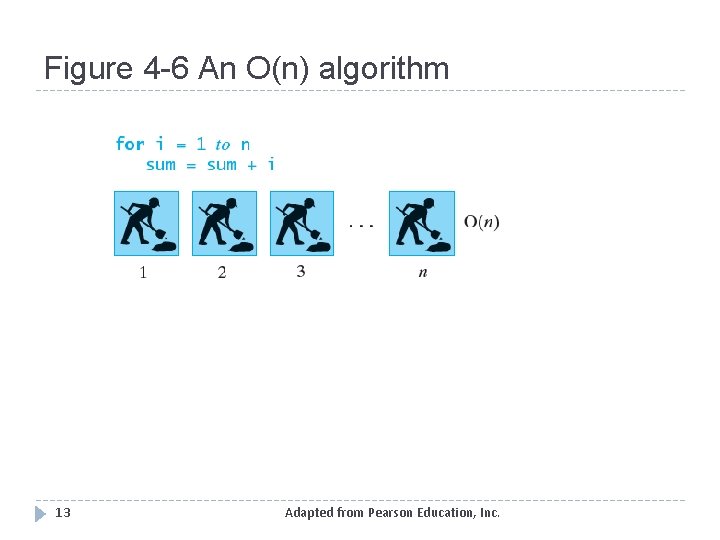
Figure 4 -6 An O(n) algorithm 13 Adapted from Pearson Education, Inc.

Figure 4 -7 An O(n 2) algorithm 14 Adapted from Pearson Education, Inc.

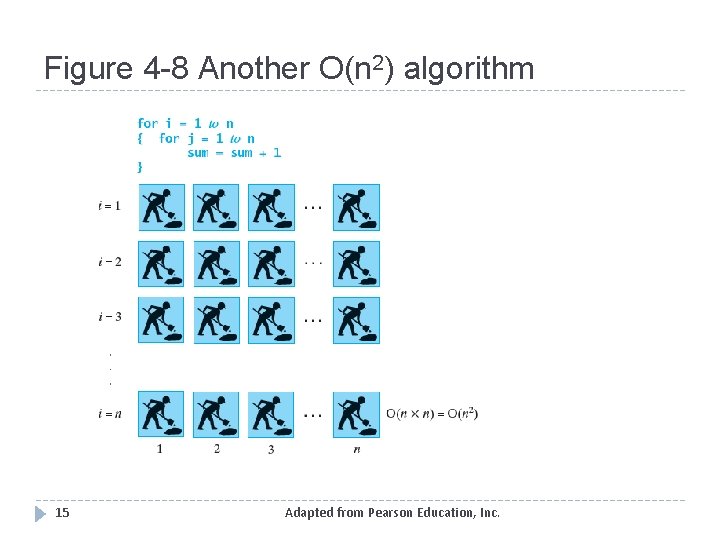
Figure 4 -8 Another O(n 2) algorithm 15 Adapted from Pearson Education, Inc.

Complexities of program constructs Construct � Consecutive Time Complexity segments � Add growth-rates max � If that choses between if -part and else-part �A loop that iterates m times � O(cond) + max(O(if-part), O(elsepart)) �m 16 * (O(cond) + O(body)) Adapted from Pearson Education, Inc.

Array Based Implementation (fixed size) � Adding 17 an entry to a bag, an O(1) method, Adapted from Pearson Education, Inc.

Array Based Implementation (fixed size) � Adding an entry to a bag, an O(1) method, O(1) Max(O(1), O(1)) = O(1) +O(1) = O(1) 18 Adapted from Pearson Education, Inc. O(1) +O(1) = O(1)

Array Based Implementation � Searching for an entry, O(1) best case, O(n) worst or average case O(n) method overall 19 Adapted from Pearson Education, Inc.

Array Based Implementation � Searching for an entry, O(1) best case, O(n) worst or average case O(n) method overall The size of the bag, is the size of the problem number. Of. Entries is our n This loop executes number. Of. Entries times, i. e. n times O(1) O(1) +O(1) =O(1) n * (O(1) + O(1)) = n * O(1) = O(n) O(1) 20 Adapted from Pearson Education, Inc. O(1) +O(n) +O(1) = O(n)

A Linked Implementation � Adding an entry to a bag, an O(1) method, O(1) +O(1) = O(1) 21 Adapted from Pearson Education, Inc.

A Linked Implementation � Searching a bag for a given entry, O(1) best case, O(n) worst case O(n) overall 22 Adapted from Pearson Education, Inc.

A Linked Implementation � Searching a bag for a given entry, O(1) best case, The size of the bag, is the size of the O(n) worst case O(n) overall problem This loop executes n times O(1) n * (O(1)+O(1)) = n * O(1) = O(n) O(1) 23 Adapted from Pearson Education, Inc. O(1) +O(n) +O(1) = O(n)

Time efficiencies of the ADT bag operations 24 Adapted from Pearson Education, Inc.

End Chapter 4 25 Adapted from Pearson Education, Inc.