The Edge Randomized Algorithms for Network Monitoring George

The Edge --- Randomized Algorithms for Network Monitoring George Varghese Oct 14, 2009

Research motivation The Internet in 1969 The Internet today Problems Flexibility, speed, scalability Overloads, attacks, failures Measurement & control Ad-hoc solutions suffice Engineered solutions needed This talk: using randomized algorithms in network chips for monitoring performance and security in routers

Focus on 3 Monitoring Problems l l l Problem 1: Finding heavy-bandwidth flows Problem 2: Measuring usec network latencies Problem 3: Logging all infected nodes during an attack with limited memory In each case, a simple “sampling” scheme works But in each case, if the router can add some memory and processing, we can get an edge. . .

Get edge subject to constraints l l Low memory: On-chip SRAM limited to around 32 Mbits. Not constant but is not scaling with number of concurrent conversations/packets Small processing: For wire-speed at 40 Gbps, using 40 byte packets, have 8 nsec. Using 1 nsec SRAM, 8 memory accesses. Factor of 30 in parallelism buys 240 accesses.

Problem 1: Heavy-bandwidth users Heavy-hitters: In a measurement interval, (e. g. , 1 minute) me S 2 S 6 S 2 S 5 S 1 S 2 Source S 2 is 30 percent of traffic sequence Estan, Varghese, ACM TOCS 2003

Getting an Edge for heavy-hitters l l Sample: Keep a M size sample of packets. Estimate heavy-hitter traffic from sample Sample and Hold: Sampled sources held in a CAM of size M. All later packets counted Edge: Standard error of bandwidth estimate is O(1/M) for S&H instead of O(1/sqrt(M)) Improvement: (Prabhakar et al): Periodically remove “mice” from “elephant trap”

Problem 2: Fine-Grain Loss and Latency Measurement (with Kompella, Levchenko, Snoeren) SIGCOMM 2009, to appear

Fine-grained measurement critical l Delay and loss requirements have intensified: u Automated financial programs » < 100 usec latency, very small (1 in 100, 000) loss? u High-performance computing, data centers, SANs » < 10 usec, very small loss l New end-to-end metrics of interest u u u Average delay (accurate to < msec, possibly microsecs) Jitter (delay variance helps) Loss distribution (random vs microbursts, TCP timeouts)

Existing router infrastructure l SNMP (simple aggregate packet counters) u l Coarse throughput estimates not latency Net. Flow (packet samples) u Need to coordinate samples for latency. Coarse

Applying existing techniques l Standard approach is active probes and tomography u u l Join results from many paths to infer per-link properties Can be applied to measuring all the metrics of interest Limitations u Overheads for sending probes limits granularity » Cannot be used to measure latencies < 100’s of μsecs u Tomography inaccurate due to under-constrained formulation

Our approach l Add hardware to monitor each segment in path u u u Use a low-cost primitive for monitoring individual segments Compute path properties through segment composition Ideally, segment monitoring uses few resources » Maybe even cheap enough for ubiquitous deployment! l This talk shows our first steps u u u Introduce a data structure called an LDA as key primitive We’ll use a only small set of registers and hashing Compute loss, delay average and variance, loss distribution We measure real traffic as opposed to injected probes

Outline l Model l Why simple data structures do not work l LDA for average delay and variance

Abstract segment model l DR R to S is considered separately Interval depends on granularity required (typically sub-second) Both S and R maintain some state D about packets u l DS Divide time into equal bins (measurement intervals) u l Receiver R Packets always travel from S to R u l Sender S State is updated upon packet departure S transmits DS to R u R computes the required metric as f(DS , DR)

Assumptions Sender S l l Receiver R Assumption 1: FIFO link between sender and receiver Assumption 2: Fine-grained per-segment time synchronization u Using IEEE 1588 protocol, for example l Assumption 3: Link susceptible to loss as well as variable delay Assumption 4: A little bit of hardware can be put in the routers l You may have objections, we will address common ones later l

Constraints Sender S Receiver R l Constraint 1: Very little high-speed memory Constraint 2: Limited measurement communication budget Constraint 3: Constrained processing capacity l Consider a run-of-the-mill OC-192 (10 -Gbps) link l l u u 250 -byte packets implies 5 million packets per second At most 1 control packet every msec, more likely once per sec

Computing loss Sender S Receiver R 1 32 12 counter l l l Loss = 3– 2=1 Store a packet counter at S and R. S sends the counter value to R periodically R computes loss by subtracting its counter value from S’s counter

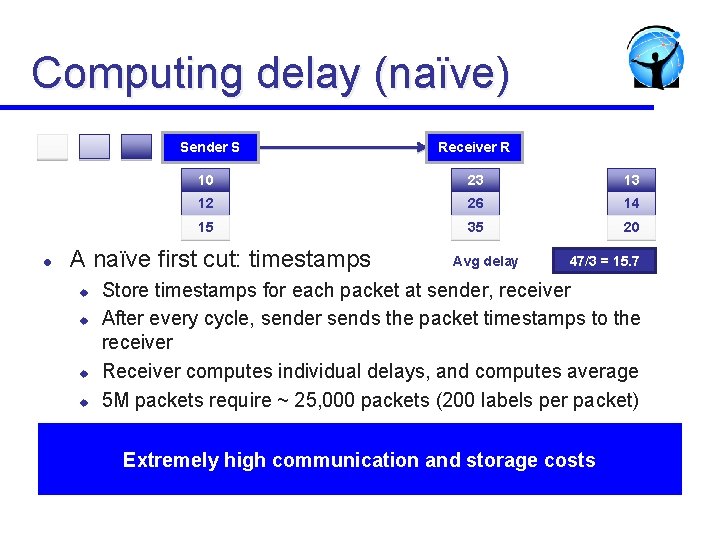
Computing delay (naïve) Sender S l 10 23 13 12 26 14 15 35 20 A naïve first cut: timestamps u u Receiver R Avg delay 47/3 = 15. 7 Store timestamps for each packet at sender, receiver After every cycle, sender sends the packet timestamps to the receiver Receiver computes individual delays, and computes average 5 M packets require ~ 25, 000 packets (200 labels per packet) Extremely high communication and storage costs

Computing delay (sampled) Sender S Receiver R 10 23 13 15 35 20 Avg delay l 33/2 = 16. 5 (Slightly) better approach: sampling u Store timestamps for only sampled packets at sender, receiver u 1 in 100 sampling means ~ 250 packets Less expensive, but we can get an edge. . .

Delay with no packet loss Sender S Receiver R 10+12+15 23+26+35 counter Avg delay l Observation: Aggregation can reduce cost u u Store sum of the timestamps at S & R After every cycle, S sends its sum CS to R R computes average delay as (CS – CR) / N Only one counter and one packet to send Works great, if packets were never lost… 84 -37/3 = 15. 7

Delay in the presence of loss l l l Consider two packets, first sent at T/2 and lost. Second sent at T, received at T. Receiver gets D = T/4 Lost packets can cause Error = O(T) where T is the size of the measurement interval Failed quick fix: Bloom filter will not work u Always a finite false positive probability

Theory Perspective: Streaming l l Streaming algorithms a massive field of study in theory, databases, and web analysis However, our problem has two big differences: u u l Coordination: Instead of calculating F(s_i) on one stream s_i. we compute F(s_i, r_i) on two streams s_i and r_i Loss: Some of the r_i can be undefined because of loss Example: Max is trivial in streaming setting but provably requires linear memory in coordinated setting

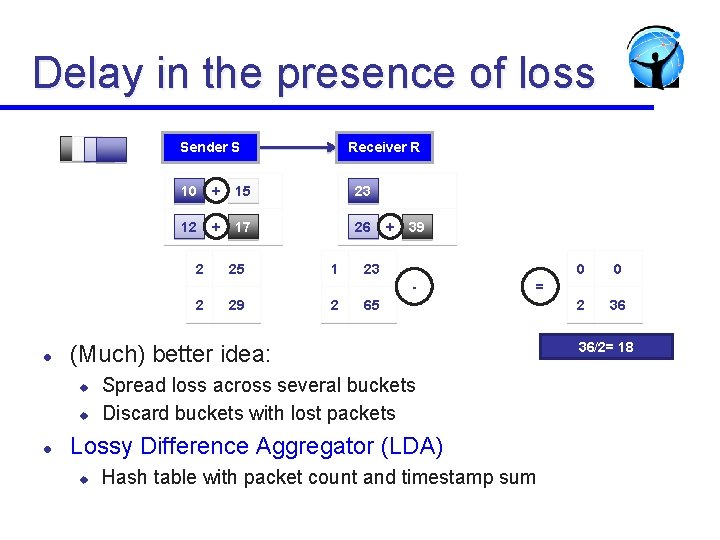
Delay in the presence of loss Sender S Receiver R 10 + 15 23 12 + 17 26 2 25 1 + 39 23 - 2 l 2 u 65 Spread loss across several buckets Discard buckets with lost packets Lossy Difference Aggregator (LDA) u 0 2 36 = (Much) better idea: u l 29 0 Hash table with packet count and timestamp sum 36/2= 18

Analysis and Refinements l Packet loss u u l l Problem: High loss implies many bad buckets Solution: Sampling u l l k packet losses can corrupt up to k buckets If k << B, then only a small subset of buckets corrupted Control sampling rate such that no more than B/2 buckets corrupted (based on loss rate) Problem: Loss rate is unpredictable Solution: Run parallel copies for several loss rates u Logarithmic copies suffice in theory, smaller in practice

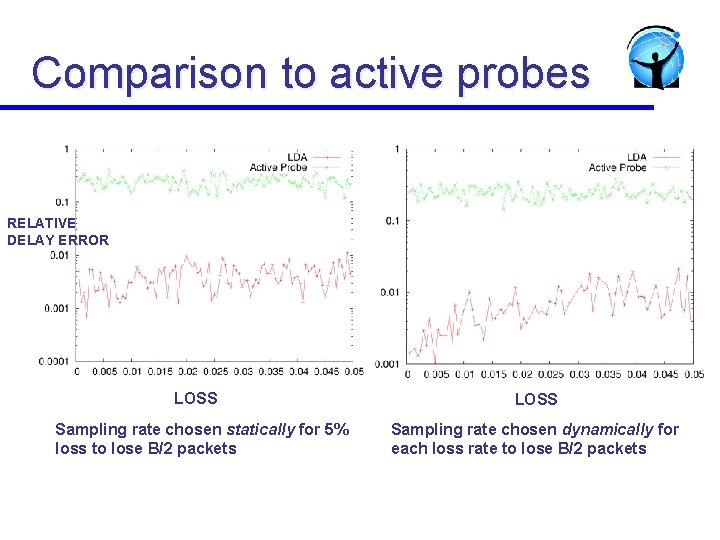
Comparison to active probes RELATIVE DELAY ERROR LOSS Sampling rate chosen statically for 5% loss to lose B/2 packets LOSS Sampling rate chosen dynamically for each loss rate to lose B/2 packets

Computing jitter l l l Propose measuring jitter as variance in delay Can we adapt LDA to measure variance ? Solution idea: inspired by sketching [AMS 96] u Consider random variable Xi that takes values +1 and -1 with probability ½ u At S and R, packet pi has timestamps ai and bi u S transmits ∑ai*Xi to R 2 2 u R computes (∑bi*Xi - ∑ai*Xi) / n - µ to obtain variance

Why this works (AMS 96) =1 =0

Other issues l l Implementation: counters plus increment/decrement. 200 SRAM counters < 1% of 95 nm ASIC FIFO model: load balancing breaks model, need to enforce by doing on each link in hunt group Deployment: deploy within single router first using flow through logic: majority of loss, delay within routers Time synchronization: being done within routers, also across links with IEEE 1588 and GPS (Corvil)

Summary of Problem 2 l l With rise in modern trading and video applications, fine grained latency is important. Active probes cannot provide latencies down to microseconds Proposed LDAs for performance monitoring as a new synopsis data structure u Simple to implement and deploy ubiquitously u Capable of measuring average delay, variance, loss and possibly detecting microbursts u Edge is N samples (1 million) versus M samples (1000) for no-error case. Reduces error by 300.

Carousel --- Scalable and (nearly) complete collection of Information Terry Lam (with M. Mitzenmacher and G. Varghese, NSDI 2009)

Data deluge in Networks Denial of Service l l l Worm outbreak Millions of potentially interesting events How to get a coherent view despite bandwidth and memory limits? Standard solutions: sampling and summarizing 30

What if you want complete collection? l l Need to collect infected stations for remediation Other examples of complete collection: u List all IPv 6 stations u List all MAC addresses in a LAN 31

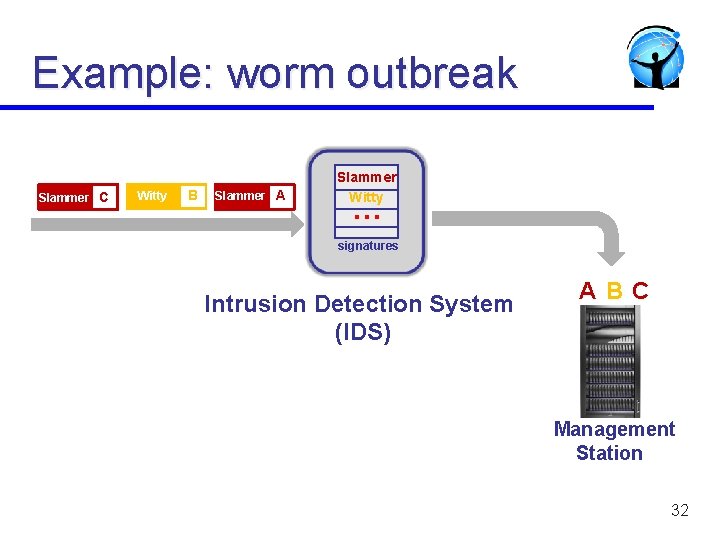
Example: worm outbreak Slammer C Witty B Slammer A Slammer Witty … signatures Intrusion Detection System (IDS) A BC Management Station 32

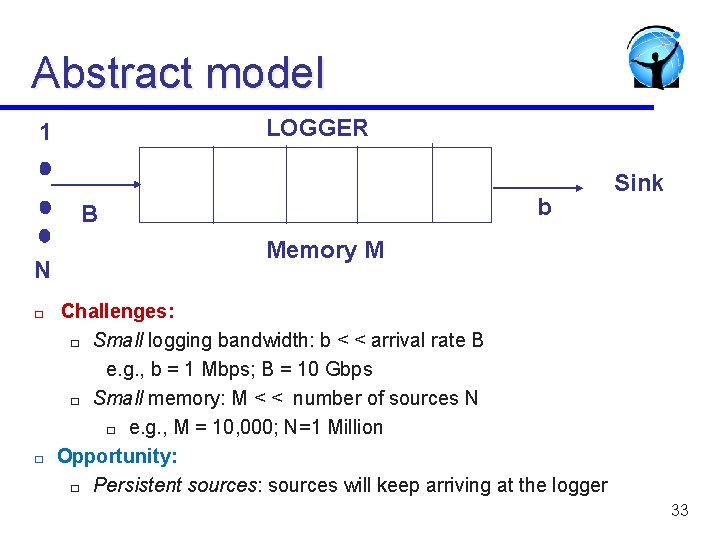
Abstract model LOGGER 1 b B N � � Sink Memory M Challenges: � Small logging bandwidth: b < < arrival rate B e. g. , b = 1 Mbps; B = 10 Gbps � Small memory: M < < number of sources N � e. g. , M = 10, 000; N=1 Million Opportunity: � Persistent sources: sources will keep arriving at the logger 33

Our results l l Carousel: new scheme, with minimal memory can log almost all sources in close to optimal time (N/b) Standard approach is much worse u ln(N) times worse in an optimistic random model u Adding a Bloom filter does not help u Infinitely worse in a deterministic adversarial model 34

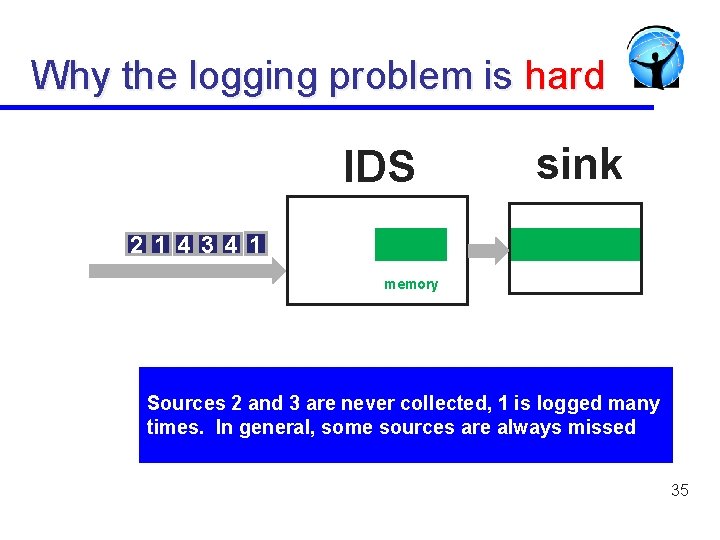
Why the logging problem is hard IDS sink 2 1 4 3 4 1 memory Sources 2 and 3 are never collected, 1 is logged many times. In general, some sources are always missed 35

Why the problem is still hard with a Bloom filter IDS 2 14214 3 4 1 sink 4 1 memory Bloom filter l Similar performance to a standard logger u Again, sources 2 and 3 are never collected because of timing Bloom filter is necessarily small (M) compared to sources (N) 36

Congestion Control for Logging? l l Random dropping leads to congestion collapse Standard solution: closed loop congestion (TCP) and admission control: but needs cooperative sources What can a poor resource do to protect itself unilaterally without cooperation from senders? Our approach: Randomized Admission Control. u Break sources into random groups and “admit” one group at a time for logging

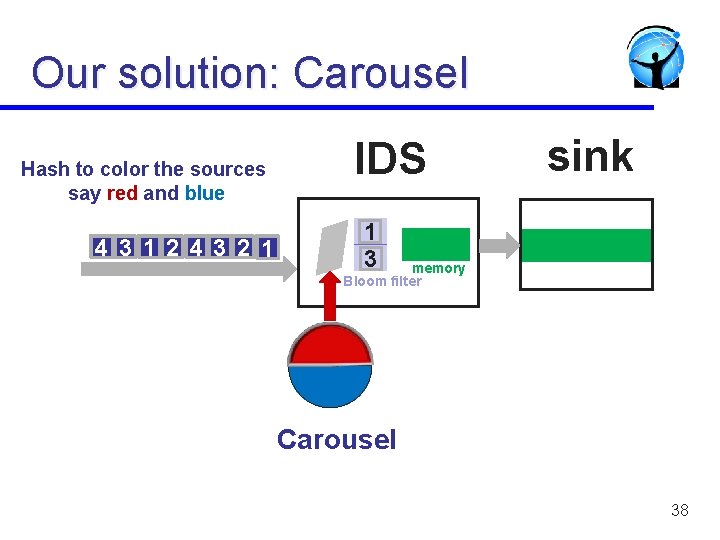
Our solution: Carousel Hash to color the sources say red and blue 4 3 1 2 4 3 2 1 IDS sink 1 3 memory Bloom filter Carousel 38

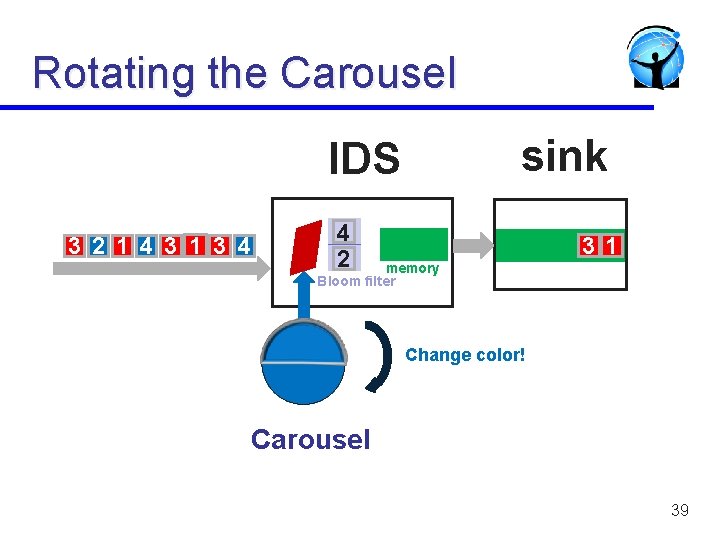
Rotating the Carousel sink IDS 3 2 1 4 3 1 3 4 4 2 31 memory Bloom filter Change color! Carousel 39

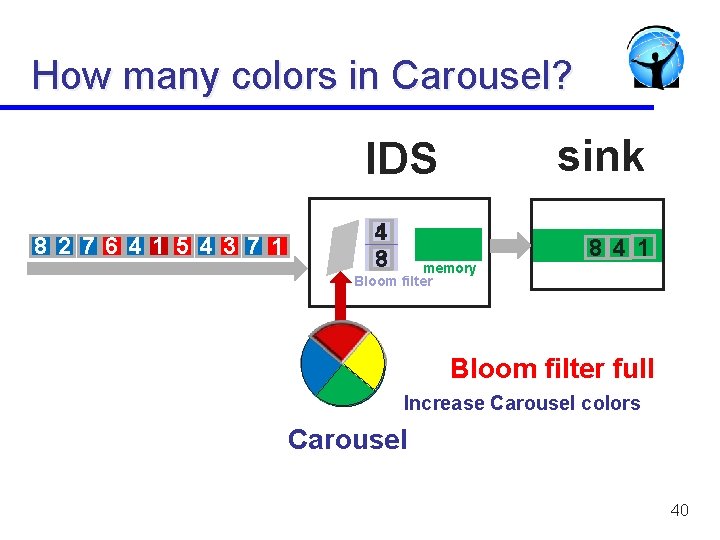
How many colors in Carousel? sink IDS 8 2 7 6 4 1 5 4 3 7 1 4 1 8 3 memory Bloom filter 8 4 1 Bloom filter full Increase Carousel colors Carousel 40

Summary of Carousel algorithm l Partition u u l Iterate u u u l Hk(X): lower k bits of H(S), a hash function of a source S Divide the population into partitions with same hash value T = M / b (available memory divided by logging bandwidth) Each phase last T seconds, corresponds a distinct hash value Bloom filter weeds out duplicates within a phase Monitor u Increase or decrease k to control the partition size 41

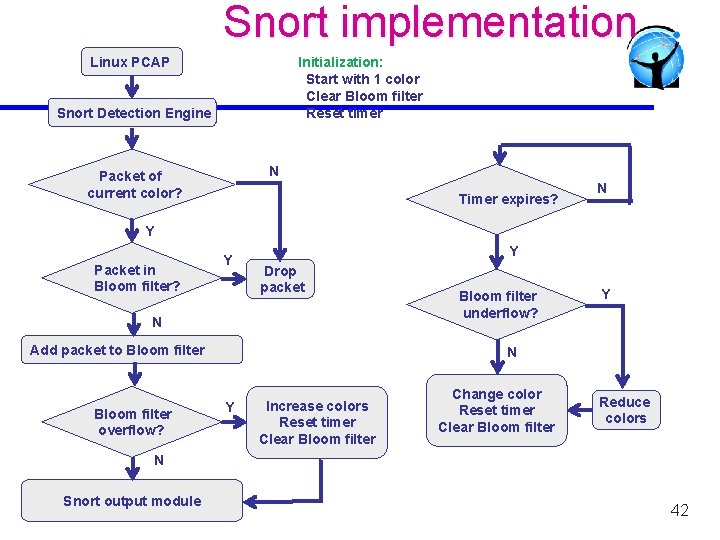
Snort implementation Linux PCAP Initialization: Start with 1 color Clear Bloom filter Reset timer Snort Detection Engine N Packet of current color? Timer expires? N Y Packet in Bloom filter? Y Y Drop packet N Add packet to Bloom filter overflow? Bloom filter underflow? Y N Y Increase colors Reset timer Clear Bloom filter Change color Reset timer Clear Bloom filter Reduce colors N Snort output module 42

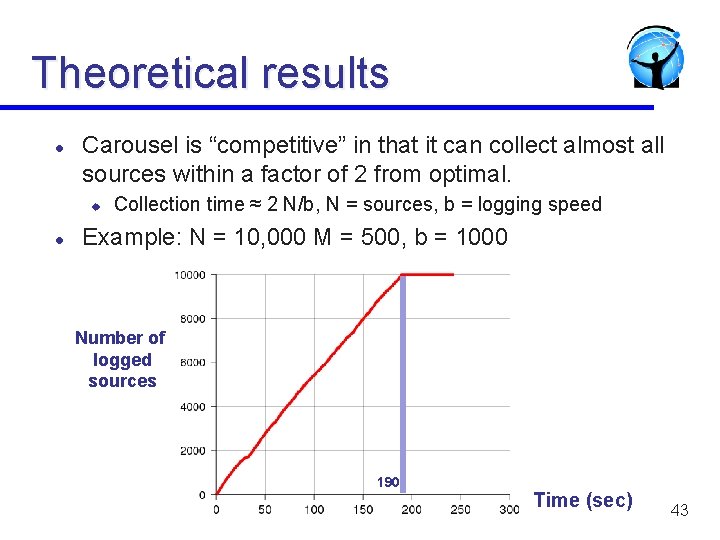
Theoretical results l Carousel is “competitive” in that it can collect almost all sources within a factor of 2 from optimal. u l Collection time ≈ 2 N/b, N = sources, b = logging speed Example: N = 10, 000 M = 500, b = 1000 Number of logged sources 190 Time (sec) 43

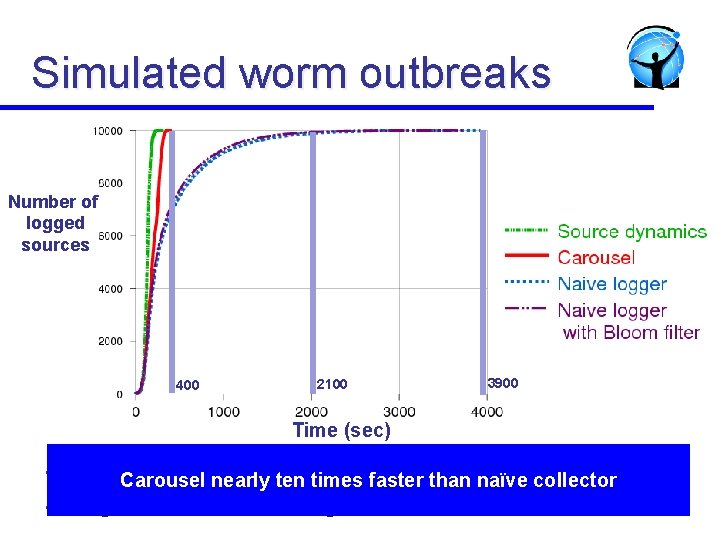
Simulated worm outbreaks Number of logged sources 400 2100 3900 Time (sec) l l N = 10, 000; M = 500; b = 100 items/sec Carousel nearly ten times faster than naïve collector Logistic model of worm growth 44

Snort Experimental Setup l l Scaled down from real traffic: 10, 000 sources, buffer of 500, input rate =100 Mbps, logging rate = 1 Mbps Two cases: source S picked randomly on each packet or periodically (1, 2, 3. . 10, 000, 1, 2, 3, . . )

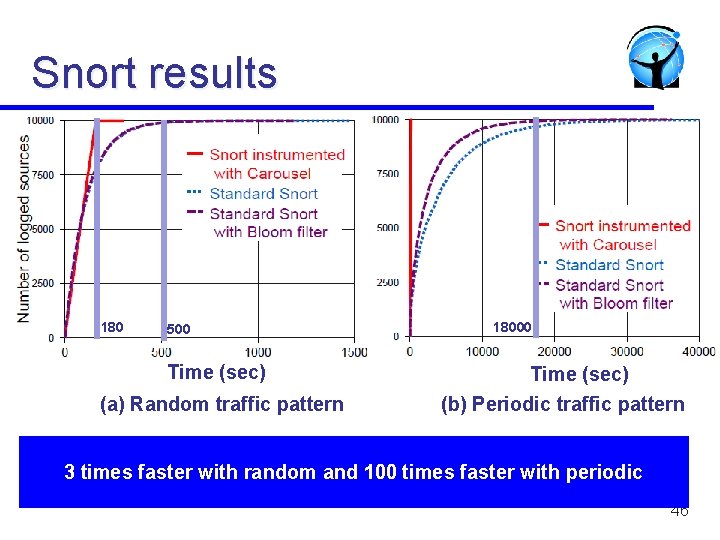
Snort results 180 500 Time (sec) (a) Random traffic pattern 18000 Time (sec) (b) Periodic traffic pattern 3 times faster with random and 100 times faster with periodic 46

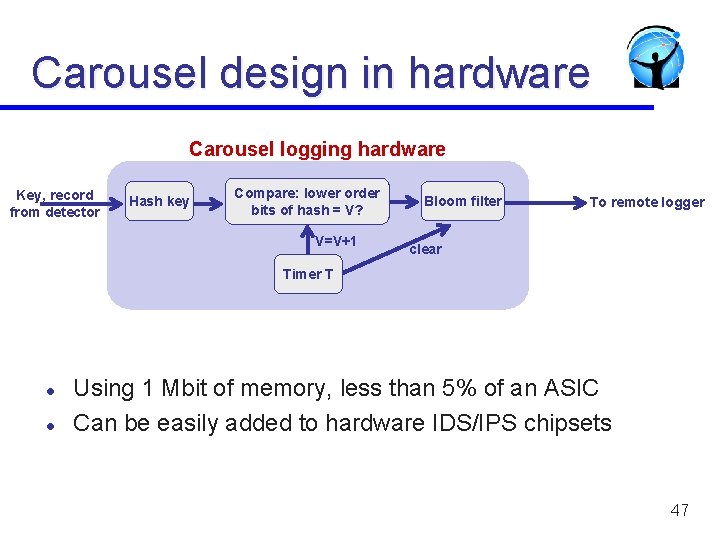
Carousel design in hardware Carousel logging hardware Key, record from detector Hash key Compare: lower order bits of hash = V? V=V+1 Bloom filter To remote logger clear Timer T l l Using 1 Mbit of memory, less than 5% of an ASIC Can be easily added to hardware IDS/IPS chipsets 47

Related work l High speed implementations of IPS devices u u l Fast reassembly, normalization and regular expression No prior work on scalable logging Alto file system: dynamic and random partitioning u u Fits big files into small memory to rebuild file index after crash Memory is only scarce resource Carousel handles both limited memory and logging speed Carousel has a rigorous competitive analysis 48

Limitations of Carousel l Carousel is probabilistic: sources can be missed with low probability mitigate by changing hash function on each Carousel cycle. Carousel relies on a “persistent source assumption” u Does not guarantee logging of “one-time” events Carousel does not prevent duplicates at the sink but has fast collection time even in an adversarial model. 49

Conclusions l Carousel is a scalable logger that u u u l Collects nearly all persistent sources in nearly optimal time Is easy to implement in hardware and software Is a form of randomized admission control Applicable to a wide range of monitoring tasks with: u u High line speed, low memory, and small logging speed And where sources are persistent 50

Edge can be an order of magnitude l l l RAC is factor of 2 off from optimal to log all sources versus ln N/M off for naïve. u For N = 1 million and M small, edge is close to 14 for random arrivals; infinite for worst-case LDA offers N samples versus M samples for naïve ‘ u For N = 1 million, M = 10, 000, edge is close to 10 Sample and Hold offers O(1/M) standard error versus O(1/sqrt(M)) for naïve u For M = 10, 000, edge in standard error is 100

Related Work l l LDA: u Streaming Algorithms: less work on 2 -party streaming algorithms between a sender and receiver u Network tomography: joins the result of black box measurements to infer link delays and losses RAC: u Random partitions a common idea. We apply to admission control and add cycling through partitions u Alto Scavenger “discards information for half the files” if disk full

Summary l l l Monitoring networks for performance problems and security at high speeds is important but hard Randomized streaming algorithms can offer cheaper (in gates) solutions at high speeds. Described two simple randomized algorithms u LDA: Aggregate by summing, hash to withstand loss u RAC: Randomly partition input into small enough sets. Cycle through sets for fairness.

In conclusion. . . The Edge

l Venky: some renewal assumptions needed. Can estimate renewal times by sampling someone in each sampling group (real ID) and storing arrival timestamp and seeing how long it takes to return. Keep a few samples each time. Why sample. Why not take first few. May have bias/ Have two classes. Slow and fast. In that case sample a few randomly in class when a new one comes in (1 in M probability). Then watch him across intervals. Start with large interval and reduce. Too conservative T will lead to large overstimates N/M * T, if T is twice as large as real renewal time, then time is doubled over optimal

Detecting microbursts l l μbursts are defined as series of closely spaced losses Adapting LDA for detecting microbursts u Buckets with no packet lost » ∑bi - ∑ai ≈ n x μ, ai and bi are the timestamps at S and R u Buckets with exactly one packet lost (say al ) » ∑bi - ∑ai ≈ n x μ - al u u u l Timestamp of lost packet ≈ n x μ – (∑bi - ∑ai) Compute for all single loss buckets in LDA If all these timestamps “close” together, then μburst Use enough buckets so each <= single loss w. h. p. u Can obtain confidence bounds using Hoeffding’s inequality