The Distance to the Stars Angular Separation is








- Slides: 14

The Distance to the Stars! • Angular Separation is not enough! • We want to know the answer to the ‘age old question’: How far away are the stars? Ans: A lot farther than anyone imagined! See: “Parallax” by Alan Hirshfeld

How far away are the Stars?

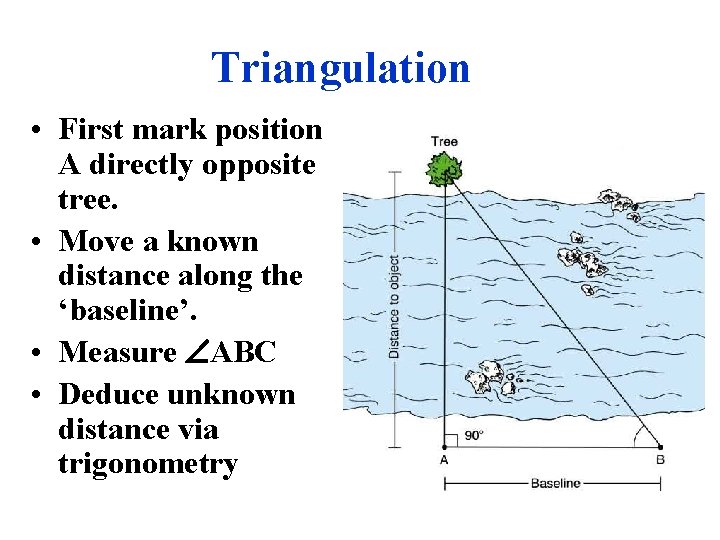
Triangulation • First mark position A directly opposite tree. • Move a known distance along the ‘baseline’. • Measure ABC • Deduce unknown distance via trigonometry

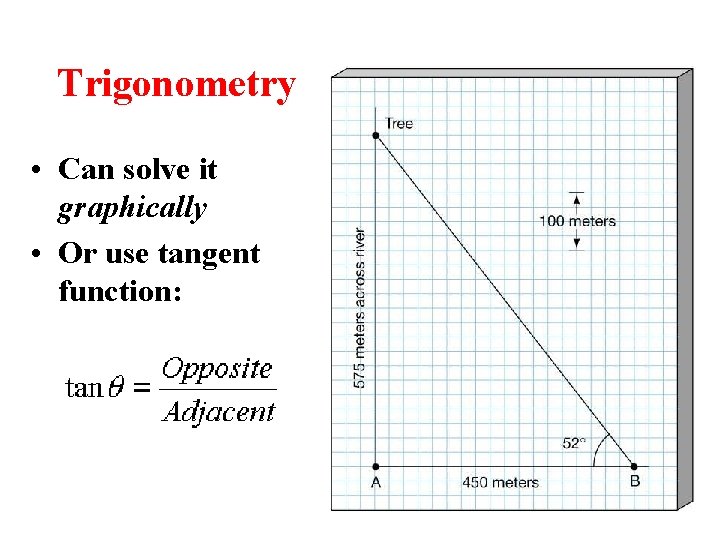
Trigonometry • Can solve it graphically • Or use tangent function:

Parallax • Consider a planet as seen against the background stars (very far away). • View from A and B are different –the planet moves with respect to the background stars • Apparent angular displacement is Parallax.

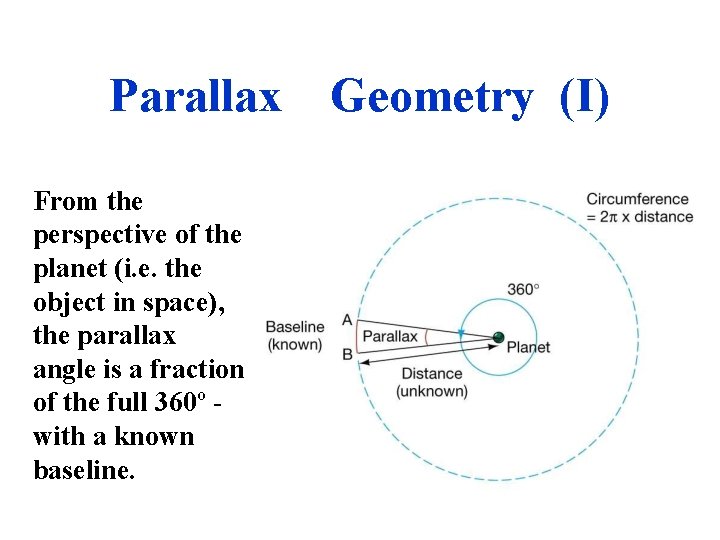
Parallax Geometry (I) From the perspective of the planet (i. e. the object in space), the parallax angle is a fraction of the full 360º with a known baseline.

Parallax and Baselines 2 Observers 1000 km apart determine the Moon’s parallax to be 9. 0' = 0. 15

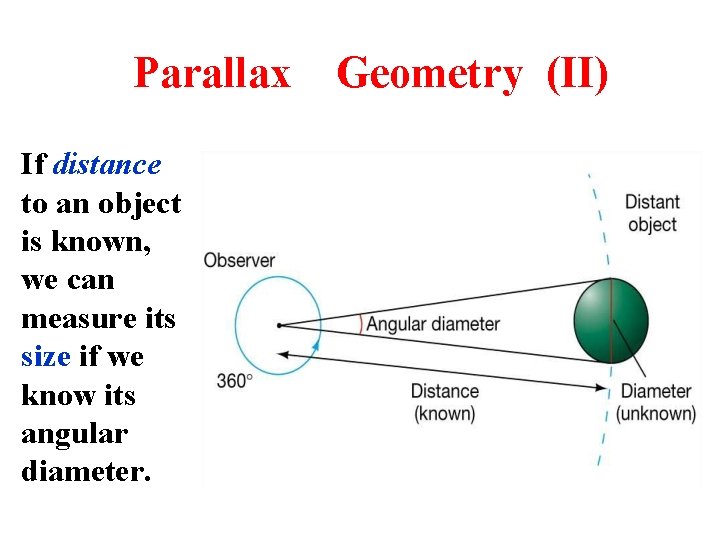
Parallax Geometry (II) If distance to an object is known, we can measure its size if we know its angular diameter.

Determination of Size • If distance to an object is known, we can measure its size. • Moon’s angular diameter is 31' = 0. 52 • Diameter of Earth is ~12800 km

Technical Difficulties in Triangulation • For a fixed baseline, angle 90 as object gets further away. • Hence error in distance value increases. • How big a baseline can you get? Diameter of Earth : 13, 000 km Size of Earth’s orbit : 300, 000 km

Parallax Angle is Small! • The closer the object the larger the parallax. • Parallaxes are usually very small. Parallax of Venus at closest approach (45 million km) is 1 arc minute! • Parallax of nearby (25 light years) stars not observed/measured until 1839!

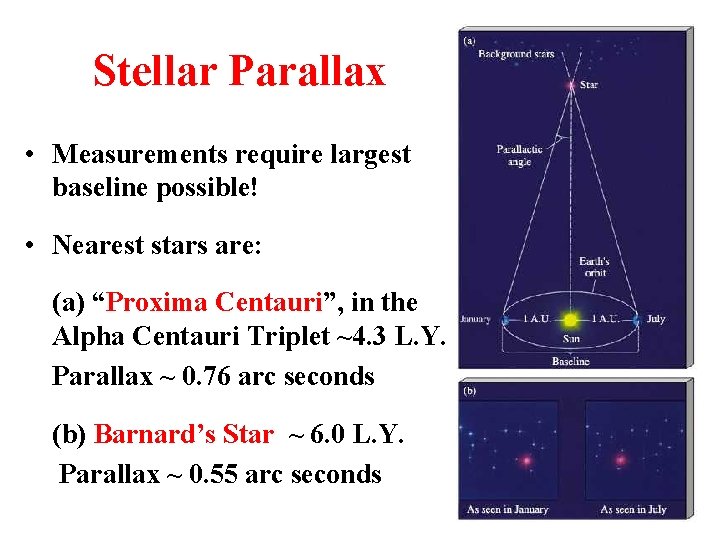
Stellar Parallax • Measurements require largest baseline possible! • Nearest stars are: (a) “Proxima Centauri”, in the Alpha Centauri Triplet ~4. 3 L. Y. Parallax ~ 0. 76 arc seconds (b) Barnard’s Star ~ 6. 0 L. Y. Parallax ~ 0. 55 arc seconds

Distance Scale! • Proxima Centauri ~ 4. 3 L. Y • Barnard’s Star ~ 6. 0 L. Y. If the earth was a grain of sand orbiting a small marble-sized Sun with a radius of 1 m, then Proxima Centauri would be 270 km away! Barnard’s Star would be 370 km away!

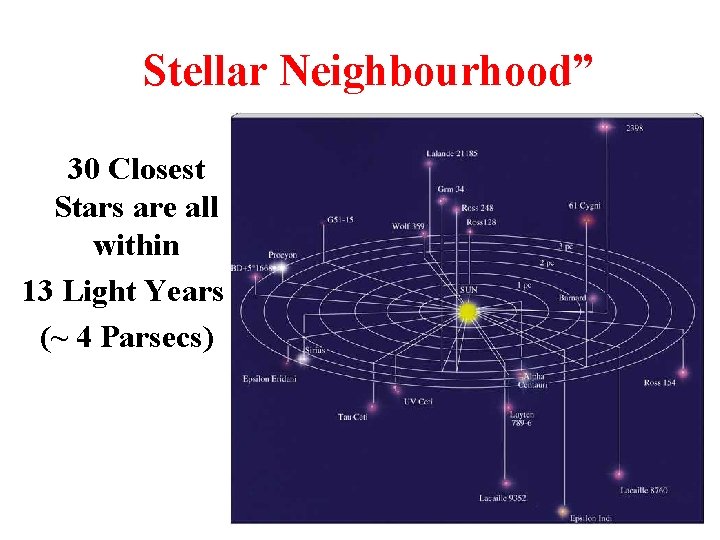
Stellar Neighbourhood” 30 Closest Stars are all within 13 Light Years (~ 4 Parsecs)