The Discriminant and Quadratic Formula MM 2 A

  • Slides: 11
Download presentation
The Discriminant and Quadratic Formula MM 2 A 4. Students will solve quadratic equations

The Discriminant and Quadratic Formula MM 2 A 4. Students will solve quadratic equations and inequalities in one variable. b. Find real and complex solutions of equations by factoring, taking square roots, and applying the quadratic formula. c. Analyze the nature of roots using technology and using the discriminant.

What is the discriminant? 2 The discriminant is the expression b – 4 ac.

What is the discriminant? 2 The discriminant is the expression b – 4 ac. The value of the discriminant can be used to determine the number and type of roots of a quadratic equation.

If the value of the discriminant is positive, the equation will have 2 real

If the value of the discriminant is positive, the equation will have 2 real solutions. If the value of the discriminant is a perfect square, the roots will be rational (no square roots). If it’s not a perfect square, you will have a square root in your solutions

If the value of the discriminant is zero, the equation will have 1 real

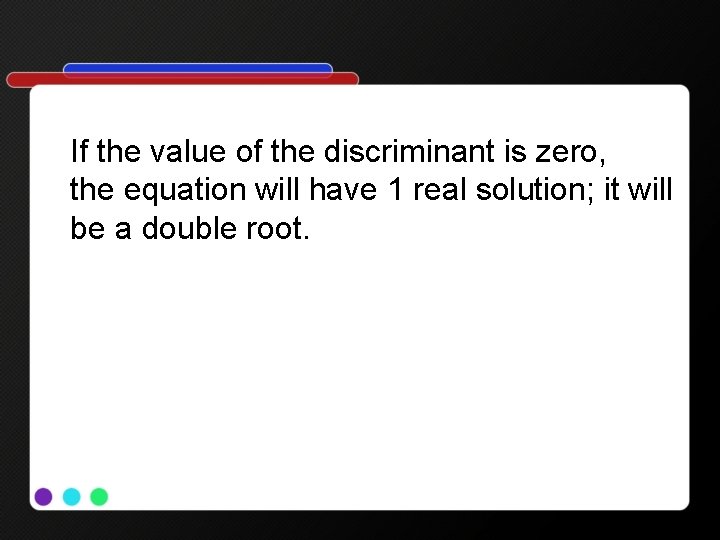
If the value of the discriminant is zero, the equation will have 1 real solution; it will be a double root.

If the value of the discriminant is negative, the equation will have 2 complex

If the value of the discriminant is negative, the equation will have 2 complex roots; they will be complex conjugates.

Let’s put all of that information in a chart. Value of Discriminant Type and

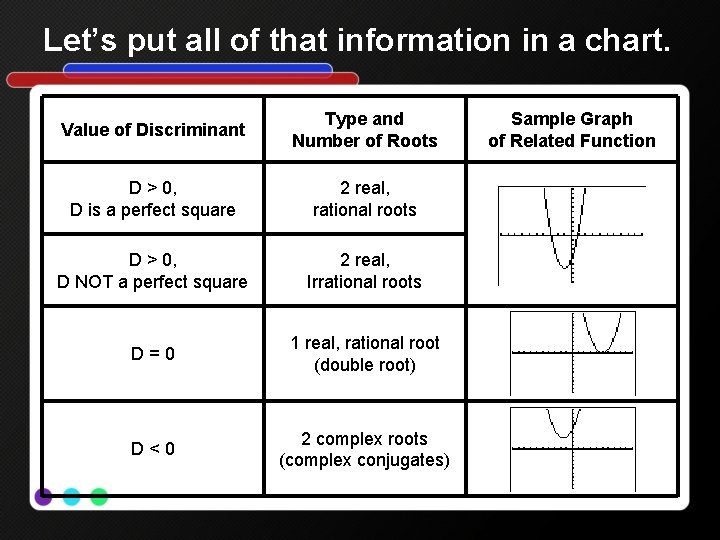
Let’s put all of that information in a chart. Value of Discriminant Type and Number of Roots D > 0, D is a perfect square 2 real, rational roots D > 0, D NOT a perfect square 2 real, Irrational roots D=0 1 real, rational root (double root) D<0 2 complex roots (complex conjugates) Sample Graph of Related Function

Try These. For each of the following quadratic equations, a) Find the value of

Try These. For each of the following quadratic equations, a) Find the value of the discriminant, and b) Describe the number and type of roots. 1. x 2 + 14 x + 49 = 0 3. 3 x 2 + 8 x + 11 = 0 2. x 2 + 5 x – 2 = 0 4. x 2 + 5 x – 24 = 0

The Answers 1. x 2 + 14 x + 49 = 0 D=0 1

The Answers 1. x 2 + 14 x + 49 = 0 D=0 1 real, rational root (double root) 2. x 2 + 5 x – 2 = 0 D = 33 2 real, irrational roots 3. 3 x 2 + 8 x + 11 = 0 D = – 68 2 complex roots (complex conjugates) 4. x 2 + 5 x – 24 = 0 D = 121 2 real, rational roots

What is the Quadratic Formula? The quadratic formula can be used to find the

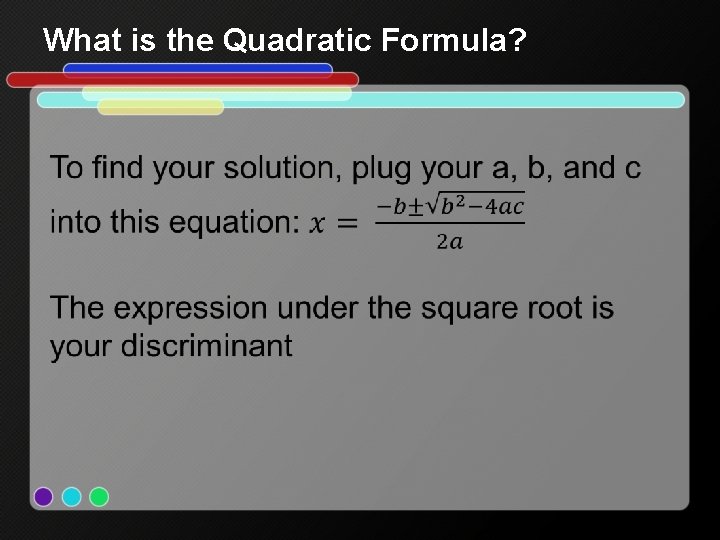
What is the Quadratic Formula? The quadratic formula can be used to find the solutions to any quadratic equation. First you must put the equation in standard form: ax 2+bx+c=0 Then identify you’re a, b, and c.

What is the Quadratic Formula?

What is the Quadratic Formula?

Try These. For each of the following quadratic equations, find the solutions using the

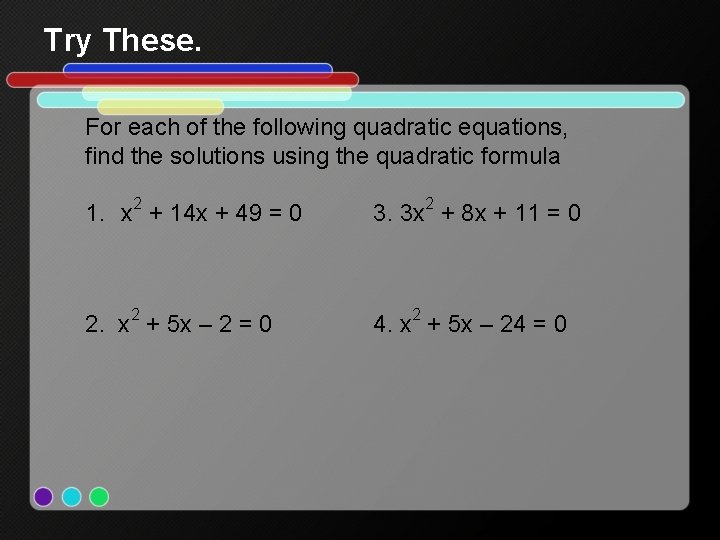
Try These. For each of the following quadratic equations, find the solutions using the quadratic formula 1. x 2 + 14 x + 49 = 0 3. 3 x 2 + 8 x + 11 = 0 2. x 2 + 5 x – 2 = 0 4. x 2 + 5 x – 24 = 0