The Dirac Comb A First Glance at Periodic

The Dirac Comb: A First Glance at Periodic Potential Jed Brody

Outline • Review of basic quantum mechanics • Solution to the Dirac comb problem • Some semiconductor devices I made 2

The Schrödinger Equation • Given V(x) and boundary conditions, find (x) and E that satisfy • We generally find an infinite number of solutions: 1(x) and E 1 2(x) and E 2 All energies except 3(x) and E 3. . . E 1, E 2, E 3, etc. are forbidden!!! 3

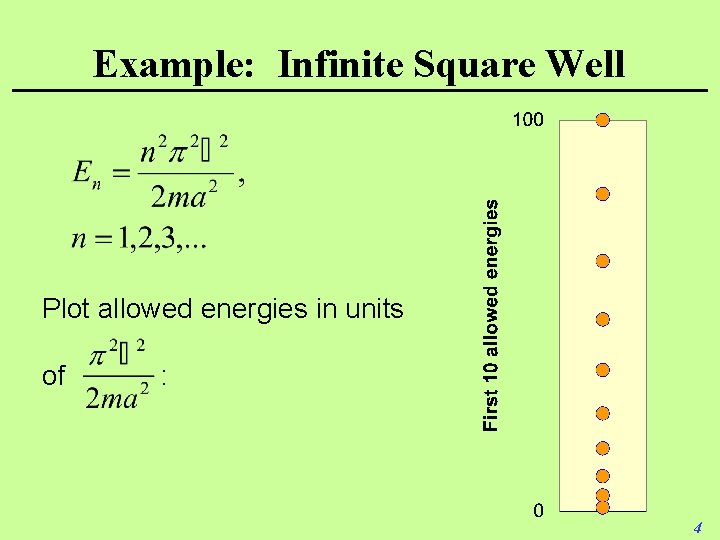
Example: Infinite Square Well Plot allowed energies in units of : 4

Continuity of and d /dx • is continuous everywhere • d /dx is continuous everywhere except where V is infinite • If V(x)=- (x-a), Outline of derivation: • Integrate Schrödinger equation from a-e to a+e • Let e 0 5

Commuting Operators If operators A and B commute ([A, B]=AB-BA=0), then we can find eigenfunctions of A that are also eigenfunctions of B. Proof: Let [A, B] operate on a 1, an eigenfunction of A with eigenvalue a 1 (A a 1 =a 1 a 1): 6

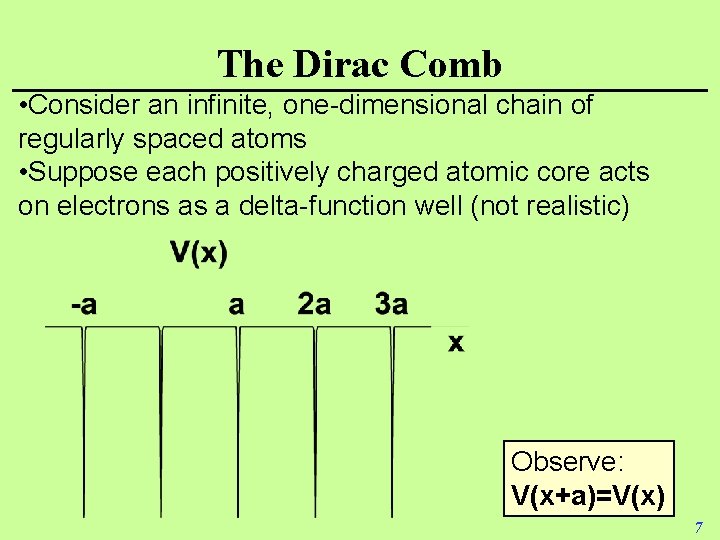
The Dirac Comb • Consider an infinite, one-dimensional chain of regularly spaced atoms • Suppose each positively charged atomic core acts on electrons as a delta-function well (not realistic) Observe: V(x+a)=V(x) 7

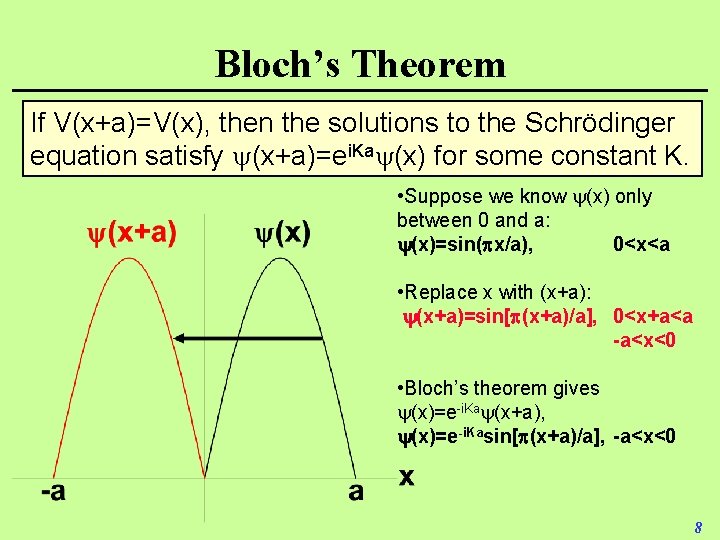
Bloch’s Theorem If V(x+a)=V(x), then the solutions to the Schrödinger equation satisfy (x+a)=ei. Ka (x) for some constant K. • Suppose we know (x) only between 0 and a: (x)=sin( x/a), 0<x<a • Replace x with (x+a): (x+a)=sin[ (x+a)/a], 0<x+a<a -a<x<0 • Bloch’s theorem gives (x)=e-i. Ka (x+a), (x)=e-i. Kasin[ (x+a)/a], -a<x<0 8

First Step of Proof: D and H commute • Define the displacement operator: Df(x)=f(x+a) • H is the Hamiltonian, (-ħ 2/2 m)d 2/dx 2+V(x), for a periodic potential: V(x+a)=V(x) • If D commutes with (-ħ 2/2 m)d 2/dx 2 and with V(x), then D commutes with H • D commutes with (-ħ 2/2 m)d 2/dx 2 because taking the second derivative of a function and then shifting it to the left is the same as shifting it to the left and then taking its second derivative • [D, V(x)]f(x)=[DV(x)-V(x)D]f(x) =DV(x)f(x)-V(x)f(x+a) =V(x+a)f(x+a)-V(x)f(x+a) =0 because V(x+a)=V(x) 9

Completion of Proof • D and H commute, so we can choose eigenfunctions of H that are also eigenfunctions of D • Let D act on one of these eigenfunctions: D (x)= (x), where is the eigenvalue of D • Thus since D (x)= (x+a), (x+a)= (x) • Note that (x+2 a)= 2 (x), (x+3 a)= 3 (x), etc. • To keep (x) from blowing up or vanishing upon repeated applications of D, | |=1 (x+a)=ei. Ka (x) 10

Restrictions on K • The electrical properties of a solid deep in its bulk are independent of edge effects. To avoid edge effects, use periodic boundary conditions • Wrap the x axis around on itself, forming a loop of length Na; N is the very large number of potential wells • After travelling a distance Na, you return to your starting point: (x+Na)= (x) • Bloch’s theorem gives (x+Na)=ei. NKa (x), so ei. NKa=1 NKa=2 n K=2 n/(Na), n=0, ± 1, ± 2, . . . 11

Solving the Dirac Comb Problem The potential is a series of delta functions: In between delta functions (e. g. , 0<x<a), V(x)=0: 12

Conditions on (x) at x=0 Replace x with (x+a): Apply Bloch’s theorem, (x)=e-i. Ka (x+a): (x) must be continuous at x=0: 13

Equation To Find Allowed Energies • Eliminating A and B from previous equations gives • On LHS, we know K=2 n/(Na), where n=0, ± 1, ± 2, … • On RHS, define z ka=a(2 m. E)1/2/ħ and m a/ħ 2 Example: N=8 n 2 n/N cos(2 n/N) 0 0 1 ± /4 21/2/2 ± /2 0 ± 3 ± 4 ± 3 /4 ± -21/2/2 -1 ± 5 ± 6 ± 5 /4 ± 3 /2 -21/2/2 0 14

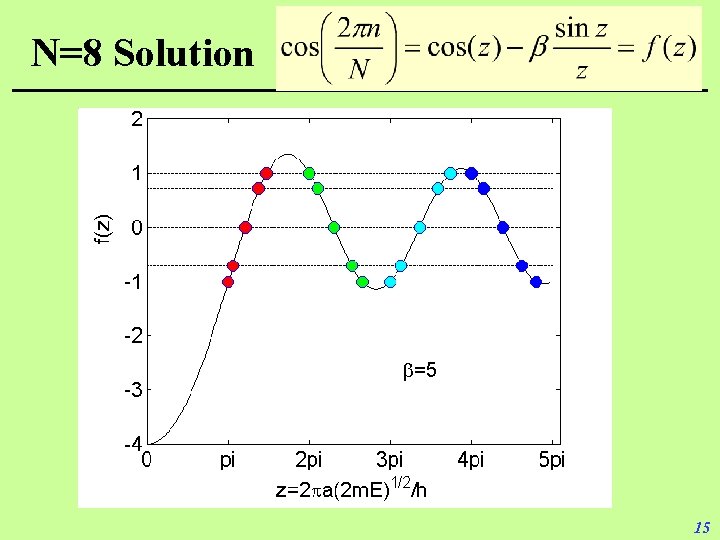
N=8 Solution =5 15

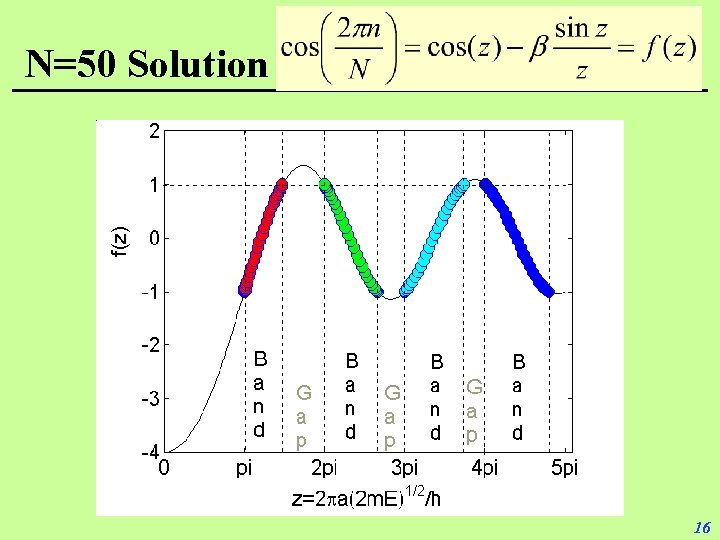
N=50 Solution 16