The different types of order What is order

The different types of order

What is order? « Disposition organisée, structurée selon certains principes, chaque élément ayant la place qui lui convient » Larousse ‘’The arrangement or disposition of people or things in relation to each other according to a particular sequence, pattern, or method’’ Oxford dictionnary Order ‘’An infinite set of points is geometrically ordered, if it is generated by a determinist algorithm of finite complexity’’ D. Gratias et al. , Annu. Rev. Mat. Res. (2003)

Correlation functions Time-dependant pair correlation function Temporal, statistical, volume means O Density-density correlation function:

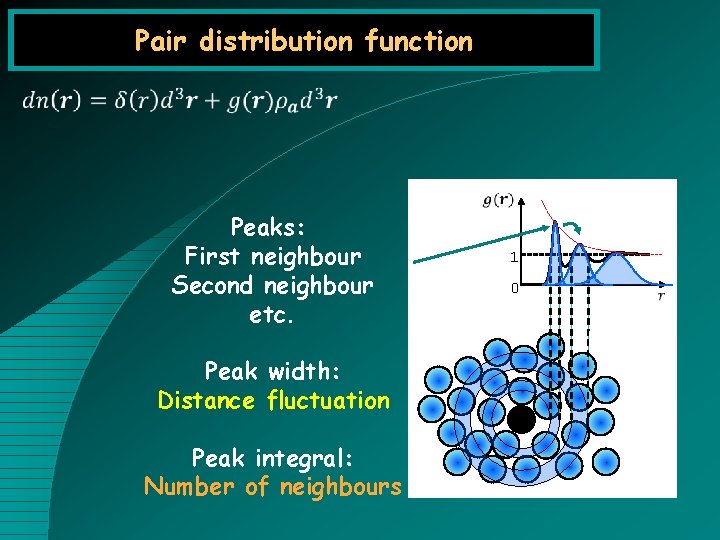
Pair distribution function Peaks: First neighbour Second neighbour etc. Peak width: Distance fluctuation Peak integral: Number of neighbours 1 0

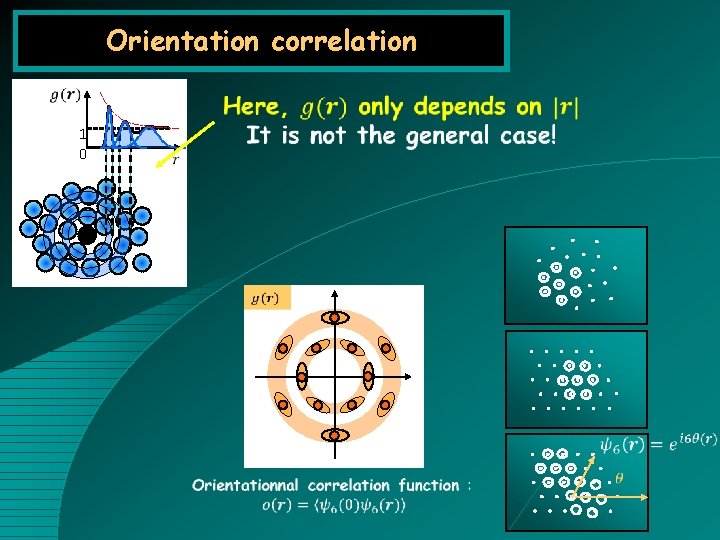
Orientation correlation 1 0

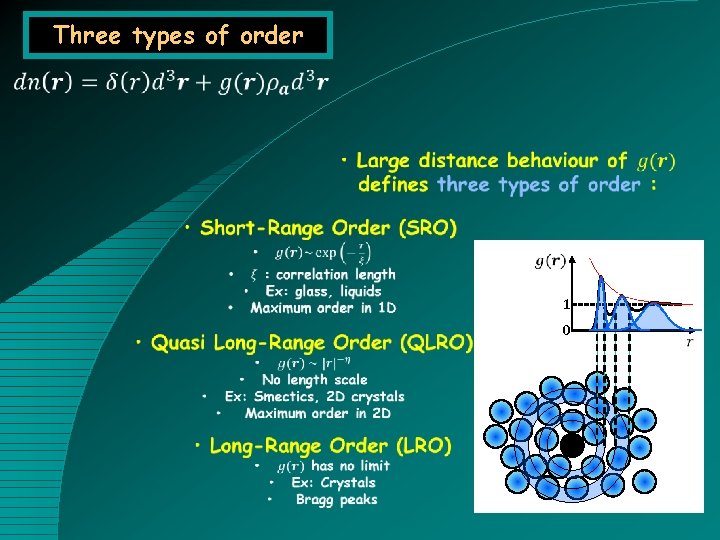
Three types of order 1 0

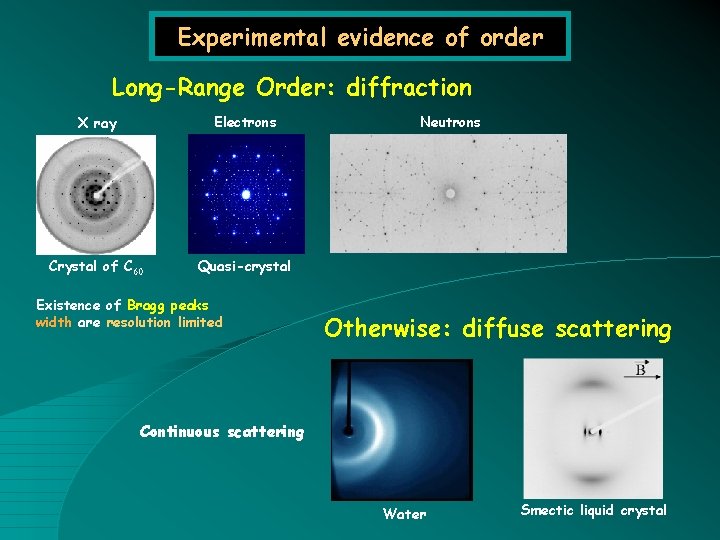
Experimental evidence of order Long-Range Order: diffraction X ray Electrons Crystal of C 60 Quasi-crystal Existence of Bragg peaks width are resolution limited Neutrons Otherwise: diffuse scattering Continuous scattering Water Smectic liquid crystal

Short-Range Order (SRO) • Order in 1 D • Liquids, amorphous, glass • Amorphous state (disordered, non-crystalline) • Amorphous recrystallize when heated. Metals, silicon, water. • Glass becomes liquid through a vitreous transition. Silicon, Sulfur, Glycerol, Se (+As), obsidian, diatoms • Liquid : same pdf, but dynamics.

Melting and Quasi Long-Range Order Melting in 3 D 1 er order Phase transition LRO Solid Liquid

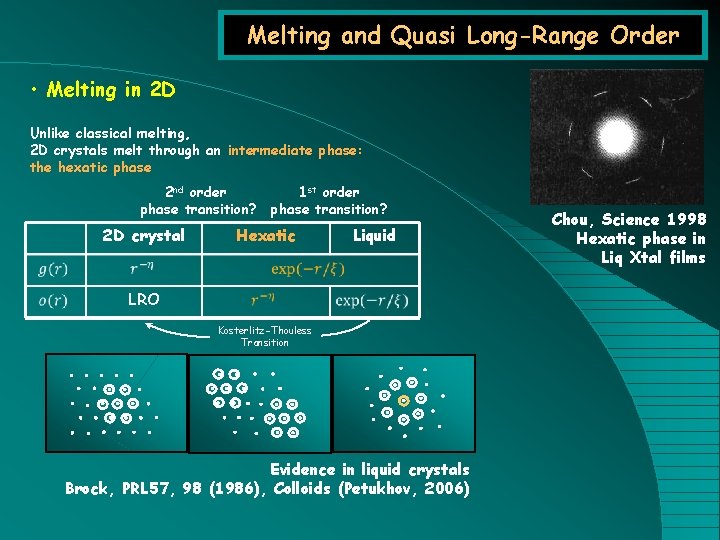
Melting and Quasi Long-Range Order • Melting in 2 D Unlike classical melting, 2 D crystals melt through an intermediate phase: the hexatic phase 2 nd order phase transition? 2 D crystal 1 st order phase transition? Hexatic Liquid LRO Kosterlitz-Thouless Transition Evidence in liquid crystals Brock, PRL 57, 98 (1986), Colloids (Petukhov, 2006) Chou, Science 1998 Hexatic phase in Liq Xtal films

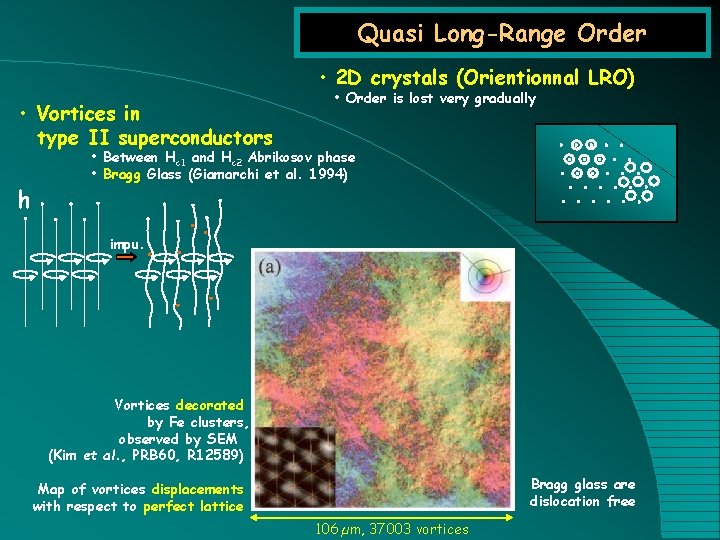
Quasi Long-Range Order • 2 D crystals (Orientionnal LRO) • Vortices in type II superconductors h • Order is lost very gradually • Between Hc 1 and Hc 2 Abrikosov phase • Bragg Glass (Giamarchi et al. 1994) impu. Vortices decorated by Fe clusters, observed by SEM (Kim et al. , PRB 60, R 12589) Bragg glass are dislocation free Map of vortices displacements with respect to perfect lattice 106 µm, 37003 vortices

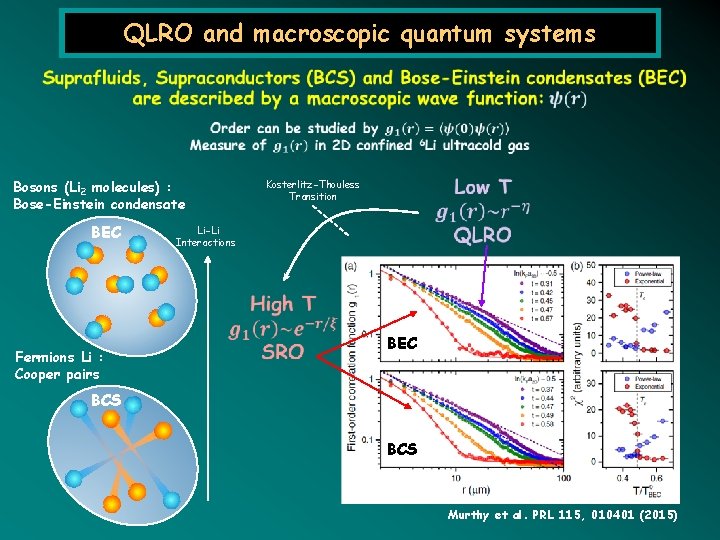
QLRO and macroscopic quantum systems Bosons (Li 2 molecules) : Bose-Einstein condensate BEC Kosterlitz-Thouless Transition Li-Li Interactions Fermions Li : Cooper pairs BEC BCS Murthy et al. PRL 115, 010401 (2015)

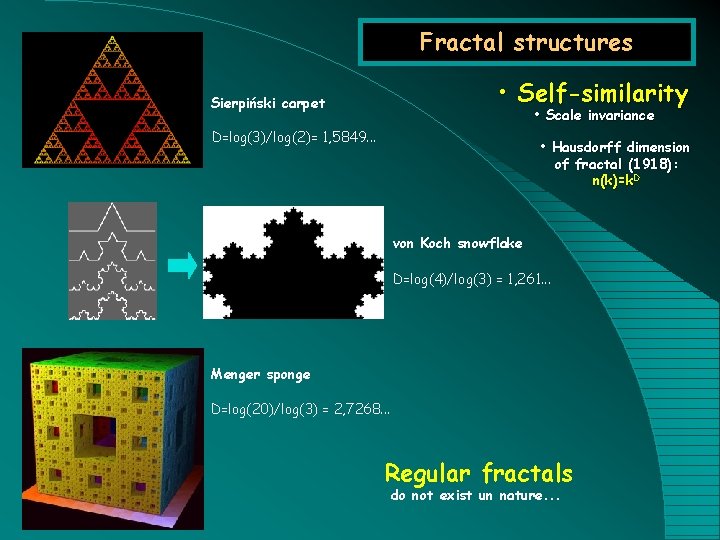
Fractal structures • Self-similarity Sierpiński carpet • Scale invariance D=log(3)/log(2)= 1, 5849. . . • Hausdorff dimension of fractal (1918): n(k)=k. D von Koch snowflake D=log(4)/log(3) = 1, 261. . . Menger sponge D=log(20)/log(3) = 2, 7268. . . Regular fractals do not exist un nature. . .

Irregular fractals Lichtenberg figures

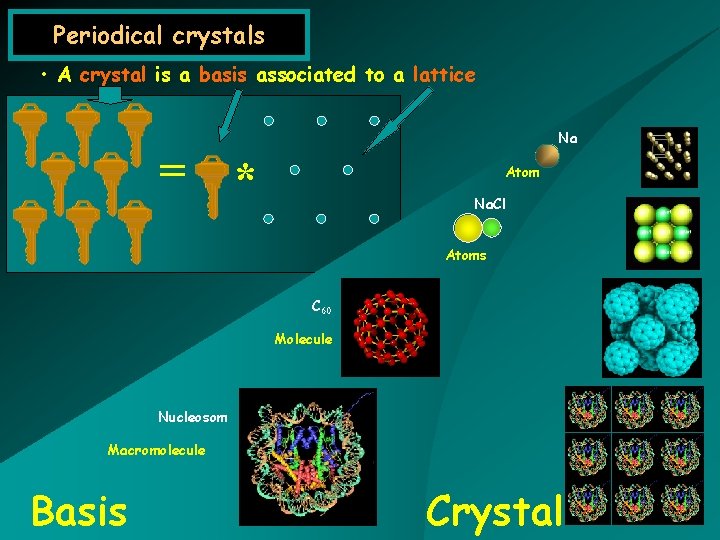
Periodical crystals • A crystal is a basis associated to a lattice Na = * Atom Na. Cl Atoms C 60 Molecule Nucleosom Macromolecule Basis Crystal

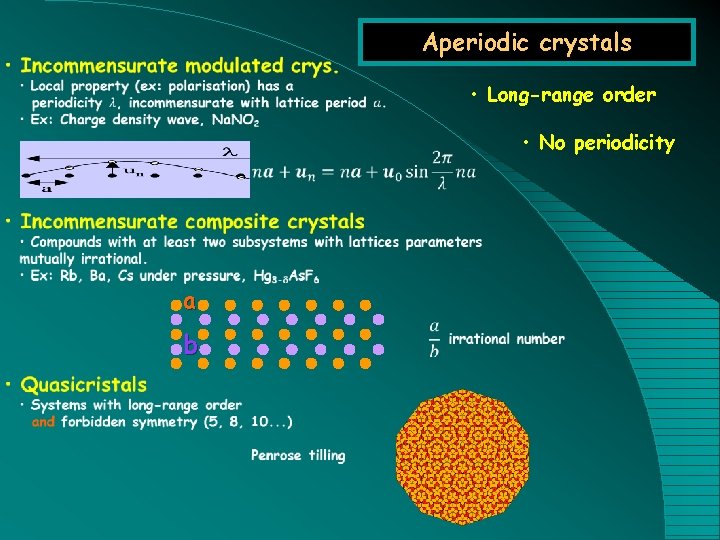
Aperiodic crystals • Long-range order • No periodicity a b

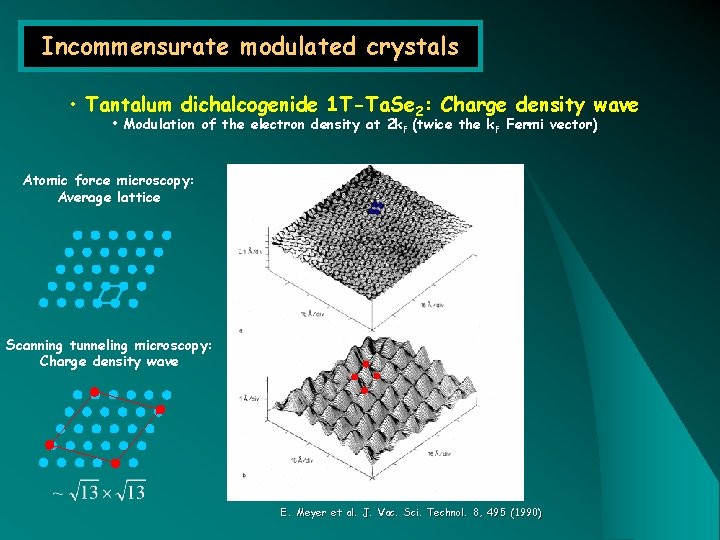
Incommensurate modulated crystals • Tantalum dichalcogenide 1 T-Ta. Se 2: Charge density wave • Modulation of the electron density at 2 k. F (twice the k. F Fermi vector) Atomic force microscopy: Average lattice Scanning tunneling microscopy: Charge density wave E. Meyer et al. J. Vac. Sci. Technol. 8, 495 (1990)

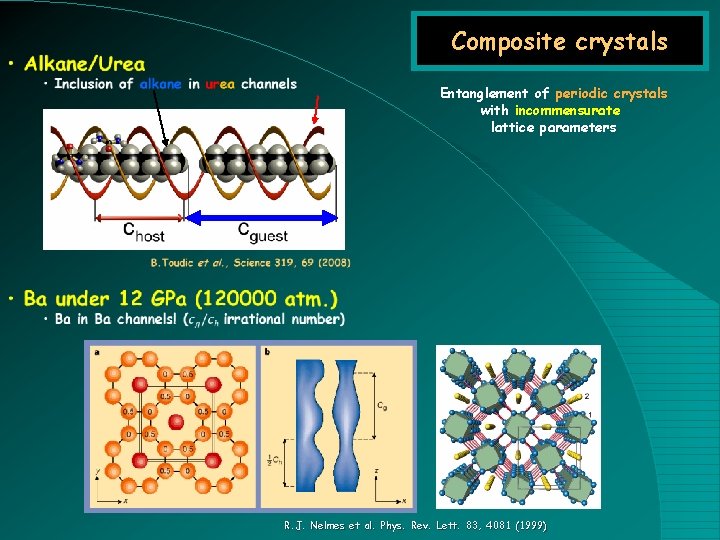
Composite crystals Entanglement of periodic crystals with incommensurate lattice parameters R. J. Nelmes et al. Phys. Rev. Lett. 83, 4081 (1999)

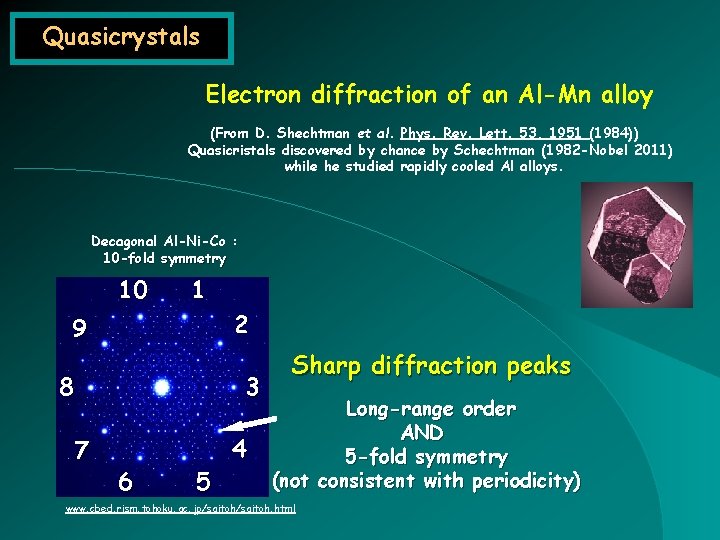
Quasicrystals Electron diffraction of an Al-Mn alloy (From D. Shechtman et al. Phys. Rev. Lett. 53, 1951 (1984)) Quasicristals discovered by chance by Schechtman (1982 -Nobel 2011) while he studied rapidly cooled Al alloys. Decagonal Al-Ni-Co : 10 -fold symmetry 10 1 2 9 8 7 3 6 5 4 Sharp diffraction peaks Long-range order AND 5 -fold symmetry (not consistent with periodicity) www. cbed. rism. tohoku. ac. jp/saitoh. html

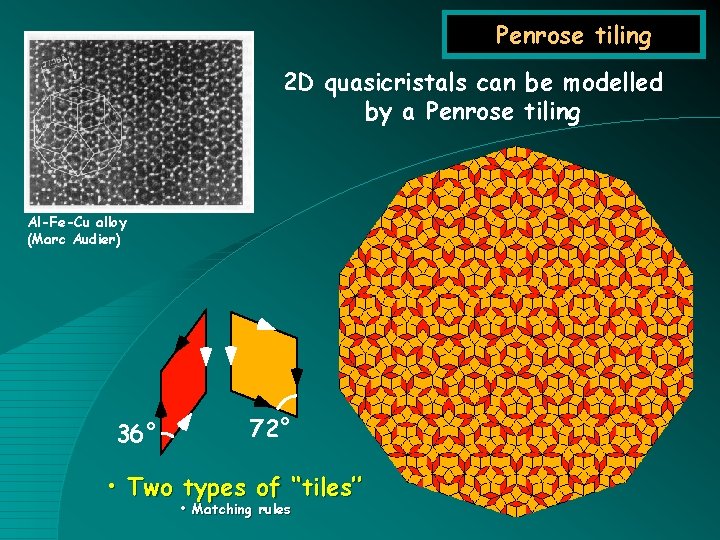
Penrose tiling 2 D quasicristals can be modelled by a Penrose tiling Al-Fe-Cu alloy (Marc Audier) 36° 72° • Two types of ‘‘tiles’’ • Matching rules

Penrose tiling • Quasiperiodic tilings before Penrose… Darb-i Imam temple Isfahan, Iran XVe • Non periodic tilings • Long-range order WITHOUT periodicity • N-fold symmetry for any N 12 -fold symmety

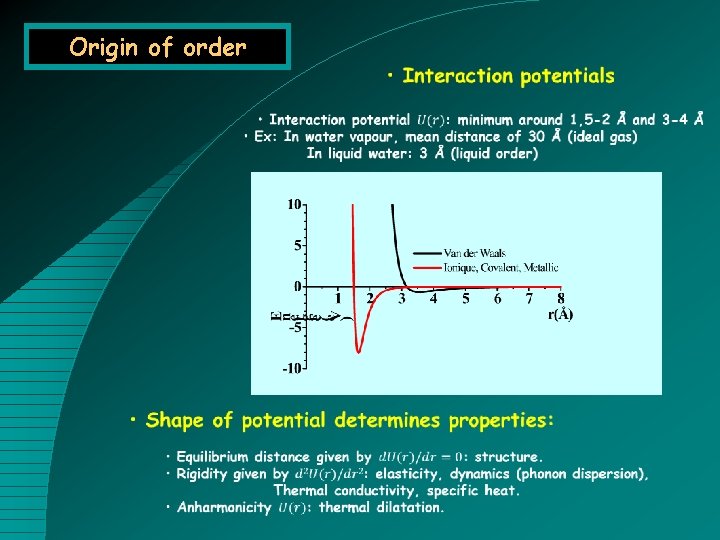
Origin of order

Five types of bondings • Ionic bonding (heteropolar) • Coulombic interaction between ions. • Strong bonding (e. V), nonsaturable and nondirectional. • Ex: Na. Cl, Li. F • Covalent bond (homopolar) • Electrons shared by two atoms. • Strong bonding (1. 5 e. V O-O, 3. 6 e. V C-C ), saturable and directional. • Ex: Diamond • Metallic bonding • Delocalized electrons. • Intermediate bonding (0. 5 e. V Cu), nonsaturable and nondirectional. • Ex: All metals (Na, Cu, U), organic conductors. • van der Waals bonding • Dipole (induced) – dipole interaction. • Weak bonding (10 me. V), nonsaturable and nondirectional. • Ex: Noble gas (Ar, Xe), molecular crystals. • Hydrogen bond • Ionic bonding between H and electronegative atom. • Weak bonding (100 me. V) directional. • Ex: Ice (O-H---O 0. 26 e. V), organic and biologic crystals. 300 K (k. BT) 25. 8 me. V 6. 25 THz 208. 5 cm-1 48 µm

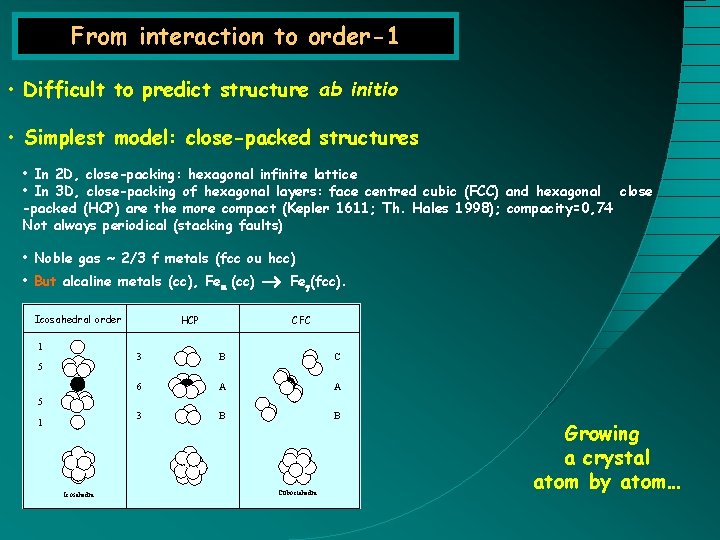
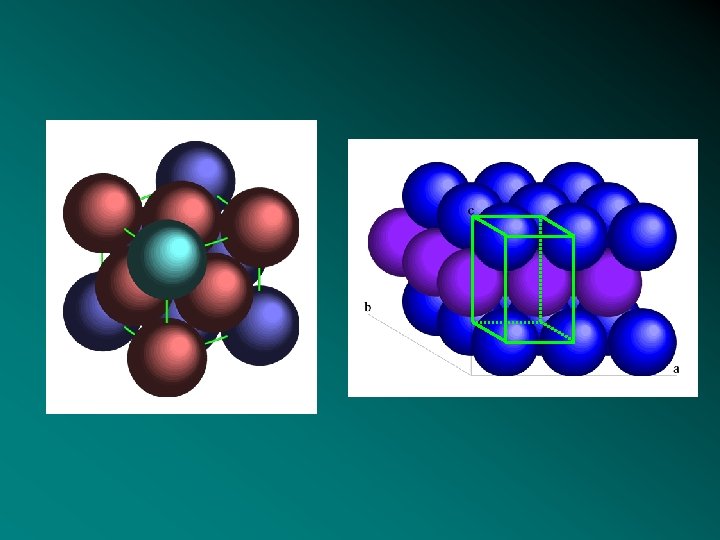
From interaction to order-1 • Difficult to predict structure ab initio • Simplest model: close-packed structures • In 2 D, close-packing: hexagonal infinite lattice • In 3 D, close-packing of hexagonal layers: face centred cubic (FCC) and hexagonal close -packed (HCP) are the more compact (Kepler 1611; Th. Hales 1998); compacity=0, 74 Not always periodical (stacking faults) • Noble gas ~ 2/3 f metals (fcc ou hcc) • But alcaline metals (cc), Fea (cc) Icosahedral order 1 5 HCP Feg(fcc). CFC 3 B C 6 A A 3 B B 5 1 Icosahedra Cuboctahedra Growing a crystal atom by atom…

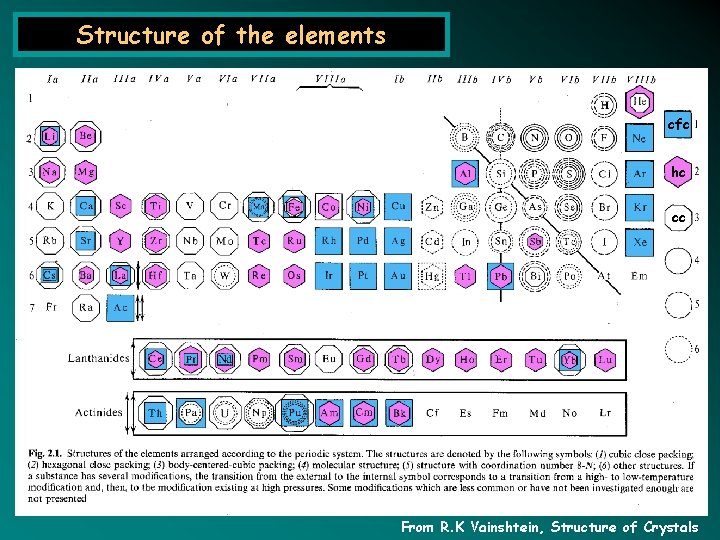
Structure of the elements cfc hc cc From R. K Vainshtein, Structure of Crystals

From interactions to order-2 • 3 D close-packing of 4 atoms: tetrahedra • Impossible to fill Euclidian space by perfect tetrahedra (dihedral angle = 70, 528°) But LOCALLY, tiling of distorded tetrahedra is possible Icosahedrea 7. 36° • Impossible to fill Euclidian space with distorted tetrahedra, so that a constant number of tetrahedra sharing a common edge Topological frustration Interactions favor icosahedral local order not consistent with infinite system. Frustration produces defects (liquids, glass)

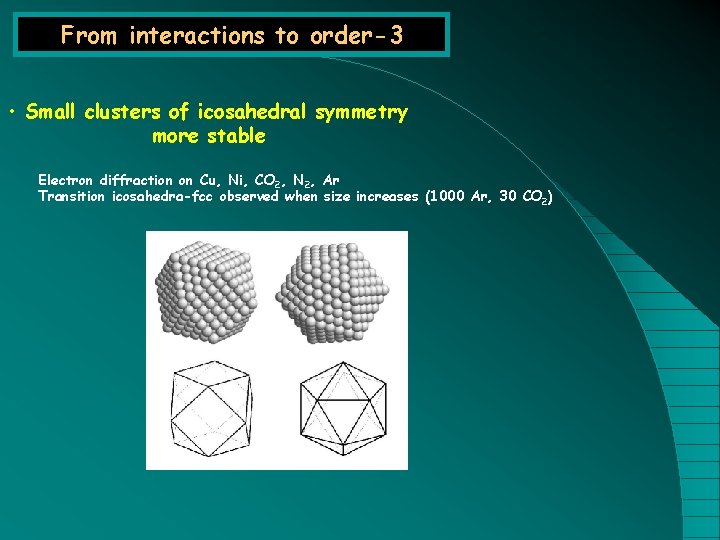
From interactions to order-3 • Small clusters of icosahedral symmetry more stable Electron diffraction on Cu, Ni, CO 2, N 2, Ar Transition icosahedra-fcc observed when size increases (1000 Ar, 30 CO 2)

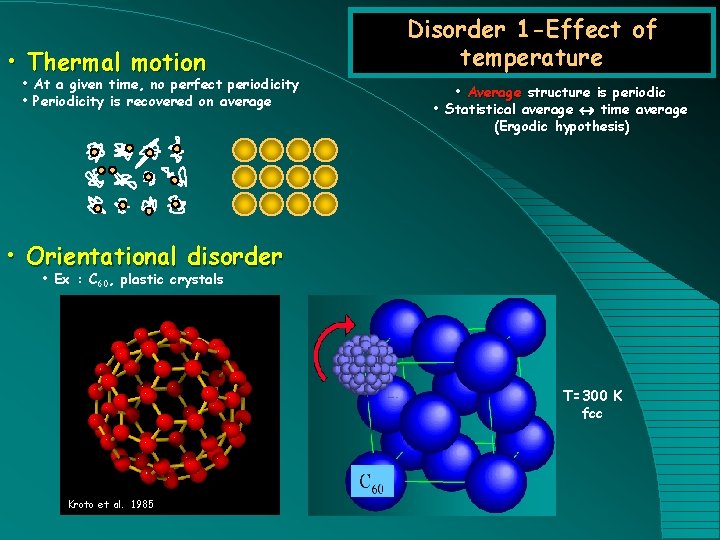
• Thermal motion • At a given time, no perfect periodicity • Periodicity is recovered on average Disorder 1 -Effect of temperature • Average structure is periodic • Statistical average time average (Ergodic hypothesis) • Orientational disorder • Ex : C 60, plastic crystals T=300 K fcc Kroto et al. 1985

Real crystals: 2 -Defects www. techfak. uni-kiel. de/matwis/amat/def_en/makeindex. html • Topological defects • Dimension 0 • Vacancies, intersticials • Deformations which change the local atomic environment, such as the number of neighbors Vacancy • Always present (2. 10 -4 Cu at 300 K) • Diffusion, colored centers Intersticial • Plasticity (Impurety) • semi-cond. doping • Colors of jewels • Plasticity • Dimension 1 • Dislocations (metal plasticity) • Disclinations (2 D, liquid crystals) Dislocation Disclination • Dimension 2 • Surfaces, stacking faults • Grain boundaries, twins Surface Stacking faults Grain boundary

Dislocation creep • GP zone (Guinier-Preston) • Clusters of atom • Hardening of Al alloys (Concorde) • Platelets in Al-1. 7 at. %Cu From M. Karlík et B. Jouffrey, J. Phys. III France, 6 (1996) 825 • GP shear by an edge dislocation • High resolution electron microscopy

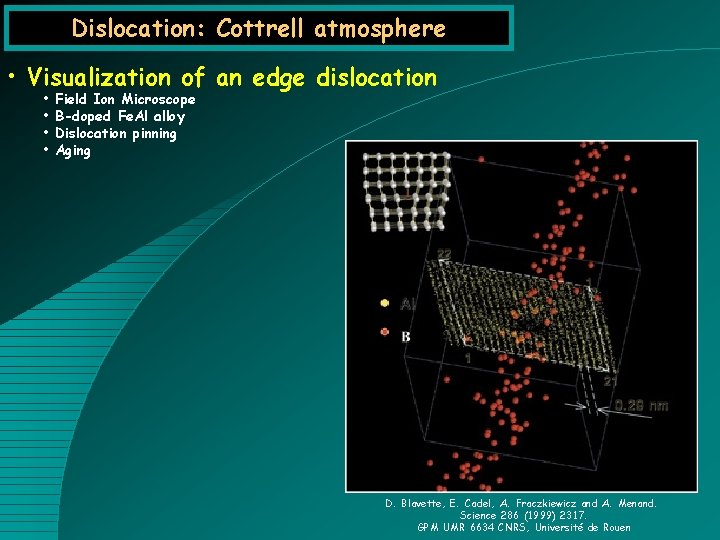
Dislocation: Cottrell atmosphere • Visualization of an edge dislocation • • Field Ion Microscope B-doped Fe. Al alloy Dislocation pinning Aging D. Blavette, E. Cadel, A. Fraczkiewicz and A. Menand. Science 286 (1999) 2317. GPM UMR 6634 CNRS, Université de Rouen

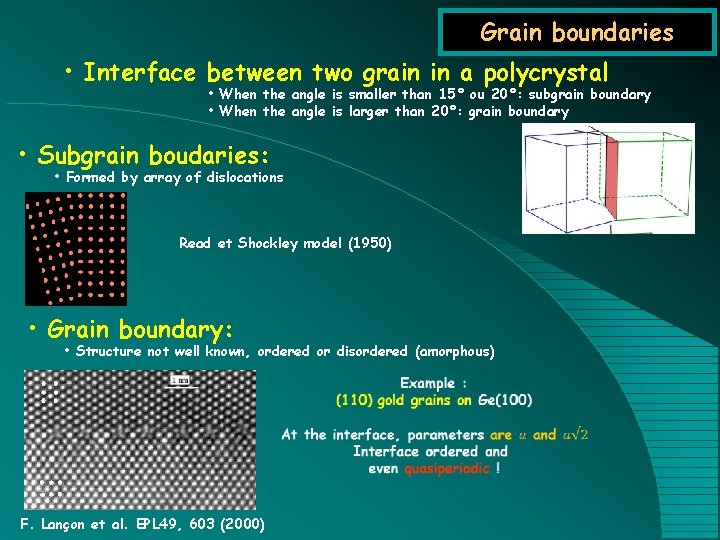
Grain boundaries • Interface between two grain in a polycrystal • When the angle is smaller than 15° ou 20°: subgrain boundary • When the angle is larger than 20°: grain boundary • Subgrain boudaries: • Formed by array of dislocations Read et Shockley model (1950) • Grain boundary: • Structure not well known, ordered or disordered (amorphous) F. Lançon et al. EPL 49, 603 (2000)

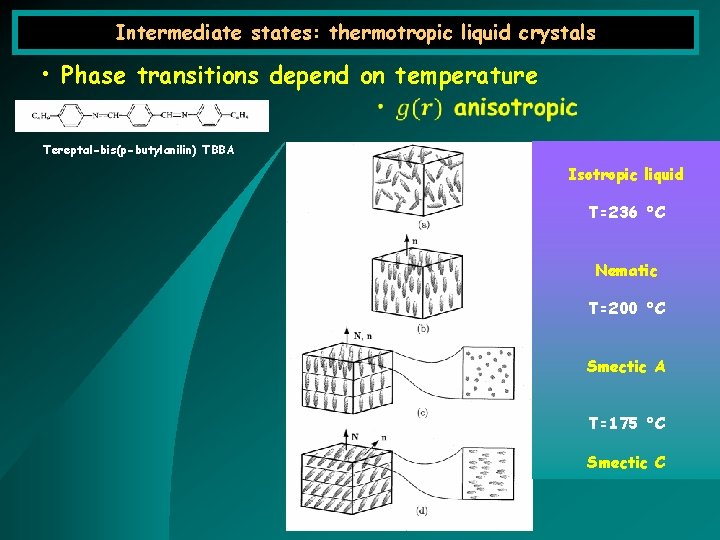
Intermediate states: thermotropic liquid crystals • Phase transitions depend on temperature Tereptal-bis(p-butylanilin) TBBA Isotropic liquid T=236 °C Nematic T=200 °C Smectic A T=175 °C Smectic C

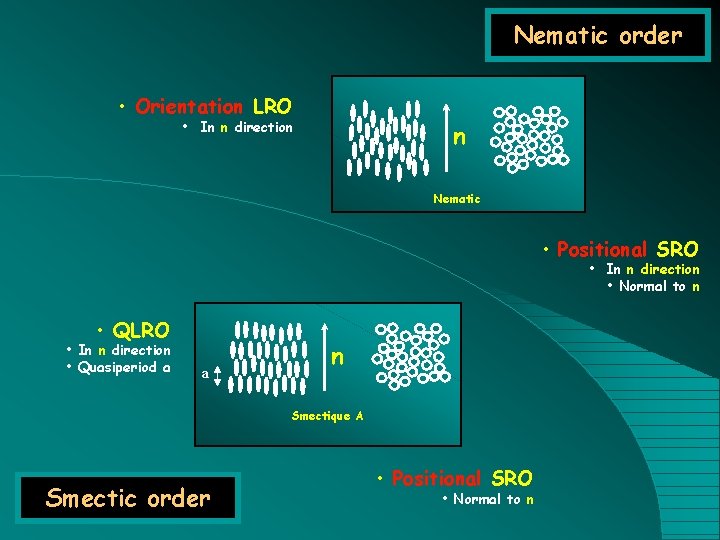
Nematic order • Orientation LRO • In n direction n Nematic • Positional SRO • In n direction • Normal to n • QLRO • In n direction • Quasiperiod a a n Smectique A Smectic order • Positional SRO • Normal to n

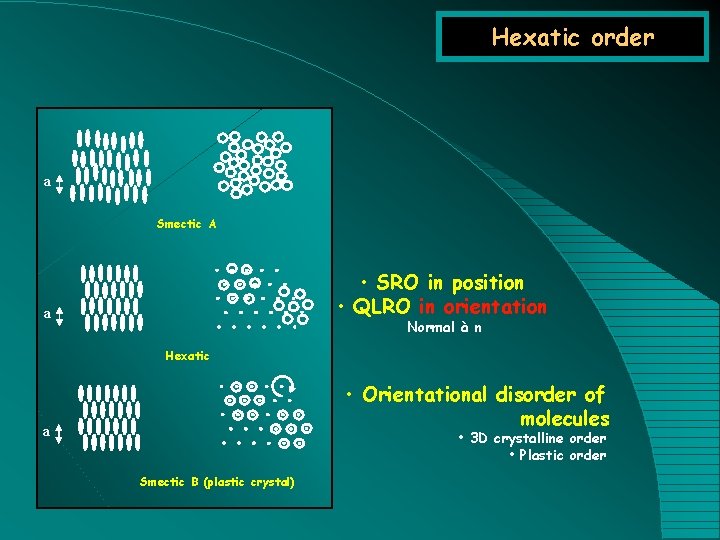
Hexatic order a Smectic A • SRO in position • QLRO in orientation a Normal à n Hexatic • Orientational disorder of molecules a • 3 D crystalline order • Plastic order Smectic B (plastic crystal)

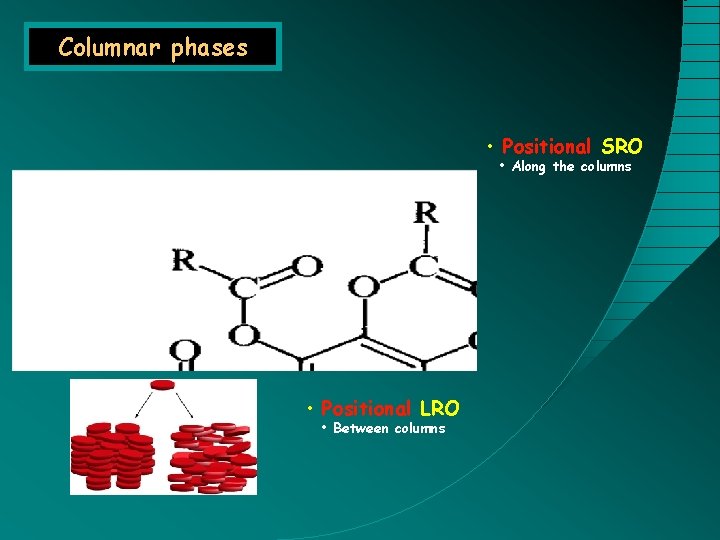
Columnar phases • Positional SRO • Along the columns Discotic molecules • Positional LRO • Between columns

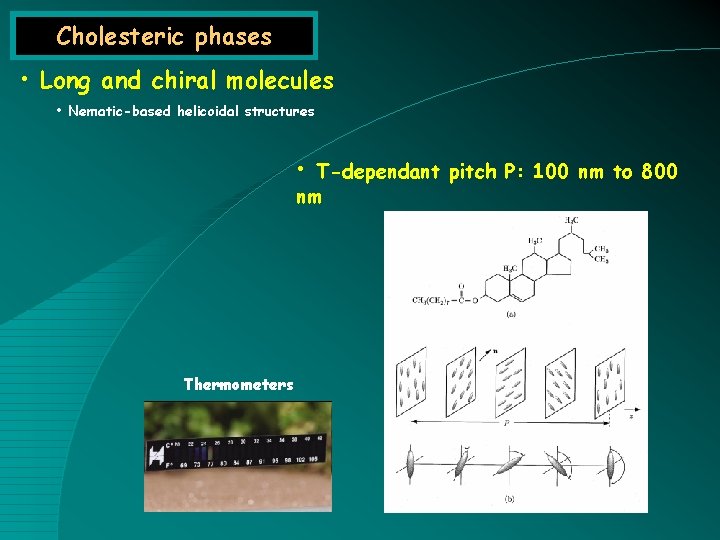
Cholesteric phases • Long and chiral molecules • Nematic-based helicoidal structures • T-dependant pitch P: 100 nm to 800 nm Thermometers

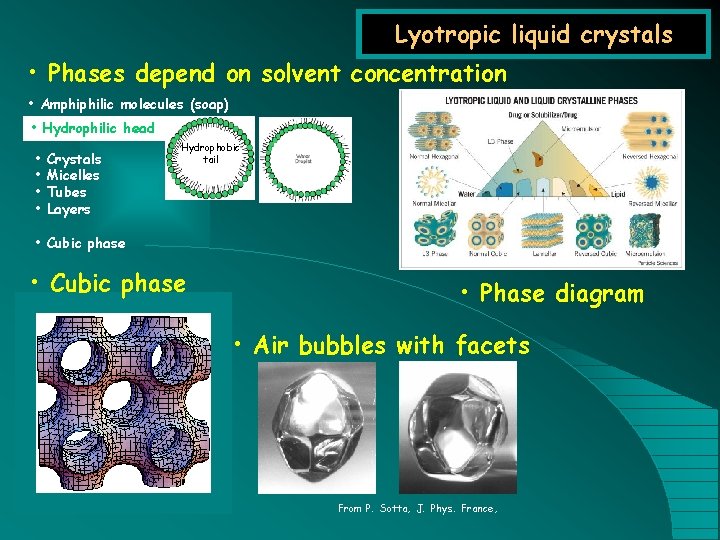
Lyotropic liquid crystals • Phases depend on solvent concentration • Amphiphilic molecules (soap) • Hydrophilic head • • Crystals Micelles Tubes Layers Hydrophobic tail • Cubic phase • Phase diagram • Air bubbles with facets From P. Sotta, J. Phys. France,

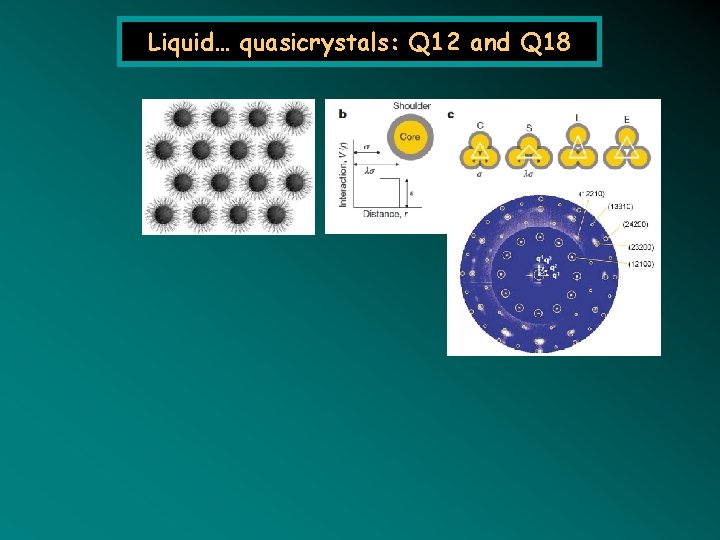
Liquid… quasicrystals: Q 12 and Q 18 Dotera 2014