The diagram shows a rectangular box 25 cm

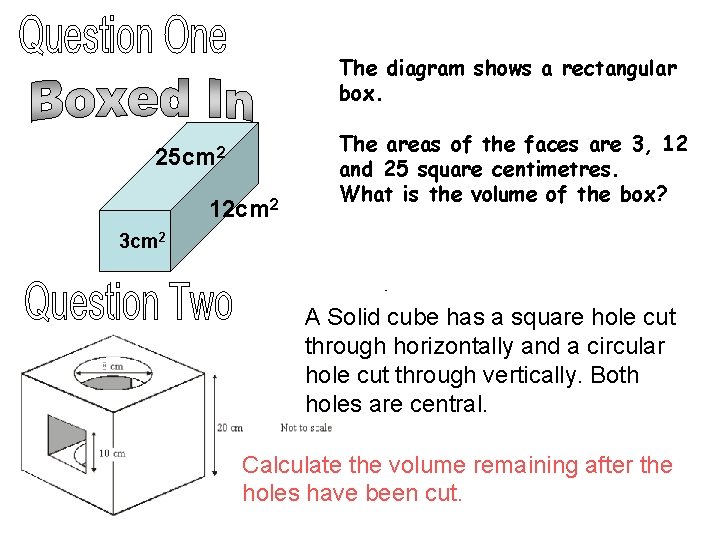
The diagram shows a rectangular box. 25 cm 2 12 cm 2 The areas of the faces are 3, 12 and 25 square centimetres. What is the volume of the box? 3 cm 2 A Solid cube has a square hole cut through horizontally and a circular hole cut through vertically. Both holes are central. Calculate the volume remaining after the holes have been cut.

Answers • Question One • l = 2. 5 cm, w = 1. 2 cm, h = 10 cm, volume = 30 cm 3 • Question Two Volume cube = 203 = 8000 cm 3 Square hole = 102 × 20 = 2000 cm 3 Circular holes = 2 (pie × 42 × 5) = 502. 7 cm 3 Volume left = 5497. 35 cm 3

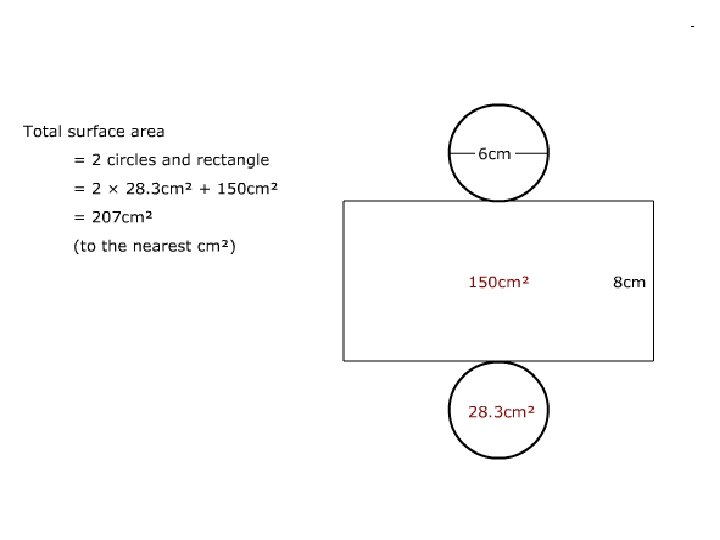
Task • Using the piece of card • Make a net of a cylinder • Make sure it is accurate so it fits together perfectly • Do not worry about making tabs • Once you have done this • Find the total surface area

Volume of a cylinder A cylinder is a special type of prism with a circular crosssection. Remember, the volume of a prism can be found by multiplying the area of the cross-section by the height of the prism. r The volume of a cylinder is given by: Volume = area of circular base × height h or V = πr 2 h

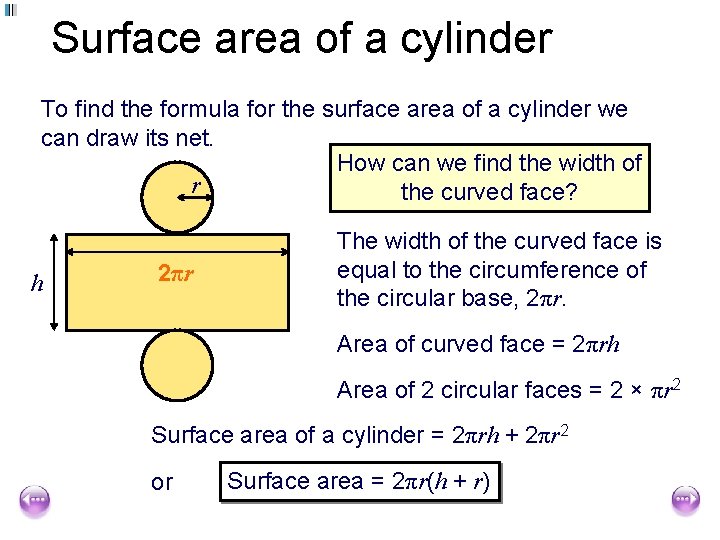
Surface area of a cylinder To find the formula for the surface area of a cylinder we can draw its net. How can we find the width of r the curved face? h ? 2πr The width of the curved face is equal to the circumference of the circular base, 2πr. Area of curved face = 2πrh Area of 2 circular faces = 2 × πr 2 Surface area of a cylinder = 2πrh + 2πr 2 or Surface area = 2πr(h + r)

Lesson Objective

Plenary