The Design of Application Specific Integrated Circuits with

The Design of Application Specific Integrated Circuits with High Level Synthesis Approaches Shiann-Rong Kuang (鄺獻榮) Assistant Professor Dept. of Computer Science and Engineering National Sun Yat-Sen University NSYSU CSE 2002/9 1

Outlines Introduction Novel High Level Synthesis Approaches Integrated Data Path Synthesis Approach Pipelined Control Path Synthesis Approach Dynamic Pipelining Approach ASICs design Binary Arithmetic Coder – Low-Error Fixed-Width Multipliers Fuzzy Color Corrector Future Work NSYSU CSE 2002/9 2

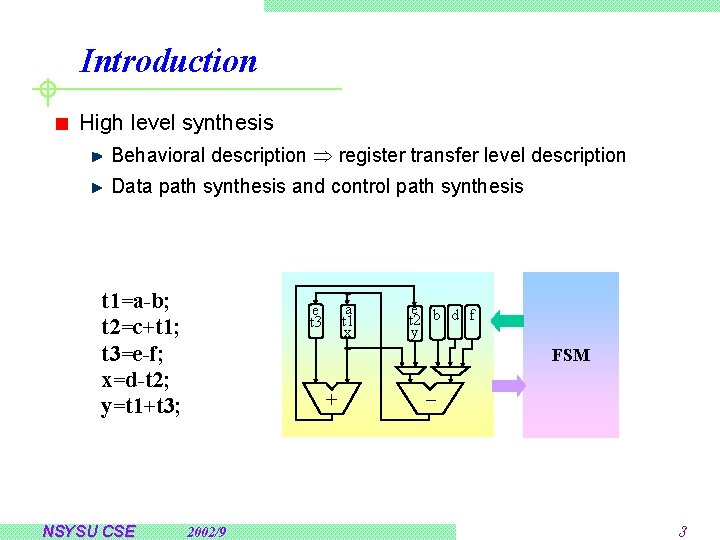
Introduction High level synthesis Behavioral description register transfer level description Data path synthesis and control path synthesis t 1=a-b; t 2=c+t 1; t 3=e-f; x=d-t 2; y=t 1+t 3; NSYSU CSE a t 1 x e t 3 e t 2 b d f y FSM + 2002/9 _ 3

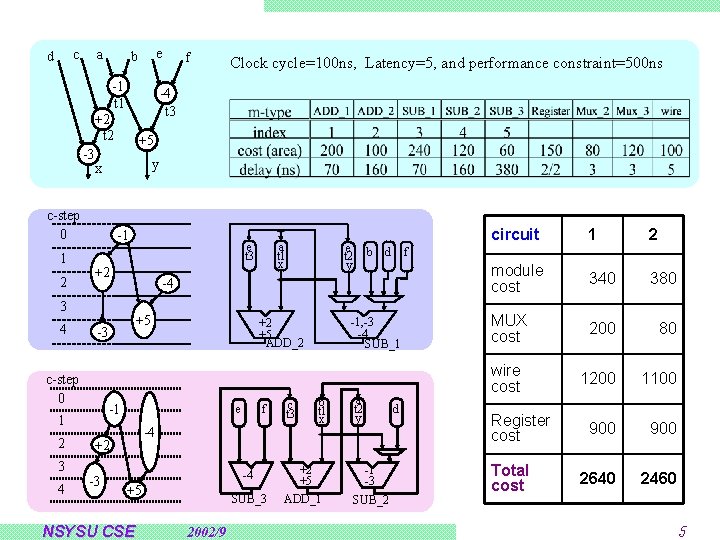
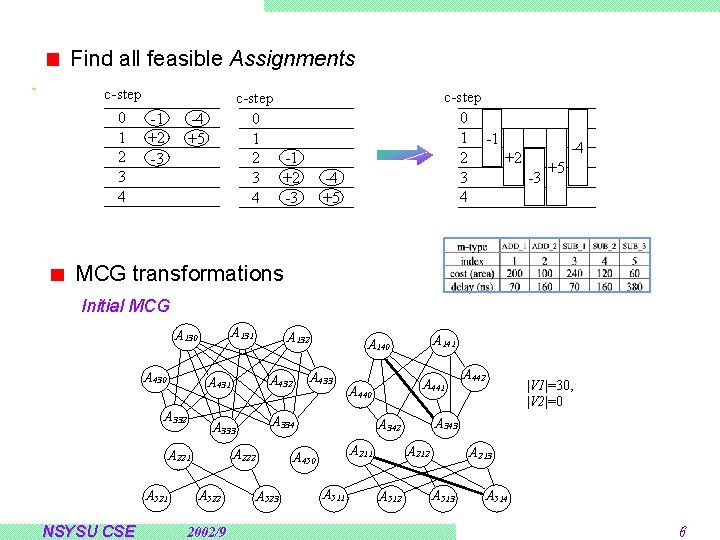
Integrated Data Path Synthesis Approach Data Path Synthesis module selection, scheduling, and allocation: highly interdependent separately solve them the best designs may not be explored Proposed Data Path Synthesis Approach combine module selection, scheduling, and allocation general module selection model – module types with different attributes (delay, area, …) a mixed-vertex compatibility graph model – solve it globally using partial clique partitioning NSYSU CSE 2002/9 4

a c d e b -1 t 1 2 +5 y x c-step 0 1 -1 3 4 +5 e f -4 +2 -3 e t 2 y b d -4 +5 NSYSU CSE SUB_3 2002/9 c t 3 b t 1 x +2 +5 ADD_1 a t 2 y d -1 -3 SUB_2 circuit 1 2 module cost 340 380 MUX cost 200 80 wire cost 1200 1100 900 2640 2460 f -1, -3 -4 SUB_1 +2 +5 ADD_2 -1 1 a t 1 x -4 -3 c-step 0 2 e t 3 +2 3 4 Clock cycle=100 ns, Latency=5, and performance constraint=500 ns -4 t 3 +2 t 2 -3 f Register cost Total cost 5

Find all feasible Assignments c-step 0 -1 1 +2 2 -3 3 4 c-step 0 1 -1 2 3 +2 4 -3 -4 +5 c-step 0 1 -1 -4 2 +2 +5 3 -3 4 -4 +5 MCG transformations Initial MCG A 131 A 130 A 430 A 333 A 521 NSYSU CSE A 522 2002/9 A 211 A 511 A 212 A 512 A 442 |V 1|=30, |V 2|=0 A 343 A 342 A 450 A 523 A 441 A 440 A 334 A 222 A 221 A 140 A 433 A 432 A 431 A 332 A 132 A 213 A 514 6

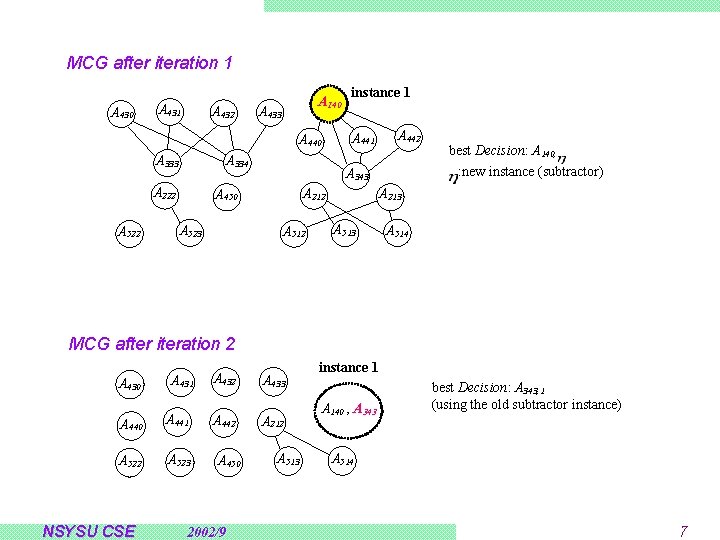
MCG after iteration 1 A 430 A 431 A 432 A 140 A 433 A 440 A 333 A 334 A 222 A 522 A 441 A 442 A 343 A 212 A 450 A 523 instance 1 A 512 best Decision: A 140, : new instance (subtractor) A 213 A 514 MCG after iteration 2 A 430 A 431 A 440 A 441 A 522 A 523 NSYSU CSE A 432 A 433 A 442 A 212 A 450 2002/9 A 513 instance 1 A 140 , A 343 best Decision: A 343, 1 (using the old subtractor instance) A 514 7

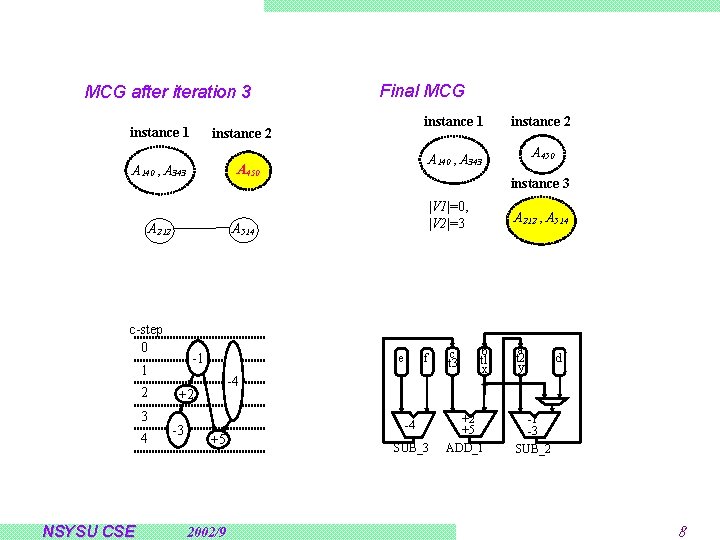
MCG after iteration 3 instance 1 instance 2 A 450 A 140 , A 343 c-step 0 -1 1 3 4 NSYSU CSE instance 1 instance 2 A 140 , A 343 A 450 instance 3 |V 1|=0, |V 2|=3 A 514 A 212 2 Final MCG e -4 +2 -3 f -4 +5 2002/9 SUB_3 c t 3 A 212 , A 514 b t 1 x +2 +5 ADD_1 a t 2 y d -1 -3 SUB_2 8

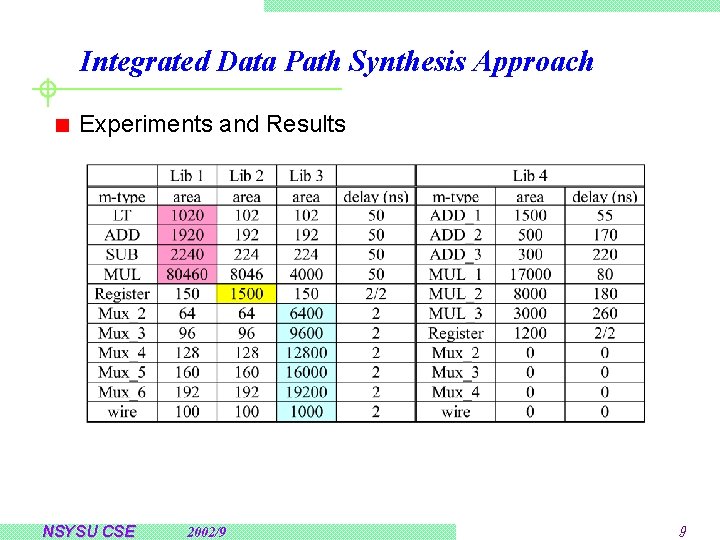
Integrated Data Path Synthesis Approach Experiments and Results NSYSU CSE 2002/9 9

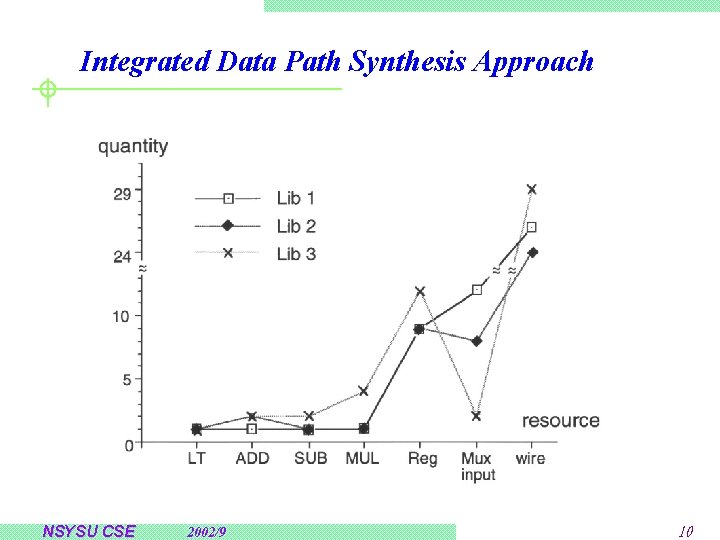
Integrated Data Path Synthesis Approach NSYSU CSE 2002/9 10

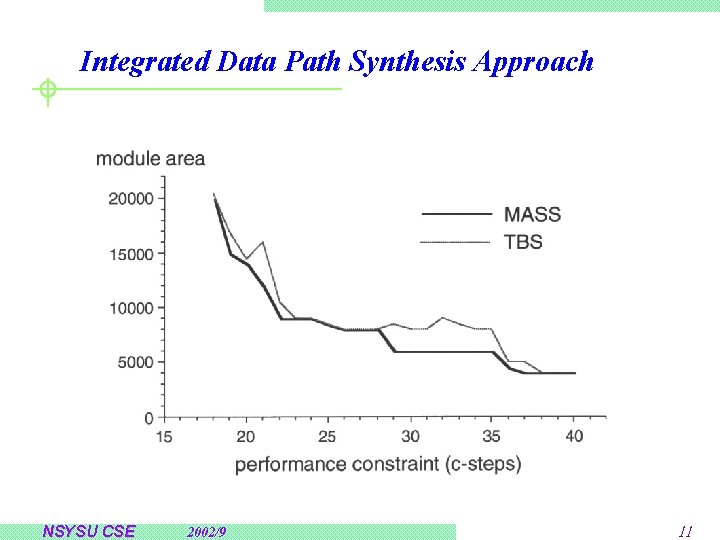
Integrated Data Path Synthesis Approach NSYSU CSE 2002/9 11

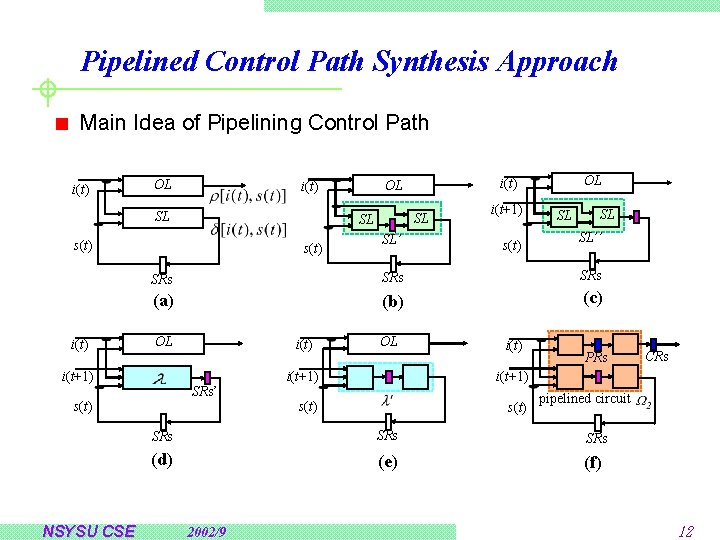
Pipelined Control Path Synthesis Approach Main Idea of Pipelining Control Path i(t) OL SL s(t) i(t) s(t) SL’ i(t+1) s(t) SL SL SL’’ SRs SRs (a) (b) (c) OL i(t+1) i(t) SRs’ s(t) NSYSU CSE SL SL OL i(t) i(t+1) s(t) PRs pipelined circuit SRs SRs (d) (e) (f) 2002/9 CRs 12

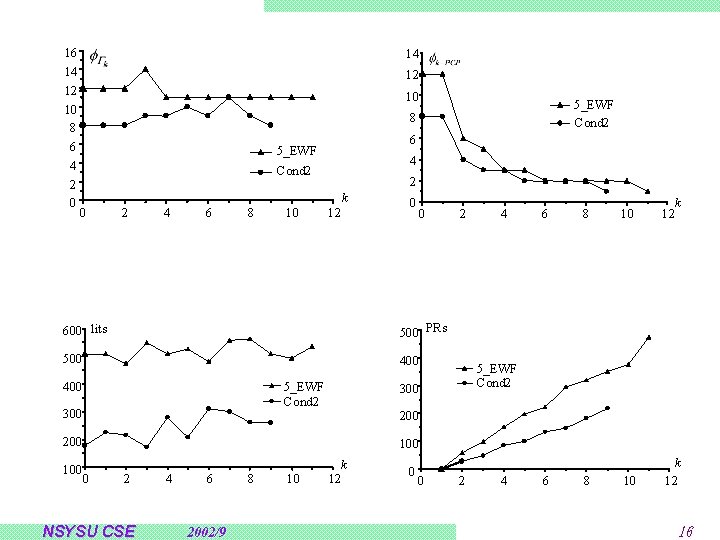
Pipelined Control Path Synthesis Approach Proposed Control Path Synthesis Approach A problem: may violate the control dependency Modify the original BSTG by inserting no operation states Theorem A BSTG satisfies all control dependencies if the distance Dij of states in each produce-consume state pair <Si, Sj>c satisfies one of the following conditions: Condition 1: if Sj is not a branch state, then Dij k. Condition 2: if Sj is a branch state, then Dij 2 k-1. Nij : the minimal number of NOOPs needed to insert between <Si, Sj>c Nij = 2 k-Dij-1, Nij = k-Dij, if Sj is a branch state; otherwise. Minimize the number of NOOPs using ILP formulation NSYSU CSE 2002/9 13

SCDFG BSTG +1 >1 [>2, -2] -2 >2 +3 +4 +5 -6 >3 +7 -9 -8 +10 [>3, +3] c 1 S 4 [+4] c 2 S 5 2 [>3, +3] c 1 S 4 c 2 S 5 [+5] [+4] 2 c 1 [c 3: +7] S 7 [c 3: -9] 1 c 2 [-6] S 6 [+11] NSYSU CSE 2 [>2, -2] S 3 2002/9 S 2 c 1 c 2 >1 >2 c 3 >3 S 6 [c 3: +7] S 7 [c 3: -9] [c 3: -8] S 8 [c 3: +10] [+11] S 9 [>1, +1] S 2 c 2 [-6] [+5] +11 S 1 [>1, +1] [c 3: -8] S 8 [c 3: +10] S 9 2 v 1 v 3 2 2 v 4 1 v 2 (a) i 1 i 2 2 v 1 v 3 2 2 v 4 1 (b) 14

[>1, +1] [>2, -2] S 1 [>1, +1] S 2 [>2, -2] S 1 S 2 N 1 N 2 c 1 S 3 [>3, +3] c 1 S 4 N 3 S 5 [+5] S 4 N 4 [+4] c 2 [-6] [c 3: -8] [c 3: +10] [>3, +3] c 1 c 2 c 1 S 8 S 5 [+5] [-6] [c 3: +7] S 7 [c 3: -9] S 6 [+11] S 9 pipelined circuit PR 3 PR 1 PR 2 CL 3 CL 1 N 3 N 4 [+4] [c 3: +7] S 7 [c 3: -9] S 6 [+11] N 1 N 2 c 1 S 9 [c 3: -8] S 8 [c 3: +10] control registers PRk-1 CLk state registers NSYSU CSE 2002/9 15

16 14 12 10 8 6 4 2 0 14 12 10 5_EWF Cond 2 8 6 5_EWF 4 Cond 2 2 k 0 2 4 6 8 10 12 0 0 600 lits 500 PRs 500 400 5_EWF Cond 2 300 4 6 8 10 k 12 5_EWF Cond 2 300 200 100 0 2 100 2 NSYSU CSE 4 6 2002/9 8 10 k 12 0 0 2 4 6 8 16

Dynamic Pipelining Approach Pipelining In most of existing pipelining techniques, latency is fixed or has some fixed values In some loops of ASICs, variant loop execution length and timerelative data dependencies between the different iterations make them to be pipelined inefficiently or impossibly Dynamic pipelining – A new loop scheduling approach to pipeline the loop using variant latencies – Controller consists of two interactive finite state machines NSYSU CSE 2002/9 while(c 1) { while(c 2) { } 17

Dynamic Pipelining Approach iteration Latency=5 Phase 1 Phase 2 Latency=6 Latency=4 Phase 3 i i+1 i+2 i+3 i+4 : the stages in which no operation is performed NSYSU CSE 2002/9 time 18

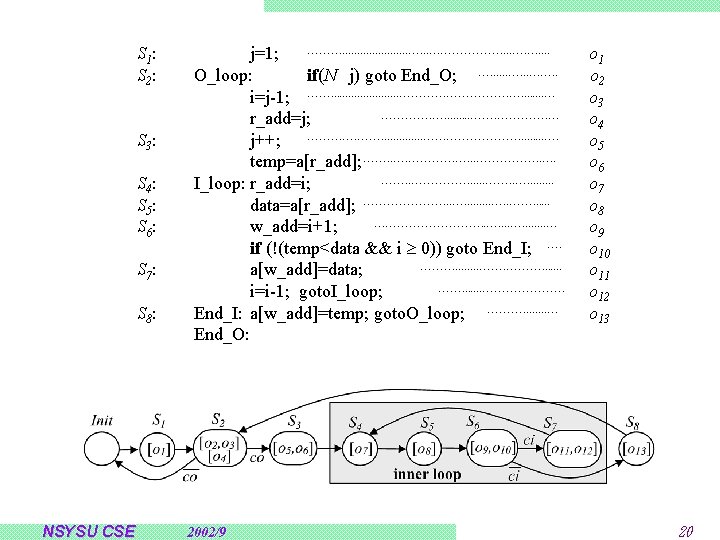
An Example of Dynamic Pipelining j=1; while (N>j) { /* N is the number of data which needs to be sorted */ i=j-1; temp=a[j]; while (temp<a[i] && i 0) { a[i+1]=a[i]; i=i-1; } a[i+1]=temp; j++; } NSYSU CSE 2002/9 19

BSTG Partitioning Init S 1 S 2 co S 3 Noopi co [start=1] done S 8 Noopo start S 4 S 6 S 5 [done=ci] done BSTGo done S 7 done start BSTGi Inner Loop Pipelining Noopo [done=1] PS 1 start S 6, i S 4, i done S 7, i S 5, i [done=ci] S 5, i+1 done S 4, i+1 original PBSTGi NSYSU CSE 2002/9 Noopo [done=1] start done S 6, i [done=ci] PS 2 done S 4, i+1 S 7, i S 5, i+1 new PBSTGi 21

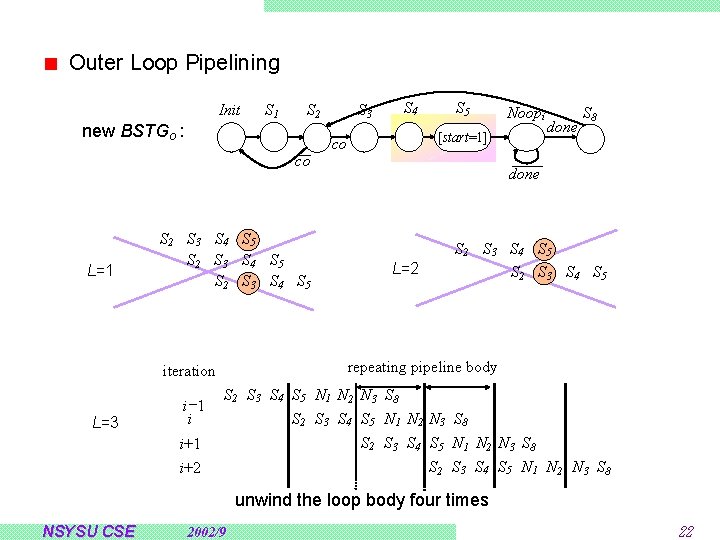
Outer Loop Pipelining Init S 1 S 2 new BSTGo : co L=1 S 2 S 3 S 4 S 5 L=3 S 4 S 5 Noopi [start=1] co done S 8 done L=2 S 3 S 4 S 5 S 2 S 3 S 4 S 5 repeating pipeline body iteration i -1 i S 3 S 2 S 3 S 4 S 5 N 1 N 2 N 3 S 8 i+1 i+2 S 3 S 4 S 5 N 1 N 2 N 3 S 8 S 2 S 3 S 4 S 5 N 1 N 2 N 3 S 8 unwind the loop body four times NSYSU CSE 2002/9 22

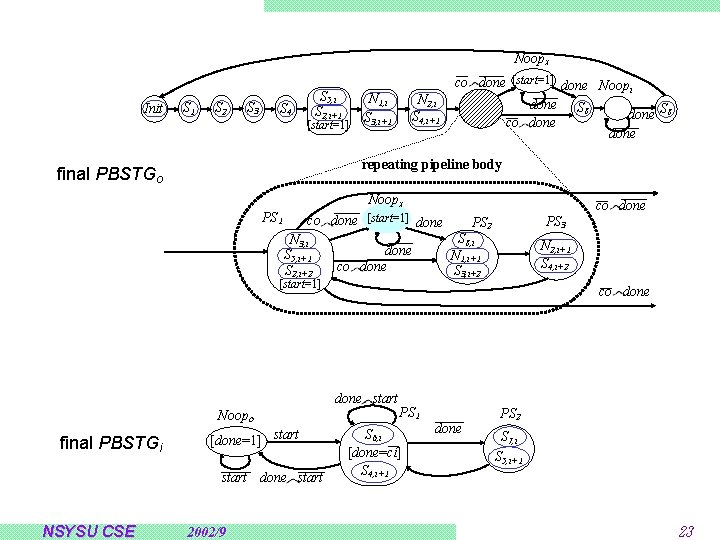
Noopx Init S 1 S 2 S 3 S 4 S 5, i S 2, i+1 N 1, i S 3, i+1 [start=1] N 2, i S 4, i+1 co done [start=1] done Noopi done S 8 co done repeating pipeline body final PBSTGo Noopx PS 1 N 3, i S 5, i+1 S 2, i+2 done co done [start=1] Noopo [done=1] start done start NSYSU CSE 2002/9 PS 3 PS 2 S 8, i N 1, i+1 S 3, i+2 N 2, i+1 S 4, i+2 co done start final PBSTGi co done [start=1] done PS 1 S 6, i [done=ci] S 4, i+1 done PS 2 S 7, i S 5, i+1 23

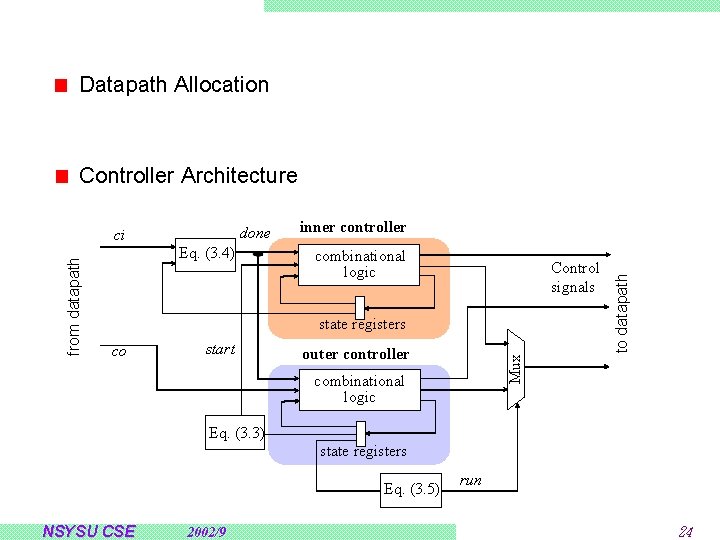
Datapath Allocation Controller Architecture combinational logic Control signals state registers co start outer controller Mux from datapath Eq. (3. 4) inner controller to datapath done ci combinational logic Eq. (3. 3) state registers Eq. (3. 5) NSYSU CSE 2002/9 run 24

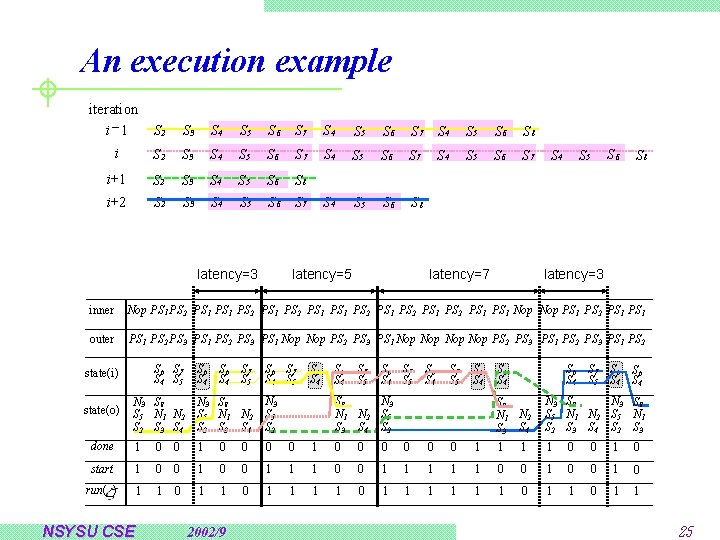
An execution example iteration i -1 S 2 S 3 S 4 S 5 S 6 S 7 S 4 S 5 S 6 S 8 i S 2 S 3 S 4 S 5 S 6 S 7 i+1 S 2 S 3 S 4 S 5 S 6 S 8 i+2 S 3 S 4 S 5 S 6 S 7 S 4 S 5 S 6 S 8 latency=5 latency=3 S 4 S 6 S 5 S 8 latency=3 latency=7 inner Nop PS 1 PS 2 PS 1 PS 2 PS 1 Nop PS 1 PS 2 PS 1 outer PS 1 PS 2 PS 3 PS 1 Nop Nop PS 2 PS 3 PS 1 PS 2 S 6 S 7 S 4 S 5 state(i) state(o) S 6 S 4 S 7 S 5 S 6 S 7 S 4 S 5 S 6 S 4 N 3 S 8 S 5 N 1 N 2 S 5 S 2 S 3 S 4 S 2 S 6 S 4 S 7 S 5 S 6 S 7 S 4 S 5 S 6 S 4 S 7 S 5 S 6 S 4 S 8 N 3 N 1 N 2 S 5 S 3 S 4 S 2 S 6 S 4 S 7 S 6 S 5 S 4 S 6 S 4 S 8 N 1 N 2 S 3 S 4 N 3 S 8 S 5 N 1 N 2 S 5 N 1 S 2 S 3 S 4 S 2 S 3 done 1 0 0 0 0 1 1 0 0 1 0 start 1 0 0 1 1 1 0 0 1 0 run( ) 1 1 0 1 1 0 1 1 NSYSU CSE 2002/9 25

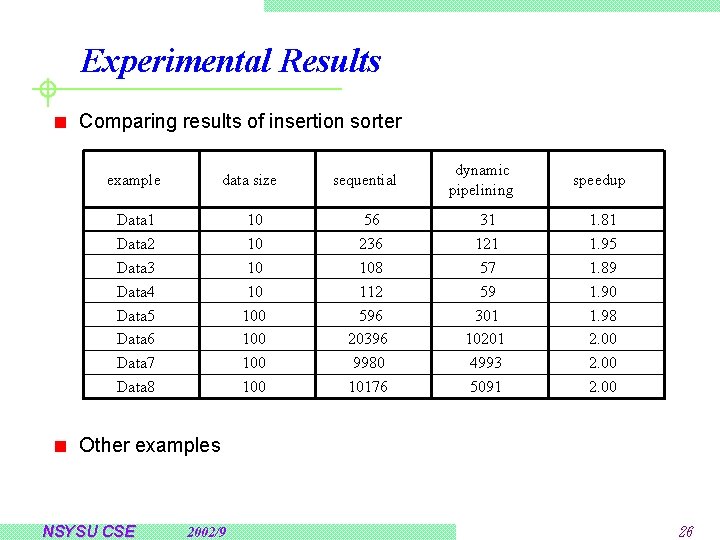
Experimental Results Comparing results of insertion sorter example data size sequential dynamic pipelining speedup Data 1 Data 2 Data 3 10 10 10 56 236 108 31 121 57 1. 81 1. 95 1. 89 Data 4 Data 5 Data 6 Data 7 Data 8 10 100 100 112 596 20396 9980 10176 59 301 10201 4993 5091 1. 90 1. 98 2. 00 Other examples NSYSU CSE 2002/9 26

Binary Arithmetic Coder Adaptive Binary Arithmetic Coder Q-coder: compress mainly bilevel image data a compression chip universal enough quickly compress any type of data that could still achieve a good compression ratio proposed modified hardwared algorithm – a new probability estimation modeler using a table-look-up approach – a technique solves carry-over and source termination – fixed-width parallel multiplier VLSI chip NSYSU CSE 2002/9 27

Encoding Algorithm Encoding() { C=0 x 00; A=0 xff; R=0 x 0000; S=00000; for (each input binary symbol) { phase 1: Generate P('0'|S) by Eq. (4. 5); phase 2: AP=A* P('0'|S); if (input symbol=='0') A=AP; else { A=A-AP; C=C+AP; if (carry occurs) R++; } Update the adaptive modeler by Eq. (4. 6); Shift the input symbol into S; phase 3: while (MSB of A==0) normalization_of_encoding(); } Encode LPS and then output 17 consecutive '1'’s; } NSYSU CSE 2002/9 28

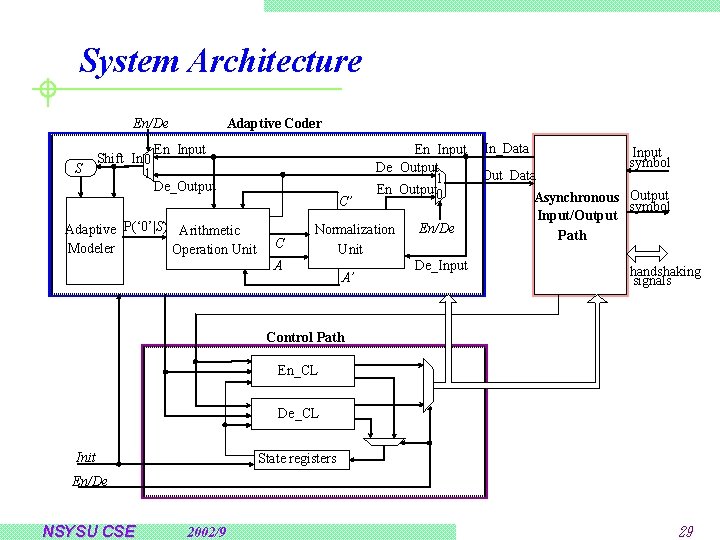
System Architecture En/De S Shift_In 0 1 Adaptive Coder En_Input De_Output Adaptive P(‘ 0’|S) Arithmetic Modeler Operation Unit C’ C En_Input De_Output 1 En_Output 0 Normalization Unit A A’ En/De De_Input In_Data Out_Data Input symbol Asynchronous Output symbol Input/Output Path handshaking signals Control Path En_CL De_CL Init State registers En/De NSYSU CSE 2002/9 29

NSYSU CSE 2002/9 30

NSYSU CSE 2002/9 31

Dynamic Pipelining Design NSYSU CSE 2002/9 32

Low-Error Fixed-Width Multipliers Fixed-Width Multiplier multiplication operations used in many ASICs have the special fixed-width property directly omit about half the adder cells of the conventional parallel multiplier a significant error would be introduced in the product Low-Error Fixed-Width Multiplier low-error fixed-width sign-magnitude multipliers low-error fixed-width two’s complement multipliers reduced width multiplier (n < m < 2 n) NSYSU CSE 2002/9 33

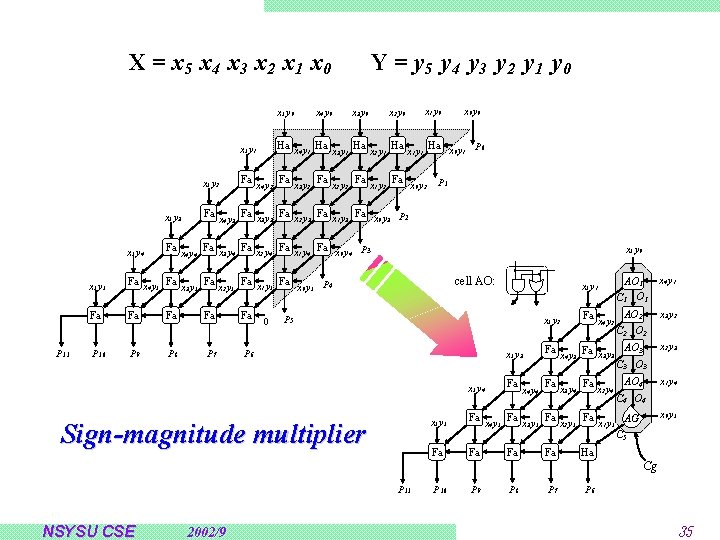
Low-Error Fixed-Width Multipliers Fixed-width sign-magnitude multipliers ê êë ú úû where Theorem: Given a , we have that and NSYSU CSE 2002/9 34

X = x 5 x 4 x 3 x 2 x 1 x 0 x 4 y 0 x 5 y 0 P 11 Y = y 5 y 4 y 3 y 2 y 1 y 0 x 3 y 0 x 1 y 0 x 2 y 0 x 0 y 0 x 5 y 1 Ha x 4 y 1 Ha Ha x 0 y 1 P 0 x 3 y 1 x 1 y 1 x 2 y 1 x 5 y 2 Fa Fa x 5 y 3 Fa Fa x 3 y 3 Fa x 2 y 3 Fa x 1 y 3 Fa x 0 y 3 P 2 x 5 y 4 Fa Fa x 3 y 4 Fa x 2 y 4 Fa x 1 y 4 Fa x 0 y 4 P 3 x 5 y 5 Fa Fa P 10 P 9 P 8 P 7 P 6 x 4 y 5 x 4 y 4 x 3 y 5 Fa x 4 y 3 x 2 y 5 x 4 y 2 x 3 y 2 Fa x 2 y 2 Fa x 1 y 2 Fa x 0 y 2 P 1 x 5 y 0 cell AO: Fa x 1 y 5 Fa x 0 y 5 P 4 0 AO 1 C 1 O 1 x 4 y 1 AO 2 C 2 O 2 x 3 y 2 Fa x 3 y 3 AO 3 C 3 O 3 x 2 y 3 Fa x 3 y 4 Fa x 2 y 4 AO 4 C 4 O 4 x 1 y 4 Fa x 0 y 5 x 5 y 1 P 5 x 5 y 2 x 5 y 3 Sign-magnitude multiplier x 5 y 4 Fa x 5 y 5 Fa Fa x 4 y 5 Fa x 4 y 4 x 3 y 5 Fa Fa x 4 y 3 x 2 y 5 Fa x 4 y 2 Fa x 1 y 5 AG C 5 Ha Cg P 11 NSYSU CSE 2002/9 P 10 P 9 P 8 P 7 P 6 35

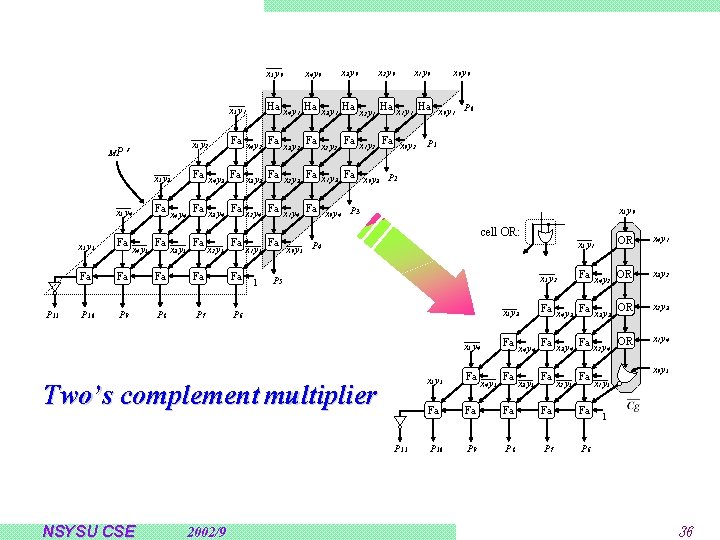
x 4 y 0 x 5 y 0 x 1 y 0 x 2 y 0 x 0 y 0 x 5 y 1 Ha x 4 y 1 Ha Ha x 0 y 1 P 0 x 3 y 1 x 1 y 1 x 2 y 1 x 5 y 2 Fa Fa x 5 y 3 Fa Fa x 3 y 3 Fa x 2 y 3 Fa x 1 y 3 Fa x 0 y 3 P 2 x 5 y 4 Fa Fa x 3 y 4 Fa x 2 y 4 Fa x 1 y 4 Fa x 0 y 4 P 3 x 5 y 5 Fa Fa P 10 P 9 P 8 P 7 P 6 MP’ P 11 x 3 y 0 x 4 y 5 x 4 y 4 x 3 y 5 Fa x 4 y 3 x 2 y 5 Fa x 4 y 2 x 1 y 5 1 Fa x 3 y 2 Fa x 2 y 2 Fa x 1 y 2 Fa x 0 y 2 x 5 y 0 cell OR: x 0 y 5 OR x 4 y 1 x 5 y 2 Fa OR x 3 y 2 x 5 y 3 Fa Fa x 3 y 3 OR x 2 y 3 x 5 y 4 Fa Fa x 3 y 4 Fa x 2 y 4 OR x 1 y 4 x 5 y 5 Fa Fa P 10 P 9 P 8 P 7 P 6 P 5 P 11 2002/9 x 5 y 1 P 4 Two’s complement multiplier NSYSU CSE P 1 x 4 y 5 x 4 y 4 x 3 y 5 Fa x 4 y 3 x 2 y 5 Fa x 4 y 2 x 0 y 5 x 1 y 5 1 36

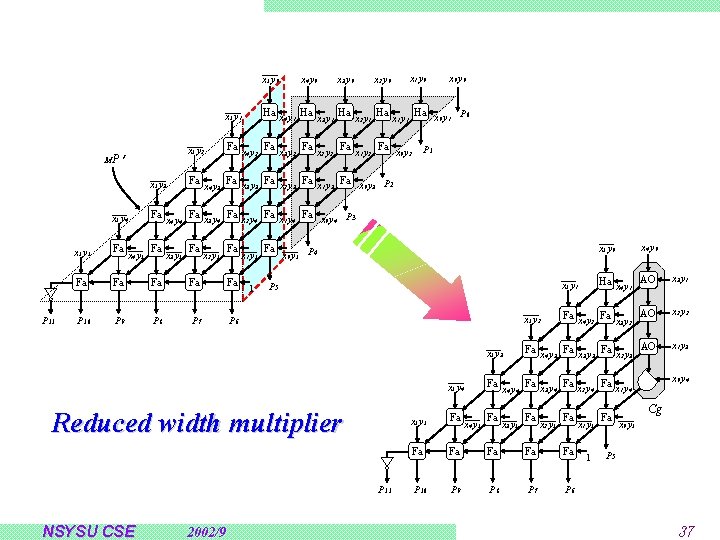
x 4 y 0 x 5 y 0 x 2 y 0 x 1 y 0 x 0 y 0 x 5 y 1 Ha x 4 y 1 Ha Ha x 0 y 1 P 0 x 3 y 1 x 1 y 1 x 2 y 1 x 5 y 2 Fa Fa x 5 y 3 Fa Fa x 3 y 3 Fa x 2 y 3 Fa x 1 y 3 Fa x 0 y 3 P 2 x 5 y 4 Fa Fa x 3 y 4 Fa x 2 y 4 Fa x 1 y 4 Fa x 0 y 4 P 3 x 5 y 5 Fa Fa P 10 P 9 P 8 P 7 P 6 MP’ P 11 x 3 y 0 x 4 y 5 x 4 y 4 x 3 y 5 Fa x 4 y 3 x 2 y 5 Fa x 4 y 2 x 1 y 5 1 Fa x 3 y 2 Fa x 2 y 2 Fa x 1 y 2 Fa x 5 y 1 Ha x 4 y 1 AO x 3 y 1 x 5 y 2 Fa Fa AO x 2 y 2 x 5 y 3 Fa Fa x 3 y 3 Fa x 2 y 3 AO x 1 y 3 x 5 y 4 Fa Fa x 3 y 4 Fa x 2 y 4 Fa x 1 y 4 x 5 y 5 Fa Fa P 10 P 9 P 8 P 7 P 6 P 5 P 11 2002/9 x 4 y 0 x 5 y 0 x 0 y 5 P 4 Reduced width multiplier NSYSU CSE P 1 x 0 y 2 x 4 y 5 x 4 y 4 x 3 y 5 Fa x 4 y 3 x 2 y 5 Fa x 4 y 2 x 1 y 5 1 Fa x 3 y 2 x 0 y 4 Cg x 0 y 5 P 5 37

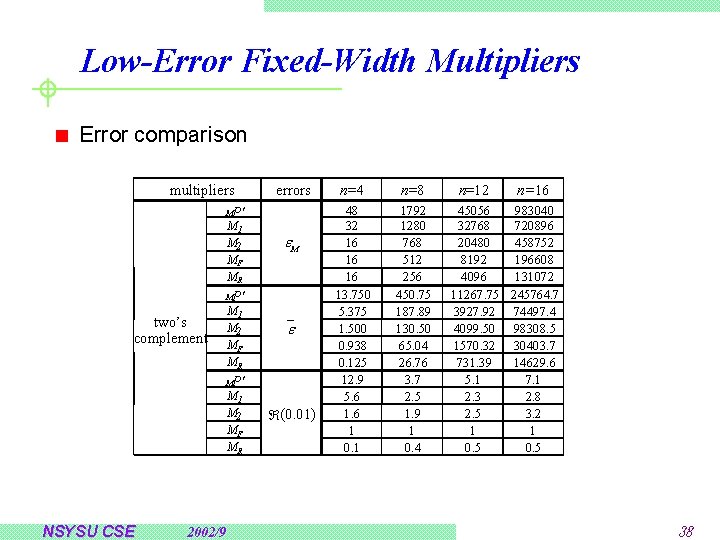
Low-Error Fixed-Width Multipliers Error comparison multipliers MP' M 1 M 2 MF MR errors e. M P' M M 1 M 2 MF MR two’s complement e P' M M 1 M 2 MF MR NSYSU CSE 2002/9 (0. 01) n=4 n=8 48 32 16 16 16 13. 750 5. 375 1. 500 0. 938 0. 125 12. 9 5. 6 1 0. 1 1792 1280 768 512 256 450. 75 187. 89 130. 50 65. 04 26. 76 3. 7 2. 5 1. 9 1 0. 4 n=12 n=16 45056 983040 32768 720896 20480 458752 8192 196608 4096 131072 11267. 75 245764. 7 3927. 92 74497. 4 4099. 50 98308. 5 1570. 32 30403. 7 731. 39 14629. 6 5. 1 7. 1 2. 3 2. 8 2. 5 3. 2 1 1 0. 5 38

Application (a) original (d) MR 1 NSYSU CSE 2002/9 (b) M 1 (c) MF (e) MR 2 (f) MS 39

(a) original NSYSU CSE 2002/9 (b) M 1 40

(c) MF NSYSU CSE 2002/9 (d) MR 1 41

(e) MR 2 NSYSU CSE 2002/9 (f) MS 42

Fuzzy Color Corrector Fuzzy Color Correction in previous literature, the color correction process was modeled as a three-level fuzzy tree inference process – the algorithm in it is inefficient and its hardware implementation is then costly and slow a new efficient fuzzy tree inference algorithm suitable for the center of gravity defuzzification method is proposed NSYSU CSE 2002/9 43

modified fuzzy color correction algorithm Init: L=1; S 1: while (input pattern Xi NULL) { S 1: Calculate the address of rule memory (ROM); S 2, S 3: s 1=ROM[address++]; D=s 1; S 4: k=0; Path. L=0; d=ROM[address]; S 5: while (k<8 && D>0) { S 6: D=d; Path. L=k; k++; } S 5: if (1 k 7 && |D| d/2) Path. L=k; S 7~S 13: Calculate Xo using Eq. (6. 6); S 7: if (++L==4) L=1; } NSYSU CSE 2002/9 44

2. 5. Fuzzy Color Corrector Proposed Sequential Architecture NSYSU CSE 2002/9 45

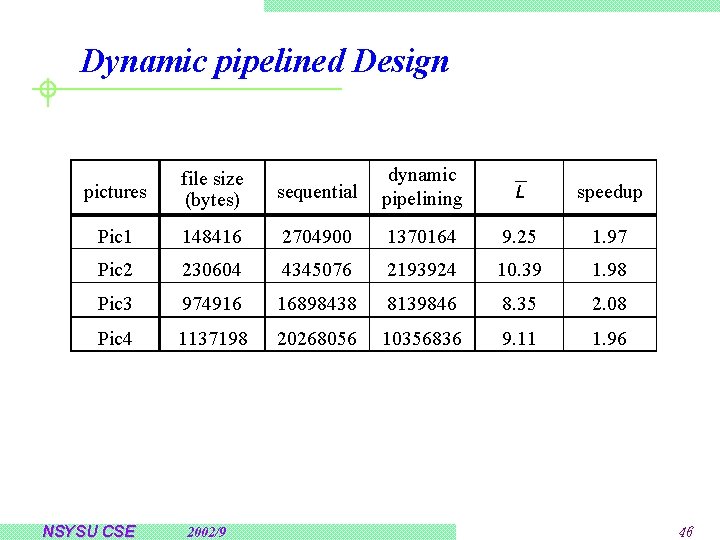
Dynamic pipelined Design sequential dynamic pipelining L speedup 148416 2704900 1370164 9. 25 1. 97 Pic 2 230604 4345076 2193924 10. 39 1. 98 Pic 3 974916 16898438 8139846 8. 35 2. 08 Pic 4 1137198 20268056 10356836 9. 11 1. 96 pictures file size (bytes) Pic 1 NSYSU CSE 2002/9 46

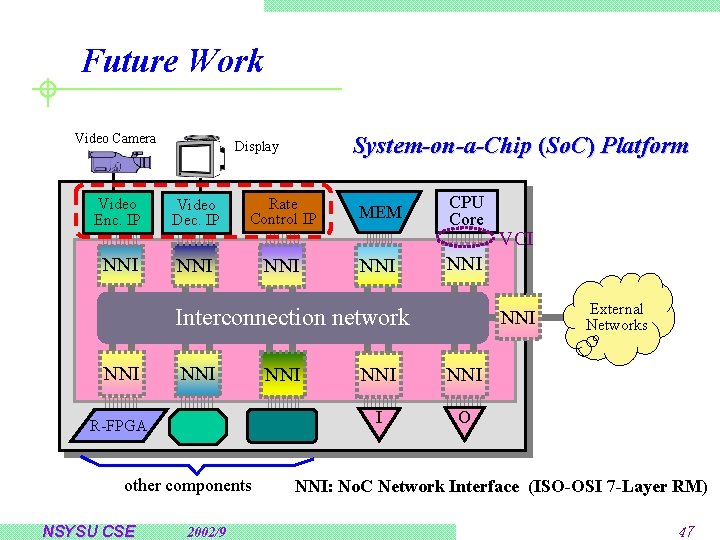
Future Work Video Camera System-on-a-Chip (So. C) Platform Display Video Enc. IP Video Dec. IP Rate Control IP MEM NNI NNI CPU Core NNI Interconnection network NNI R-FPGA other components NSYSU CSE 2002/9 NNI VCI NNI NNI I O External Networks NNI: No. C Network Interface (ISO-OSI 7 -Layer RM) 47

References [1] Jer-Min Jou, Shiann-Rong Kuang, Yeu-Horng Shiau, and Ren-Der Chen, “Design of A Dynamic Pipelined Architecture for Fuzzy Color Correction”, to be published in IEEE Transactions on VLSI Systems, 2002. [2] Jer-Min Jou, Yeu-Horng Shiau, Pei-Yin Chen, and Shiann-Rong Kuang, “A Low Cost Gray Prediction Search Chip for Motion Estimation”, Vol. 49, No. 7, pp. 928 -938, July 2002. [3] Shiann-Rong Kuang, Jer-Min Jou, Ren-Der Chen, and Yeu-Horng Shiau, “Dynamic Pipeline Design of an Adaptive Binary Arithmetic Coder, ” IEEE Transactions on Circuits & Systems Part II, Vol. 48, No. 9, pp. 813 -825, September 2001. [4] Jer Min Jou, Shiann Rong Kuang, and Ren-Der Chen, “Design of Low-Error Fixed-Width Multipliers for DSP Applications, ” IEEE Transactions on Circuits & Systems Part II, Vol. 46, No. 6, pp. 836 -842, June 1999. NSYSU CSE 2002/9 48

References [5] Jer-Min Jou, Shiann-Rong Kuang, and Ren-Der Chen, “A New Efficient Fuzzy Algorithm for Color Correction, ” IEEE Transactions on Circuits & Systems Part I, Vol. 46, No. 6, pp. 773 -775, June 1999. [6] Shiann-Rong Kuang, Jer-Min Jou, and Yuh-Lin Chen, “The Design of an Adaptive On-Line Binary Arithmetic Coding Chip, ” IEEE Transactions on Circuits & Systems Part I, Vol. 45, No. 7, pp. 693706, July 1998. [7] Jer-Min Jou and Shiann-Rong Kuang, “Design of a low-error fixedwidth multiplier for DSP applications, ” Electronics Letters, Vol. 33, No. 19, pp. 1597 -1598, 1997. [8] Jer-Min Jou and Shiann-Rong Kuang, “A Library-Adaptively Integrated High Level Synthesis System, ” Proceedings of NSC – Part A: Physical Science and Engineering, Vol. 19, No. 3, pp. 220234, May 1995. NSYSU CSE 2002/9 49