The Derivative and Tangent Line Problem Section 2

The Derivative and Tangent Line Problem Section 2. 1 AP Calc

Given two points on f(x) how do you find the slope of the secant line between them?

Definition: Tangent Line with slope m If f is defined on an open interval containing c, and if the limit, exists, then the line passing through (c, f(c)) with slope m is the tangent line to the graph of f at point (c, f(c)).

Find the slope of the tangent line of y=3 x-4 at the point (6, 14).

Find the slopes of the tangent lines to the graph g(x)=5 -x².

Find the equation of the tangent line of at (-1, -2).

Definition: Derivative of a Function The derivative of f at x is given by provided the limit exists. For all x for which the limit exists, f’ is a function of x.

The process of finding a derivative = differentiation

Find the derivative using the limit process: f(x)=1 - x²

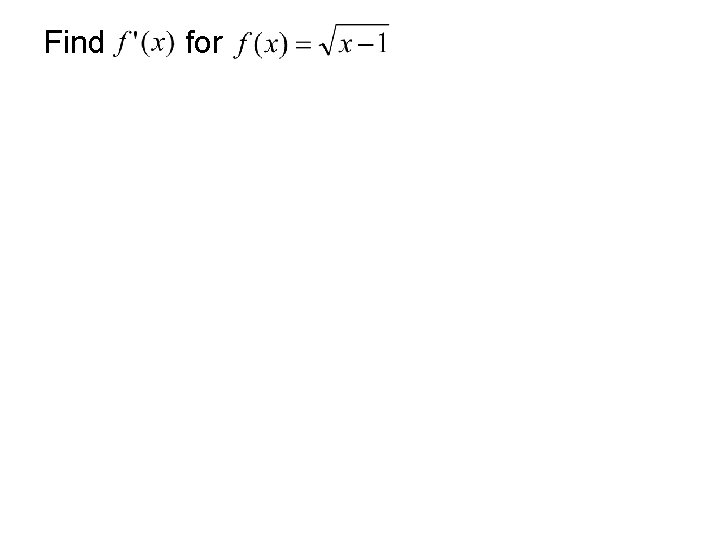
Find for

Find the derivative with respect to t for the function y = t² + 2 t + 1

Alternative limit form of the derivative:

The function must be differentiable from the left and the right: (these limits must both exist and be equal)

f is differentiable on the closed interval [a, b] if it is differentiable on (a, b) and if the derivative from the right at a and from the left at b both exist.

If a function is not continuous at x=c, then it is not differentiable at x=c.

Use the alternate form to find the derivative at x=c for , when c=-5.

Look at the greatest integer function on page 100

Given Is the function continuous at x=4? Find Vertical Tangent, not differentiable

Thm 2. 1 Differentiability Implies Continuity If f is differentiable at x=c, then f is continuous at x=c. Contrapositive also true: If f is not continuous, then it is not differentiable.

It is possible to have a function that is continuous, but not differentiable.