The Death of a High Mass Star n

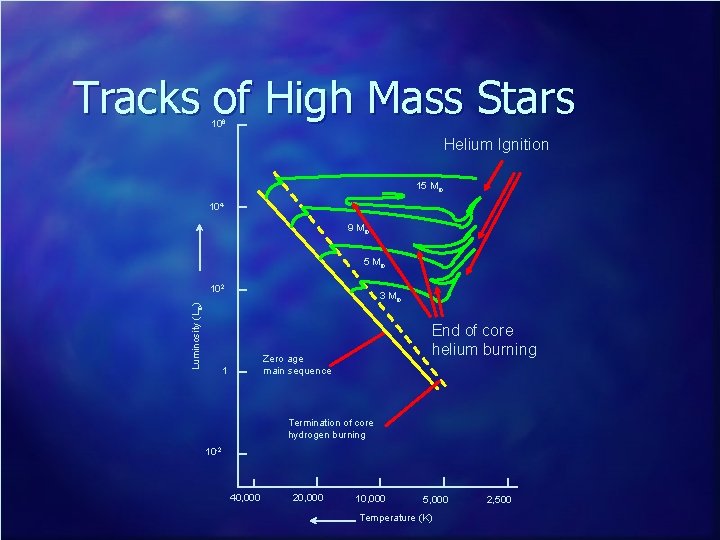
The Death of a High Mass Star n Evolution of a star greater than about 4 solar masses post helium ignition – The star moves roughly horizontally across the Hertzprung-Russell diagram n Crossing the instability strip, becoming a Cepeid variable – Helium burning produces carbon and oxygen “ash”

Tracks of High Mass Stars 106 Helium Ignition 15 M¤ 104 9 M¤ 5 M¤ Luminosity (L¤) 102 3 M¤ End of core helium burning Zero age main sequence 1 Termination of core hydrogen burning 10 -2 40, 000 20, 000 10, 000 5, 000 Temperature (K) 2, 500

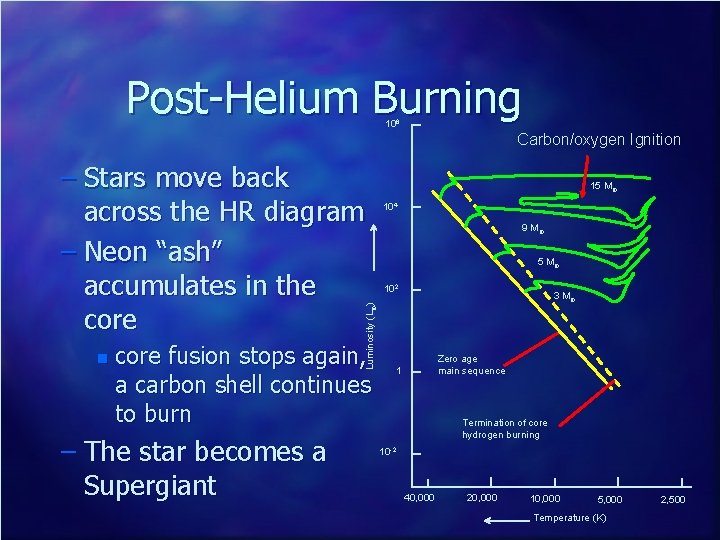
Post-Helium Burning n For stars above about 4 solar masses – the degenerate carbon-oxygen core can exceed the Chandrasekhar Limit Degeneracy pressure can no longer support the core n Core collapse resumes n – Pressures and densities become sufficient to burn carbon n core collapse temporarily halted

Post-Helium Burning 106 Carbon/oxygen Ignition n Luminosity (L¤) – Stars move back across the HR diagram – Neon “ash” accumulates in the core fusion stops again, a carbon shell continues to burn – The star becomes a Supergiant 15 M¤ 104 9 M¤ 5 M¤ 102 3 M¤ Zero age main sequence 1 Termination of core hydrogen burning 10 -2 40, 000 20, 000 10, 000 5, 000 Temperature (K) 2, 500

Post-Helium Burning n Note that: – At the cessation of each phase of core burning, the star moves to the red giant region – On ignition of a new source of core fuel, the star moves back across the HR diagram – The star eventually consists of a number of concentric shells at different stages of burning

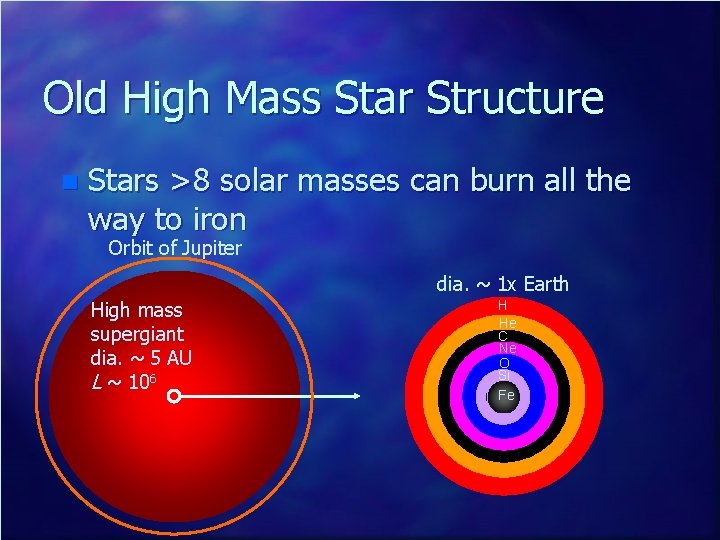
Old High Mass Star Structure n Stars >8 solar masses can burn all the way to iron Orbit of Jupiter dia. ~ 1 x Earth High mass supergiant dia. ~ 5 AU L ~ 106 H He C Ne O Si Fe

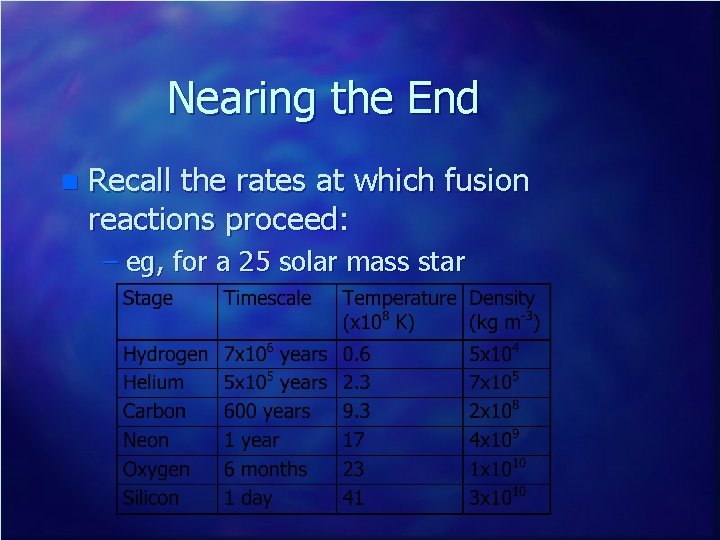
Nearing the End n Recall the rates at which fusion reactions proceed: – eg, for a 25 solar mass star

Nearing the End n The star shown earlier is in its last day – What events occur next? – What is the timescale? – What are the consequences?

Core Collapse n If a star fails to lose mass by other means. . . – e. g. , via shell ejection as for low mass stars …The iron core can reach the Chandrasekhar limit n The subsequent events lead to the destruction of the star n

Core Collapse n No nuclear processes can release energy from iron – Two mechanisms for absorbing energy: Photodisintegration of nuclei n Electron capture by protons – As with the initial stages of star formation, there is now nothing to oppose free-fall under gravity n

Core Collapse n The free-fall collapse time of the core is very short – with a density of about 1012 kgm-3, the core can collapse in ~ 1 ms n Temperature rises to ~5 x 109 K – g radiation sufficiently energetic to photodissociate 56 Fe to He

Core Collapse – g + 56 Fe « 134 He + 4 n absorbs 124. 4 Me. V n About 75% dissociated n

Core Collapse n As temperatures and densities rise, He nuclei can dissociate – g + 4 He « 2 p + 2 n n All the fusion in the core is now undone – Total energy absorbed by a collapsing Chandrasekhar mass iron core ~ 1045 J – Equivalent to the energy output of the sun over 1010 years!

Core Collapse n Densities continue to rise – The electron gas is definitely degenerate by this time – Recall from a workshop that the momentum of an electron at the fermi energy, Ef , is given by:

Core Collapse – The energy of an electron at the Fermi Surface is: – If this energy becomes greater than 1. 3 Me. V, inverse b decay can occur: – e- + p ® n + n e – This becomes possible at densities ~1014 kgm-3

Core Collapse n Neutrinos interact weakly with matter – Hence escape rapidly from the contracting core – For a core with the Chandrasekhar Mass, we have ~1057 electrons and protons – Hence the core loses ~1. 6 x 1045 J – Neutrino pulse produced over a few seconds

Core Collapse n Core collapse is now only halted when the core reaches the density of atomic nuclei – ~1017 kgm-3

A Supernova – The shockwave produced from the core bounce disrupts the outer layers of the star – The star’s luminosity leaps to ~108 solar luminosities – The gravitational energy released by the core collapse is ~1046 J ~2 x 1045 J absorbed by iron disintegration and inverse b decay n ~1044 J in debris kinetic energy n ~1042 J in optical energy in first year n

A Supernova n Remainder of the energy contained within a hot, bloated remnant neutron star – Density ~ 1014 kgm-3, typical temp. ~1011 K A dense plasma of neutrons, protons, other nuclei, electrons, photons and neutrinos n Essentially opaque to radiation n Remaining energy loss via neutrinos (mainly neutrino-antineutrino pair production) n

Supernova Remnants n Typically a rapidly expanding nebula is produced – e. g. , the Crab Nebula, produced in a supernova explosion in 1054

Supernova Remnants n The collapsed core remains as a neutron star – What are the properties of such objects? Density? n Temperature? n Is there an upper limit to their mass? n How do they appear n

Stellar Remnants n White Dwarfs Originate from low mass stars n Mass less than the Chandrasekhar limit n Supported by the pressure of a degenerate electron gas n n Neutron Stars Originate from high mass stars n Mass may be greater than the Chandrasekhar Limit n Supported by nuclear forces n

White Dwarfs – Sirius B the first to be observed (1862) – Luminosities very low n ~10 -3 solar luminosities – Surface temperatures high n ~30, 000 K – Masses of the order of one solar mass n measured from orbital motions

White Dwarfs n Implications: – High temperature and low luminosity imply low radius - comparable with the Earth – Mass comparable to the sun implies high density - typically 109 kgm-3 – Electrons form a degenerate quantum gas

White Dwarfs n Pressure arises from: – Pauli Exclusion Principle – Heisenberg’s Uncertainty Principle n Given an electron density of n with a mean momentum p and velocity v , the pressure is:

White Dwarfs – A density n implies a mean spacing Dx = n-1/3 – Hence, from Heisenberg, the momentum, p, will be: p ~ Dp ~ h/Dx = hn 1/3 – The mean velocity is then (m = mass of electron): v = p/m ~ (h/m)n 1/3 – The pressure is therefore approximately: P = 1/3 nvp ~ 1/3 ((h 2/m)n 5/3

White Dwarfs – If the electrons are non-relativistic, the pressure is given exactly by (Lecture 5 and Physics of Stars secn 2. 2) – Using the density given earlier, this gives a typical pressure of 1016 atm.

White Dwarfs n Mass-Radius Relationship – To estimate the mass-radius relationship, we require an estimate of the pressure required to support the star: Gravitational acceleration acting on column ~ GM/R 2 Mass of column ~ r. R ~ M/R Hence P ~ GM 2/R 4 2 Unit area Weight of column of material = P R

White Dwarfs – Equating this pressure with that derived from degeneracy considerations we find: – Noting that n = r/mp and M ~ r. R 3 we obtain the proportionality: – Consequence: More massive white dwarfs are smaller!

White Dwarfs – As white dwarfs increase in mass, electrons are forced closer together n n Hence, in accordance with Heisenberg, their momenta increase Consequently, their speeds approach c and they become ultra-relativistic – The degeneracy pressure is now given by:

White Dwarfs – The pressure does not now rise fast enough to support the increase in gravity, and a maximum mass is achieved – The Chandrasekhar Mass, given by: – ~1. 4 solar masses

Neutron Stars n A stellar core exceeding this mass cannot form a white dwarf – Collapse continues until nuclear densities are reached – A neutron star is formed, supported by degeneracy pressure of neutrons – Again, R µ M-1/3 – Typical radius ~ 10 -20 km

Neutron Stars n Structure: – Not well known n Physics of “neutron matter” not well established

Neutron Stars n Other properties: – High gravitational fields n Escape velocity ~ 50%c – High magnetic fields n Concentrated fields from original star – High rotation rate Conservation of angular momentum n Typical rotational period for a new neutron star ~ 30 ms n

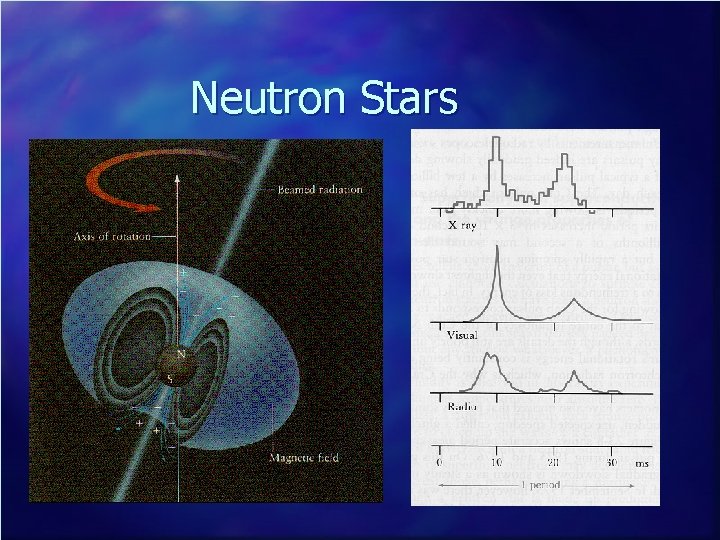
Neutron Stars n Pulsars – High magnetic fields lead to “beaming” of particles and radiation along magnetic poles – High spin rates lead to rapid “pulsing”

Neutron Stars

Neutron Stars n Other manifestation: – Synchrotron radiation from supernova remnants, implying strong magnetic fields and a power source

Neutron Stars n Spin rate slows with time – Due to loss of energy – The Crab pulsar is slowing at about 3 x 10 -8 s per day n Energy loss consistent with that required to power the Crab Nebula

Neutron Stars n Upper limit for mass – The properties of neutron star matter are not well known – Current estimates place the limit at about 2 -3 solar masses n n Find the mass (and hence the radius) at which the escape velocity = c Certainly no more than 5 – What happens to stellar cores above this limit?

Black Holes n Neutron degeneracy can no longer support the star – collapse resumes, with nothing now to support it – Escape velocity exceeds c light can no longer escape n sphere surrounding the collapsed star where the escape velocity = c is termed the Event n Horizon

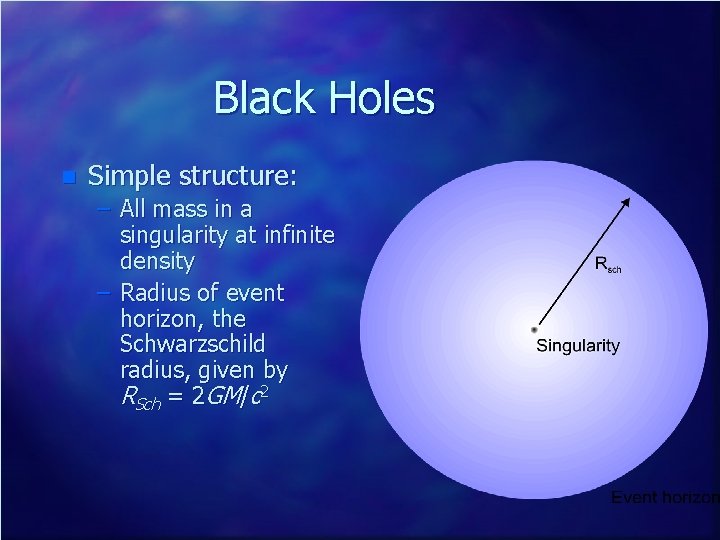
Black Holes n Simple structure: – All mass in a singularity at infinite density – Radius of event horizon, the Schwarzschild radius, given by RSch = 2 GM/c 2

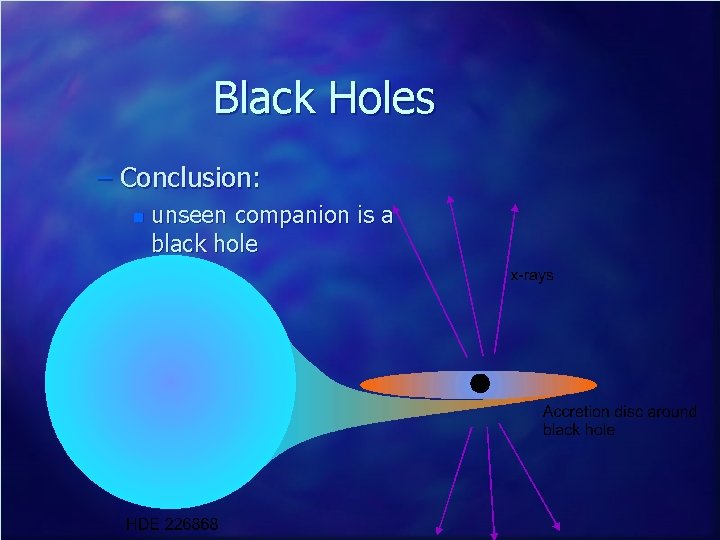
Black Holes n Cannot be directly seen – Indirect evidence n n n Strong x-ray source Cygnus X-1 “Flickers” on a timescale of 0. 01 s (hence small) Identified with a B 0 supergiant star, HDE 226868 Radio outbursts also occur Spectral shifts show this is a binary system with HDE 226868 having a mass of 30 solar masses and an invisible companion with mass 7 solar masses

Black Holes – Conclusion: n unseen companion is a black hole