The Critical Flow Function and Beyond Real Gas

The Critical Flow Function and Beyond (Real Gas Corrections for CFVs) Aaron Johnson National Institute of Standard and Technology Gaithersburg, MD 20899 CFV Measurement Conference September 20, 2013 Poitiers, France

Objectives 1) To suggest the use of REFPROP Thermodynamic Database for calculating C* 2) To introduce real gas corrections for large b = d/D applications 3) To present results experimentally from measuring C*

Outline • Background on CFV Theory & Definitions • Listing of Most Common Methods for computing C* Ø Approximate Analytical Techniques Ø Tables and Curve Fits Ø Thermodynamic databases • • • Overview of REFPROP Evaluation of various methods used for computing C* Real Gas Effects in large b = d/D Applications Measurement of C* Discussion

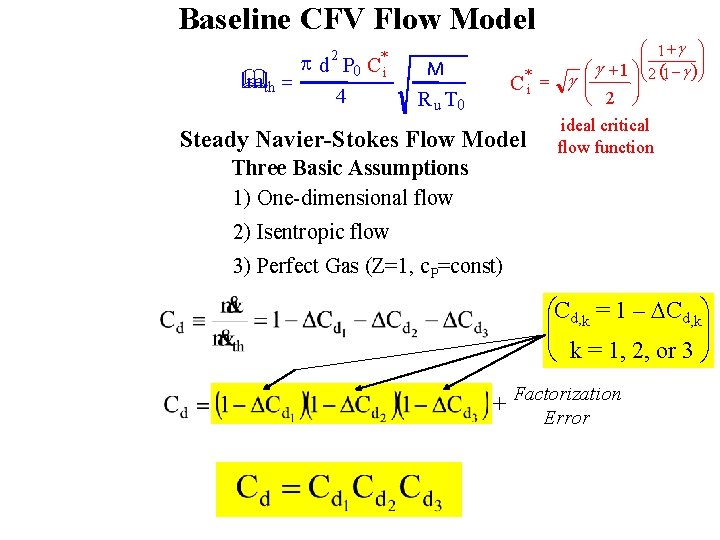
Baseline CFV Flow Model 2 * p d P 0 C i m th = & 4 M R u T 0 C*i = Steady Navier-Stokes Flow Model Three Basic Assumptions 1) One-dimensional flow æ 1 +g ö ç ÷ +1 öçè 2 (1 - g ) ÷ø ÷ æg è 2 ø g ç ideal critical flow function 2) Isentropic flow 3) Perfect Gas (Z=1, c. P=const) æCd, k = 1 – DCd, kö çç ÷÷ è k = 1, 2, or 3 ø + Factorization Error

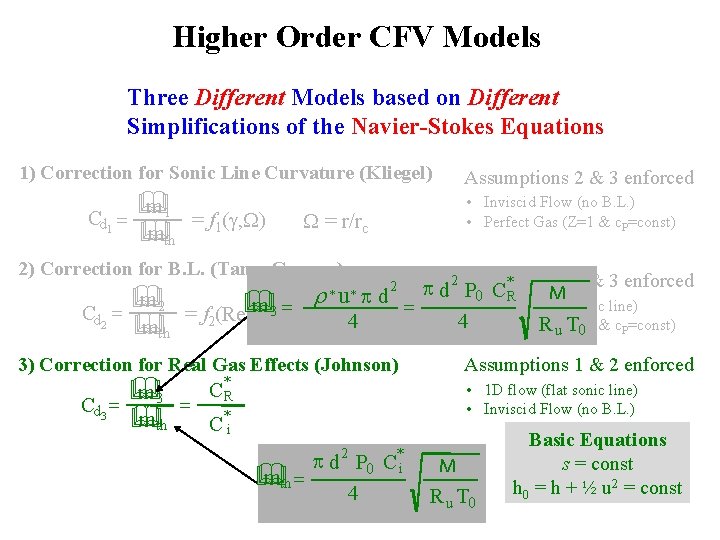
Higher Order CFV Models Three Different Models based on Different Simplifications of the Navier-Stokes Equations 1) Correction for Sonic Line Curvature (Kliegel) Cd 1 = m 1 & mth & = f 1(g, W) Cd 2 = • Inviscid Flow (no B. L. ) • Perfect Gas (Z=1 & c. P=const) W = r/rc 2) Correction for B. L. (Tang, Geropp) m 2 & mth & Assumptions 2 & 3 enforced r m & = 3 = f 2(Re, g, W) * 2 Assumptions 1 & 3 enforced * p d P C M 0 R u d = • 1 D flow (flat sonic line) 4 • Perfect Gas 4 R u(Z=1 T 0 & c. P=const) *p 2 3) Correction for Real Gas Effects (Johnson) Cd 3 = m 3 & mth & = Assumptions 1 & 2 enforced C*R • 1 D flow (flat sonic line) • Inviscid Flow (no B. L. ) C*i 2 * p d P 0 C i mth = & 4 M R u T 0 Basic Equations s = const h 0 = h + ½ u 2 = const

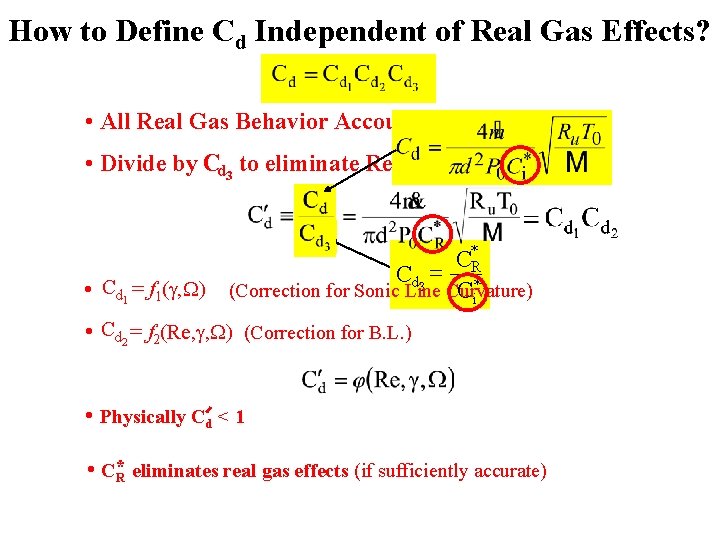
How to Define Cd Independent of Real Gas Effects? • All Real Gas Behavior Accounted for in Cd 3 • Divide by Cd 3 to eliminate Real Gas Effects C*R Cd 3 = * • Cd 1 = f 1(g, W) (Correction for Sonic Line Curvature) Ci • Cd 2 = f 2(Re, g, W) (Correction for B. L. ) • Physically Cd < 1 • C*R eliminates real gas effects (if sufficiently accurate)(

Numerous C* Models are Used by End Users • Accuracy between different models can vary significantly • Many C* models are tailored for a specific gas type Ø End user must acquire different models for each gas type • The numerous C* models can be confusing to end users Ø Functional expressions for C* based on approximate analytical solutions Ø Tables and Curve fits provided in CFV Standards (ISO 9300 and ASME) Ø Various published C* values for different gases • • • N 2, Air, CO 2, Ar, He, and others (R. C. Johnson 1965, NASA TND-2565 ) Steam (Owen & Amini, 1994 and 1997) wet air (Aschenbrenner, 1983, Britton et. al. 1998) dry & humid air, natural gas, methane and other gases (Sullivan, 1980’s) N 2, Ar, CH 4, dry & humid air, and natural gas (Stewart et. al. 1999, 2000) Tables of Thermodynamic and Transport Properties (Hilsenrath, 1960) Ø Thermodynamic Databases • • GERG (2004) AGA 8 (1992) AGA 10 (based on AGA 8, 2003) REFPROP 9. 1

Overview of REFPROP • REFPROP is an acronym for REFerence fluid PROPerties • Based on the most accurate pure fluid and mixture models currently available Ø Ø Maintained by NIST (Eric W. Lemmon) Continuously updated (next version is being developed) More than 50 pure fluids Flexibility to create your own mixture (e. g. , wet air, natural gas) • REFPROP 9. 1 Includes multiple Thermodynamic Databases Ø GERG-2004 Model (Prof. Dr. Wolfgang Wagner and Dr. Oliver Kunz) • 22, 000 experimental natural gas data and natural gas like multicomponent data Ø Modified GERG-2004 Model (Default Model in REFPROP) • NIST modified the original GERG model making it more accurate • Mixture parameters are identical to GERG Model • Pure fluid equations of state are more complex and more accurate Ø AGA 8 (1992) • REFPROP Platform and Interface Capabilities Ø Stand alone graphical user interface (GUI) Ø Compatible with Excel, Fortran, Visual Basic, C++, Mat. Lab, Lab. VIEW, Delphi • Computes over 75 Thermodynamic properties (gas, liquid, and two phase) Ø Density, Specific Heat, Enthalpy, Compressibility Factor, etc. Ø C* is one of the properties applicable to the gas phase for CFV flows

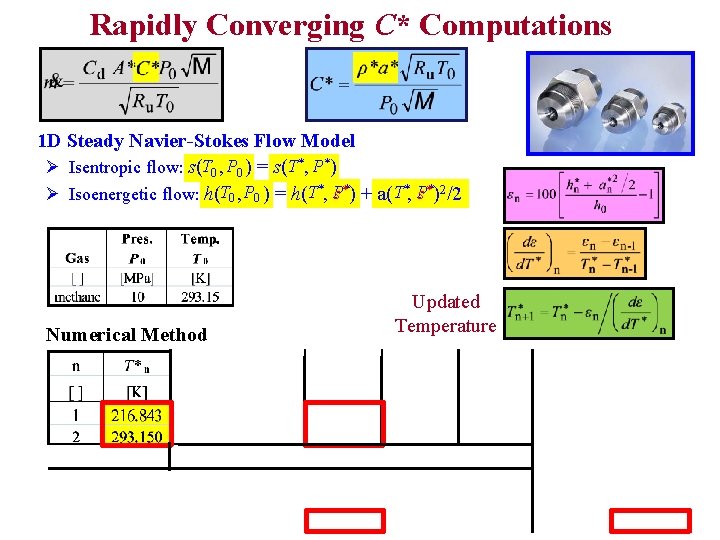
Rapidly Converging C* Computations 1 D Steady Navier-Stokes Flow Model Ø Isentropic flow: s(T 0 , P 0 ) = s(T* , P* ) Ø Isoenergetic flow: h(T 0 , P 0 ) = h(T*, Ps**) + a(T*, Ps**)2/2 Numerical Method Updated Temperature

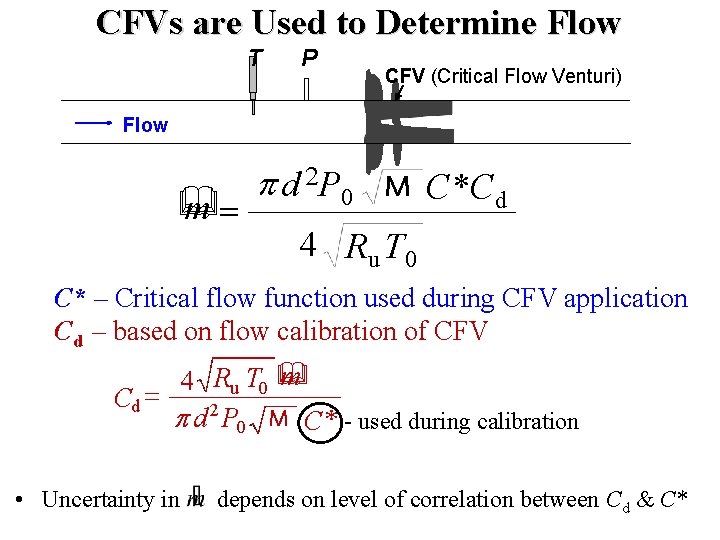
CFVs are Used to Determine Flow T P CFV (Critical Flow Venturi) Flow p d 2 P 0 M C* Cd & m= 4 R u T 0 C* – Critical flow function used during CFV application Cd – based on flow calibration of CFV m 4 Ru T 0 & Cd = p d 2 P 0 M C* - used during calibration • Uncertainty in m depends on level of correlation between Cd & C*

Definition of and Methods used for Computing C* 1 D Steady Navier-Stokes Flow Model Ø Isentropic flow: s(T 0 , P 0 ) = s( Tt , Pt ) Ø Isoenergetic flow: h(T 0 , P 0 ) = h( Tt , Pt ) + a(Tt , Pt )2/2 Model Thermo. Expressions Critical Flow Function Formula Ideal Gas Polytropic Process • REFPROP 8. 0 Real Gas • AGA 10 (AGA 10) • REFPROP 7. 0 (R 7) Tables Curve Fits Ø Modified GERG (R 8, NIST) Ø GERG (R 8, GERG) Ø AGA 8 (R 8, AGA) N/A Tables of Fits of • ISO 9300 CFV Standard (2005)

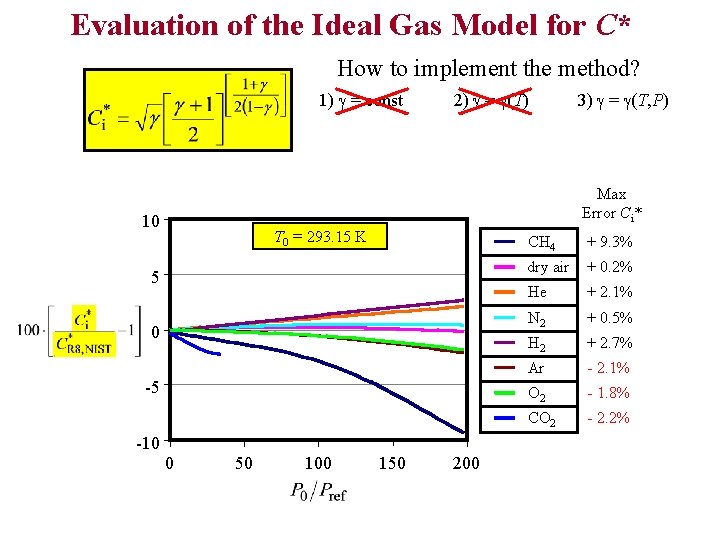
Evaluation of the Ideal Gas Model for C* How to implement the method? 1) g = const 2) g = g(T) 3) g = g(T, P) Max Error Ci* 10 T 0 = 293. 15 K Pref = 101. 325 k. Pa 5 0 -5 -10 0 50 100 150 200 CH 4 + 9. 3% dry air + 0. 2% He + 2. 1% N 2 + 0. 5% H 2 + 2. 7% Ar - 2. 1% O 2 - 1. 8% CO 2 - 2. 2%

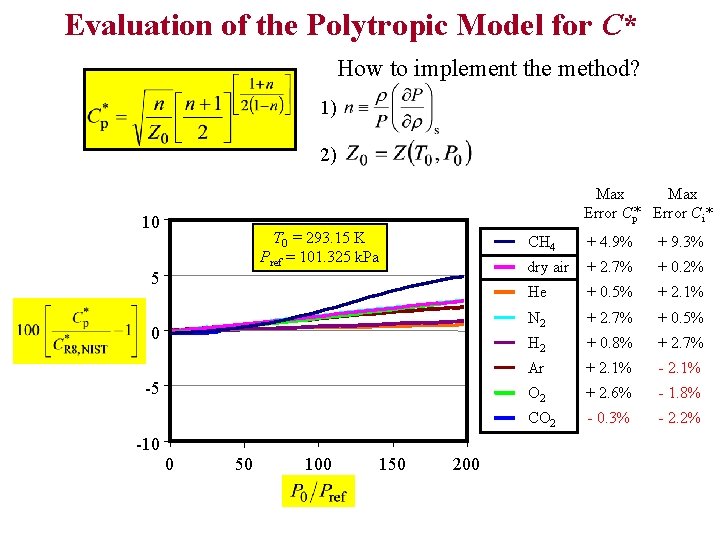
Evaluation of the Polytropic Model for C* How to implement the method? 1) 2) Max Error Cp* Error Ci* 10 T 0 = 293. 15 K Pref = 101. 325 k. Pa 5 0 -5 -10 0 50 100 150 200 CH 4 + 4. 9% + 9. 3% dry air + 2. 7% + 0. 2% He + 0. 5% + 2. 1% N 2 + 2. 7% + 0. 5% H 2 + 0. 8% + 2. 7% Ar + 2. 1% - 2. 1% O 2 + 2. 6% - 1. 8% CO 2 - 0. 3% - 2. 2%

Evaluation of ISO 9300 Tabulated C* Values Table B. 1: C* values for Methane 1 st Ed. 1990 2 nd Ed. 2005 ISO 9300 C* Tables (2005) • Range of Gas Types and Conditions P 0 = 8 MPa ISO Table R 8 NIST T 0 (K) * CISO * CR 8, NIST % Diff. 220 0. 99220 0% 240 0. 83585 0% 230 0. 91403 0. 89018 2. 7 % Ø 7 Gas Types: (CO 2, Ar, N 2, Ar, CH 4, Air, Steam) Ø T 0 range: 200 K to 600 K • Interpolation Error ≈ 2. 7 % C* Uncertainty Ø P 0 range: up to 20 MPa • Limited gas types and P 0 and T 0 range • Uncertainty of C* = 0. 1 % (k = 2) Ø Generally good agreement with R 8 NIST Ø Interpolation Errors can be Significant • Not practical to Tabulate Mixtures Ø Wet Air Ø Natural Gas

Objectives 1) To suggest the use of REFPROP Thermodynamic Database for calculating C* 2) To introduce real gas corrections for large b = d/D applications 3) To present results experimentally from measuring C*

Real Gas Corrections for Large b = d/D > 0. 25 Tm P CFV (Critical Flow Venturi) D Flow d • CFV applications measure the recovery temp. (Tm) and the static pres. (P) • Stagnation conditions T 0 and P 0 are necessary to compute o Critical flow function; Cr*= Cr*(T 0, P 0) o Mass flow; & m= p d 2 P 0 M C *Cd 4 Ru T 0 • Stagnation conditions are based on 1) Ideal gas or 2) Polytropic gas o Ideal Gas; o Polytropic Gas; & & Large errors can result for b > 0. 25 when real gas effects are significant

How do you compute P 0 and T 0 for large b ? Required Inputs 1) Diameter ratio: b = d/D 2) Measured Temperature: Tm 3) Measured Pressure: P 1 D Steady Navier-Stokes Flow Model 1) Isentropic Flow: s(T 0, P 0) = s(T *, P*) 2) Isoenergetic Flow: h(T 0, P 0) = h(T *, P*) + a(T *, P*)2/2 3) Isentropic Flow: s(T 0, P 0) = s(T , P) 4) Isoenergetic Flow: h(T 0, P 0) = h(T , P) + u 2/2 5) Mass Conservation: r(T*, P*)a(T*, P*)b 2 = r(T, P)u 6) Recovery Factor (RF): RF = (Tm – T )/ (T 0 – T )

Evaluation of Ideal and Polytropic Gas Models Comparison Parameters 1)% Difference T 0 2)% Difference P 0 3)% Difference C* 4)% Difference (Theoretical Mass Flux) % Diff x Example: % Diff T 0

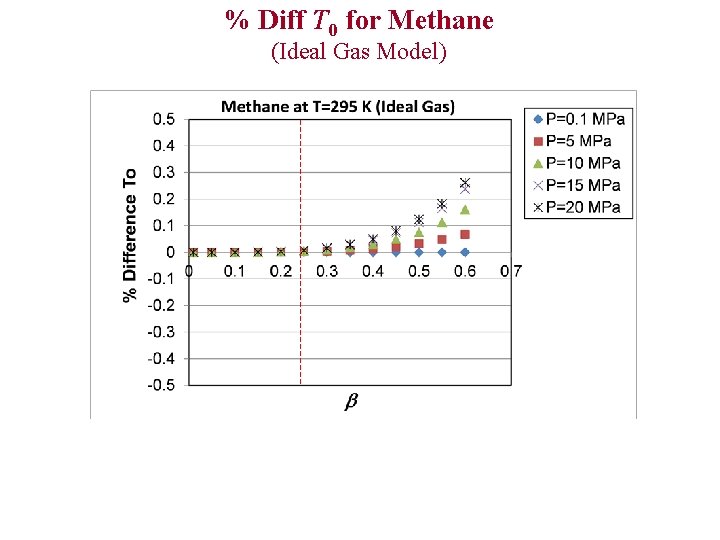
% Diff T 0 for Methane (Ideal Gas Model)

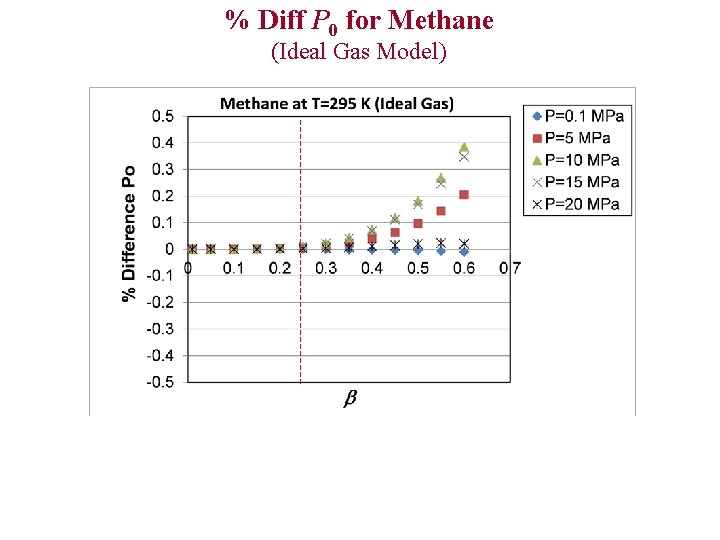
% Diff P 0 for Methane (Ideal Gas Model)

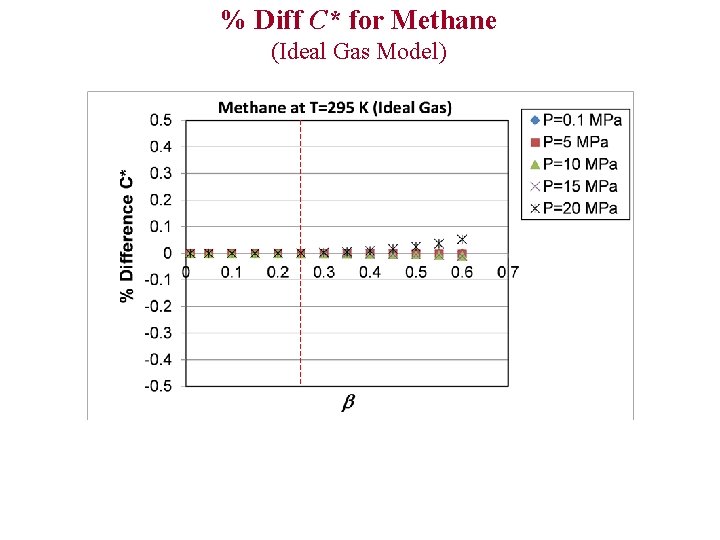
% Diff C* for Methane (Ideal Gas Model)

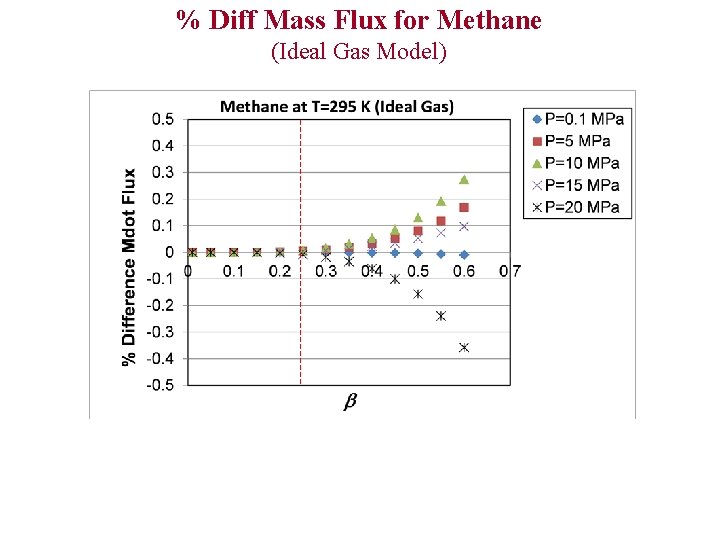
% Diff Mass Flux for Methane (Ideal Gas Model)

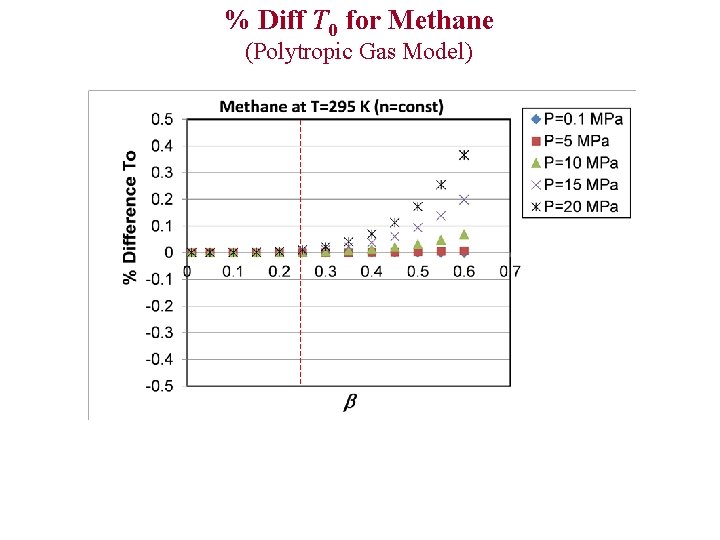
% Diff T 0 for Methane (Polytropic Gas Model)

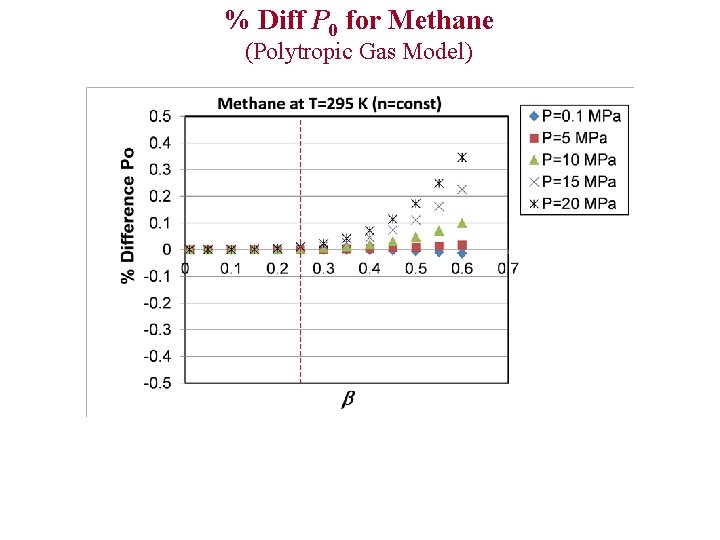
% Diff P 0 for Methane (Polytropic Gas Model)

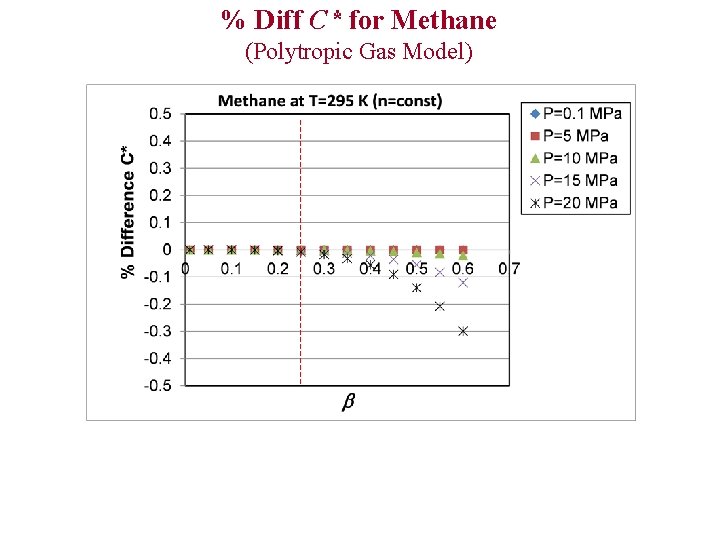
% Diff C* for Methane (Polytropic Gas Model)

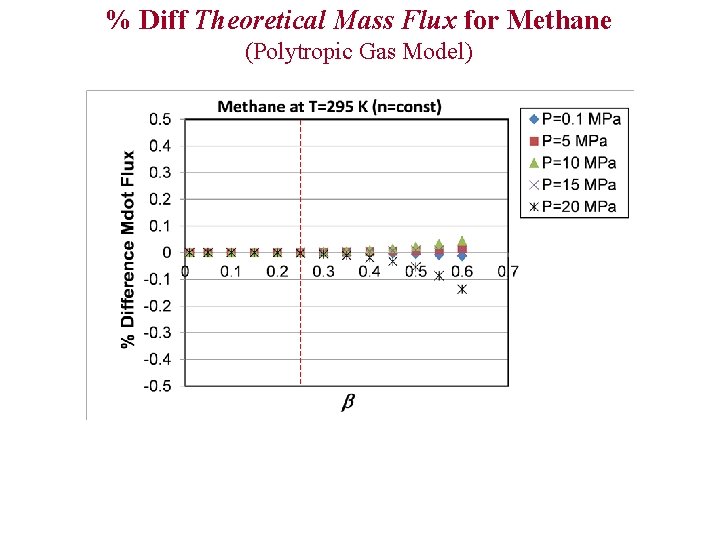
% Diff Theoretical Mass Flux for Methane (Polytropic Gas Model)

Objectives 1) To suggest the use of REFPROP Thermodynamic Database for calculating C* 2) To introduce real gas corrections for large b = d/D applications 3) To present results experimentally from measuring C*

A Technique for Measuring C*R • Measure CFV mass flow with low uncertainty standard in gas A o Gas A is selected so that it behaves closely to ideal gas o C* can be calculated by REFPROP at low uncertainty • Measure CFV mass flow with low uncertainty standard in gas B at the same Reynolds number: o Gas B has significant real gas effects • Determine CB* using the following expression:

A Technique for Measuring C*R (Cont) Advantages • No geometric dependence o it can be applied to small CFVs at high pressures o Analytical CFV theory can be used to estimated d • Cd Ratio approaches unity at high Reynolds numbers • All of the dependents can be measured at low uncertainty Requirement • Low uncertainty primary standard capable of measuring multiple gas compositions

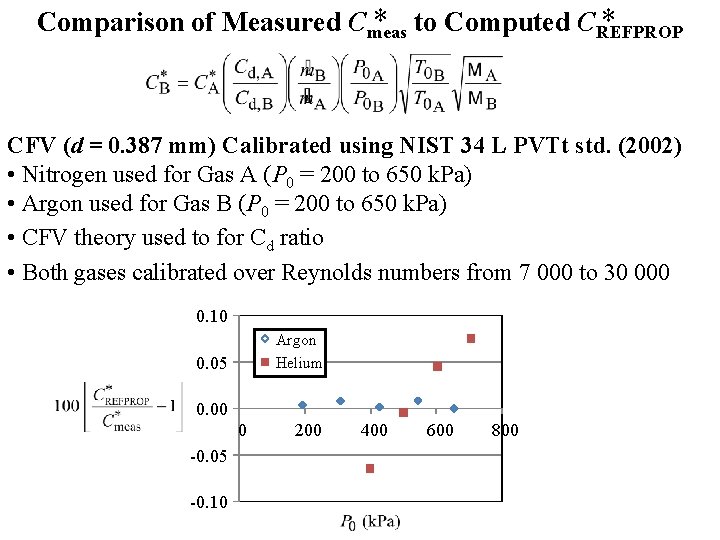
* to Computed CREFPROP * Comparison of Measured Cmeas CFV (d = 0. 387 mm) Calibrated using NIST 34 L PVTt std. (2002) • Nitrogen used for Gas A (P 0 = 200 to 650 k. Pa) • Argon used for Gas B (P 0 = 200 to 650 k. Pa) • CFV theory used to for Cd ratio • Both gases calibrated over Reynolds numbers from 7 000 to 30 000 0. 10 Argon Helium 0. 05 0. 00 0 -0. 05 -0. 10 200 400 600 800

Some Disccussion Topics 1) How are you currently computing C*? 2) Does it make sense to standardize the software used to compute C*? 3) The ISO 9300 includes a multi-parameter curve fit for select gases to correct the CFV mass flux for large b. Would it be useful to have REFPROP make these corrects? 4) Other questions and points of dissusion