The Cosine Rule C b a A B

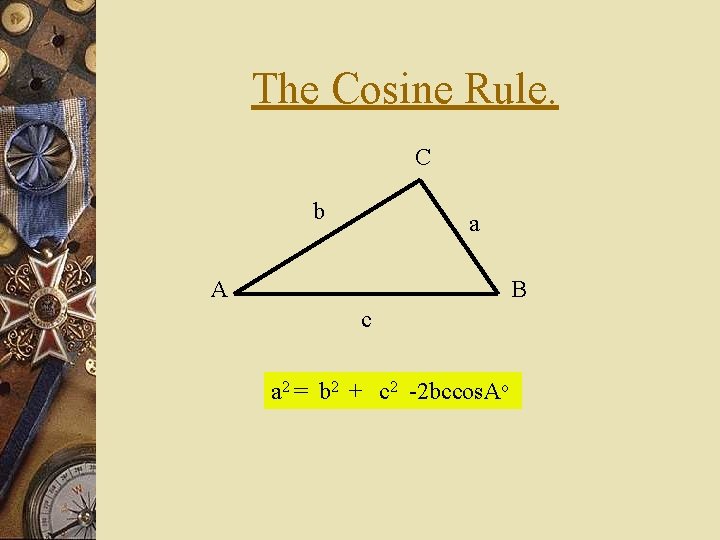
The Cosine Rule. C b a A B c a 2 = b 2 + c 2 -2 bccos. Ao

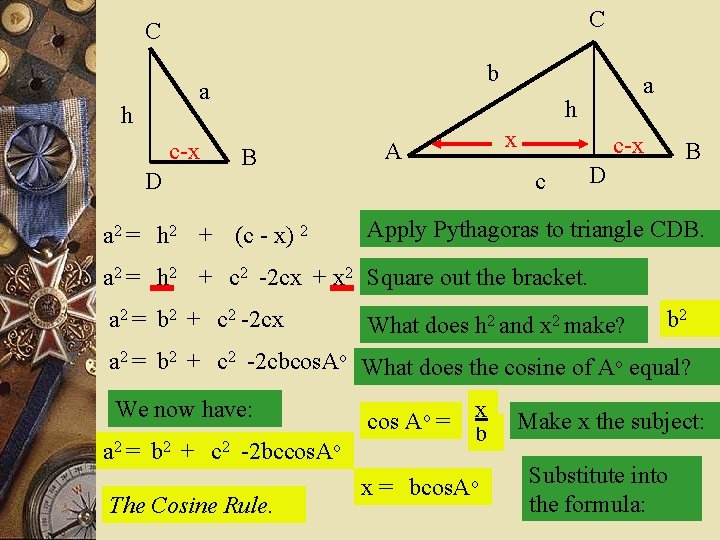
C C b a h c-x D a h B a 2 = h 2 + (c - x) 2 x A c-x c B D Apply Pythagoras to triangle CDB. a 2 = h 2 + c 2 -2 cx + x 2 Square out the bracket. a 2 = b 2 + c 2 -2 cx What does h 2 and x 2 make? b 2 a 2 = b 2 + c 2 -2 cbcos. Ao What does the cosine of Ao equal? We now have: a 2 = b 2 + c 2 -2 bccos. Ao The Cosine Rule. cos Ao = x b x = bcos. Ao Make x the subject: Substitute into the formula:

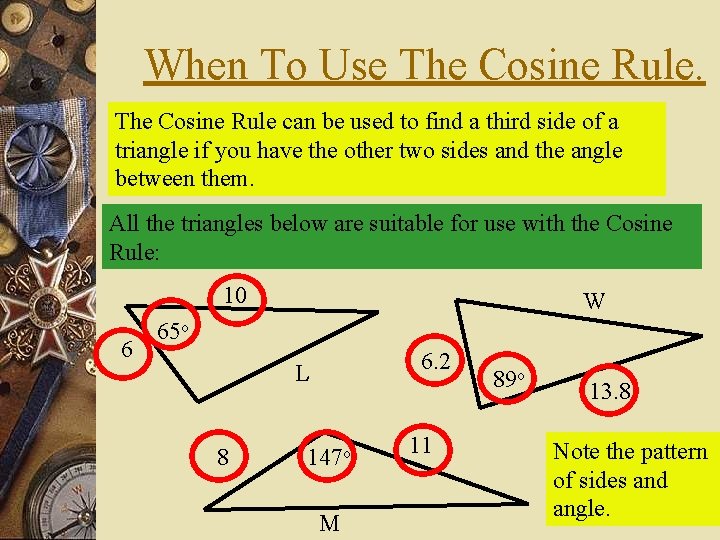
When To Use The Cosine Rule can be used to find a third side of a triangle if you have the other two sides and the angle between them. All the triangles below are suitable for use with the Cosine Rule: 10 6 W 65 o 6. 2 L 8 147 o M 11 89 o 13. 8 Note the pattern of sides and angle.

Using The Cosine Rule. Example 1. Find the unknown side in the triangle below: L 5 m Identify sides a, b, c and angle Ao 43 o 12 m a= L b= 5 Write down the Cosine Rule. c =12 a 2 = b 2 + c 2 -2 bccos. Ao Ao = 43 o Substitute values and find a 2 = 52 + 122 - 2 x 5 x 12 cos 43 o a 2 = 25 + 144 - (120 x 0. 731 ) a 2 = 81. 28 Square root to find “a”. a = 9. 02 m

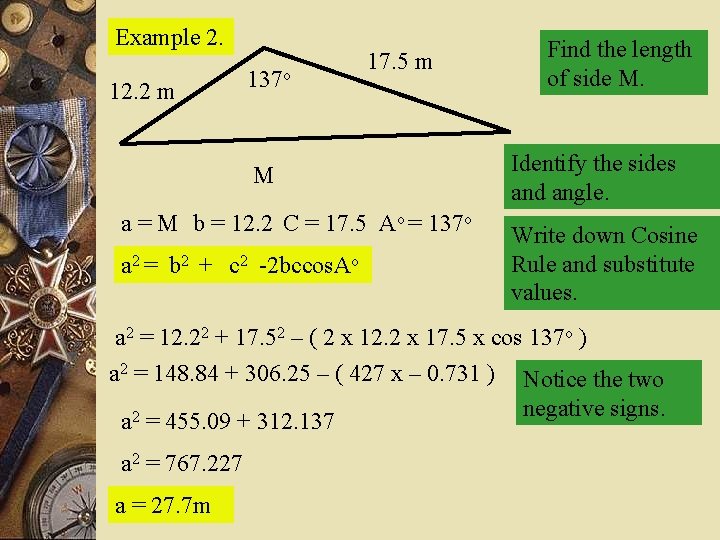
Example 2. 12. 2 m 137 o 17. 5 m M a = M b = 12. 2 C = 17. 5 Ao = 137 o a 2 = b 2 + c 2 -2 bccos. Ao Find the length of side M. Identify the sides and angle. Write down Cosine Rule and substitute values. a 2 = 12. 22 + 17. 52 – ( 2 x 12. 2 x 17. 5 x cos 137 o ) a 2 = 148. 84 + 306. 25 – ( 427 x – 0. 731 ) Notice the two negative signs. 2 a = 455. 09 + 312. 137 a 2 = 767. 227 a = 27. 7 m

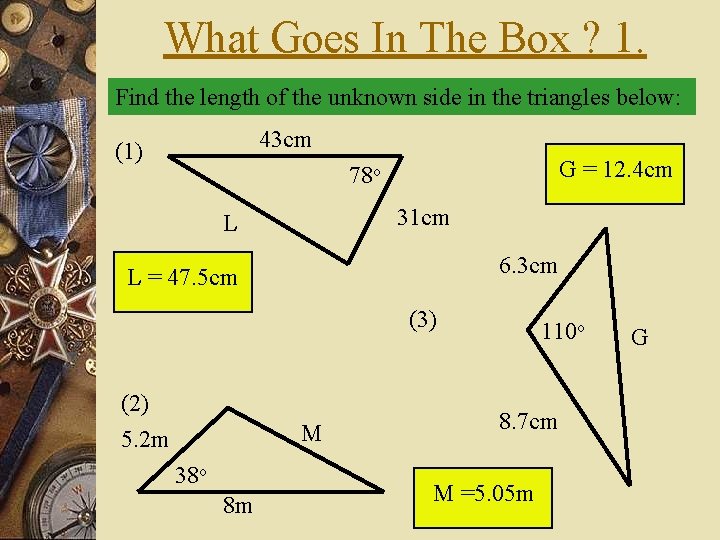
What Goes In The Box ? 1. Find the length of the unknown side in the triangles below: 43 cm (1) G = 12. 4 cm 78 o 31 cm L 6. 3 cm L = 47. 5 cm (3) (2) 5. 2 m M 38 o 8 m 110 o 8. 7 cm M =5. 05 m G

Finding Angles Using The Cosine Rule. Consider the Cosine Rule again: a 2 = b 2 + c 2 -2 bccos. Ao We are going to change the subject of the formula to cos Ao b 2 + c 2 – 2 bc cos Ao = a 2 Turn the formula around: -2 bc cos Ao = a 2 – b 2 – c 2 Take b 2 and c 2 across. Divide by – 2 bc. Divide top and bottom by -1 You now have a formula for finding an angle if you know all three sides of the triangle.

Example 1 Finding An Angle. Use the formula for Cos Ao to calculate the unknown angle xo below: 9 cm Ao = x o a = 11 b = 9 c = 16 11 cm xo 16 cm Write down the formula for cos Ao Identify Ao and a , b and c. Cos Ao = 0. 75 Substitute values into the formula. Ao Calculate cos Ao. = 41. 4 o Use cos-1 0. 75 to find Ao

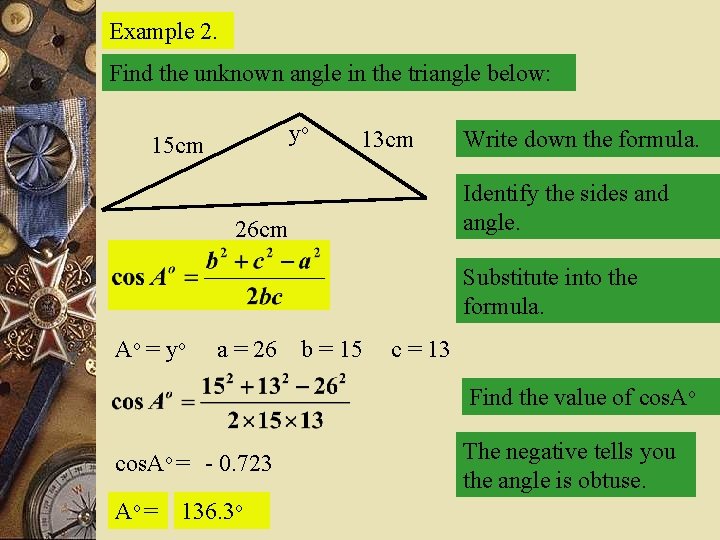
Example 2. Find the unknown angle in the triangle below: yo 15 cm 13 cm Write down the formula. Identify the sides and angle. 26 cm Substitute into the formula. Ao = yo a = 26 b = 15 c = 13 Find the value of cos. Ao = - 0. 723 Ao = 136. 3 o The negative tells you the angle is obtuse.

What Goes In The Box ? 2 Calculate the unknown angles in the triangles below: (1) 5 m ao 7 m (3) ao =111. 8 o 10 m 27 cm 12. 7 cm (2) 14 cm co 16 cm bo 7. 9 cm bo = 37. 3 o 8. 3 cm co =128. 2 o