The Copernican Cosmos Ptolemaic Universe Epicycles Upon Epicycles

The Copernican Cosmos

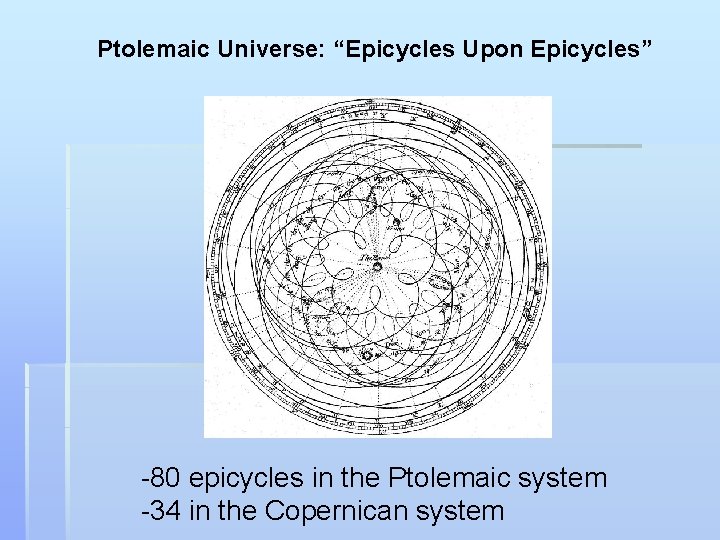
Ptolemaic Universe: “Epicycles Upon Epicycles” -80 epicycles in the Ptolemaic system -34 in the Copernican system

Copernicus: § Application of Occam’s razor? Yes. Epicycles overpopulate the heavens. Overly complex system.

Three incorrect assumptions § § § Earth was the center of the universe Uniform circular motion in the heavens Planets made from a perfect, unchanging substance not found on the Earth (quintessence).

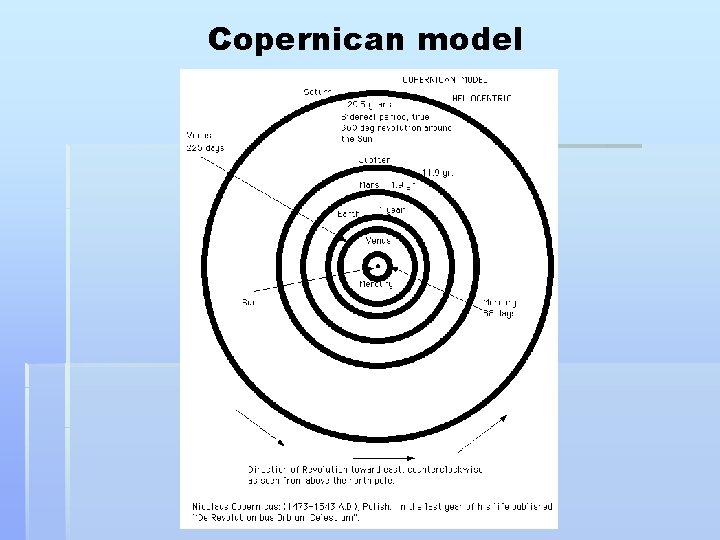
Copernican Revolution § Copernican Revolution is a term which applies to the transition from a geocentric cosmological model to a heliocentric model.

Copernican model

Tycho and Stellar Parallaxes § Bio (1546 -1601) -scientist (astronomer) -the nose

Sextant

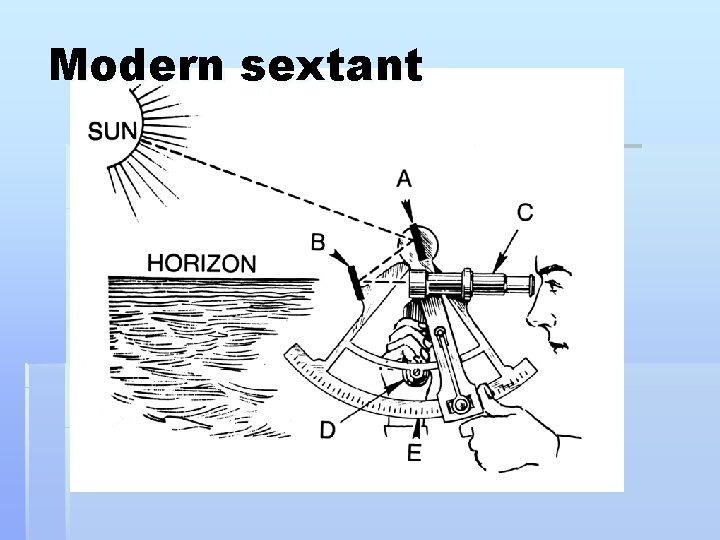
Sextant -measures the angles between two objects, generally a celestial object and the horizon

Modern sextant

Why is the sextant important to science? �Brahe used them for stellar measurements �Better navigation for ships �Observation of a stellar parallax for Tycho? No, a parallax is not observed until 1838 with the help of a strong telescope.

Parallax § Illustration

Tycho’s Cosmological Model

Tycho’s Cosmological Model § Tried to reconcile Ptolemaic and Copernican systems the five planets orbit the Sun, while the Moon and the Sun orbit the stationary Earth. Sphere of fixed stars remained. Brahe supported his model by observing that the stars did not shift (i. e. , he could not observe parallaxes).

Other Contributions to Science § Studies on the new star of 1572 § Studies on comet of 1574 Both challenge the veracity of the Aristotelian contention that the heavens are inalternable, incorruptible.

Tycho’s cosmology merges the Ptolemaic and Copernican systems. Geocentric universe with the planets revolving around the sun. Why? He could not observe a stellar parallax (shifting of the stars) which would involve great distances of empty space which was an implausible notion (horror vacui-nature abhors a vacuum). Made and used a sextant for stellar measurements. Sextant has practical uses for seafaring. Discovery of star (nova) of 1572 and comet of 1574 turns Aristotle’s thesis of the inalterability of the heavens on its head.

§ Assumption of uniform circular motion (planetary circular orbits).

Johannes Kepler 1571 -1630

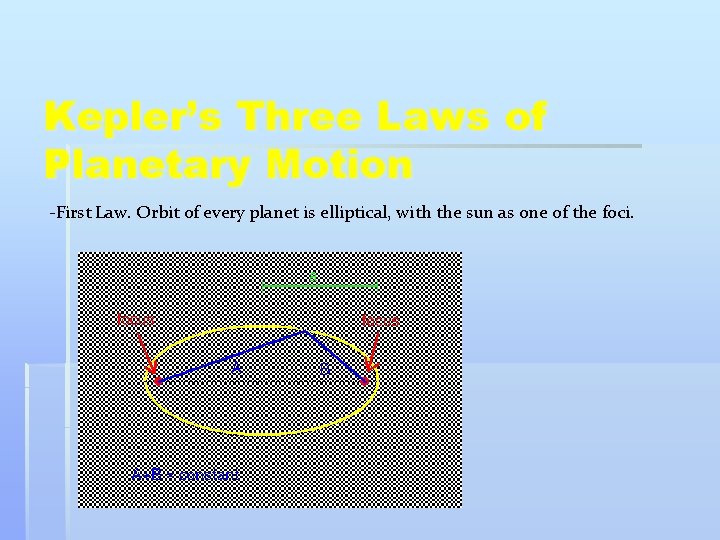
Kepler’s Three Laws of Planetary Motion -First Law. Orbit of every planet is elliptical, with the sun as one of the foci.

Kepler’s Three Laws of Planetary Motion -Second Law. The radius vector (of a planet) traverses equal areas in equal times.

Kepler’s Three Laws of Planetary Motion -Third Law. T 2 = R 3 the square of the time of one orbital period (T 2) is equal to the cube of its average orbital radius (R 3). Problem: What is Venus’s average distance from the sun? Well, we know Venus takes 224. 7 earth days to orbit the sun. Venus’s orbital period then would be 224. 7/365 or. 61 earth years. Since T 2 = R 3, then. 612=R 3 or. 3721= R 3 3√. 3721 = 3√ R 3 . 71926=R Which would be. 71926 AU (astronomical units). If one AU for earth is 93, 000 miles, then Venus’s average distance would be 66, 859, 484. 352618 miles.

Next time, class presentation