The Concept of the Bernoulli Distribution Volume 2

The Concept of the Bernoulli Distribution Volume 2 Chapter 12

Consider the random experiments and their possible outcomes below: Either heads or tails shows up when a coin is tossed; the sex of a baby to be born is either male or female. Can you point out the common characteristic of these two events? Both of them have only two possible outcomes. Volume 2 Chapter 12

Random experiments which result in only two possible outcomes are called Bernoulli trials. Note that the two outcomes must be complementary. Volume 2 Chapter 12

For convenience, we describe one of the two possible outcomes as a ‘success’ and the other a ‘failure’. Note: 1. A ‘success’ does not necessarily represent a good or a desirable outcome but the outcome we are concerned about. 2. For random experiments with more than two outcomes, we may still regard them as Bernoulli trials by considering certain outcomes as ‘success’ and all the other outcomes as ‘failure’. Volume 2 Chapter 12

If X is a random variable involved in a Bernoulli trial, such that then X is called a Bernoulli variable. The probability distribution of X, called Bernoulli distribution, is given by where p is the probability of ‘success’ and 1 – p is the probability of ‘failure’ and 0 < p < 1. Volume 2 Chapter 12

We can use a probability function to represent the Bernoulli distribution. Note that the actual values of P(X = 0) and P(X = 1) can only be found by knowing the value of p. p is called the parameter of the Bernoulli distribution. The mean (or expectation) and the variance of a Bernoulli distribution are as follows: Volume 2 Chapter 12

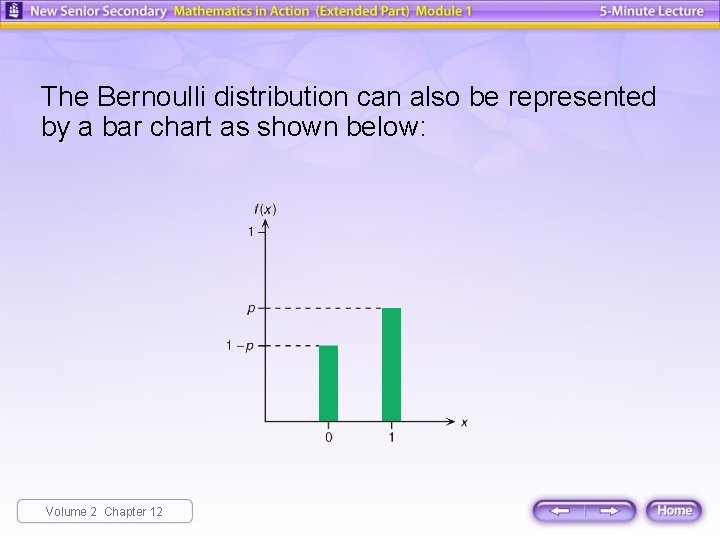
The Bernoulli distribution can also be represented by a bar chart as shown below: Volume 2 Chapter 12

Here are some examples of Bernoulli variables X. Experiment (Trial) Success Failure p X Toss a coin once Heads Tails 0. 5 0 or 1 Give birth to child Boy Girl 0. 5 0 or 1 Throw a dice once ‘ 6’ ‘ 1’, ‘ 2’, ‘ 3’, ‘ 4’, ‘ 5’ Volume 2 Chapter 12 0 or 1

Follow-up question The probability function of a Bernoulli distribution is Find (a) (b) the value of p, the mean and the variance of X. Solution (a) ∵ ∴ Volume 2 Chapter 12

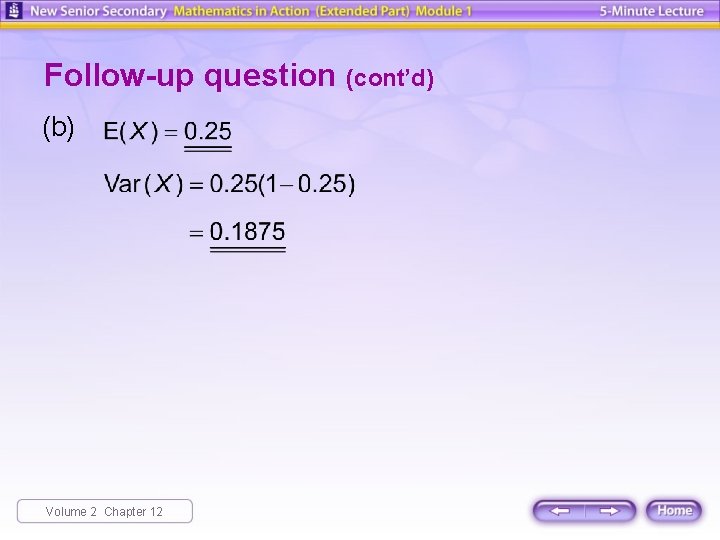
Follow-up question (cont’d) (b) Volume 2 Chapter 12