The Compton Effect 1923 Compton scattered shortwavelength light

The Compton Effect (1923) Ü Compton scattered short-wavelength light (X-rays) from different materials Ü The scattered light had lower frequency than the incident light Ü Meaning there was a loss of energy Ü The photon is a relativistic particle (moves at the speed of light) Ü λ 1 = λ + h/m 0 c (1 -cosΦ) Ü The Compton Wavelength h/m 0 c

The Compton Effect (1923) Ü Question: pg 834 Ü X-rays of wavelength 0. 140 nm are scattered from a block of carbon. What will be the wavelengths of Xrays scattered at Ü A) 0° Ü B) 90° Ü C) 180°

The Compton Effect Ü The Compton Effect has been used to diagnose bone disease such as osteoporosis Ü Radioactive gamma rays are scattered off bone material Ü The total intensity is proportional to the density of the scattered radiation, which is proportional to the bone density.

Wave-Particle Duality

Louis de Broglie (1892 -1987) Ü Extended the wave-particle duality theory Ü Thought that if light can sometimes behave like a wave and sometimes like a particle, then things thought to be particles might also behave like waves Ü Proposed that the wavelength of a material particle would be related to its momentum Ü λ= h/mv OR λ= h/p

Louis de Broglie (1892 -1987) ÜQuestion: pg 836 ÜCalculate the de Broglie wavelength of a 0. 2 kg ball moving with a speed of 15 m/s.

Louis de Broglie (1892 -1987) ÜThe wave properties of particles are only significant when the size of the object is not much larger than the wavelength.

Louis de Broglie (1892 -1987) ÜQuestion: pg 837 ÜDetermine the wavelength of an electron that has been accelerated through a potential difference of 100 V.

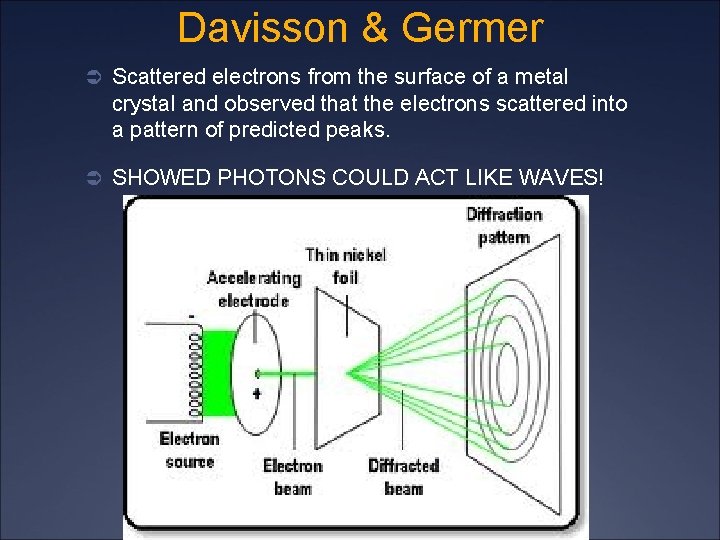
Davisson & Germer Ü Scattered electrons from the surface of a metal crystal and observed that the electrons scattered into a pattern of predicted peaks. Ü SHOWED PHOTONS COULD ACT LIKE WAVES!

Free Response Ü A photon of wavelength 250 nm ejects an electron from a metal. The ejected electron has a de Broglie wavelength of 0. 85 nm. Ü (a) Calculate the kinetic energy of the electron. Ü (b) Assuming that the kinetic energy found in (a) is the maximum kinetic energy that it could have, calculate the work function of the metal.

Atomic Energy Levels

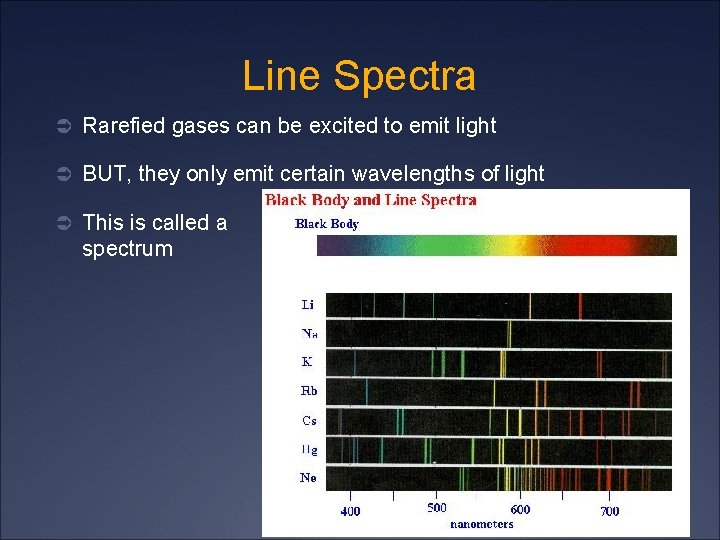
Line Spectra Ü Rarefied gases can be excited to emit light Ü BUT, they only emit certain wavelengths of light Ü This is called a spectrum line

Line Spectra Ü The emission spectrum is characteristic of the material and can be used to identify a gas Ü The emission spectrum is the same as the absorption spectrum Ü 1/λ = R(1/nf 2 – 1/ni 2) where R = 1. 097 x 107 m-1

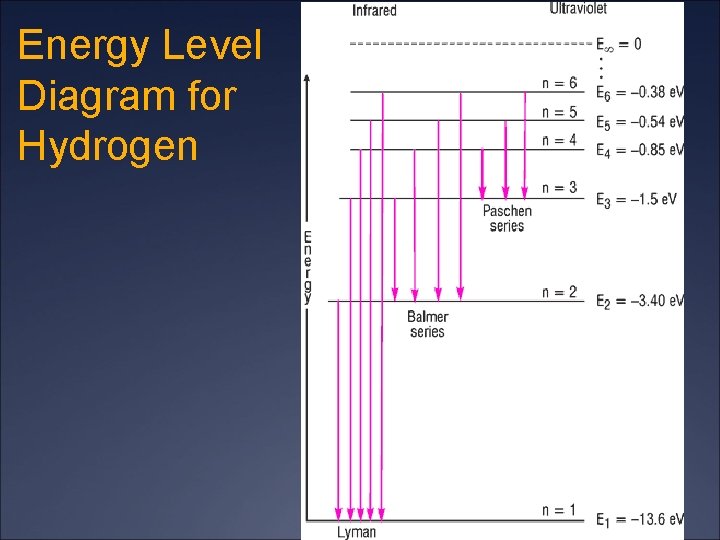
Energy Levels Ü Based on the discoveries of the Rydberg equation that not only do electrons absorb and emit energy in certain “packets” of energy, but they also orbit the nucleus in defined orbits Ü For atoms, the lowest energy level or energy state has the energy E 1 and is called the ground state Ü Any higher energy states are called excited states.

Energy Levels Ü The higher the energy level of an electron, the smaller the number Ü However, all energy is designated as negative Ü So even though numerically the number is smaller for larger orbits, the energy is actually greater

Energy Level Diagram for Hydrogen

Ionization Energy ÜAlso called ionization energy ÜThis is the minimum energy necessary to remove an electron from an atom

Wavelength Ü Question: pg 849 Ü Determine the wavelength of light emitted when a hydrogen atom makes a transition from n=6 to n=2 energy level according to the Bohr Model

Free Response Ü A photon of wavelength 250 nm ejects an electron from a metal. The ejected electron has a de Broglie wavelength of 0. 85 nm. Ü (a) Calculate the kinetic energy of the electron. Ü (b) Assuming that the kinetic energy found in (a) is the maximum kinetic energy that it could have, calculate the work function of the metal. Ü (c) The incident photon was created when an atom underwent an electronic transition. On the energy level diagram of the atom below, the transition labeled X corresponds to a photon wavelength of 400 nm. Indicate which transition could be the source of the original 250 nm photon by circling the correct letter.

Free Response Ü The electron energy levels above are for an electron confined to a certain very small one-dimensional region of space. The energy E of the levels, where n = 1, 2, 3, . . . , is given by E= n 2 E 1. Express all algebraic answers in terms of E 1 and fundamental constants. Ü (a) On the diagram above, label the three excited energy levels with the values for their energies in terms of E 1 , the energy of the ground state. Ü (b) Calculate the smallest frequency of light that can be absorbed by an electron in this system when it is in the ground state, n = 1.

Free Response Ü (c) If an electron is raised into the second excited state, draw on the diagram all the possible transitions that the electron can make in returning to the ground state. Ü (d) Calculate the wavelength of the highest energy photon that can be emitted in the transitions in part (c).

Free Response Practice Ü Following a nuclear reaction, a nucleus of carbon is at rest in an excited state represented by 126 C*. The excited nucleus returns to the ground state 126 C by emitting a gamma ray photon of energy 7. 65 Me. V. The carbon nucleus in the ground state has a mass of 2. 00852139 × 10 -26 kg. Assume non-relativistic equations apply to the motion of the nucleus. Ü A) Calculate the wavelength of the emitted photon in meters. Ü B) Calculate the momentum of the emitted photon in kg*m/s. Ü C) Calculate the speed of the recoiling nucleus in m/s. Ü D) Calculate the kinetic energy of the recoiling nucleus in joules.

Free Response Ü In an electron microscope, a titanium carbide cathode with work function 6. 82 e. V is heated to release electrons that are then initially at rest just outside the cathode. The electrons are accelerated by a potential difference to create a beam of electrons with a de Broglie wavelength of 0. 097 nm. Assume non-relativistic equations apply to the motion of the electrons. Ü 1) Calculate the momentum of an electron in the beam, in kg*m/s. Ü 2) Calculate the kinetic energy of an electron in the beam, in joules. Ü 3) Suppose that light, instead of heat, is used to release the electrons from the cathode. What minimum frequency of light is needed to accomplish this?

Nuclear Physics

Terms Ü Nucleon: a subatomic particle that resides in the nucleus Ü Atomic Number: the number of protons in an atom Ü Atomic Mass Number: the number of neutrons + protons

Binding Energy Ü The total mass of a stable nucleus is always less than the sum of the masses of its constituent protons and neutrons Ü Ex. Pg 919 Ü Compare the mass of a constituent nucleons 4 2 He nucleus to that of its Ü 2 mn = 2. 017330 amu Ü 2 m (11 H) = 2. 105650 amu 4. 032980 amu Ü The difference in mass is called the binding energy

Binding Energy ÜCalculate the total binding energy and the average binding energy per nucleon for 5626 Fe, the most common stable isotope of iron. Ü 931. 5 Me. V/amu

Strong Nuclear Force Ü A force that acts between all nucleons in an atom Ü A precise mathematical description is not yet possible Ü It acts over an extremely short distance Ü Less than 10 -15 m Ü The electromagnetic and gravitational forces can act over much longer distances Ü There are no stable nuclei over Z=82

Alpha Decay Ü Represented by α Ü When a helium nucleus is given off (42 He) Ü This is the HEAVIEST decay particle by far Ü Example Ü 226 88 Ra 22286 Rn + 42 He

Alpha Decay Ü Calculate the disintegration energy when 23292 U (mass = 232. 037131 amu) decays to 22890 Th (mass= 228. 028716 amu) with the emission of an α particle. Ü Mass of α particle: 4. 002602 amu Ü 1 amu = 931. 5 Me. V

Beta Decay Ü β- : Beta negative decay Ü A Z N AN+1 N 1 + e- + anti-neutrino Ü β+ : Beta positron decay Ü A Z N AN-1 N 1 + e+ + neutrino

Gamma Ray Decay ÜThe emission of high energy particles ÜThe gamma particle, γ , is weightless and neutral ÜA A N + γ N* Z Z