The circumference and Area of a circle Circles

The circumference and Area of a circle

Circles • A circle is the set of all points in a plane that are the same distance from a given point, called the center.

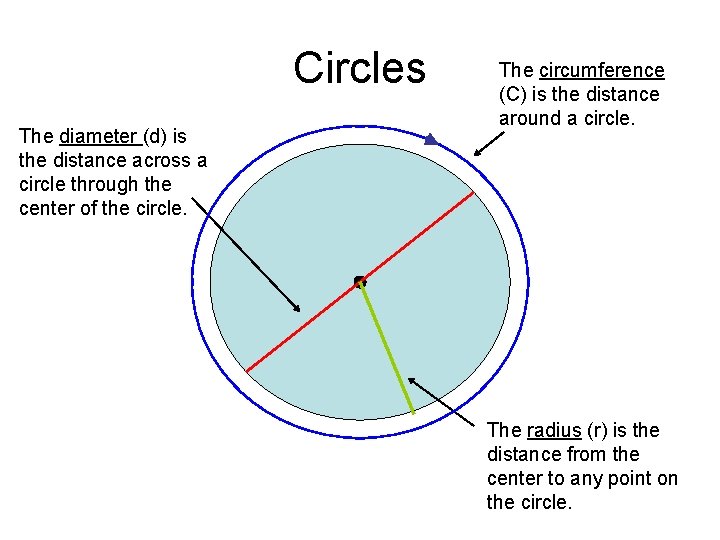
Circles The diameter (d) is the distance across a circle through the center of the circle. The circumference (C) is the distance around a circle. The radius (r) is the distance from the center to any point on the circle.

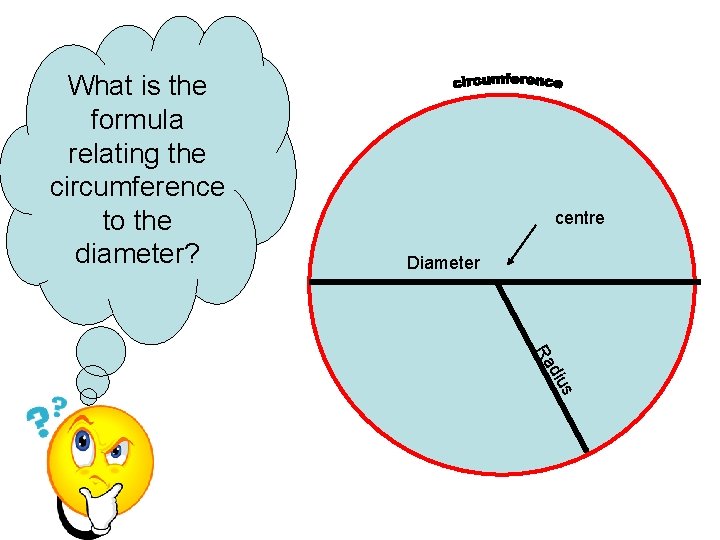
What is the formula relating the circumference to the diameter? centre Diameter ius d Ra

C=? xd People knew that the circumference is about 3 times the diameter but they wanted to find out exactly. C≈3 xd This means APPROXIMATELY EQUAL TO

The exact true value is…………… UNKNOWN!!

An approximation to π π≈3. 141592653589793238462643383279502884 19716939937510582097494459230781640628 62089986280348253421170679821480865132 82306647093844609550582231725359408128 48111745028410270193852110555964462294 89549303819644288109756659334461284756 48233786783165271201909145648566923460 34861045432664821339360726024914127372 45870066063155881748815209209628292540 91715364367892590360011330530548820466 521384146951941511609. . . . forever….

The Area and Perimeter of a Circle rad ius A circle is defined by its diameter or radius The perimeter or circumference of a circle is the distance around the outside The area of a circle is the space inside it Diameter The ratio of π (pi) π is an irrational number whose value to 15 decimal places is π = 3. 14159265358979. . The circumference is found using the formula C=π d or C= 2πr (since d=2 r) We usually say π≈3. 14 The area is found using the formula A=πr 2

The Area and Perimeter of a Circle rad ius A circle is defined by its diameter or radius The perimeter or circumference of a circle is the distance around the outside The area of a circle is the space inside it Diameter The ratio of π (pi) π is an irrational number whose value to 15 decimal places is π = 3. 14159265358979. . The circumference is found using the formula C=π d or C= 2πr (since d=2 r) We usually say π≈3. 14 The area is found using the formula A=πr 2

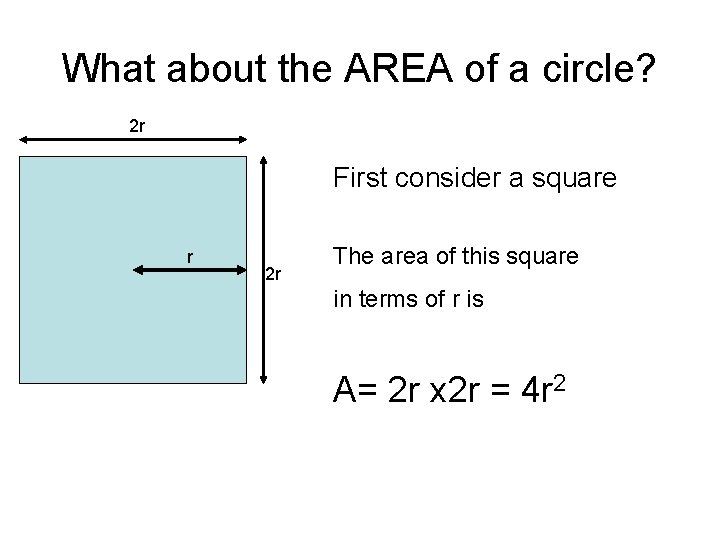
What about the AREA of a circle? 2 r First consider a square r 2 r The area of this square in terms of r is A= 2 r x 2 r = 4 r 2

What about the AREA of a circle? Now consider a circle inside the square 2 r The area of the circle must be less than the are of the square r 2 r A Area < 4 r 2 = ? xr 2

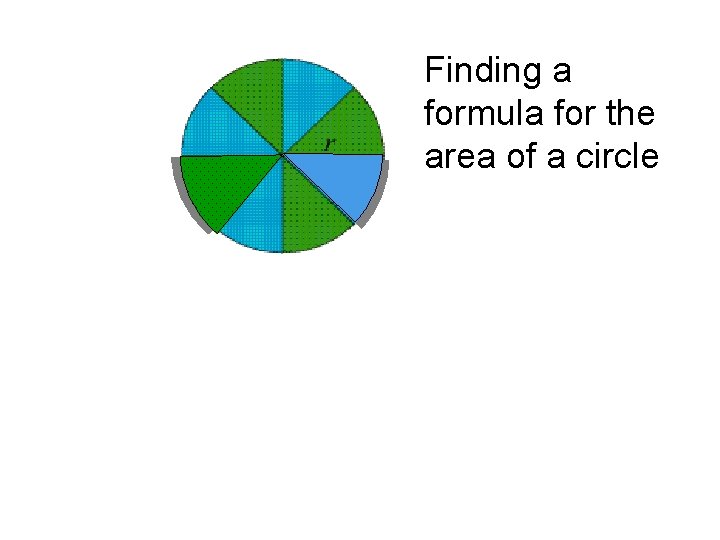
Finding a formula for the area of a circle

C= πd or C=2πr Semi-circle=πr πr r

Area of Rectangle= Base x Height Area = πr x r Area =πr 2