The Circle Introduction to circles Lets investigate Circumference

The Circle Introduction to circles Let’s investigate… Circumference examples Area of a circle Area examples

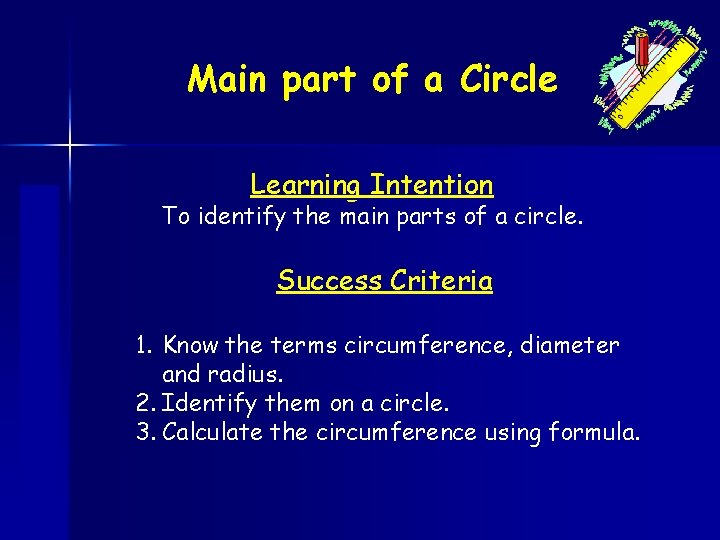
www. mathsrevision. com Main part of a Circle Learning Intention To identify the main parts of a circle. Success Criteria 1. Know the terms circumference, diameter and radius. 2. Identify them on a circle. 3. Calculate the circumference using formula.

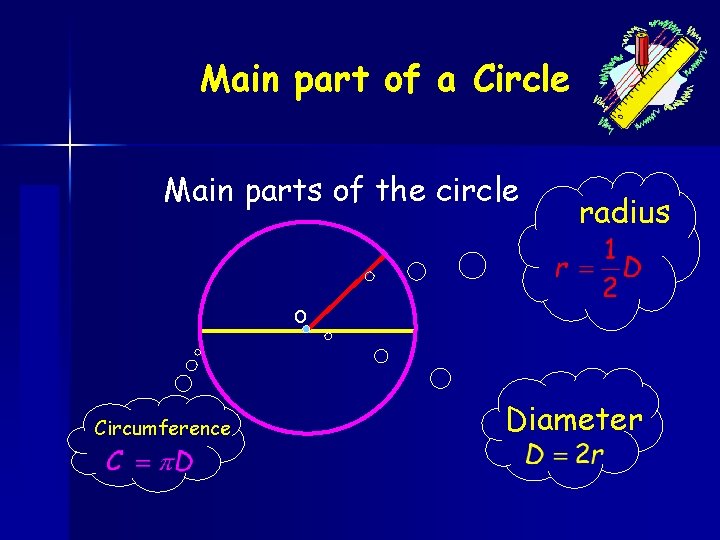
www. mathsrevision. com Main part of a Circle Main parts of the circle radius O Circumference Diameter

Let’s investigate… We can use a ruler to measure the diameter. How can we measure the circumference?

Let’s investigate… Work as a team at your table 1. Cut a piece of yarn that is exactly the length of the distance around the circular object at your table. (Called the circumference) 2. Cut another piece of yarn that is exactly the length of the distance through the middle of your circular object. (Called the diameter) 3. Use a ruler (in cm) to measure these two pieces of string. Be as accurate as possible! 4. Use a calculator to divide the Circumference by the diameter.

Let’s investigate… Look at the column circumference ÷ diameter is roughly 3. 14

Let’s investigate… circumference ÷ diameter is roughly 3. 14 There isn’t an exact answer for this. It actually goes on forever! In 1989 a computer worked it out to 480 million decimal places. 3. 141592653589793238462643383279502… We’ll stop here since it would stretch for 600 miles if we printed them all!

The Circumference If it goes on for ever how can I write it down? Mathematical Genius! We use the Greek letter instead. This is called pi.

The Circumference So circumference ÷ diameter = 3. 1415926535 By re-arranging this we get: Circumference = C= x diameter d

The Circumference When doing circle calculations, you will normally use a calculator. Some calculators have a button like this: This button stores to 8 or 9 decimal places which is more than accurate enough! 3. 141592654 If your calculator doesn’t have Then use 3. 14 instead.

Example 1 6 cm What is the circumference of this circle? C= d C= x 6 C = 18. 8 cm Press Then x 6=

Example 2 C= d d = 2 x 5 = 10 cm 5 cm What is the circumference of this circle? C= x 10 C = 31. 4 cm Remember: diameter = 2 x radius

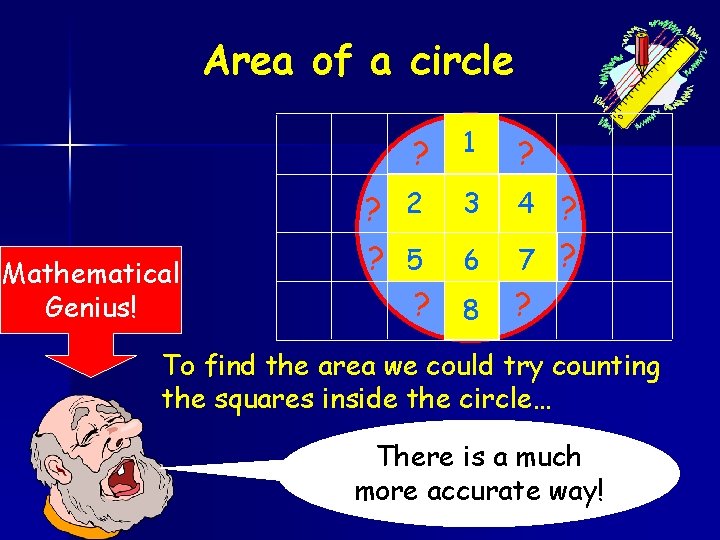
Area of a circle Mathematical Genius! ? 1 ? ? 2 3 4 ? ? 5 6 ? 8 7 ? ? To find the area we could try counting the squares inside the circle… There is a much more accurate way!

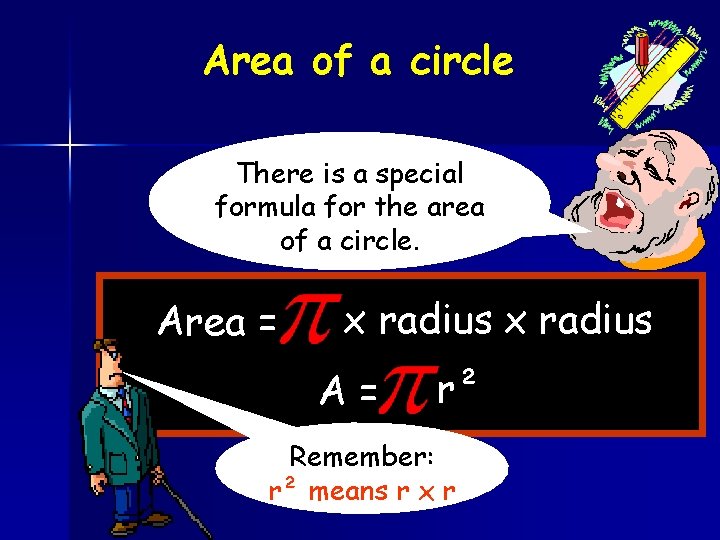
Area of a circle There is a special formula for the area of a circle. Area = x radius A= r² Remember: r² means r x r

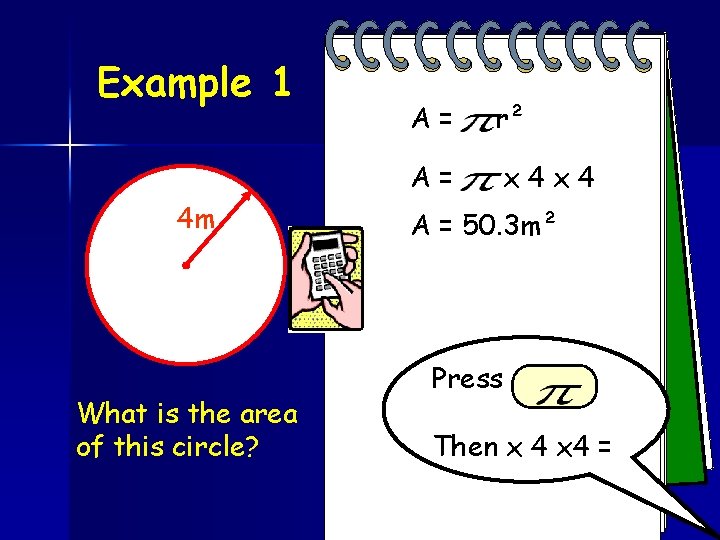
Example 1 4 m What is the area of this circle? A= r² A= x 4 x 4 A = 50. 3 m² Press Then x 4 =

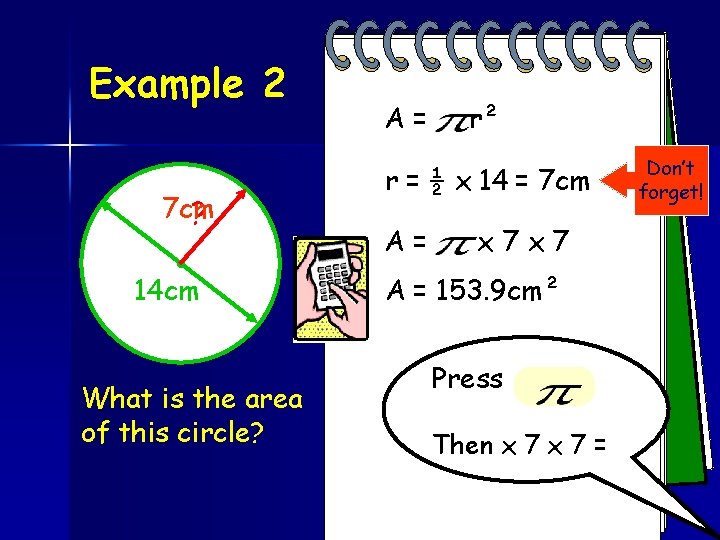
Example 2 7 cm ? 14 cm What is the area of this circle? A= r² r = ½ x 14 = 7 cm A= x 7 x 7 A = 153. 9 cm² Press Then x 7 = Don’t forget!

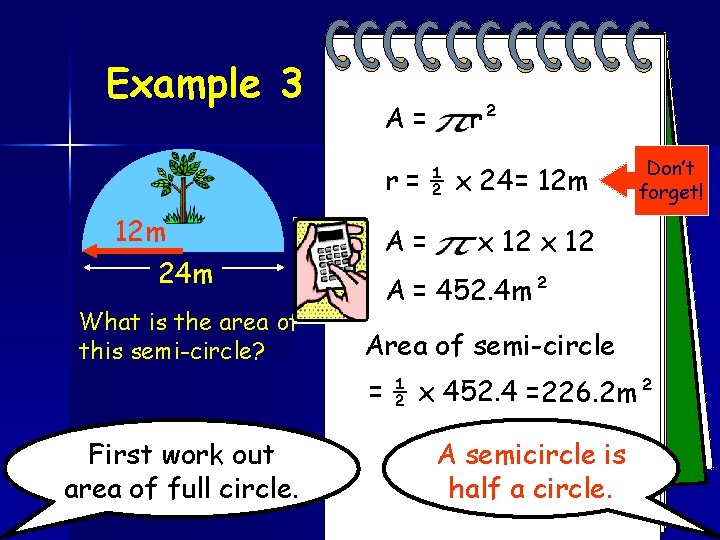
Example 3 A= r² r = ½ x 24 = 12 m ? 24 m What is the area of this semi-circle? A= Don’t forget! x 12 A = 452. 4 m² Area of semi-circle = ½ x 452. 4 =226. 2 m² First work out area of full circle. A semicircle is half a circle.

Joke of the Day! What do you get when you take the circumference of an apple and divide it by the diameter of the apple? Apple Pi!