The Chomsky Hierarchy 1 Unrestricted Grammars Rules have

The Chomsky Hierarchy 1

Unrestricted Grammars: Rules have form String of variables and terminals 2

Example grammar: 3

A language is generated by an unrestricted grammar if and only if is recursively enumerable 4

Context-Sensitive Grammars: Rules have form String of variables and terminals And: 5

The language is context-sensitive: 6

A language is context sensistive if and only if is accepted by a Linear-Bounded automaton 7

There is a language which is context-sensitive but not recursive 8

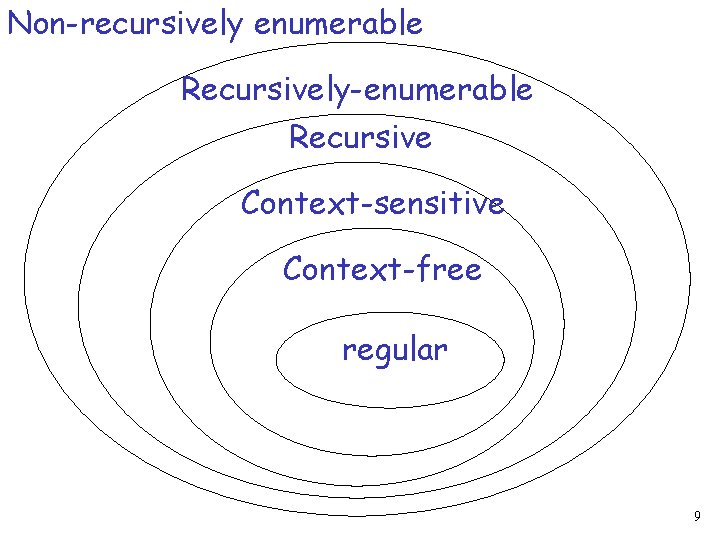
Non-recursively enumerable Recursively-enumerable Recursive Context-sensitive Context-free regular 9

Decidability 10

Consider problems with answer YES or NO Examples: • Does Machine • Is string • Does DFA have three states ? a binary number? accept any input? 11

A problem is decidable if some Turing machine solves the problem 12

Some decidable problems: • Does Machine • Is string • Does DFA have three states ? a binary number? accept any input? 13

The machine that decides the problem: • If the answer is YES then halts in a yes state • If the answer is NO then halts in a no state These states may not be final states 14

Difference between Recursive Languages and Decidable problems For decidable problems: The YES halting states may not be final states 15

There are some problems which are undecidable: There is no Turing Machine that solves all instances of the problem 16

A famous undecidable problem: The halting problem 17

The Halting Problem Inputs: • Turing Machine • String Question: Does halt on ? 18

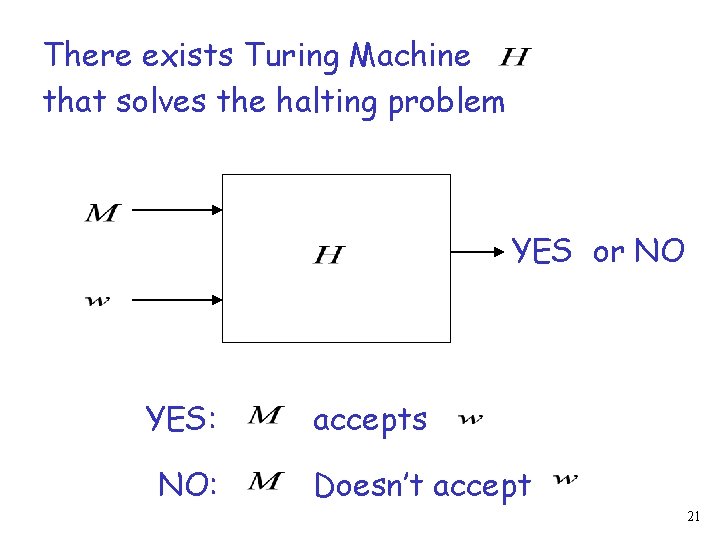
THEOREM The halting problem is undecidable 19

THEOREM The halting problem is undecidable PROOF Assume for contradiction that the halting problem is decidable 20

There exists Turing Machine that solves the halting problem YES or NO YES: NO: accepts Doesn’t accept 21

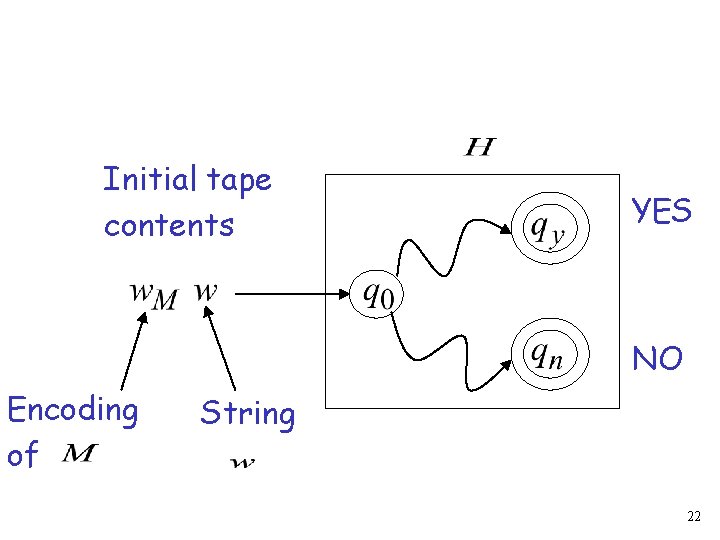
Initial tape contents YES NO Encoding of String 22

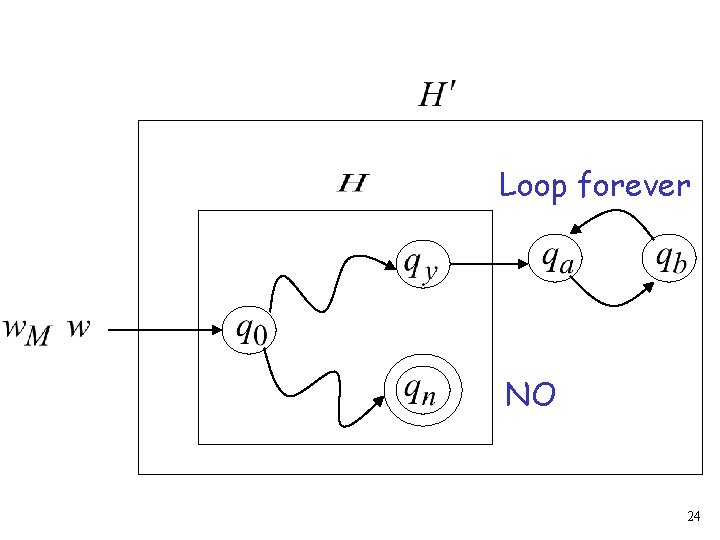
Construct machine : If returns YES then loop forever If returns NO then halt 23

Loop forever NO 24

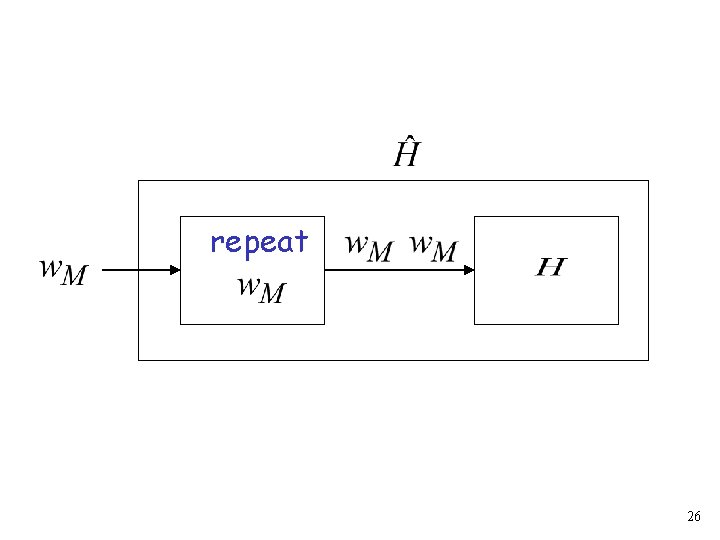
Construct machine Input: : (machine ) halts on input If then loop forever Else halt 25

repeat 26

Run machine with input itself 27

Run machine : Input: (machine ) halts on input If then loop forever Else halt 28

on input : If halts then loops forever If doesn’t halt then it halts NONSENSE !!!!! 29

Therefore, we have contradiction The halting problem is undecidable END OF PROOF 30

Another proof of the same theorem If the halting problem was decidable then every recursively enumerable language would be recursive 31

THEOREM The halting problem is undecidable PROOF Assume for contradiction that the halting problem is decidable 32

Turing Machine For inputs: solves the halting problem machine and string Returns: YES: if halts on input NO: if doesn’t halt on input 33

Let be a recursively enumerable language Let be the Machine that accepts We will prove that is recursive We will describe a membership algorithm 34

Run If with inputs: and Returns: NO: doesn’t halt on input Then doesn’t accept 35

If Returns: halts on input YES: Run with input will halt, and either accept or reject 36

Therefore is recursive But there are recursively enumerable languages which are not recursive Contradiction!!!! 37

Therefore, the halting problem is undecidable END OF PROOF 38

Reducibility 39

Problem is reduced to problem means If is decidable then is decidable 40

Problem is reduced to problem also means If is undecidable then is undecidable 41

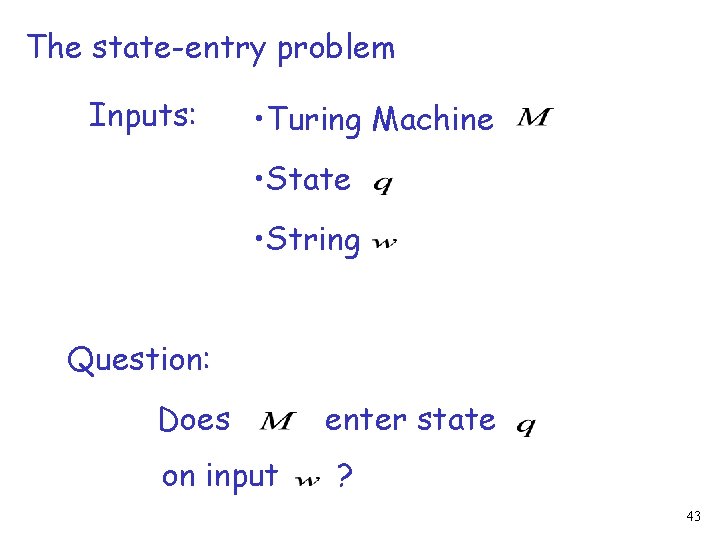
Example: The halting problem is reduced to The state-entry problem 42

The state-entry problem Inputs: • Turing Machine • State • String Question: Does on input enter state ? 43

THEOREM The state-entry problem is undecidable 44

THEOREM The state-entry problem is undecidable PROOF Reduce the halting problem to the state-entry problem 45

Suppose we have an algorithm for the state-entry problem We will construct an algorithm for the halting problem 46

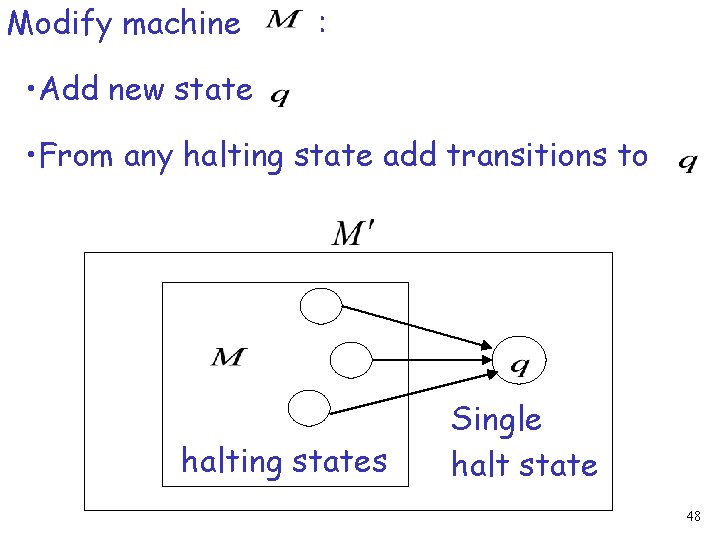
Inputs for the halting problem • A machine • A string Algorithm for halting problem must determine if halts on input 47

Modify machine : • Add new state • From any halting state add transitions to halting states Single halt state 48

halts if and only if halts on state 49

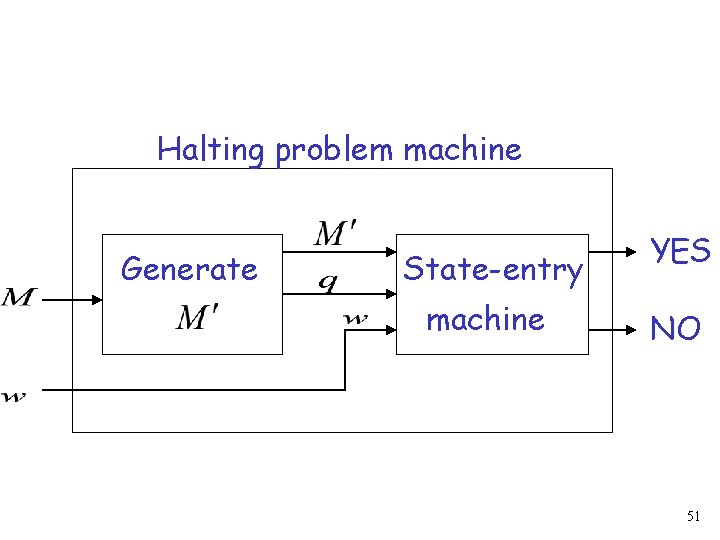
Algorithm for halting problem: Inputs: 1. Construct and with state 2. Run algorithm for state-entry problem , , with inputs: 50

Halting problem machine Generate State-entry machine YES NO 51

Since the halting problem is undecidable, the state-entry problem is also undecidable END OF PROOF 52

Another example: The halting problem is reduced to The blank-tape halting problem 53

The blank-tape halting problem Input: Turing Machine Question: Does halt when started with a blank tape? 54

THEOREM The blank-tape halting problem is undecidable 55

THEOREM The blank-tape halting problem is undecidable PROOF Reduce halting problem to Blank-tape halting problem 56

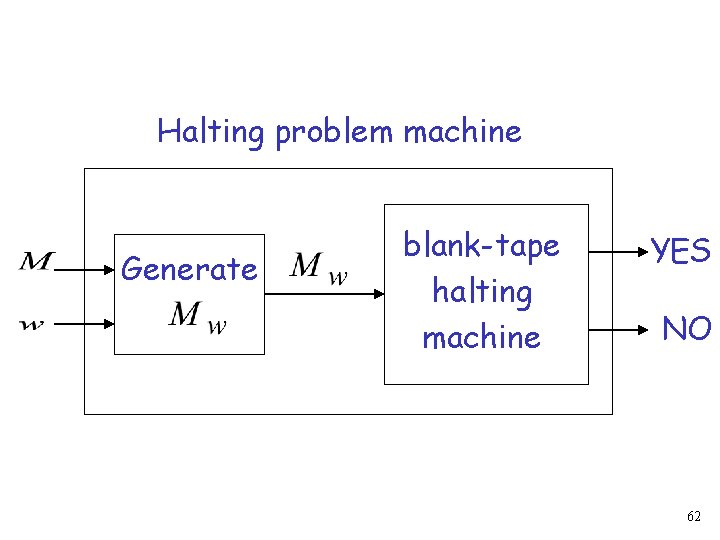
Suppose we have an algorithm for the blank-tape halting problem We will construct an algorithm for the halting problem 57

Inputs for the halting problem • A machine • A string Algorithm for halting problem must determine if halts on input 58

Construct a new machine • On blank tape writes • Then continues execution like 59

halts if and only if halts when started with blank tape 60

Algorithm for halting problem: Inputs: and 1. Construct 2. Run algorithm for , blank-tape halting, problem with input 61

Halting problem machine Generate blank-tape halting machine YES NO 62

Since the halting problem is undecidable, the blank-tape halting problem is also undecidable END OF PROOF 63