The Chinese University of Hong Kong Fall 2011

The Chinese University of Hong Kong Fall 2011 CSCI 3130: Formal languages and automata theory Limitations of pushdown automata Andrej Bogdanov http: //www. cse. cuhk. edu. hk/~andrejb/csc 3130

Non context-free languages L 1 = {anbn: n ≥ 0} ✔ L 2 = {s: s has same number of as and bs} ✔ L 3 = {anbncn: n ≥ 0} ? L 4 = {ss. R: s {a, b}*} L 5 = {ss: s {a, b}*} These are not regular Are they context-free?

An attempt L 3 = {anbncn: n ≥ 0} • Let’s try to design a CFG or PDA S → a. Bc | e B → ? ? read a / push x read b / pop x ? ? ?

What would happen if. . . • Suppose we could construct some CFG for L 3, e. g. S BC B CS | b C SB | a. . . • Let’s do some long derivations S BC CSC a. BCC aba. SB aba. BCB ababa. B ababab

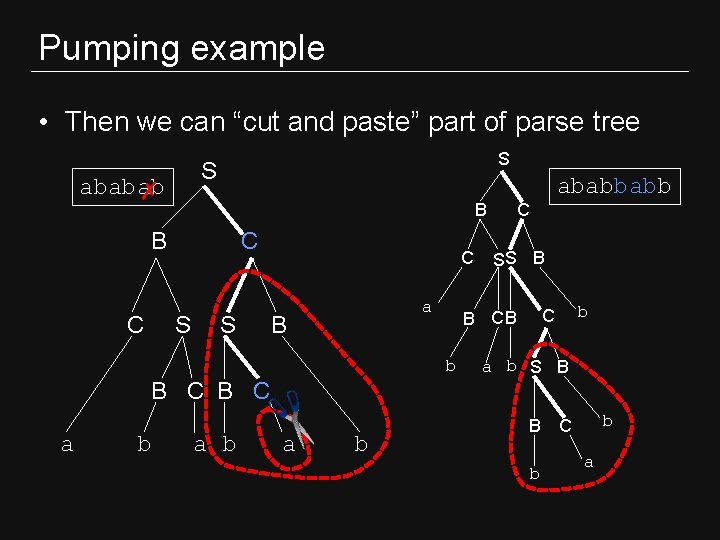
Repetition in long derivations • If derivation is long enough, some variable must appear twice on same path in parse tree S BC CSC a. BCC aba. SB aba. BCB ababa. B ababab S B C C S S B B C a b a b

Pumping example • Then we can “cut and paste” part of parse tree S S ababab ✗ C C B B C S S C a B SS B b C B CB b ababbabb a b S B B C a b a b B b b C a

Pumping example • We can repeat this many times ababab ✗ ababbabb ✗ ababbb ababnabnbb • Every sufficiently large derivation will have a middle part that can be repeated indefinitely

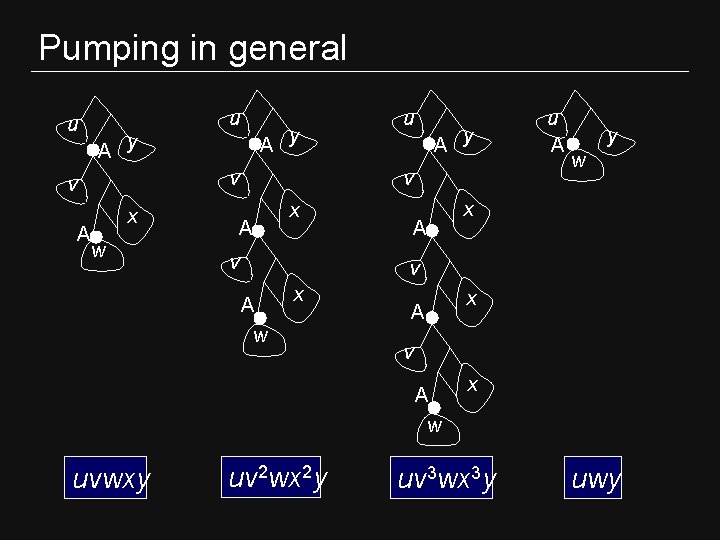
Pumping in general u u x w A y v v v A A y u x A v u A y w x A v A x w uvwxy uv 2 wx 2 y uv 3 wx 3 y uwy

Example L 3 = {anbncn: n ≥ 0} • If L 3 has a context-free grammar G, then If uvwxy is in G, so are uv 2 wx 2 y, uv 3 wx 3 y, uwy, . . . • What happens for anbncn? a a a. . . a a b b b. . . b b c c c. . . c c x v w y u • No matter how it is split, uv 2 wx 2 y ∉ L 3!

Pumping lemma for context-free languages • Pumping lemma: For every context-free language L There exists a number n such that for every string z in L, we can write z = uvwxy where |vwx| ≤ n |vx| ≥ 1 For every i ≥ 0, the string uviwxiy is in L. u v w x y

Pumping lemma for context-free languages • So to prove L is not context-free, it is enough that For every n there exists z in L, such that for every way of writing z = uvwxy where |vwx| ≤ n and |vx| ≥ 1, the string uviwxiy is not in L for some i ≥ 0. u v w x y

Proving language is not context-free • Like for regular languages, you need a strategy that always wins you this game 1 2 Donald you choose n write z = uvwxy choose z L choose i you win if uviwxiy L (|vwx| ≤ n, |vx| ≥ 1) At least one is not empty u v w ≤n x y

Example 1 2 Donald you choose n write z = uvwxy choose z L choose i you win if uviwxiy L (|vwx| ≤ n, |vx| ≥ 1) L 3 = {anbncn: n ≥ 0} choose 2 n write z = uvwxy 1 z = anbncn i=? a a a. . . a a b b b. . . b b c c c. . . c c x v w y u

Example • Case 1: v or x contains two kinds of symbols a a a. . . a a b b b. . . b b c c c. . . c c v x Then uv 2 wx 2 y not in L 3 because pattern is wrong • Case 2: v and x both contain one kind of symbol a a a. . . a a b b b. . . b b c c c. . . c c v x Then uv 2 wx 2 y does not have same number of as, bs, cs

More examples L 1 = {anbn: n ≥ 0} ✔ L 2 = {s: s has same number of as and bs} ✔ L 3 = {anbncn: n ≥ 0}✘ L 4 = {ss. R: s ∈ {a, b}*} ✔ L 5 = {ss: s ∈ {a, b}*} Which is context-free?

Example L 5 = {ss: s ∈{a, b}*} 1 2 choose n write z = uvwxy z= n n a i =ba ? b aaaaaaaaab v u What if: w x y aaaaaaaaab u v wx y

Example L 5 = {ss: s {a, b}*} 1 2 z = anbn choose n write z = uvwxy i=? aaaaaabbbbbb u v w x Recall that |vwx| ≤ n y

Example Three cases Case 1: aaaaaabbbbbb Case 2: aaaaaabbbbbb Case 3: aaaaaabbbbbb v x w vwx is in the first half of anbn x v w vwx is in the middle part of anbn x v w vwx is in the second half of anbn

Example Apply pumping with i = 0 Case 1: Case 2: Case 3: aaaaaabbbbbb x v w uwy looks like ajbkanbn, where j < n or k < n aaaaaabbbbbb x v w uwy looks like anbjakbn, where j < n or k < n aaaaaabbbbbb x v w uwy looks like anbnajbk, where j < n or k < n

Example Apply pumping with i = 0 L 5 = {ss: s ∈{a, b}*} uv 0 wx 0 y looks like ajbkanbn, where j < n or k < n Case 1: Not of the form ss Case 2: uv 0 wx 0 y looks like anbjakbn, where j < n or k < n Not of the form ss Case 3: uv 0 wx 0 y looks like anbnajbk, where j < n or k < n Not of the form ss This covers all the cases, so L 5 is not context-free