The Central Limit Theorem What is it and




























- Slides: 46

The Central Limit Theorem: “What is it and how do I present it? ” Dr. Derek Webb Bemidji State University

Outline • • National Standards and the Design of My Talk Available resources Description of central limit theorem In-class simulations Examples Why is the central limit theorem so important? Conclusions 3/9/2021 Dr. Derek Webb Bemidji State University 2

National Standards and the Design of My Talk • Central limit theorem not specifically addressed outside AP course. • Central limit theorem indirectly encountered and discussed in many contexts including simulations, distribution discussions and inferential statistics • My talk provides teachers with background and enables them to incorporate the central limit theorem into their classes if they wish. 3/9/2021 Dr. Derek Webb Bemidji State University 3

National Standards and the Design of My Talk • I attended the National Council of Teachers of Mathematics Academy on Probability and Statistics in Feb. 2004. • Central limit theorem was brought up many times by facilitators and teachers. • Most had a vague (sometimes correct, sometimes incorrect) understanding of the central limit theorem. 3/9/2021 Dr. Derek Webb Bemidji State University 4

What is out there? • Books emphasize theoretical Examples and are brief and unmotivating. • Google search of “central limit theorem” yielded 69, 700 hits. – Pages I visited are technical, complicated, and confusing. – Examples are not very intuitive. 3/9/2021 Dr. Derek Webb Bemidji State University 5

Historical Perspective • 1749 -1827 • Lived in France • First person to study central limit theorem in depth and give a proof of its validity. Pierre-Simon Laplace 3/9/2021 Dr. Derek Webb Bemidji State University 6

Historical Perspective • 1777 -1855 • Lived in Germany • Did extensive work with the normal distribution and probability theory. 3/9/2021 Karl Frederick Gauss Dr. Derek Webb Bemidji State University 7

What is the Central Limit Theorem? 3/9/2021 Dr. Derek Webb Bemidji State University 8

The Central Limit Theorem is not a result about individual observations Individual observations of a random sample: 3/9/2021 Dr. Derek Webb Bemidji State University 9

The Central Limit Theorem describes the properties of the following two quantities as n gets larger The sample mean or average of a random sample of size n: The sum or total of the sample of size n: 3/9/2021 Dr. Derek Webb Bemidji State University 10

In-Class Simulations • Can take lots of time • Many samples necessary • Students may lose track of “big picture” • Multiple class days may be necessary 3/9/2021 Dr. Derek Webb Bemidji State University 11

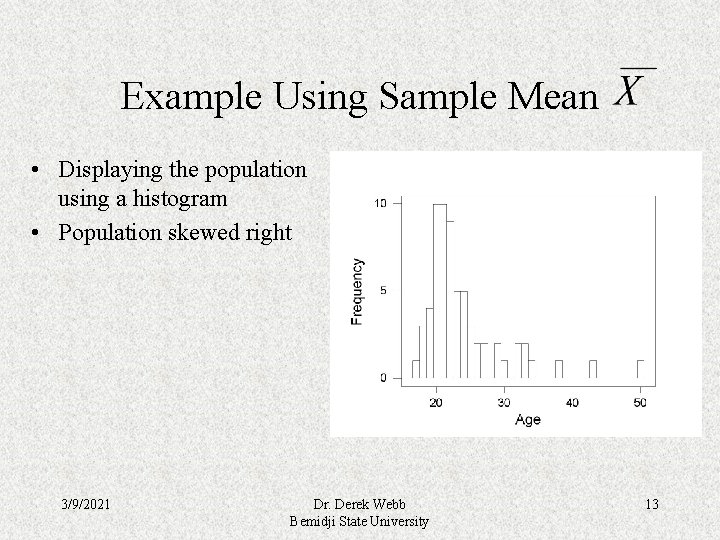
Example Using Sample Mean • Population: 65 introductory statistics students. • Variable: age 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 12

Example Using Sample Mean • Displaying the population using a histogram • Population skewed right 3/9/2021 Dr. Derek Webb Bemidji State University 13

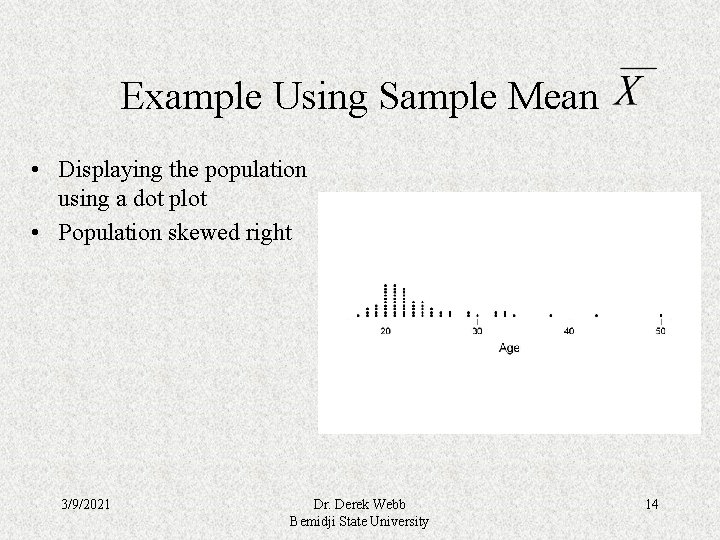
Example Using Sample Mean • Displaying the population using a dot plot • Population skewed right 3/9/2021 Dr. Derek Webb Bemidji State University 14

Sample of Size 1 • Take a random sample of size n=1 from the population. • Sample mean of sample of size n=1 is 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 15

Sample of Size 1 • Take a random sample of size n=1 from the population. • Sample mean of sample of size n=1 is 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 16

Sample of Size 1 • Take a random sample of size n=1 from the population. • Sample mean of sample of size n=1 is 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 17

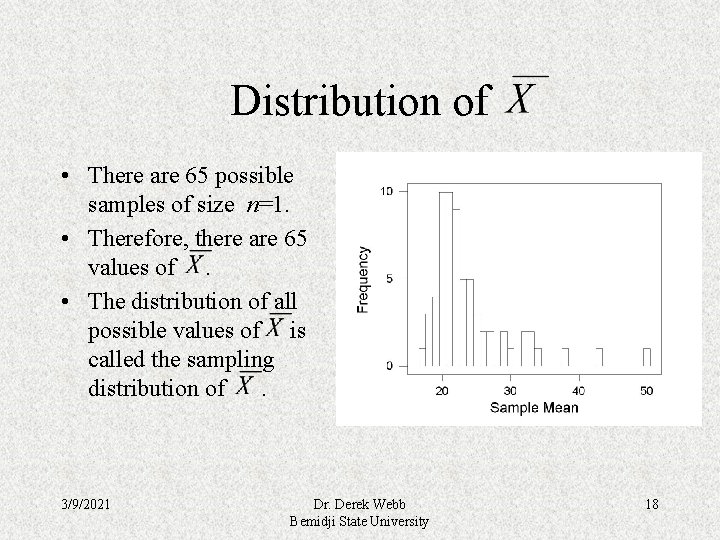
Distribution of • There are 65 possible samples of size n=1. • Therefore, there are 65 values of. • The distribution of all possible values of is called the sampling distribution of. 3/9/2021 Dr. Derek Webb Bemidji State University 18

Sample of Size 2 • Take a random sample of size n=2 from the population. • Sample mean of sample of size n=2 is 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 19

Sample of Size 2 • Take a random sample of size n=2 from the population. • Sample mean of sample of size n=2 is 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 20

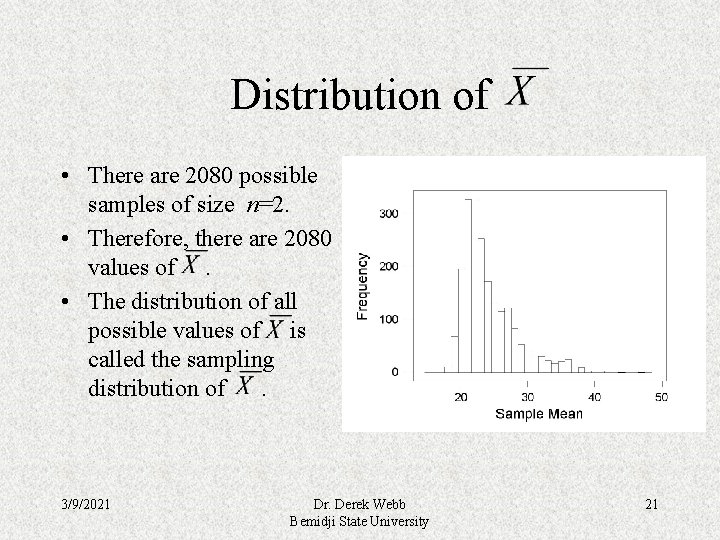
Distribution of • There are 2080 possible samples of size n=2. • Therefore, there are 2080 values of. • The distribution of all possible values of is called the sampling distribution of. 3/9/2021 Dr. Derek Webb Bemidji State University 21

Sample of Size 3 • Take a random sample of size n=3 from the population. • Sample mean of sample of size n=3 is 17 18 18 18 19 19 20 20 20 21 21 21 22 22 22 23 23 23 24 24 24 25 25 25 26 26 27 27 29 29 30 32 32 33 33 34 38 43 50 3/9/2021 Dr. Derek Webb Bemidji State University 22

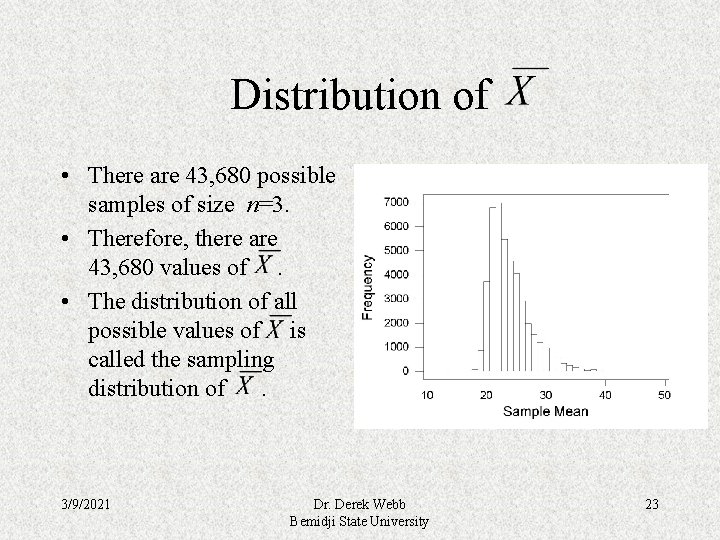
Distribution of • There are 43, 680 possible samples of size n=3. • Therefore, there are 43, 680 values of. • The distribution of all possible values of is called the sampling distribution of. 3/9/2021 Dr. Derek Webb Bemidji State University 23

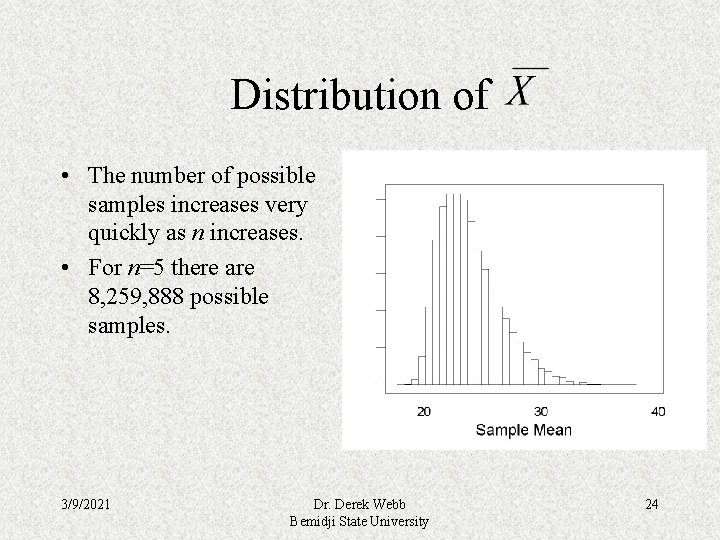
Distribution of • The number of possible samples increases very quickly as n increases. • For n=5 there are 8, 259, 888 possible samples. 3/9/2021 Dr. Derek Webb Bemidji State University 24

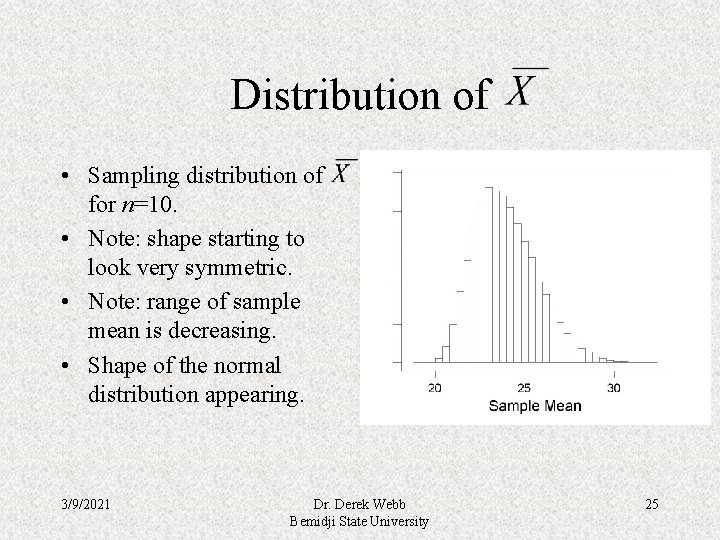
Distribution of • Sampling distribution of for n=10. • Note: shape starting to look very symmetric. • Note: range of sample mean is decreasing. • Shape of the normal distribution appearing. 3/9/2021 Dr. Derek Webb Bemidji State University 25

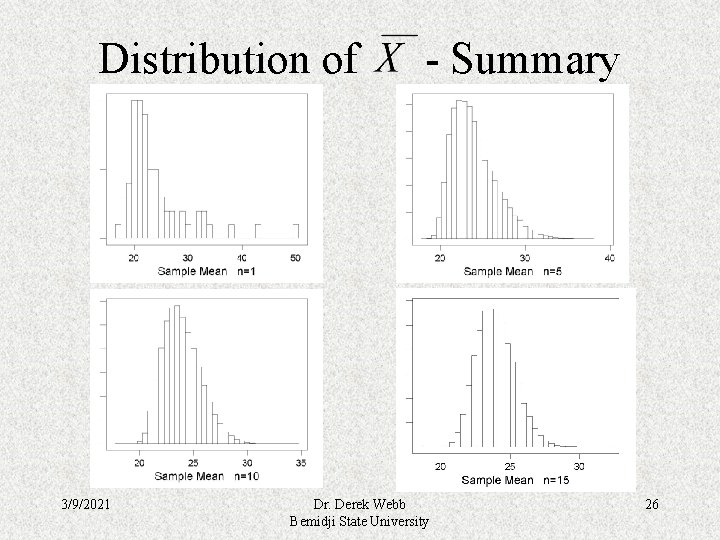
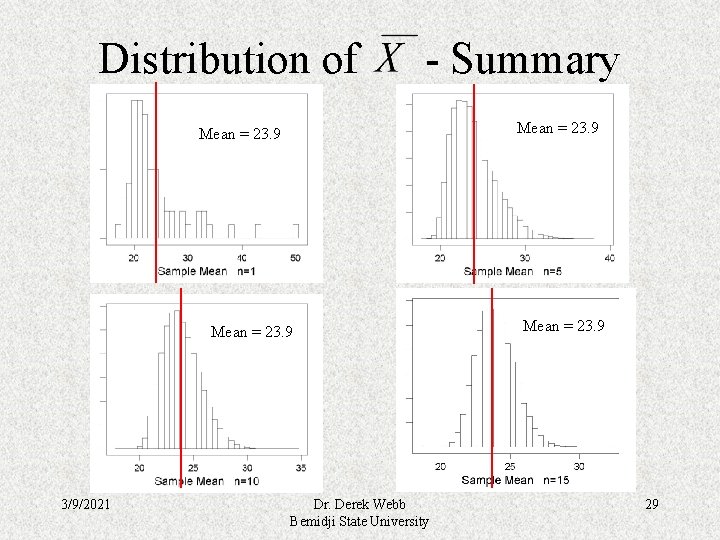
Distribution of 3/9/2021 - Summary Dr. Derek Webb Bemidji State University 26

Distribution of - Summary • The original distribution of ages is very skewed and disjoint. • The distribution of possible values is called the sampling distribution of. • As sample size n increases the sampling distribution of becomes symmetrical. • The larger the sample size, the more closely the distribution resembles the normal distribution. 3/9/2021 Dr. Derek Webb Bemidji State University 27

Distribution of - Summary • The mean of the sampling distribution of equals the mean of the original distribution. The mean of the sampling distribution equals the mean of the original distribution 3/9/2021 Dr. Derek Webb Bemidji State University 28

Distribution of - Summary Mean = 23. 9 3/9/2021 Dr. Derek Webb Bemidji State University Mean = 23. 9 29

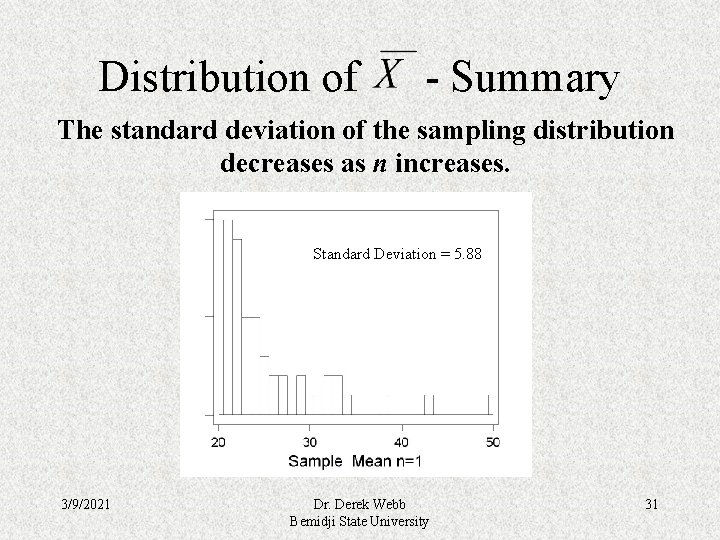
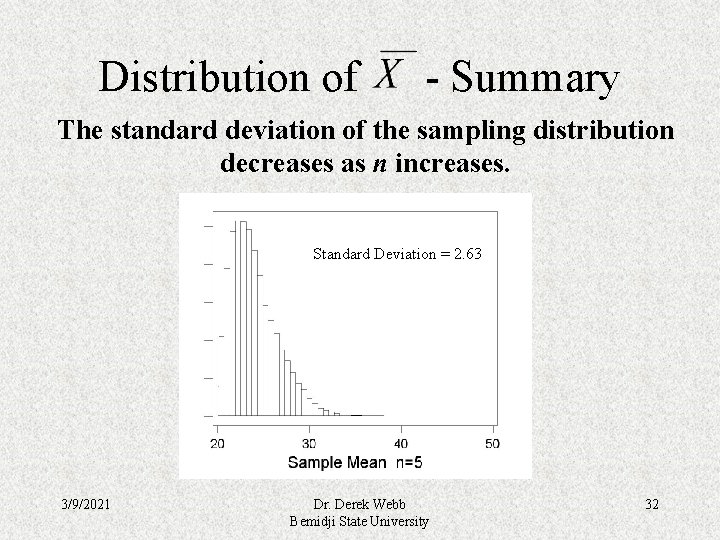
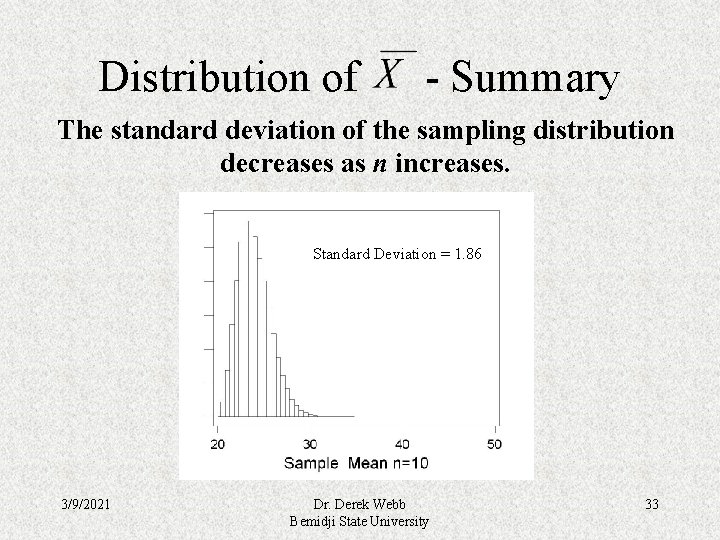
Distribution of - Summary • The standard deviation (spread) of the sampling distribution of equals the standard deviation of the original distribution divided by the square root of the sample size. The standard deviation of the sampling distribution decreases as n increases. 3/9/2021 Dr. Derek Webb Bemidji State University 30

Distribution of - Summary The standard deviation of the sampling distribution decreases as n increases. Standard Deviation = 5. 88 3/9/2021 Dr. Derek Webb Bemidji State University 31

Distribution of - Summary The standard deviation of the sampling distribution decreases as n increases. Standard Deviation = 2. 63 3/9/2021 Dr. Derek Webb Bemidji State University 32

Distribution of - Summary The standard deviation of the sampling distribution decreases as n increases. Standard Deviation = 1. 86 3/9/2021 Dr. Derek Webb Bemidji State University 33

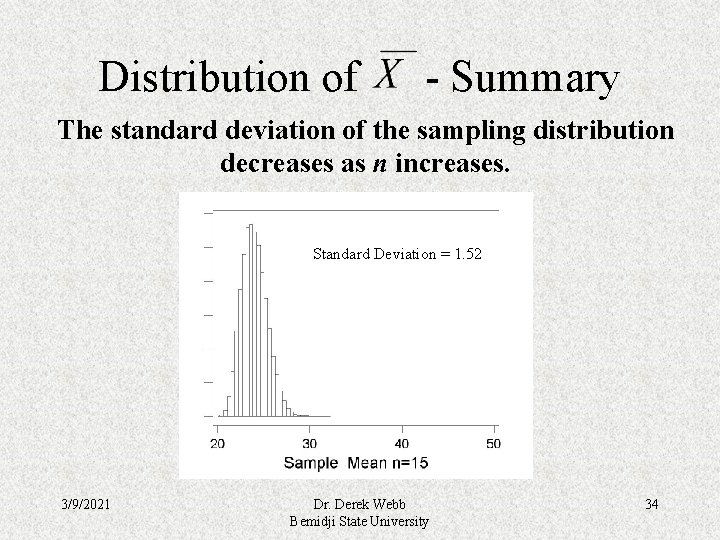
Distribution of - Summary The standard deviation of the sampling distribution decreases as n increases. Standard Deviation = 1. 52 3/9/2021 Dr. Derek Webb Bemidji State University 34

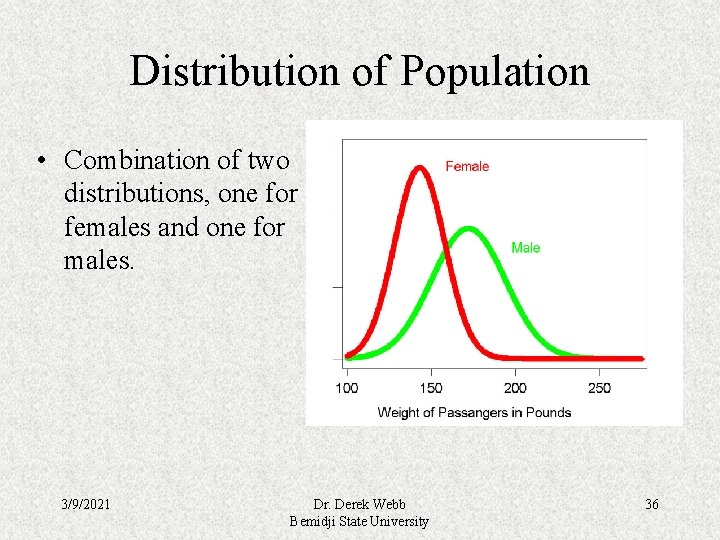
Example Using the Sample Sum: T • Recall • Population: U. S. adults • Sample: Full flight on a Boeing 747 – – – 3/9/2021 Boeing 747 holds 358 passengers Average weight of U. S. male: 172 lbs Average weight of U. S. female: 143 lbs Percent of U. S. population that is male: 49. 1% Percent of U. S. population that is female: 50. 9% Dr. Derek Webb Bemidji State University 35

Distribution of Population • Combination of two distributions, one for females and one for males. 3/9/2021 Dr. Derek Webb Bemidji State University 36

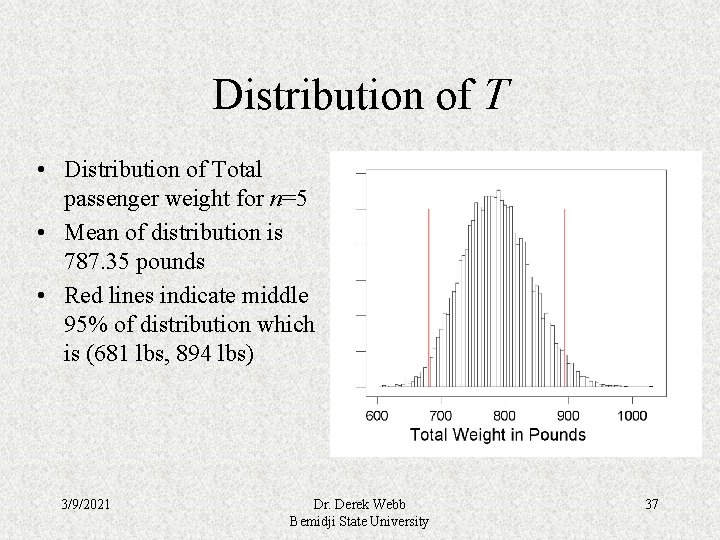
Distribution of T • Distribution of Total passenger weight for n=5 • Mean of distribution is 787. 35 pounds • Red lines indicate middle 95% of distribution which is (681 lbs, 894 lbs) 3/9/2021 Dr. Derek Webb Bemidji State University 37

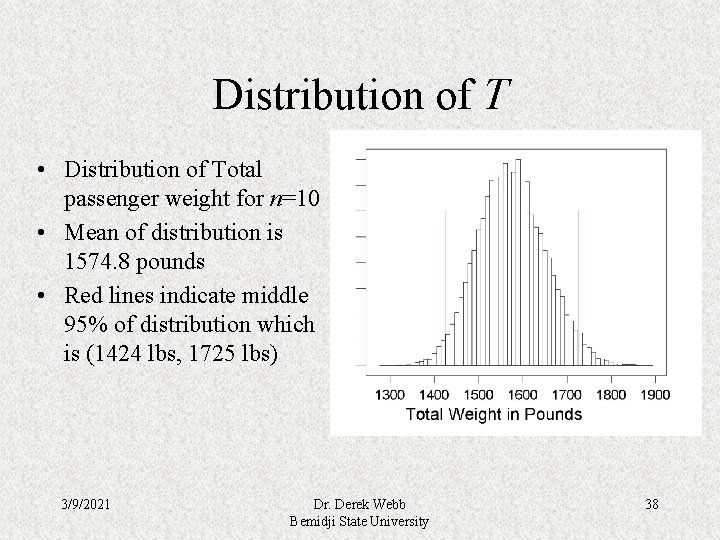
Distribution of T • Distribution of Total passenger weight for n=10 • Mean of distribution is 1574. 8 pounds • Red lines indicate middle 95% of distribution which is (1424 lbs, 1725 lbs) 3/9/2021 Dr. Derek Webb Bemidji State University 38

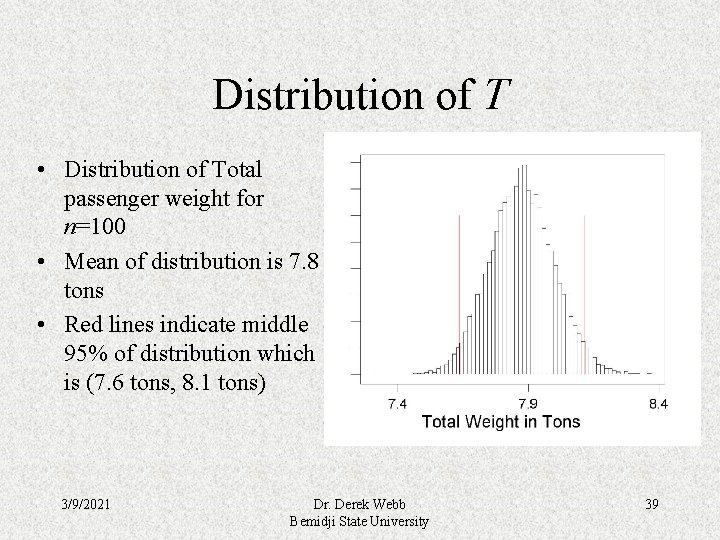
Distribution of T • Distribution of Total passenger weight for n=100 • Mean of distribution is 7. 8 tons • Red lines indicate middle 95% of distribution which is (7. 6 tons, 8. 1 tons) 3/9/2021 Dr. Derek Webb Bemidji State University 39

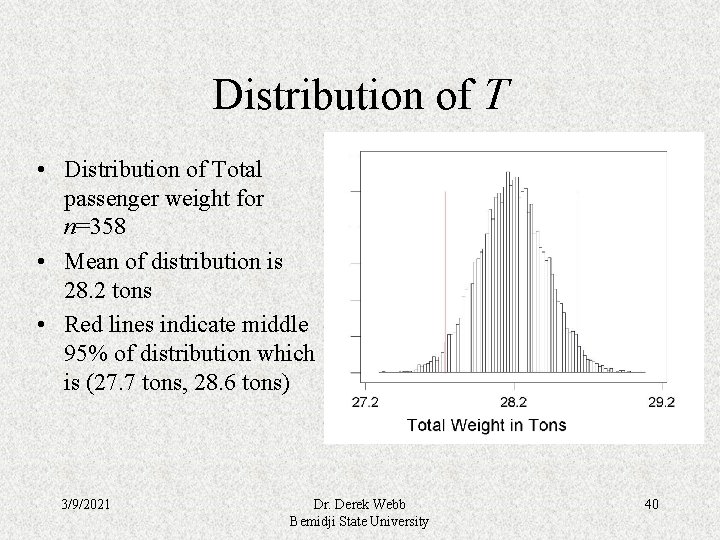
Distribution of T • Distribution of Total passenger weight for n=358 • Mean of distribution is 28. 2 tons • Red lines indicate middle 95% of distribution which is (27. 7 tons, 28. 6 tons) 3/9/2021 Dr. Derek Webb Bemidji State University 40

Distribution of T - Summary • The original distribution of potential adult passengers is complex and non-normal. • The distribution of possible T values is called the sampling distribution of T. • The larger the sample size, the more closely the distribution of T resembles the normal distribution. 3/9/2021 Dr. Derek Webb Bemidji State University 41

Distribution of T - Summary • The mean of the sampling distribution of T equals n times the mean of the original distribution. • The mean of the original distribution is pounds. • The mean of the distribution of T for n=358 is 3/9/2021 Dr. Derek Webb Bemidji State University 42

Distribution of T - Summary • The standard deviation (spread) of the sampling distribution of T equals the square root of the sample size times the standard deviation of the original distribution. • The standard deviation of the original distribution is • The standard deviation of the distribution of T for n=358 is 3/9/2021 Dr. Derek Webb Bemidji State University 43

Why is the Central Limit Theorem so Important? • Most populations we study are not normally distributed. • Elementary hypothesis test and confidence interval methods require a normally distributed population OR large sample size ( ). • These methods are frequently used and oftentimes the only methods students learn. 3/9/2021 Dr. Derek Webb Bemidji State University 44

Why is the Central Limit Theorem so Important? • Teachers and students may notice that a simulation exercise in class results in a histogram that looks normal. • Teachers need to be aware of why it looks normal – ie Teachers need to understand the central limit theorem and know when it shows up in simulation exercises. 3/9/2021 Dr. Derek Webb Bemidji State University 45

Questions? 3/9/2021 Dr. Derek Webb Bemidji State University 46