The Cavendish Experiment A Direct Measurement of The

The Cavendish Experiment A Direct Measurement of The Gravitational Constant G Advanced Lab 2, Fall 2008 Joe Mitchell Brian Reed Johnny Sharp Leah Trafford

The Cavendish Experiment: Outline • Motivation Henry Cavendish – The Importance of The Gravitational Constant G • History – The Cavendish Apparatus and Measurement Experimental Setup • Apparatus – Taking Measurements – Brief Description of Forces • Method 1: Equilibrium Positions – Theory and Procedure

Motivation University of Washington Big G Measurement • G determines the strength of gravitational force between two objects –Fundamental constant of nature • G is important in astrophysics and most any calculation involving gravity –Needed to determine the mass of the Earth and other planets and stars http: //lheawww. gsfc. nasa. gov/~merk/G/apparatus. JPG

Cavendish’s Experimental Setup Cavendish History • Performed in 1797 -1798 by Henry Cavendish • Intent of the experiment was to measure the density of the earth –“G” and the mass of the earth were derived by others after • Cavendish’s results death not improved untilpaper 100 “On years –Boys’ 1894 thelater Newtonian Constant of • Density of earth first G Gravitation”, introduced approximated by Newton using Cavendish at Work

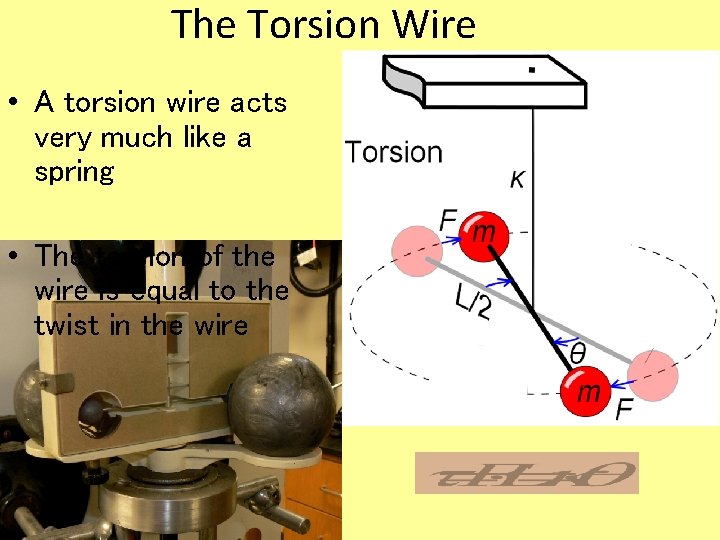
The Torsion Wire • A torsion wire acts very much like a spring • The torsion of the wire is equal to the twist in the wire

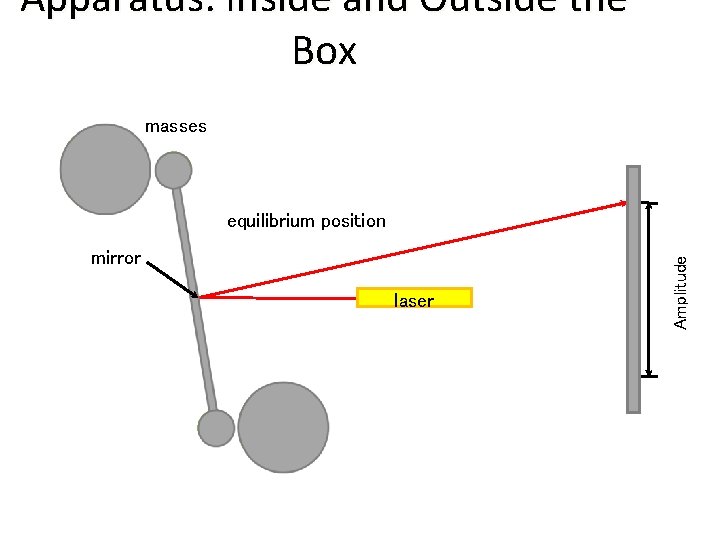
Apparatus: Inside and Outside the Box masses mirror laser Amplitude laser position after one period equilibrium position

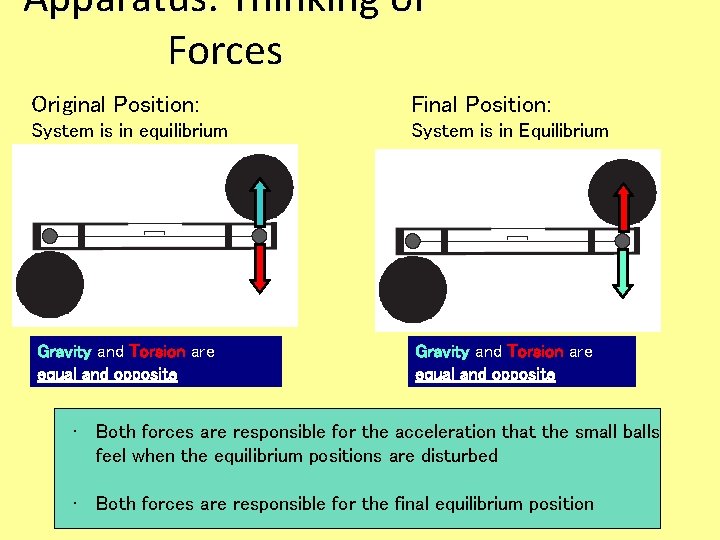
Apparatus: Thinking of Forces Original Position: Final Position: System is in equilibrium System is in Equilibrium Gravity and Torsion are equal and opposite • Both forces are responsible for the acceleration that the small balls feel when the equilibrium positions are disturbed • Both forces are responsible for the final equilibrium position

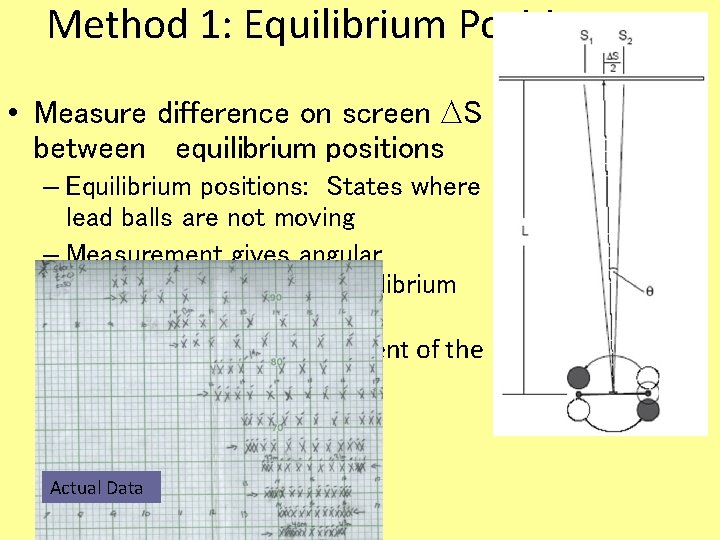
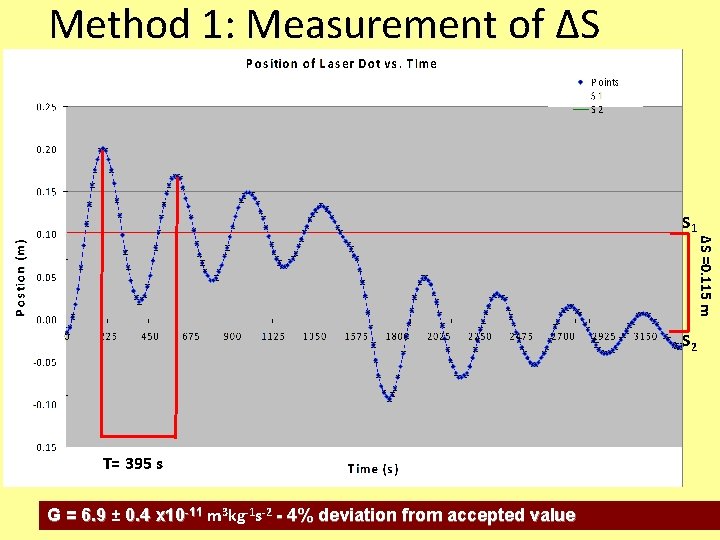
Method 1: Equilibrium Position • Measure difference on screen ∆S between equilibrium positions – Equilibrium positions: States where lead balls are not moving – Measurement gives angular displacement between equilibrium positions – Combine with a measurement of the period to obtain G Actual Data

Method 1: Measurement of ∆S ∆S =0. 115 m S 1 S 2 T= 395 s G = 6. 9 ± 0. 4 x 10 -11 m 3 kg-1 s-2 - 4% deviation from accepted value

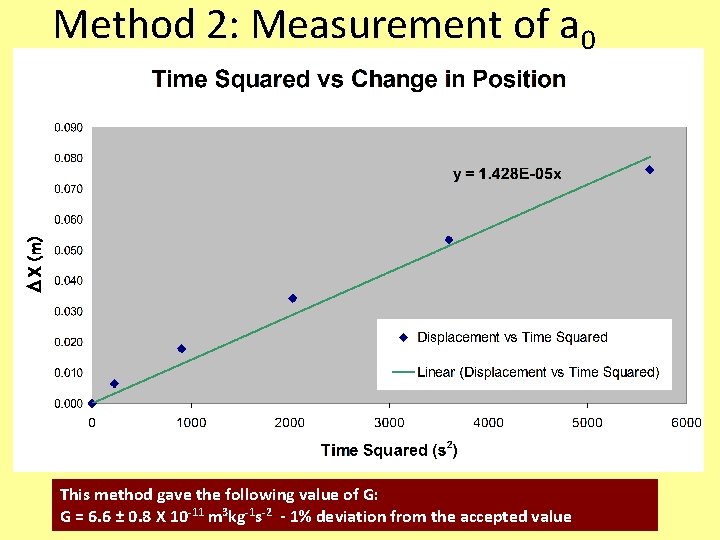
Method 2: Using Acceleration Balls are moved: G can be described in terms of the initial acceleration felt by the small masses Gravity and Torsion are equal and opposite Procedure: 1. Start with large balls in equilibrium position 2. Record Position 3. Flip large balls to final position 4. Record position every 15 seconds for approx. 45 seconds Gravity and Torsion are in the same direction

ΔX (m) Method 2: Measurement of a 0 This method gave the following value of G: G = 6. 6 ± 0. 8 X 10 -11 m 3 kg-1 s-2 - 1% deviation from the accepted value

Summary • G is the fundamental constant with the greatest uncertainty so accurate measurements of it are still important • The search for G began with Cavendish, using a similar method to the one we are implementing • This method uses a torsion balance to measure the gravitational interaction between small spherical weights • To analyze the data and calculate G we used two methods – The equilibrium method: measure the difference