The Breakpoint Graph 2 4 35 1 The

The Breakpoint Graph 2 - 4 35 - 1

The Breakpoint Graph 2 - 4 3 • Augment with 0 = n+1 05 - 1 6

The Breakpoint Graph 0 5 2 - 6 7 4 8 4 3 3 • Augment with 0 = n+1 • Vertices 2 i, 2 i-1 for each i 10 05 - 9 1 2 1 11 6
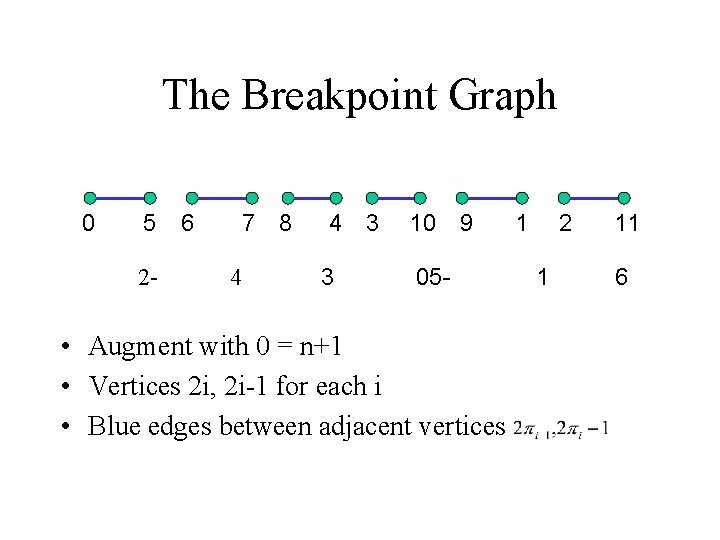
The Breakpoint Graph 0 5 2 - 6 7 4 8 4 3 3 10 9 05 - • Augment with 0 = n+1 • Vertices 2 i, 2 i-1 for each i • Blue edges between adjacent vertices 1 2 1 11 6
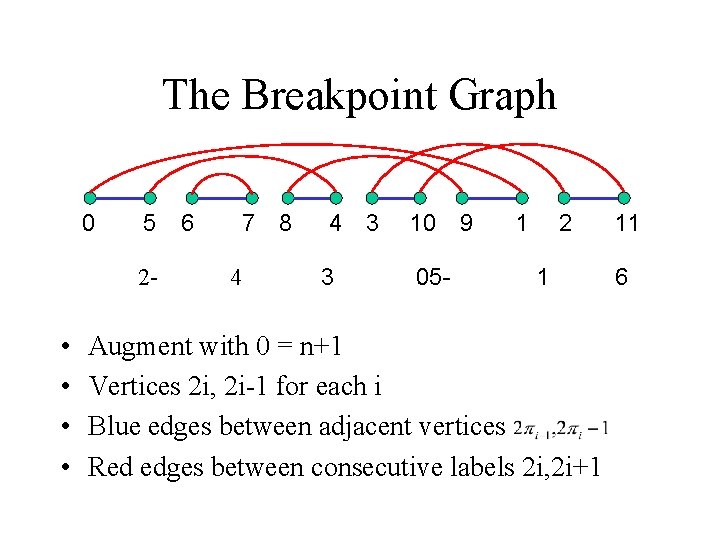
The Breakpoint Graph 0 5 2 - • • 6 7 4 8 4 3 3 10 05 - 9 1 2 1 Augment with 0 = n+1 Vertices 2 i, 2 i-1 for each i Blue edges between adjacent vertices Red edges between consecutive labels 2 i, 2 i+1 11 6
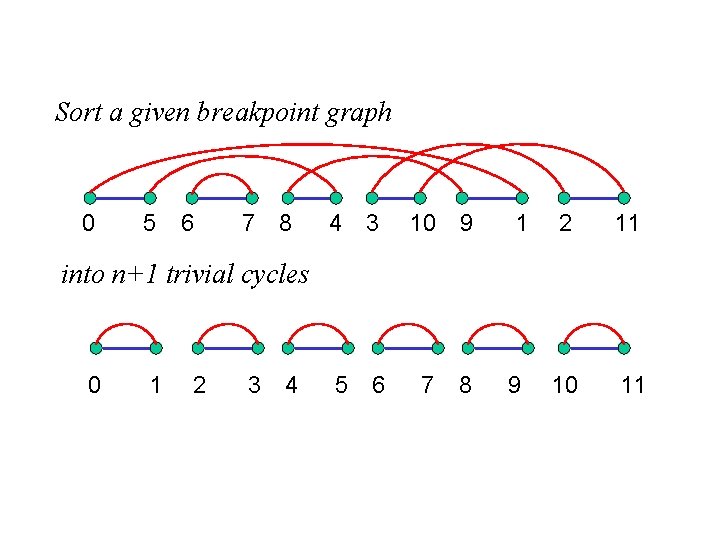
Sort a given breakpoint graph 0 5 6 7 8 4 3 10 9 5 6 7 8 1 2 11 10 11 into n+1 trivial cycles 0 1 2 3 4 9
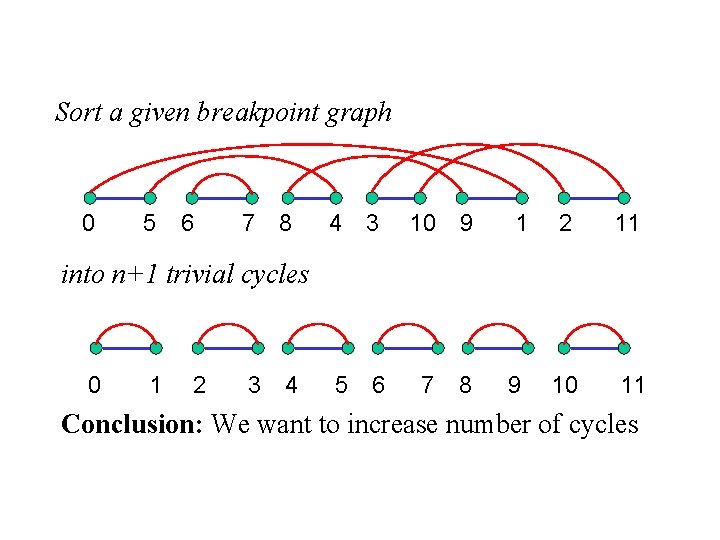
Sort a given breakpoint graph 0 5 6 7 8 4 3 10 9 5 6 7 8 1 2 11 10 11 into n+1 trivial cycles 0 1 2 3 4 9 Conclusion: We want to increase number of cycles
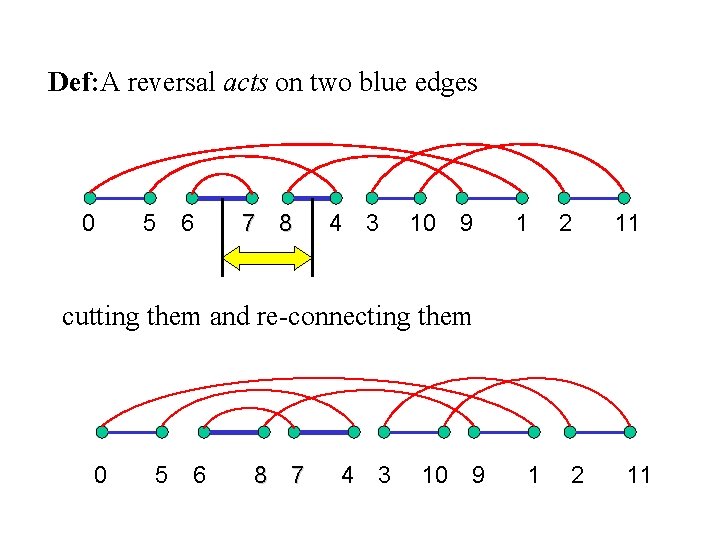
Def: A reversal acts on two blue edges 0 5 6 7 8 4 3 10 9 1 2 11 cutting them and re-connecting them 0 5 6 8 7 4 3 10 9 1 2 11
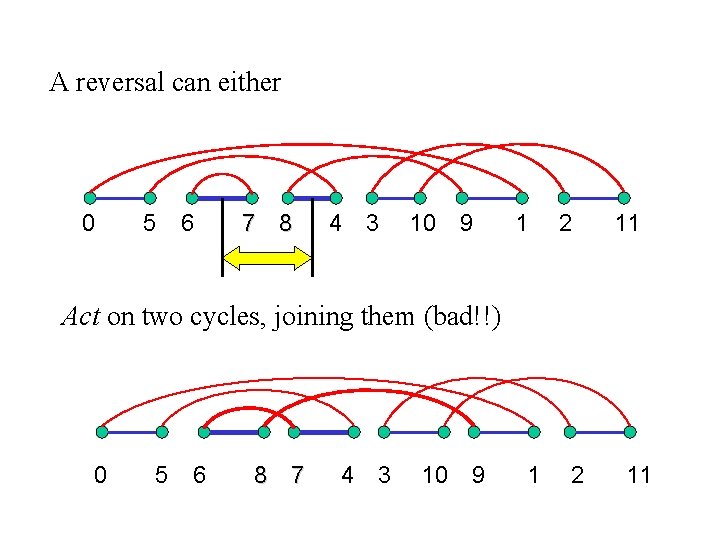
A reversal can either 0 5 6 7 8 4 3 10 9 1 2 11 Act on two cycles, joining them (bad!!) 0 5 6 8 7 4 3 10 9 1 2 11
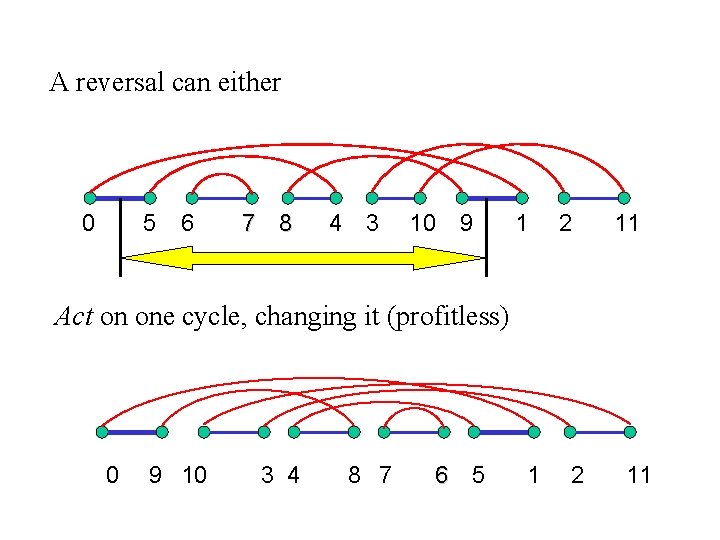
A reversal can either 0 5 6 7 8 4 3 10 9 1 2 11 Act on one cycle, changing it (profitless) 0 9 10 3 4 8 7 6 5 1 2 11
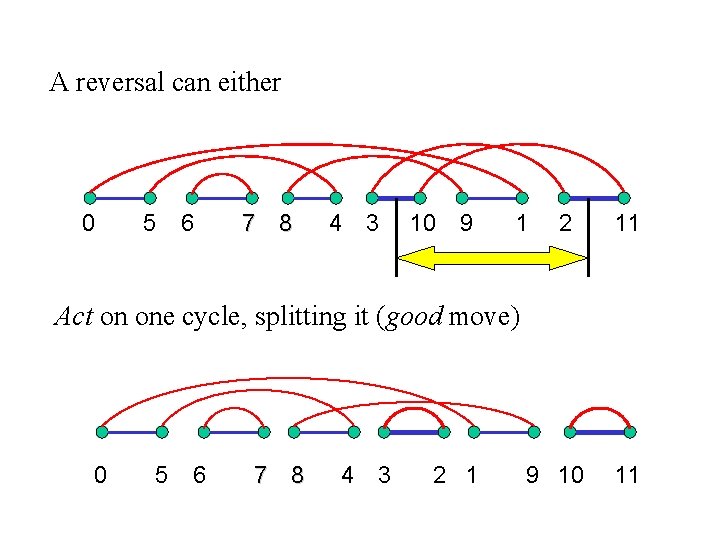
A reversal can either 0 5 6 7 8 4 3 10 9 1 2 11 Act on one cycle, splitting it (good move) 0 5 6 7 8 4 3 2 1 9 10 11

Basic Theorem )Bafna, Pevzner 93( Where d=#reversals needed (reversal distance), and c=#cycles. Proof: Every reversal changes c by at most 1.

Basic Theorem )Bafna, Pevzner 93( Where d=#reversals needed (reversal distance), and c=#cycles. Proof: Every reversal changes c by at most 1. Alternative formulation: where b=#breakpoints, and c ignores short cycles
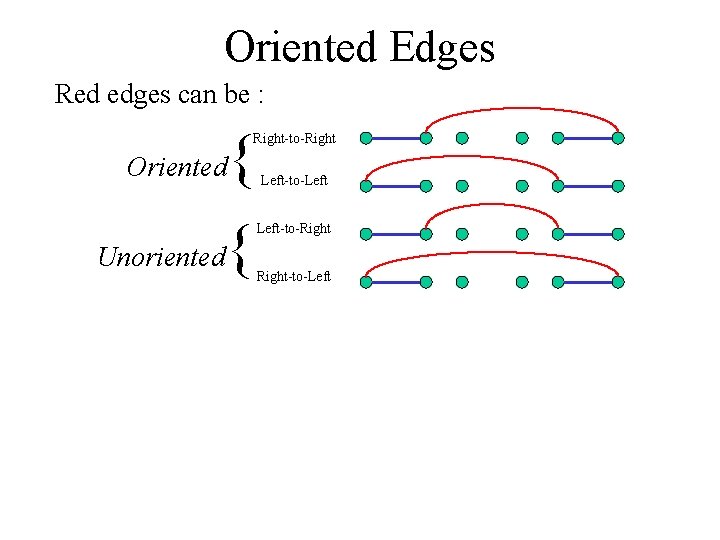
Oriented Edges Red edges can be : { Right-to-Right Oriented Unoriented { Left-to-Left-to-Right-to-Left
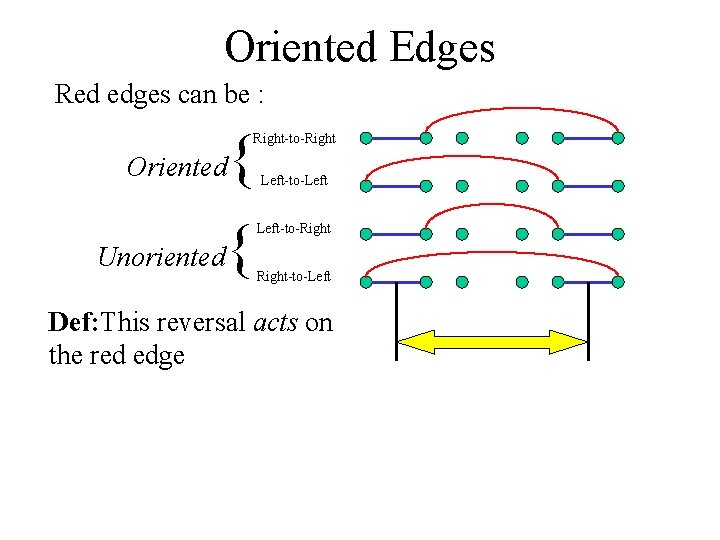
Oriented Edges Red edges can be : { Right-to-Right Oriented Unoriented { Left-to-Left-to-Right-to-Left Def: This reversal acts on the red edge
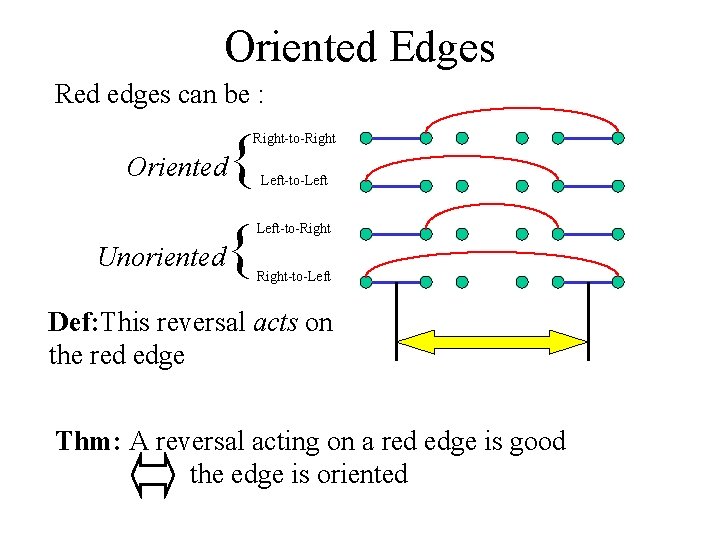
Oriented Edges Red edges can be : { Right-to-Right Oriented Unoriented { Left-to-Left-to-Right-to-Left Def: This reversal acts on the red edge Thm: A reversal acting on a red edge is good the edge is oriented

Overlapping Edges Def: Two red edges are said to be overlapping if they span intersecting intervals which do not contain one another.

Overlapping Edges Def: Two red edges are said to be overlapping if they span intersecting intervals which do not contain one another The lines intersect

Overlapping Edges Def: Two red edges are said to be overlapping if they span intersecting intervals which do not contain one another The lines intersect Thm: A reversal acting on a red edge flips the orientation of all edges overlapping it, leaving other orientations unchanged

Overlapping Edges Def: Two red edges are said to be overlapping if they span intersecting intervals which do not contain one another The lines intersect Thm: if e, f, g overlap each other, then after applying a reversal that acts on e, f and g do not overlap
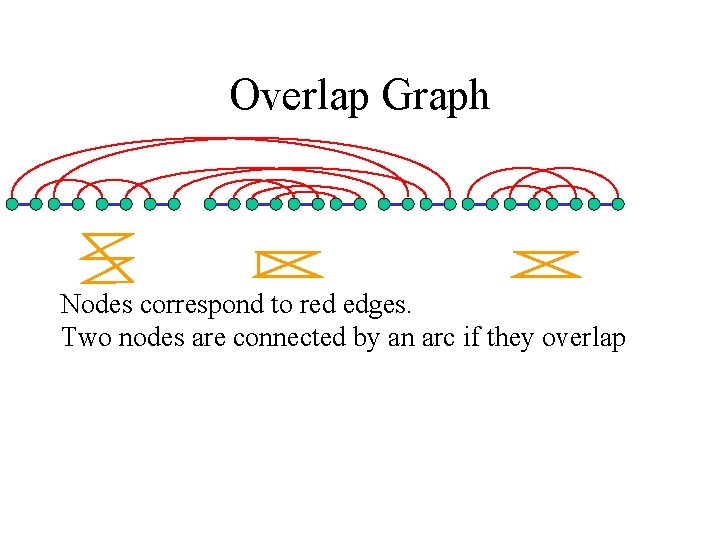
Overlap Graph Nodes correspond to red edges. Two nodes are connected by an arc if they overlap
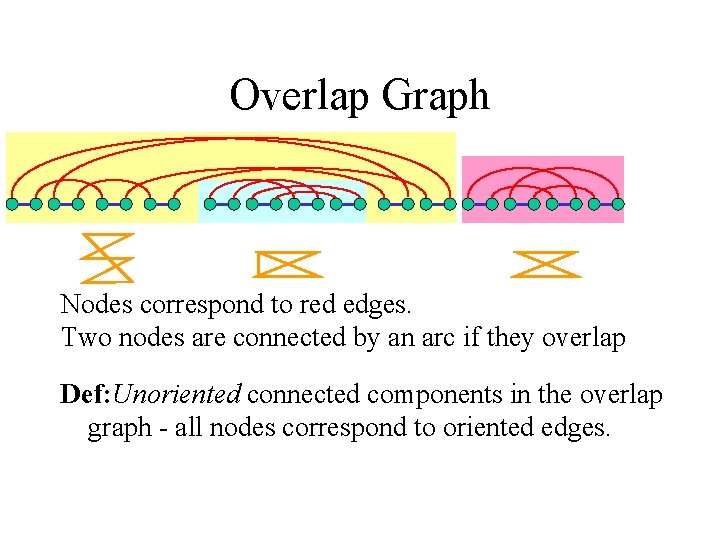
Overlap Graph Nodes correspond to red edges. Two nodes are connected by an arc if they overlap Def: Unoriented connected components in the overlap graph - all nodes correspond to oriented edges.
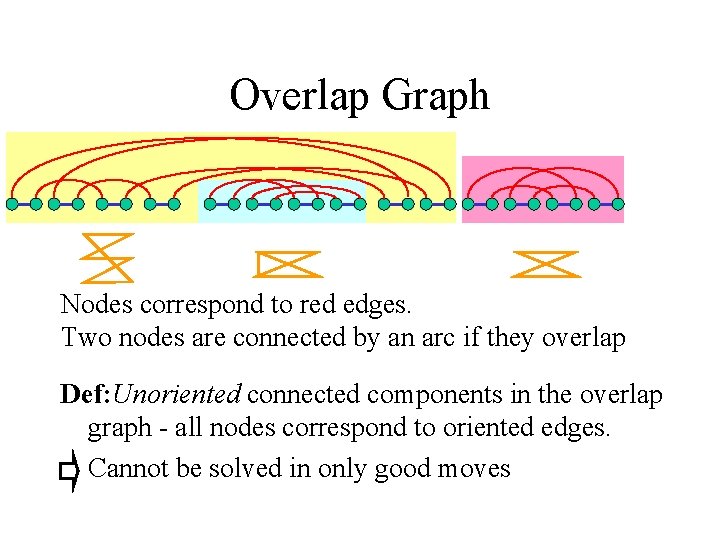
Overlap Graph Nodes correspond to red edges. Two nodes are connected by an arc if they overlap Def: Unoriented connected components in the overlap graph - all nodes correspond to oriented edges. Cannot be solved in only good moves
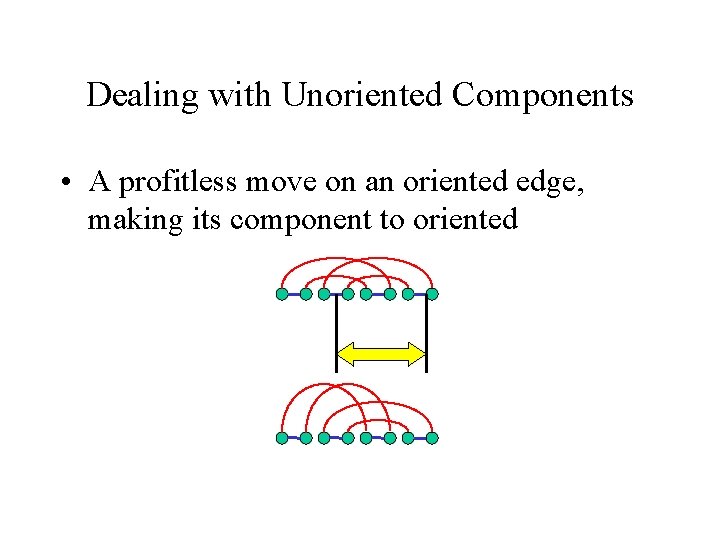
Dealing with Unoriented Components • A profitless move on an oriented edge, making its component to oriented

Dealing with Unoriented Components • A profitless move on an oriented edge, making its component to oriented or: • A bad move (reversal) joining cycles from different unoriented components, thus merging them flipping the orientation of many components on the way
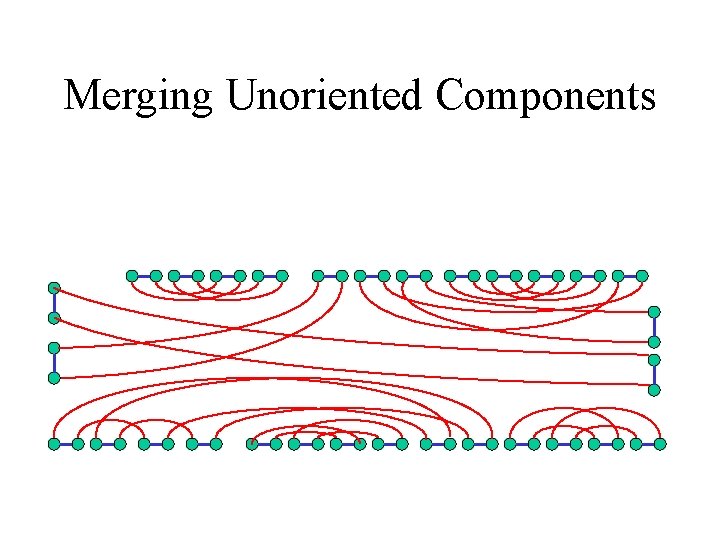
Merging Unoriented Components
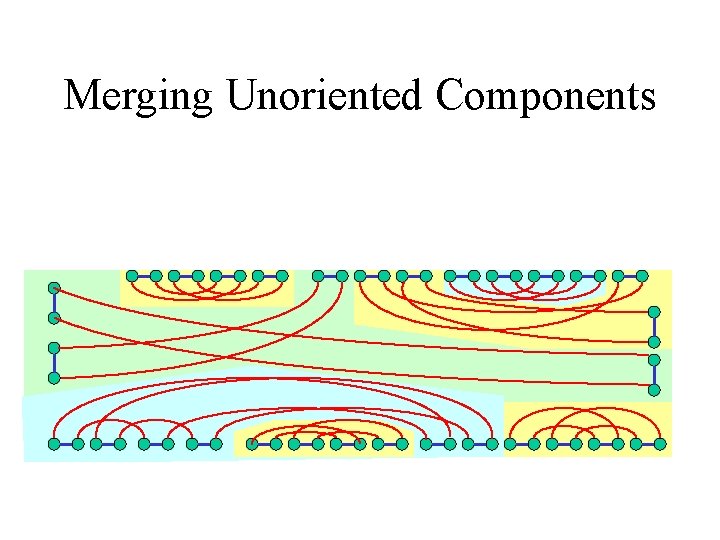
Merging Unoriented Components
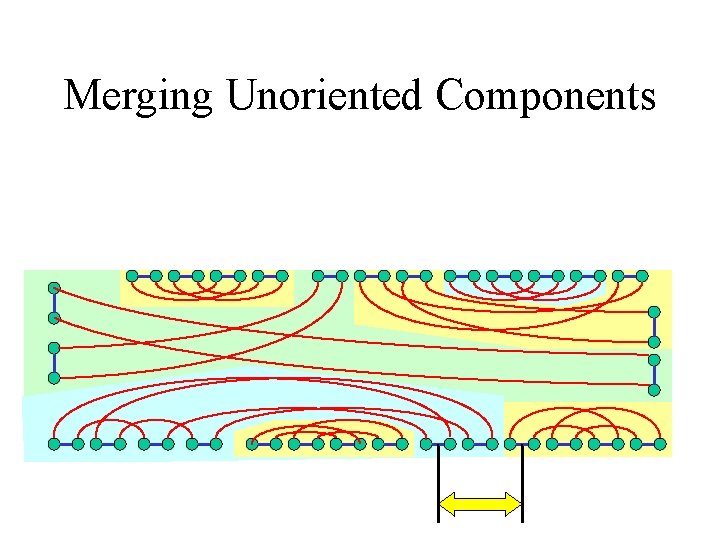
Merging Unoriented Components
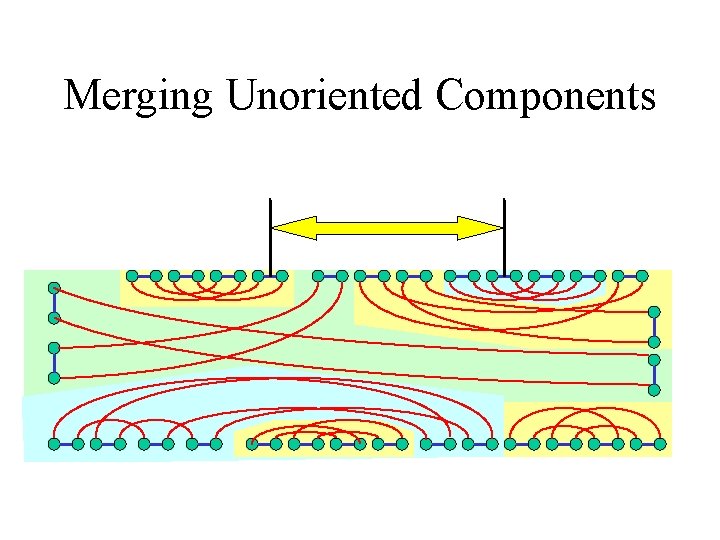
Merging Unoriented Components

Hurdles • Def: Hurdle - an unoriented connected component which is consecutive along the cycle

Hurdles • Def: Hurdle - an unoriented connected component which is consecutive along the cycle • Thm: (Hannenhalli, Pevzner 95) Proof: A hurdle is destroyed by a profitless move, or at most two are destroyed (merged) by a bad move.

Hurdles • Def: Hurdle - an unoriented connected component which is consecutive along the cycle • Thm: (Hannenhalli, Pevzner 95) Proof: A hurdle is destroyed by a profitless move, or at most two are destroyed (merged) by a bad move. • Thm:
- Slides: 32