The Boundary Element Method for atmospheric scattering Problem

The Boundary Element Method for atmospheric scattering • Problem: how do we calculate the scattering pattern from complex particles (ice aggregates, aerosol. . . )?

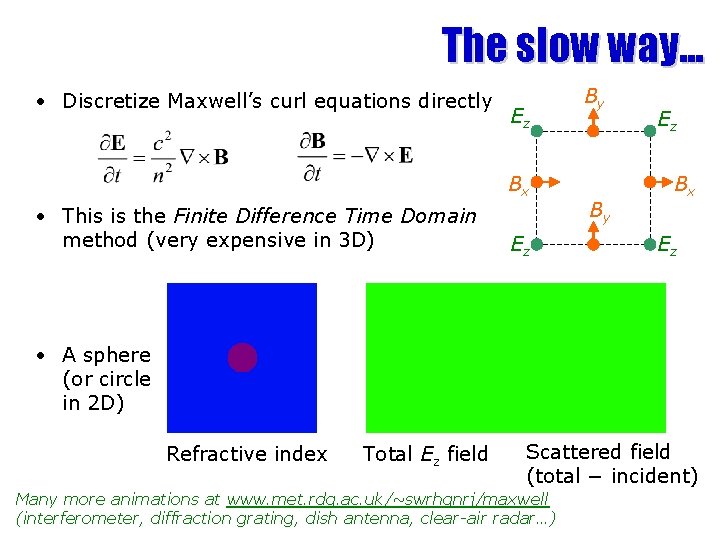
The slow way. . . • Discretize Maxwell’s curl equations directly Ez Bx • This is the Finite Difference Time Domain method (very expensive in 3 D) Ez By By Ez Bx Ez • A sphere (or circle in 2 D) Refractive index Total Ez field Scattered field (total − incident) Many more animations at www. met. rdg. ac. uk/~swrhgnrj/maxwell (interferometer, diffraction grating, dish antenna, clear-air radar…)

The Boundary Element Method • Active research in Maths Dept – Steve Langdon, Simon Chandler-Wilde, Timo Bechte – Mostly applied to acoustic problems – Applicable to EM scattering (but more complicated due to polarization) • Only one paper has applied it to a meteorological problem! • First step: if the source is continuous, we can represent the electric field in time harmonic form: • So we want to find the complex number E(x) everywhere in space (represented by position vector x) that represents the amplitude and phase of the electric field

Green’s representation formula • Need to solve an integral equation: . . . plus the integral over the surface of the object. . Electric field at point x. . . equals the incident wave from source at point x 0. . . Source at x 0 (could be at infinity) . . . of a function of the scattering from the surface at point y to the point x. . Surface s Point on surface y . Point x • As every point on the surface depends on every other point, this boils down to solving a matrix problem

Green functions look like this • Outside the object • Inside the object – Simply the scattering from point on the surface y to point x elsewhere

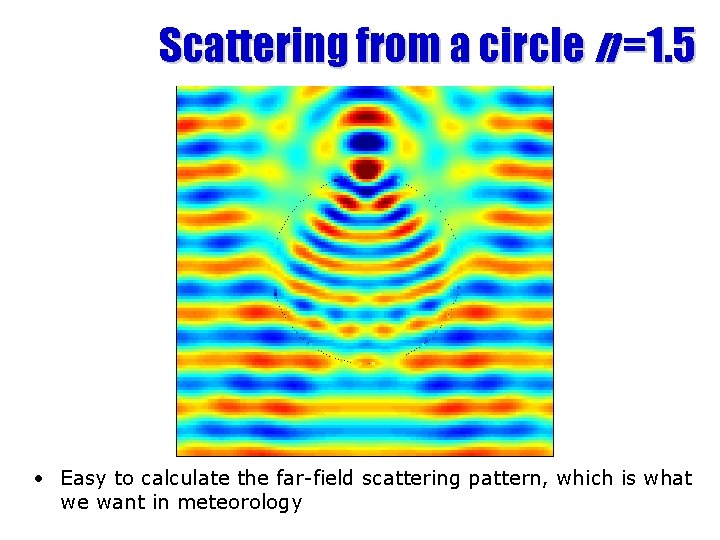
Scattering from a circle n =1. 5 • Easy to calculate the far-field scattering pattern, which is what we want in meteorology

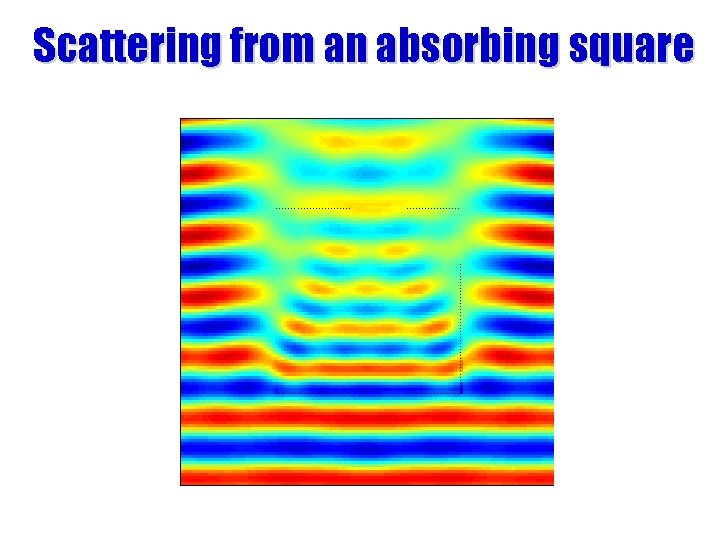
Scattering from an absorbing square

Source need not be a plane wave

Outlook • Potentially very efficient as need only discretize the surface of an object, rather than the entire volume – Number of elements goes as size 2 not size 3 • Still need ~10 points per wavelength • If all the surfaces are flat, it might be possible to represent electric field on each surface by a 2 D Fourier series, requiring only 2 coefficients per wavelength – 5 x 5 = 25 times fewer points • In 3 D, need to use more complicated formula for all three components of the electric field • Rather complicated to code up. . .