The Biological ESTEEM Project Linear Algebra Population Genetics
The Biological ESTEEM Project: Linear Algebra, Population Genetics, and Microsoft Excel Anton E. Weisstein, Truman State University p’ = p (p. WAA + q. WAS) / W

BIO 2010: Transforming Undergraduate Education for Future Research Biologists National Research Council (2003) Recommendation #1: “Those selecting the new approaches should consider the importance of mathematics. . . ” Recommendation #2: “Concepts, examples, and techniques from mathematics…should be included in biology courses. …Faculty in biology, mathematics, and physical sciences must work collaboratively to find ways of integrating mathematics…into life science courses…”

BIO 2010: Transforming Undergraduate Education for Future Research Biologists National Research Council (2003) Specific strategies: • A strong interdisciplinary curriculum that includes physical science, information technology, and math. • Meaningful laboratory experiences.
Biological Topics Tree growth Spread of infectious diseases Enzyme kinetics Population genetics
Mathematical Topics Graph theory Random walks Linear algebra Optimization

Unpacking “ESTEEM” • Excel: ubiquitous, easy, flexible, non-intimidating • Exploratory: apply to real-world data; extend & improve • Experiential: students engage directly with the math
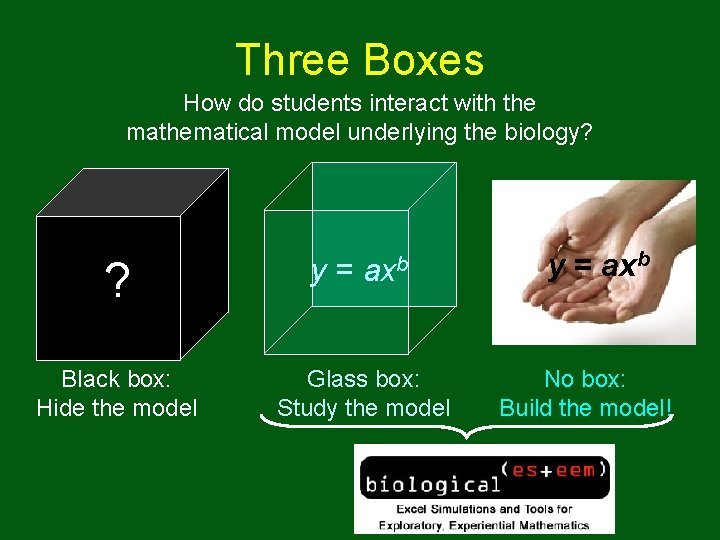
Three Boxes How do students interact with the mathematical model underlying the biology? ? Black box: Hide the model y= axb Glass box: Study the model y = axb No box: Build the model!

Copyleft Users may freely • download • use • modify • share the software, w/proper attribution More info available at Free Software Foundation website

Synthesizing and Applying Math Concepts Using Biological Cases 1. Intro to Population Genetics: Hardy-Weinberg Equilibrium and the Binomial Theorem 2. Evolutionary Analysis: Microevolution, Statistics, and Stability Analysis 3. Survival of the Slightly Better: Exploring an Evolutionary Paradox with Linear Algebra
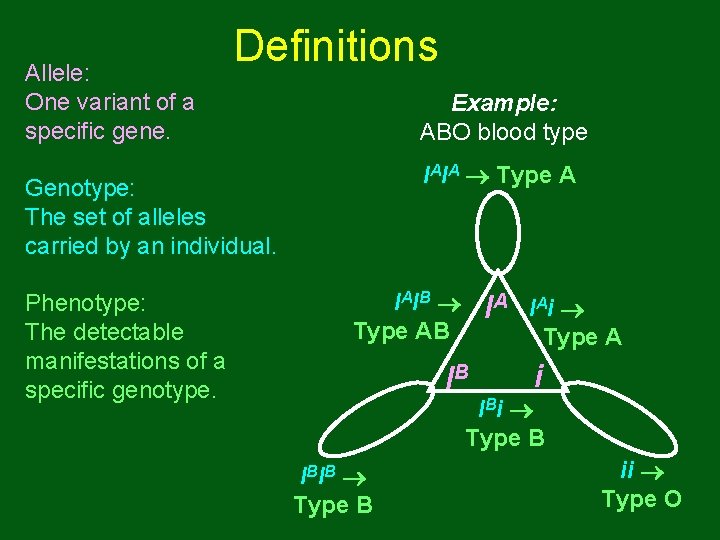
Allele: One variant of a specific gene. Definitions Example: ABO blood type IAIA Type A Genotype: The set of alleles carried by an individual. Phenotype: The detectable manifestations of a specific genotype. I AI B Type AB IA IB I Ai Type A i I Bi Type B I BI B Type B ii Type O
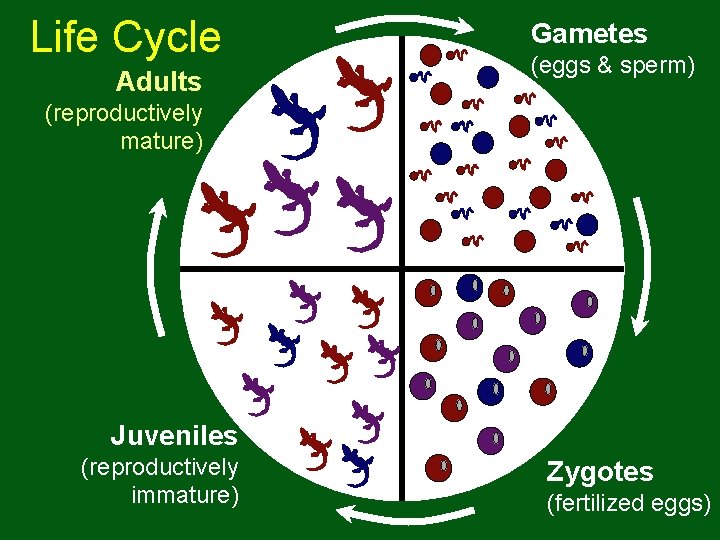
Life Cycle Adults Gametes (eggs & sperm) (reproductively mature) Juveniles (reproductively immature) Zygotes (fertilized eggs)
Life Cycle Adults Gametes (eggs & sperm) (reproductively mature) Juveniles (reproductively immature) Zygotes (fertilized eggs)
Life Cycle Adults Gametes (eggs & sperm) (reproductively mature) Juveniles (reproductively immature) Zygotes (fertilized eggs)
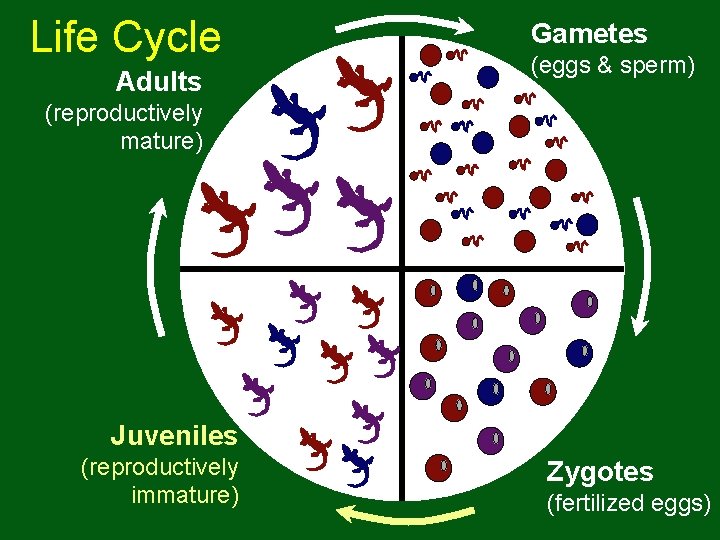
Life Cycle Adults Gametes (eggs & sperm) (reproductively mature) Juveniles (reproductively immature) Zygotes (fertilized eggs)
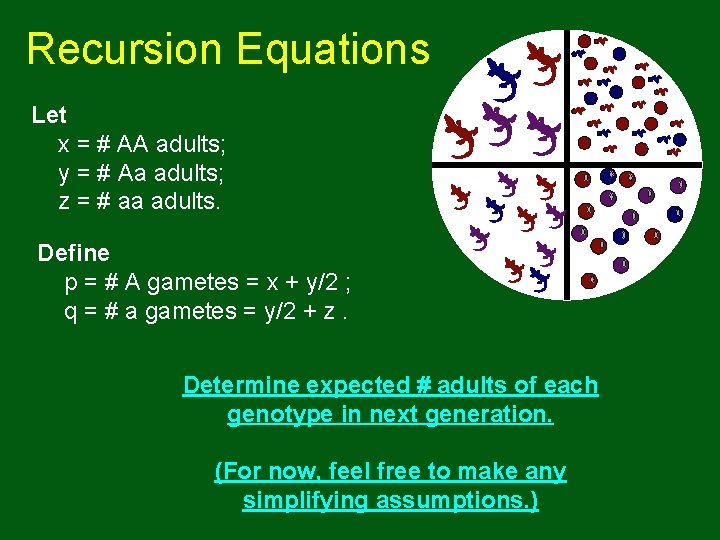
Recursion Equations Let x = # AA adults; y = # Aa adults; z = # aa adults. Define p = # A gametes = x + y/2 ; q = # a gametes = y/2 + z. Determine expected # adults of each genotype in next generation. (For now, feel free to make any simplifying assumptions. )
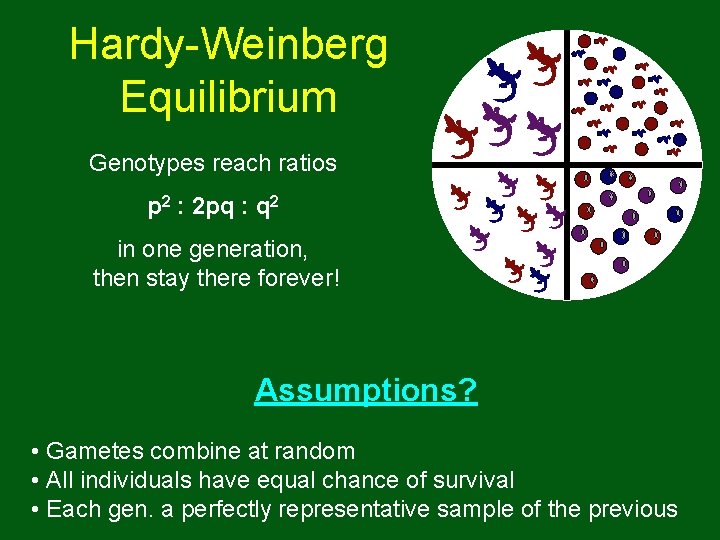
Hardy-Weinberg Equilibrium Genotypes reach ratios p 2 : 2 pq : q 2 in one generation, then stay there forever! Assumptions? • Gametes combine at random • All individuals have equal chance of survival • Each gen. a perfectly representative sample of the previous

Synthesizing and Applying Math Concepts Using Biological Cases 1. Intro to Population Genetics: Hardy-Weinberg Equilibrium and the Binomial Theorem 2. Evolutionary Analysis: Microevolution, Statistics, and Stability Analysis 3. Survival of the Slightly Better: Exploring an Evolutionary Paradox with Linear Algebra
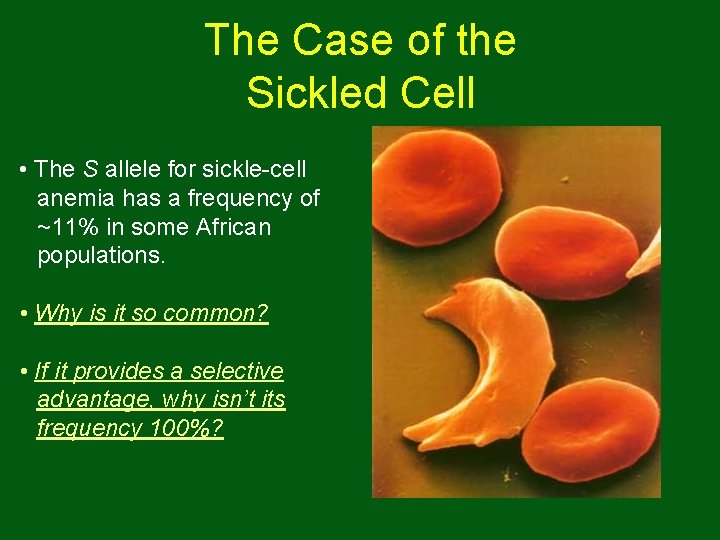
The Case of the Sickled Cell • The S allele for sickle-cell anemia has a frequency of ~11% in some African populations. • Why is it so common? • If it provides a selective advantage, why isn’t its frequency 100%?

Definitions Reproductive fitness: The average number of offspring produced by an organism in a specific environment. Natural selection: An evolutionary mechanism that tends to increase the freq. of traits that increase an organism’s fitness. Examples: • Antibiotic resistance • Camouflage • Resistance to infectious diseases Source: Jeffrey Jeffords, Dive. Gallery. com
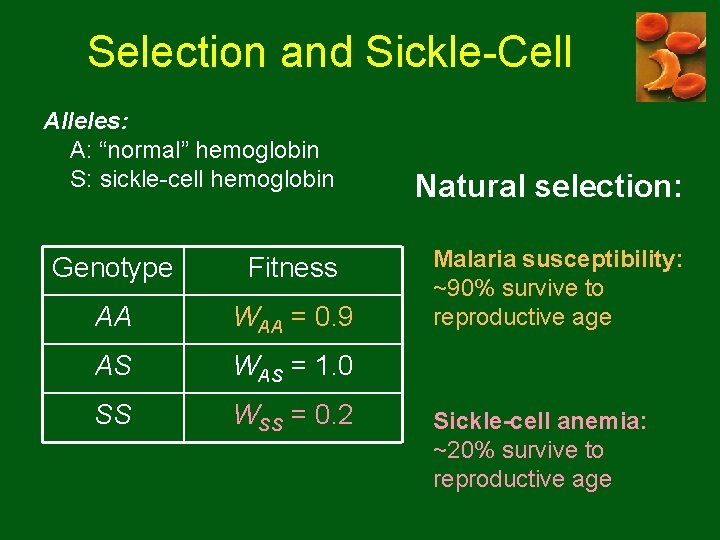
Selection and Sickle-Cell Alleles: A: “normal” hemoglobin S: sickle-cell hemoglobin Genotype Fitness AA WAA = 0. 9 AS WAS = 1. 0 SS WSS = 0. 2 Natural selection: Malaria susceptibility: ~90% survive to reproductive age Sickle-cell anemia: ~20% survive to reproductive age
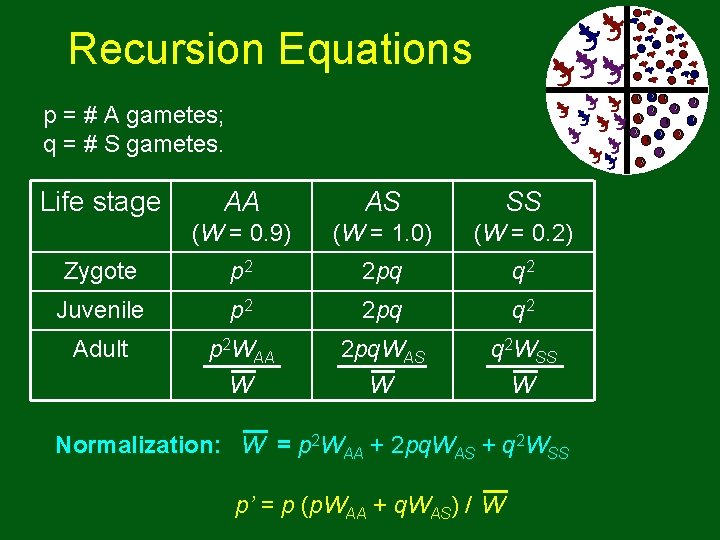
Recursion Equations p = # A gametes; q = # S gametes. Life stage AA AS SS (W = 0. 9) (W = 1. 0) (W = 0. 2) Zygote p 2 2 pq q 2 Juvenile p 2 2 pq q 2 Adult p 2 WAA 2 pq. WAS q 2 WSS W W W Normalization: W = p 2 WAA + 2 pq. WAS + q 2 WSS p’ = p (p. WAA + q. WAS) / W

Selection and Sickle-Cell Genotype Fitness AA WAA = 0. 9 AS WAS = 1. 0 SS WSS = 0. 2 p’ = p (p. WAA + q. WAS) / W Biological Question: Mathematical Question: • How will this population evolve over time? What are the equilibria for this recursion equation?
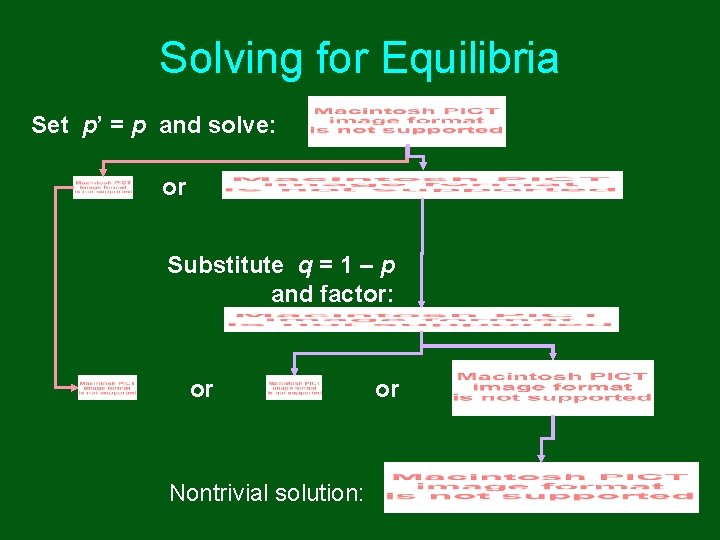
Solving for Equilibria Set p’ = p and solve: or Substitute q = 1 – p and factor: or Nontrivial solution: or
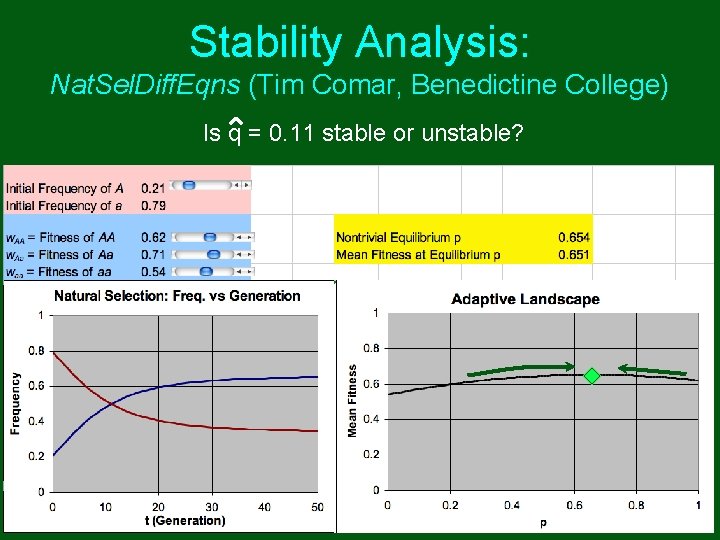
Stability Analysis: Nat. Sel. Diff. Eqns (Tim Comar, Benedictine College) Is q = 0. 11 stable or unstable?

The Case of the Protective Protein • HIV docks with the CCR 5 surface protein present on some cells of immune system • CCR 5 32 allele partially protects against HIV infection Peterson 1999. JYI 2: ?

The Case of the Protective Protein • Based on genetic evidence, 32 arose ~700 years ago. • Present in ~10% of Caucasians; largely absent in other groups. Why? Hypothesis: May also have protected vs. plague and/or smallpox. Biological Question: How much selective advantage must 32 have given to become so common in only 700 years? Mathematical Question: For what fitness values does 700 years lie within the 95% CI of 32’s age?

Definitions Genetic drift: An evolutionary mechanism by which allele frequencies change due to chance alone, independent of those alleles’ effects on fitness. Examples: • Absence of blood type B in Native Americans • Northern elephant seal: virtually no genetic variation 100 years after near-extinction

Modeling Genetic Drift Let N = population size (constant). Assume this pop. produces ∞ gametes: f(A) = p, f(B) =q. But only 2 N of those gametes (chosen at random) combine to form the zygotes that develop into the next generation! p’ = 1 B(2 N, p) ≈ N(p, 2 N pq ) 2 N

Genetic Drift as a Random Walk N = 2000 p’ = 1 B(2 N, p) ≈ N(p, 2 N pq ) 2 N N = 200 N = 20 • Largest fluctuations in small pops. • p = 0 and p = 1 are absorbing states
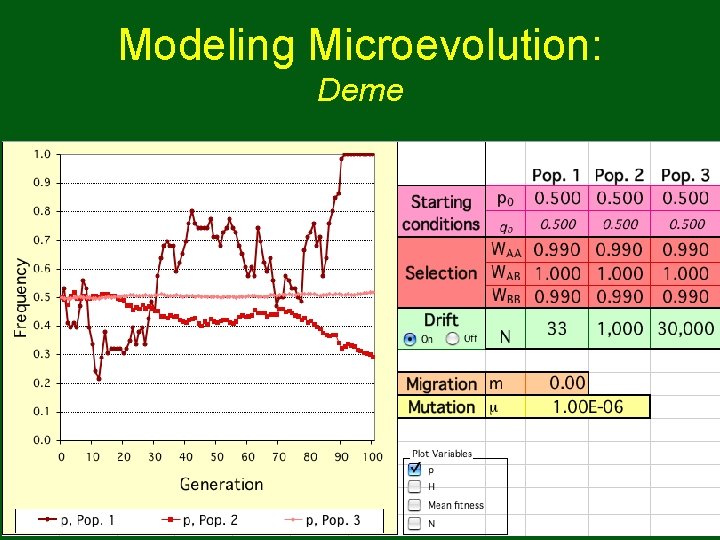
Modeling Microevolution: Deme

Synthesizing and Applying Math Concepts Using Biological Cases 1. Intro to Population Genetics: Hardy-Weinberg Equilibrium and the Binomial Theorem 2. Evolutionary Analysis: Microevolution, Statistics, and Stability Analysis 3. Survival of the Slightly Better: Exploring an Evolutionary Paradox with Linear Algebra
Sickle Cell Strikes Back! • In addition to the A and S alleles, there is also a C allele for hemoglobin! • C confers even stronger malaria resistance than AS but with no anemia! • But C is found only in a few isolated populations. Why might this happen? Extend previous analysis to 3 alleles: some surprising results!
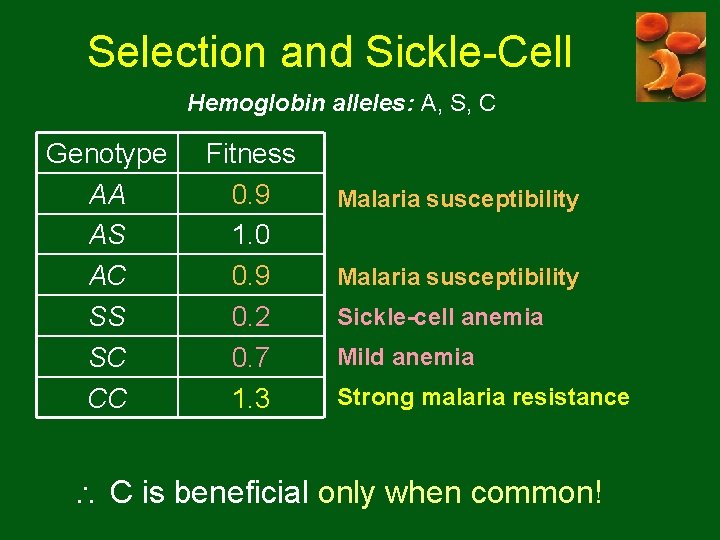
Selection and Sickle-Cell Hemoglobin alleles: A, S, C Genotype AA AS AC SS SC CC Fitness 0. 9 1. 0 0. 9 0. 2 0. 7 1. 3 Malaria susceptibility Sickle-cell anemia Mild anemia Strong malaria resistance C is beneficial only when common!

Selection and Sickle-Cell Recursion Equations: p’ = p (p. WAA + q. WAS + r. WAC) / W q’ = q (p. WAS + q. WSS + r. WSC) / W r’ = r (p. WAC + q. WSC + r. WCC) / W Equilibria: p = DA / D, where q = DS / D, r = DC / D DA = (WAS – WSS)(WAC – WCC) – (WAS – WSC)(WAC – WSC) DS = (WAS – WAA)(WSC – WCC) – (WAS – WAC)(WSC – WAC) DC = (WAC – WAA)(WSC – WSS) – (WAC – WAS)(WSC – WAS) D = DA + DS + DC
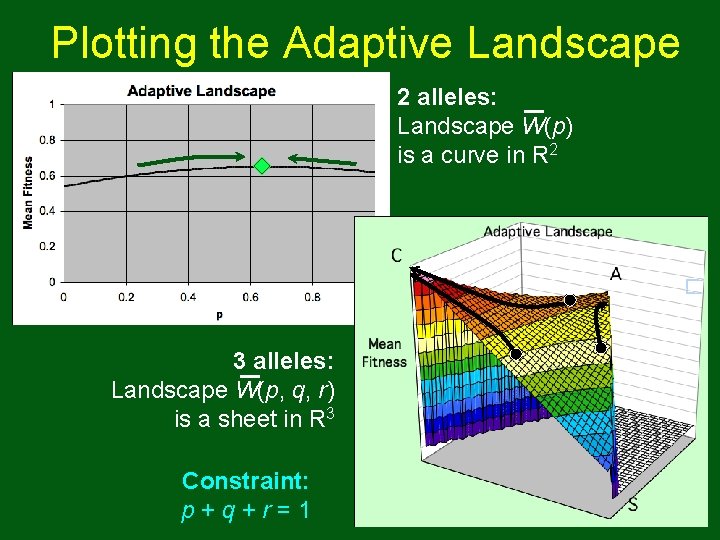
Plotting the Adaptive Landscape 2 alleles: Landscape W(p) is a curve in R 2 3 alleles: Landscape W(p, q, r) is a sheet in R 3 Constraint: p+q+r=1

Stability Analysis 1. Re-express W(p, q, r) as W(x, y) 2. Calculate Hessian matrix: where 3. Take the determinant and apply the 2 nd derivative test: TV > U 2, T > 0, T+V > 0 TV > U 2, T < 0, T+V < 0 TV < U 2 TV = U 2 Local max Local min Saddle point Higher-order tests needed
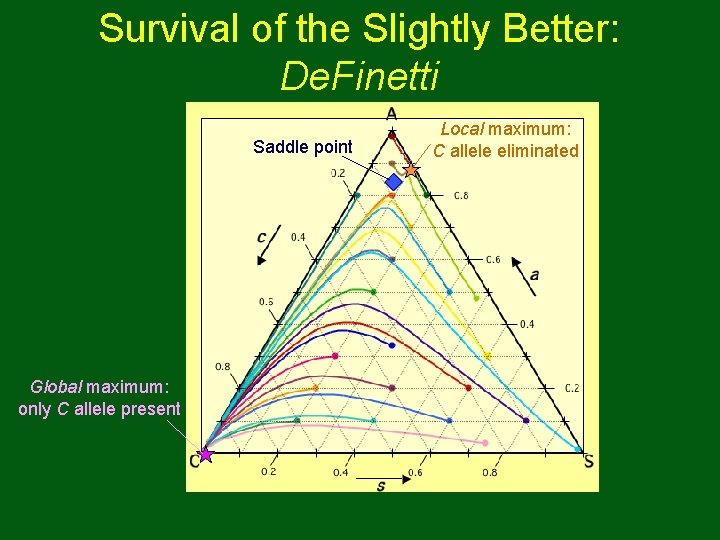
Survival of the Slightly Better: De. Finetti Saddle point Global maximum: only C allele present Local maximum: C allele eliminated

Cases & Mathematics: Explicit Connections • Binomial & Normal Distributions • Combinatorics • Equilibria & Stability Analysis • Normalization • Recursion & Difference Eqns. • Stochasticity • Geometry of Curves & Solids • Matrix & Linear Algebra • Partial Derivatives
- Slides: 38