The Binomial Distribution Permutations How many different pairs

The Binomial Distribution Permutations: How many different pairs of two items are possible from these four letters: L, M. N, P. L, M L, N L, P M, L M, N M, P N, L N, M N, P P, L P, M P, N P = # of Permutations N = # of items r = how many taken at a time

Combinations L, M L, N L, P M, N M, P N, P (order is not important) C = # of Combinations N = # of items r = how many taken at a time

If we flip a single coin, there are two possible outcomes: head or tail (H or T). P(one head) =. 5 P(no head) =. 5 Together the probabilities of these possible outcomes sum to 1. 0. If we flip two coins there are four possible outcomes. H, H H, T T, H T, T P(two heads) =. 25 P(one head) =. 50 P(no heads) =. 25 Total = 1. 0 Can be calculated by… P = P(H) and Q = P(T) Probability of 2 heads Probability of 1 head and 1 tail Or Probability of 2 tails * Think about the frequency distribution.

Flip 3 Coins: 8 possible outcomes H, H, H, T, H, H T, T, H, T, T, T P(3 heads) = 1/8 or. 13 P(2 heads) = 3/8 or. 37 P(1 head) = 3/8 or. 37 P(0 heads) = 1/8 or. 37 Total = 1. 0 Can be calculated by…. . or

Binomial Distribution A binomial distribution is produced when each of a number of Independent trials results in one of two Mutually Exclusive outcomes. A single flip of a coin is a Bernoulli trial. They reflect a discrete variable. P(X) = Probability of X number of an outcome N = Number of trials P = Probability of success on any given trial Q = (1 – P) The number of combinations of N things taken X at a time

Example: Guess if I am thinking of the colour black or white. Because I randomly choose one of the two colours, the probability that I am thinking of black is. 5 on any given trial. There will be 10 trials. What is the probability of guessing 8 of them correctly? = 45(. 009765) =. 0439425 This is the probability of * OR MORE correct, but of exactly 8 out of 10 correct.

Binomial Distribution & Testing a Hypothesis Let us repeat the previous example, but now the question is what is the probability of guessing 8 or more of the trials correctly. We know that P(8) =. 44 That is less than. 05, But that is P(8) against 10, including P(9) and P(10). We need to test the probability of 8 or more correct. P(8) =. 044 P(9) =. 010 P(10) =. 001 Total P =. 055 The probability of guessing 8 or more correctly out of 10 turns out to have a probability greater than. 05, thus we fail to reject the null hypothesis. Which was what?

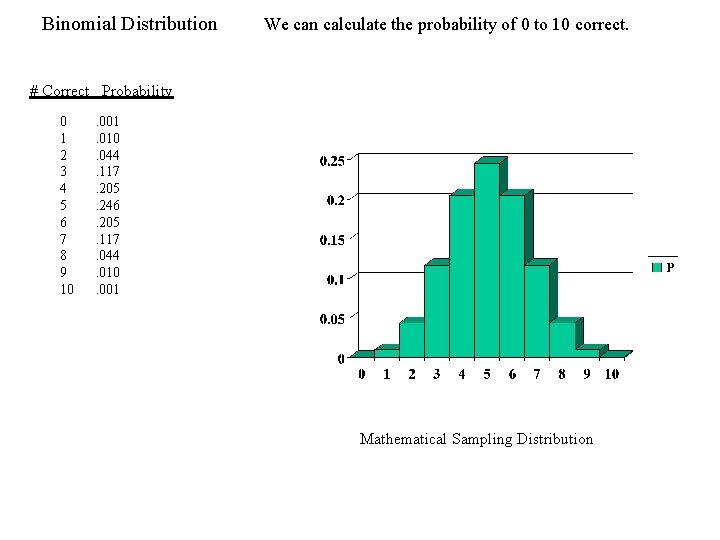
Binomial Distribution We can calculate the probability of 0 to 10 correct. # Correct Probability 0 1 2 3 4 5 6 7 8 9 10 . 001. 010. 044. 117. 205. 246. 205. 117. 044. 010. 001 Mathematical Sampling Distribution

As N gets large, all binomial distributions approach normality, regardless of P. Thus, Mean = NP For example, 10(. 5) = 5 That is, if you examine the data on the previous slide, you will see that the mean of the distribution is 5 (the number of correct trials). Variance = NPQ Standard Deviation = For example, 10(. 5)(. 05) = 2. 25 = 1. 58