The Bernstein Basis and Bezier Curves Dr Scott

The Bernstein Basis and Bezier Curves Dr. Scott Schaefer 1
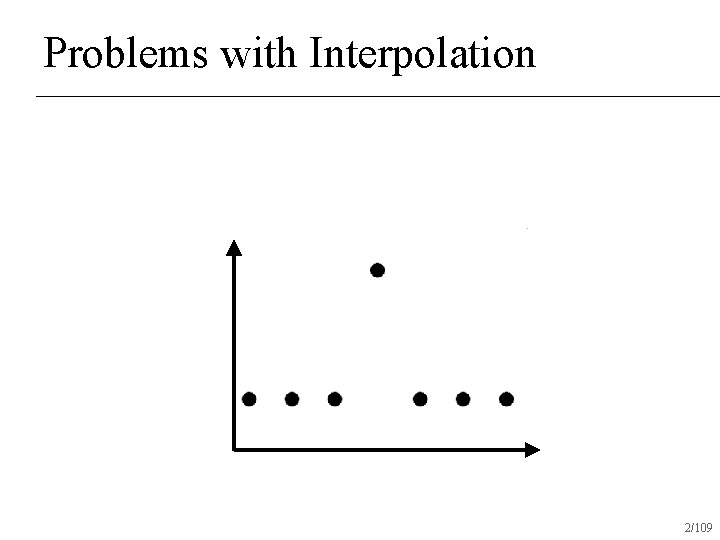
Problems with Interpolation 2/109
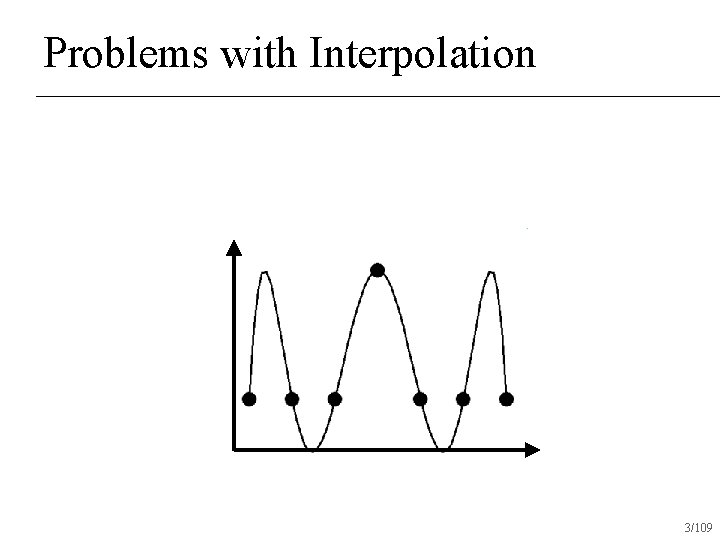
Problems with Interpolation 3/109
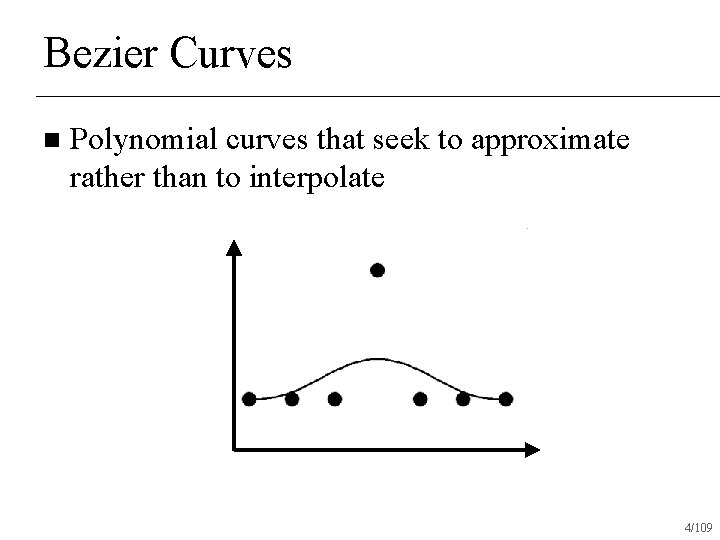
Bezier Curves n Polynomial curves that seek to approximate rather than to interpolate 4/109

Bernstein Polynomials Degree 1: (1 -t), t n Degree 2: (1 -t)2, 2(1 -t)t, t 2 n Degree 3: (1 -t)3, 3(1 -t)2 t, 3(1 -t)t 2, t 3 n 5/109

Bernstein Polynomials Degree 1: (1 -t), t n Degree 2: (1 -t)2, 2(1 -t)t, t 2 n Degree 3: (1 -t)3, 3(1 -t)2 t, 3(1 -t)t 2, t 3 n Degree 4: (1 -t)4, 4(1 -t)3 t, 6(1 -t)2 t 2, 4(1 -t)t 3, t 4 n 6/109

Bernstein Polynomials Degree 1: (1 -t), t n Degree 2: (1 -t)2, 2(1 -t)t, t 2 n Degree 3: (1 -t)3, 3(1 -t)2 t, 3(1 -t)t 2, t 3 n Degree 4: (1 -t)4, 4(1 -t)3 t, 6(1 -t)2 t 2, 4(1 -t)t 3, t 4 n Degree 5: (1 -t)5, 5(1 -t)4 t, 10(1 -t)3 t 2, 10(1 -t)2 t 3 , 5(1 -t)t 4, t 5 n… n Degree n: for n 7/109

Properties of Bernstein Polynomials n 8/109

Properties of Bernstein Polynomials n 9/109

Properties of Bernstein Polynomials n n 10/109

Properties of Bernstein Polynomials n n Binomial Theorem: 11/109

Properties of Bernstein Polynomials n n Binomial Theorem: 12/109

Properties of Bernstein Polynomials n n Binomial Theorem: 13/109

Properties of Bernstein Polynomials n n Binomial Theorem: 14/109

Properties of Bernstein Polynomials n n n 15/109

Properties of Bernstein Polynomials n n n 16/109

Properties of Bernstein Polynomials n n n 17/109

Properties of Bernstein Polynomials n n n 18/109

More Properties of Bernstein Polynomials n 19/109

More Properties of Bernstein Polynomials n n 20/109

More Properties of Bernstein Polynomials n n n 21/109

More Properties of Bernstein Polynomials n n 22/109

Properties of Bernstein Polynomials 23/109

Properties of Bernstein Polynomials n Base case: 24/109

Properties of Bernstein Polynomials n Base case: 25/109

Properties of Bernstein Polynomials n Base case: n Inductive Step: Assume 26/109

Properties of Bernstein Polynomials n Base case: n Inductive Step: Assume 27/109

Properties of Bernstein Polynomials n Base case: n Inductive Step: Assume 28/109

Properties of Bernstein Polynomials n Base case: n Inductive Step: Assume 29/109

Bezier Curves 30/109

Bezier Curves 31/109
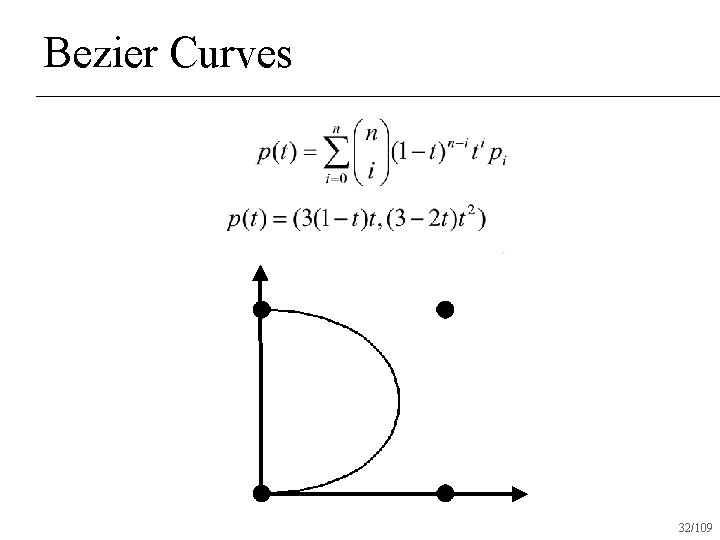
Bezier Curves 32/109

Bezier Curve Properties n Interpolate end-points 33/109

Bezier Curve Properties n Interpolate end-points 34/109

Bezier Curve Properties n Interpolate end-points 35/109
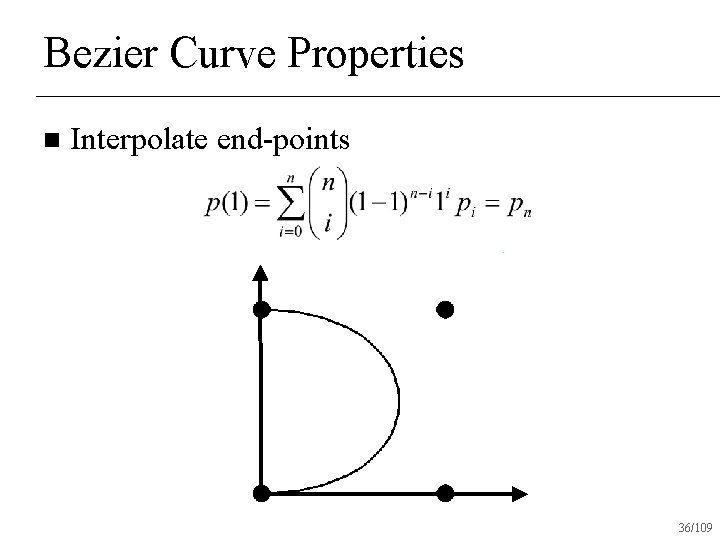
Bezier Curve Properties n Interpolate end-points 36/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n 37/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n 38/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n 39/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n 40/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n 41/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n Another Bezier curve of vectors!!! 42/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n 43/109

Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n Curve lies within the convex hull of the control points n 44/109
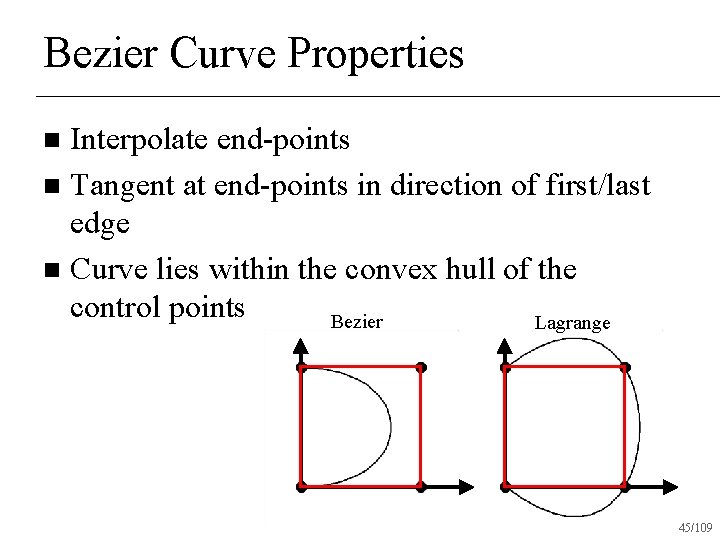
Bezier Curve Properties Interpolate end-points n Tangent at end-points in direction of first/last edge n Curve lies within the convex hull of the control points Bezier Lagrange n 45/109

Matrix Form of Bezier Curves 46/109

Matrix Form of Bezier Curves 47/109

Matrix Form of Bezier Curves 48/109

Matrix Form of Bezier Curves 49/109

Matrix Form of Bezier Curves Computation in monomial basis is unstable!!! Most proofs/computations are easier in Bernstein basis!!! 50/109
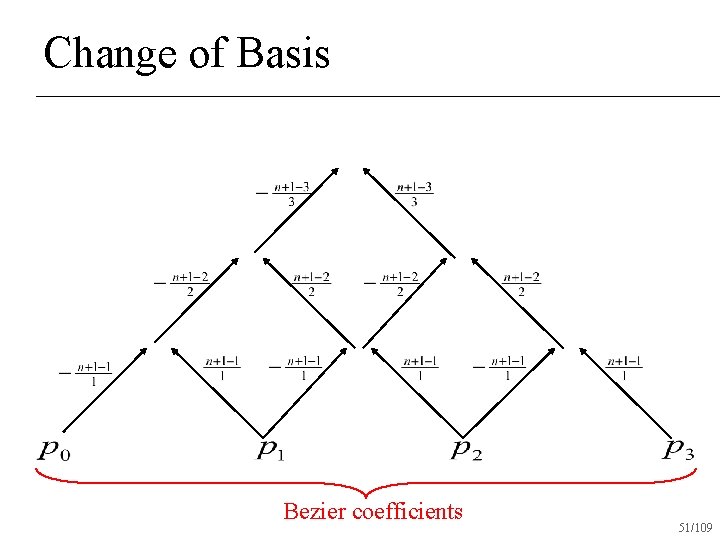
Change of Basis Bezier coefficients 51/109
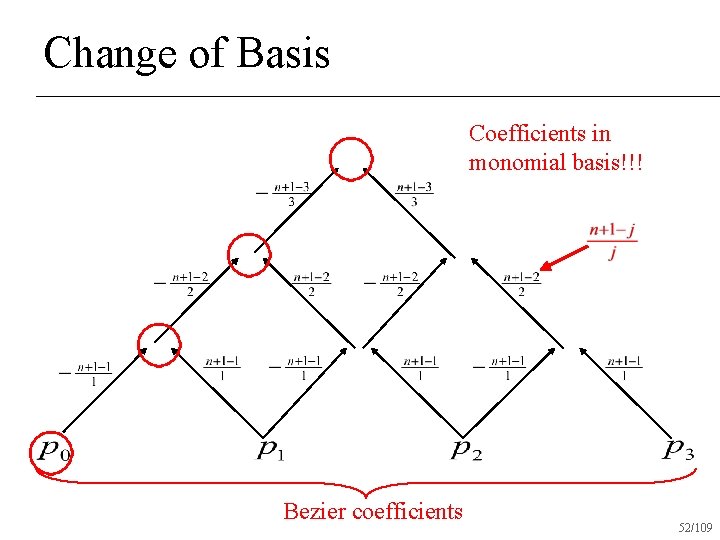
Change of Basis Coefficients in monomial basis!!! Bezier coefficients 52/109
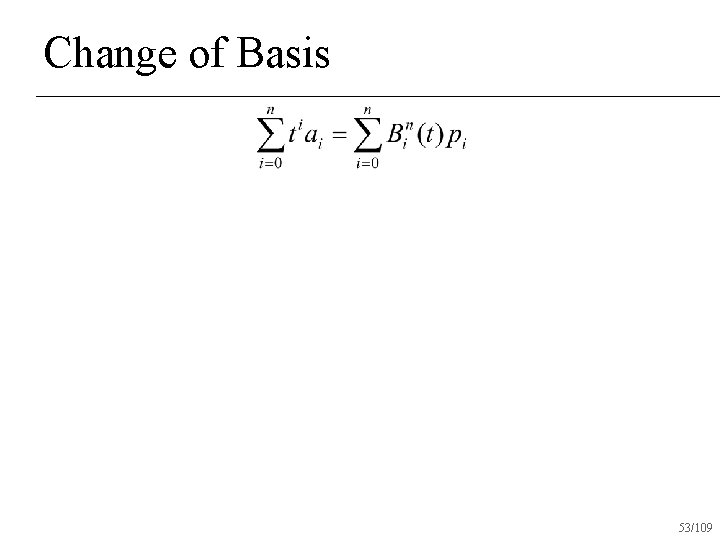
Change of Basis 53/109
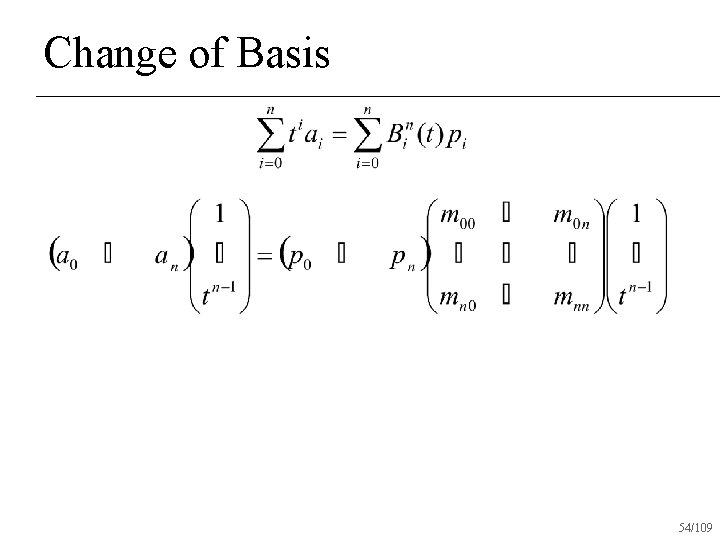
Change of Basis 54/109
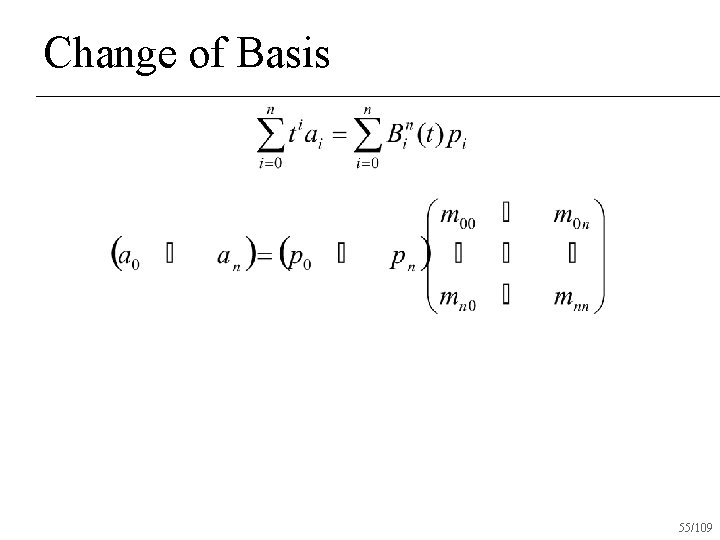
Change of Basis 55/109
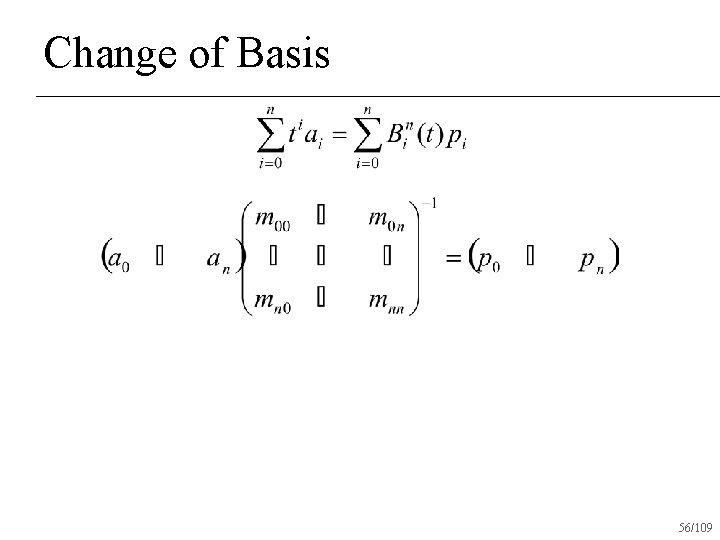
Change of Basis 56/109
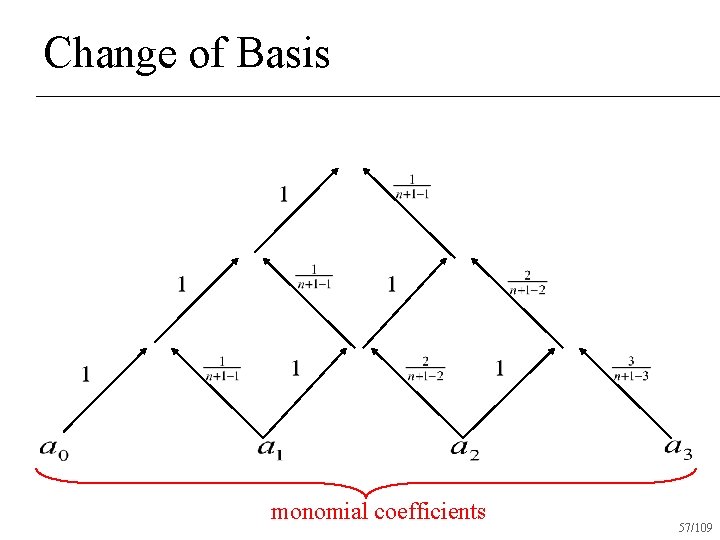
Change of Basis monomial coefficients 57/109
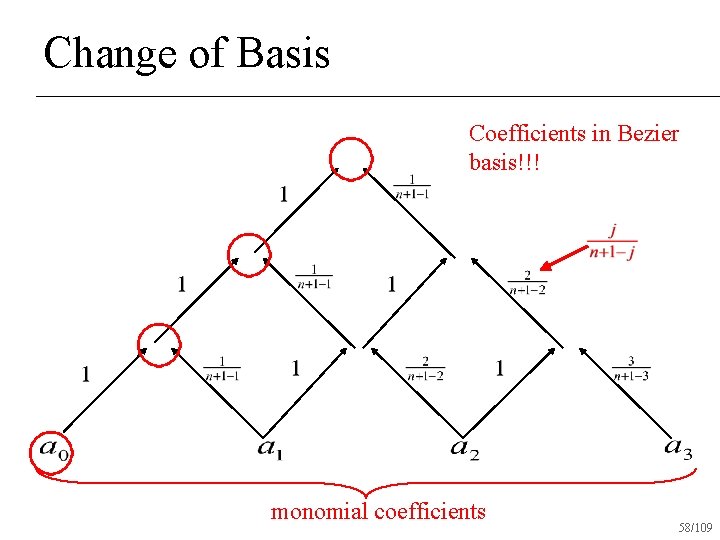
Change of Basis Coefficients in Bezier basis!!! monomial coefficients 58/109

Degree Elevation Power basis is trivial: add 0 tn+1 n What about Bezier basis? n 59/109

Degree Elevation 60/109

Degree Elevation 61/109

Degree Elevation 62/109

Degree Elevation 63/109
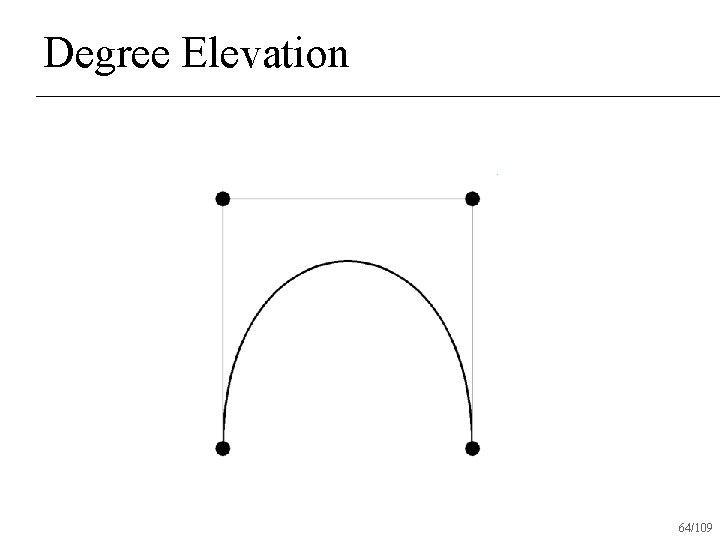
Degree Elevation 64/109
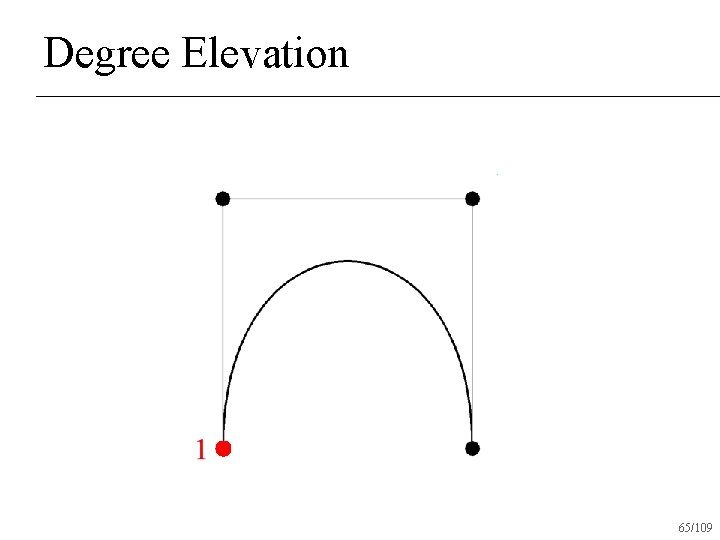
Degree Elevation 65/109
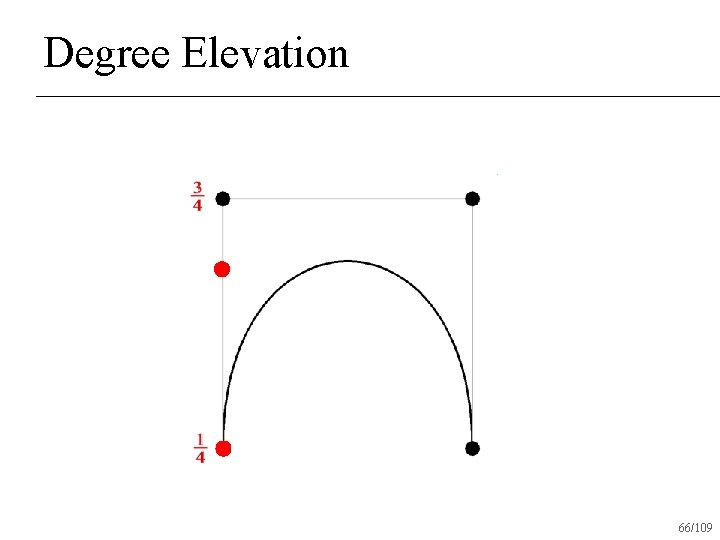
Degree Elevation 66/109
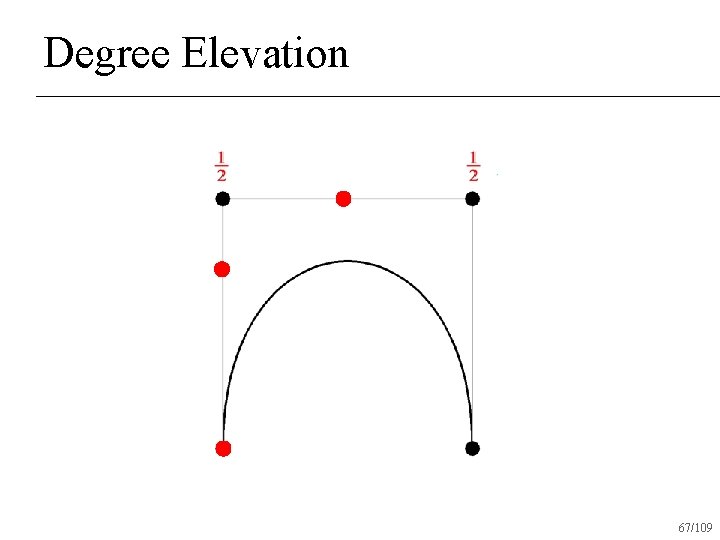
Degree Elevation 67/109
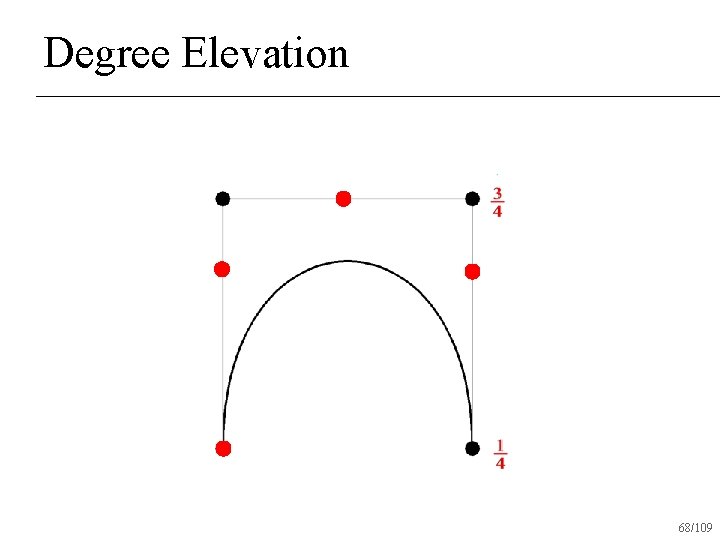
Degree Elevation 68/109
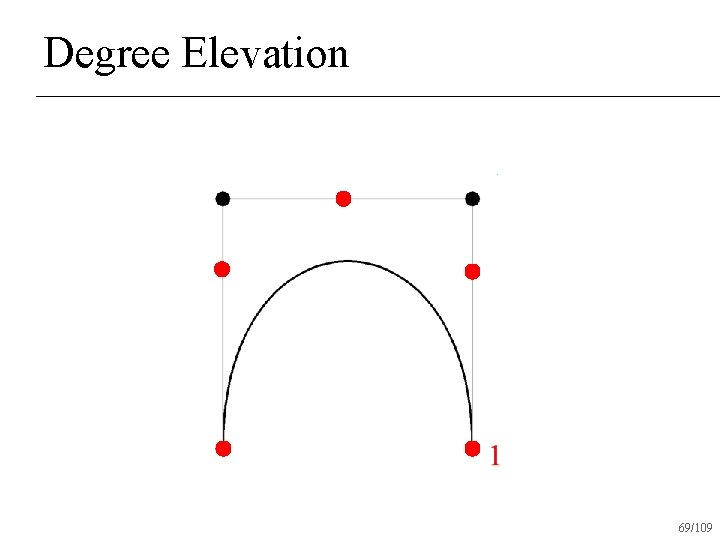
Degree Elevation 69/109
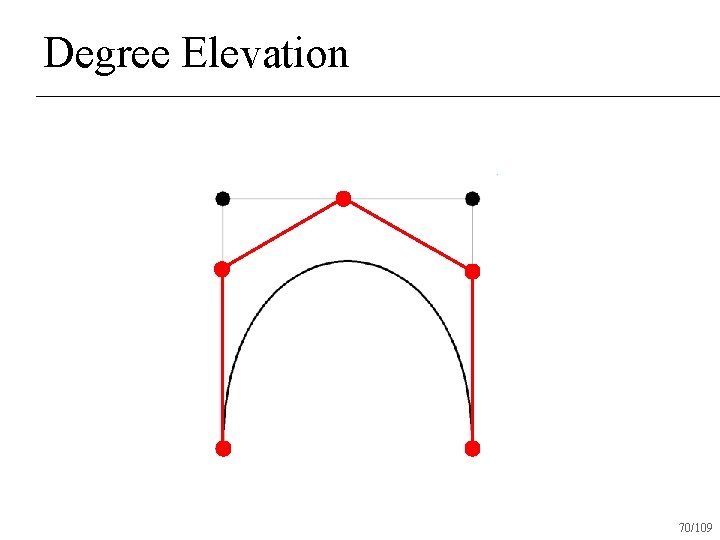
Degree Elevation 70/109

Pyramid Algorithms for Bezier Curves Polynomials aren’t pretty n Is there an easier way to evaluate the equation of a Bezier curve? n 71/109
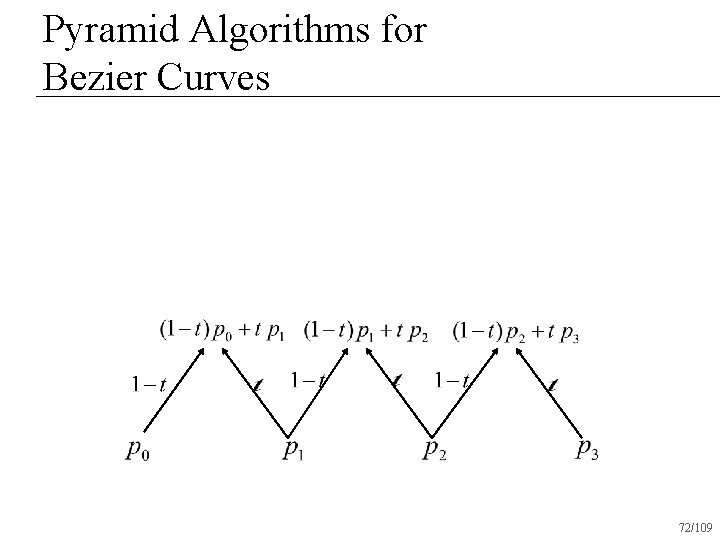
Pyramid Algorithms for Bezier Curves 72/109
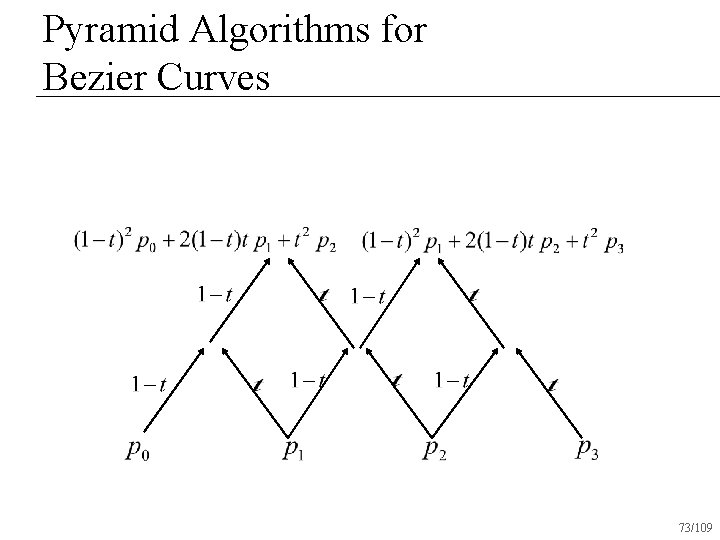
Pyramid Algorithms for Bezier Curves 73/109
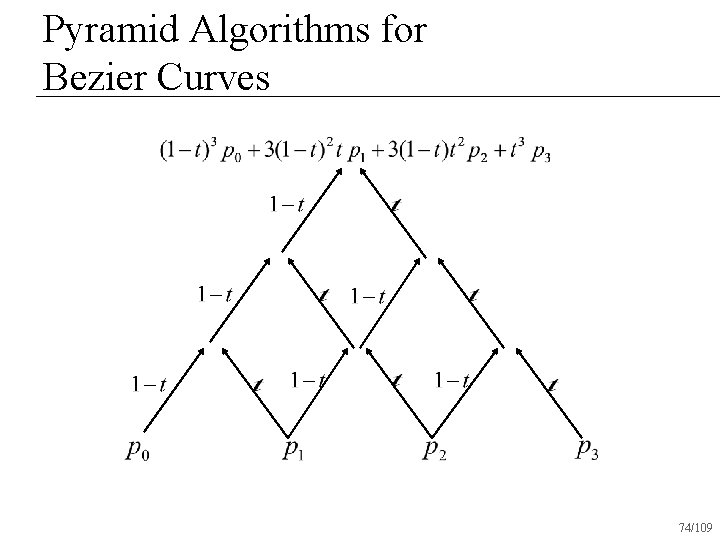
Pyramid Algorithms for Bezier Curves 74/109
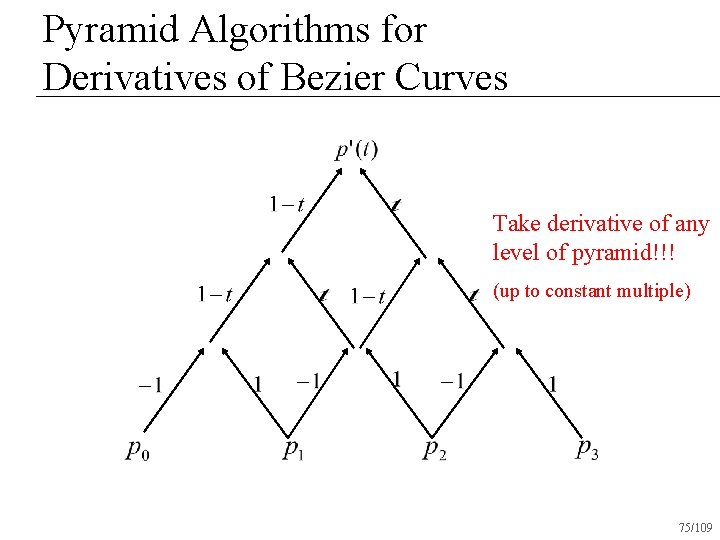
Pyramid Algorithms for Derivatives of Bezier Curves Take derivative of any level of pyramid!!! (up to constant multiple) 75/109
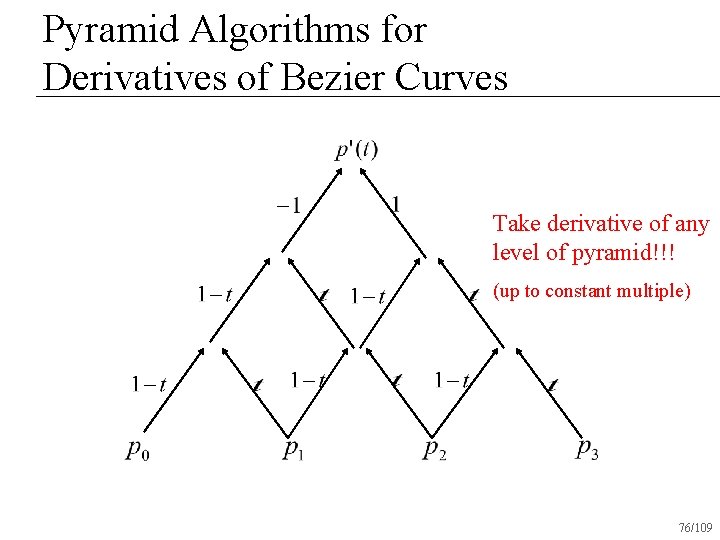
Pyramid Algorithms for Derivatives of Bezier Curves Take derivative of any level of pyramid!!! (up to constant multiple) 76/109
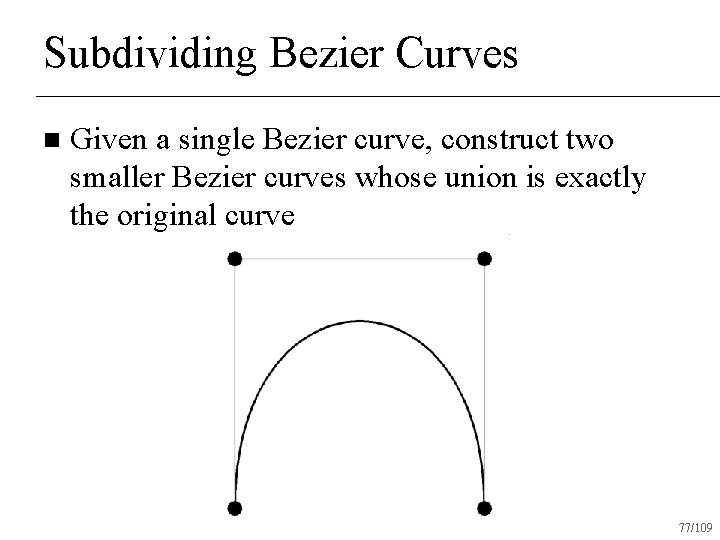
Subdividing Bezier Curves n Given a single Bezier curve, construct two smaller Bezier curves whose union is exactly the original curve 77/109
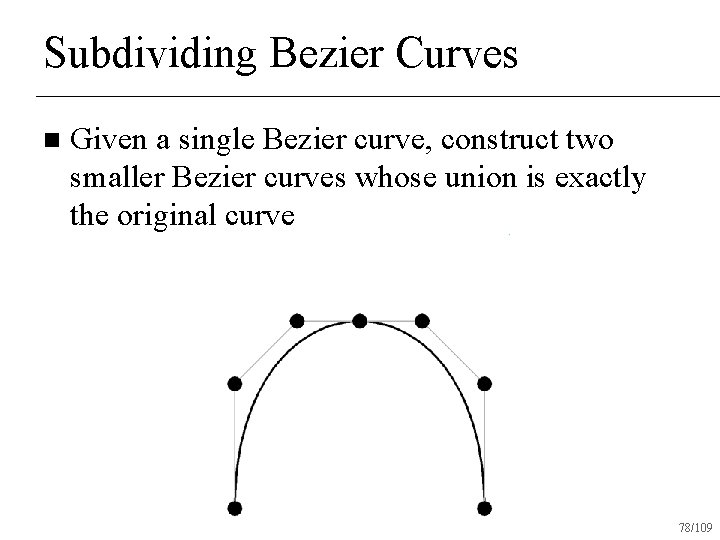
Subdividing Bezier Curves n Given a single Bezier curve, construct two smaller Bezier curves whose union is exactly the original curve 78/109
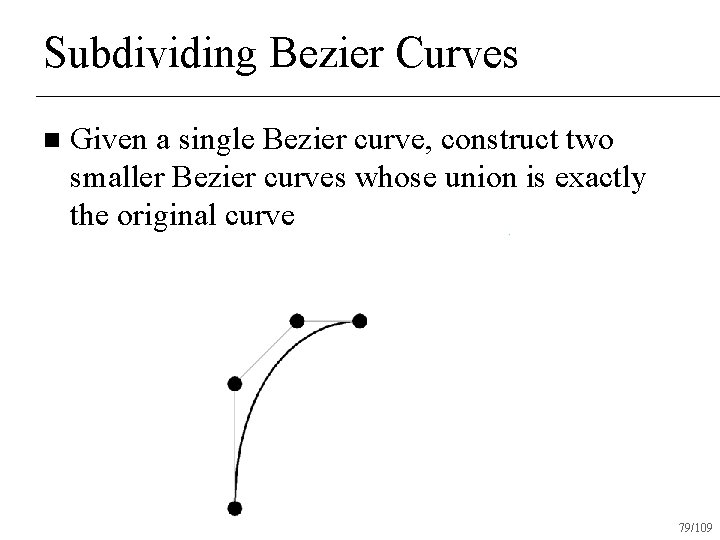
Subdividing Bezier Curves n Given a single Bezier curve, construct two smaller Bezier curves whose union is exactly the original curve 79/109
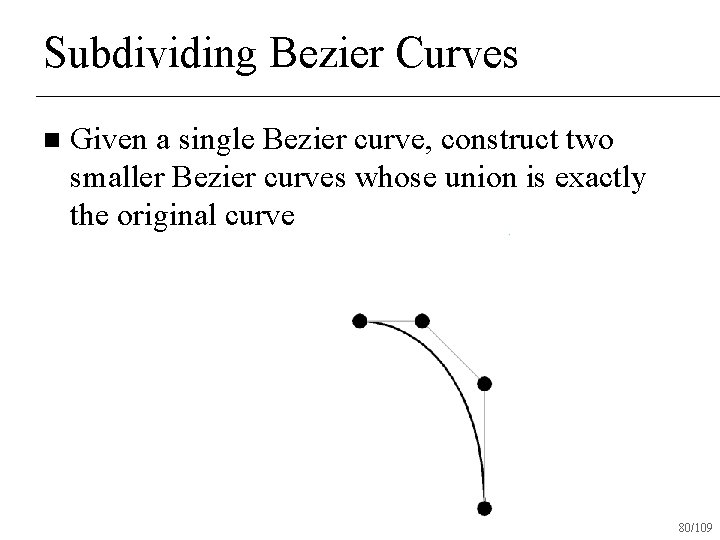
Subdividing Bezier Curves n Given a single Bezier curve, construct two smaller Bezier curves whose union is exactly the original curve 80/109
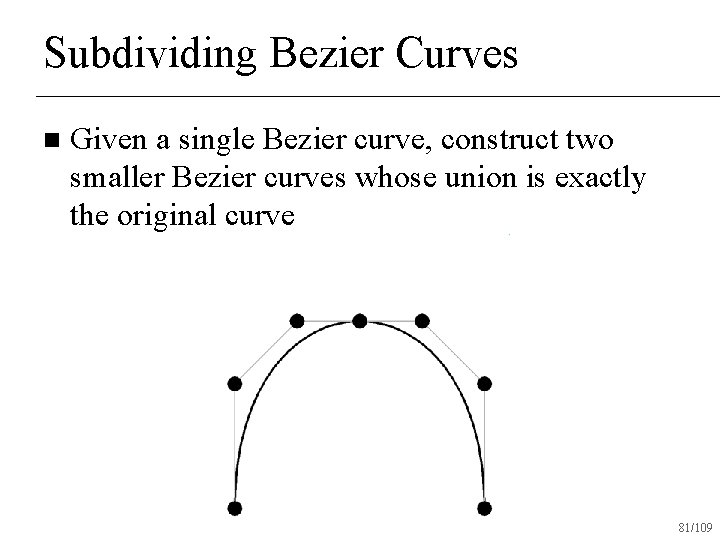
Subdividing Bezier Curves n Given a single Bezier curve, construct two smaller Bezier curves whose union is exactly the original curve 81/109
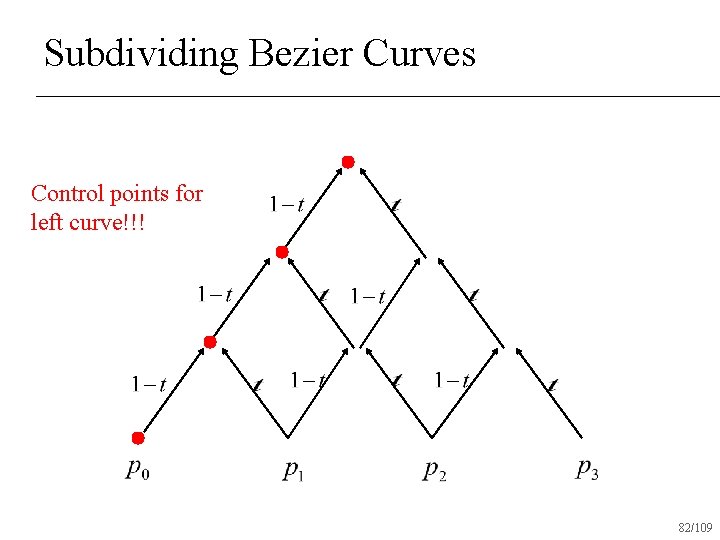
Subdividing Bezier Curves Control points for left curve!!! 82/109
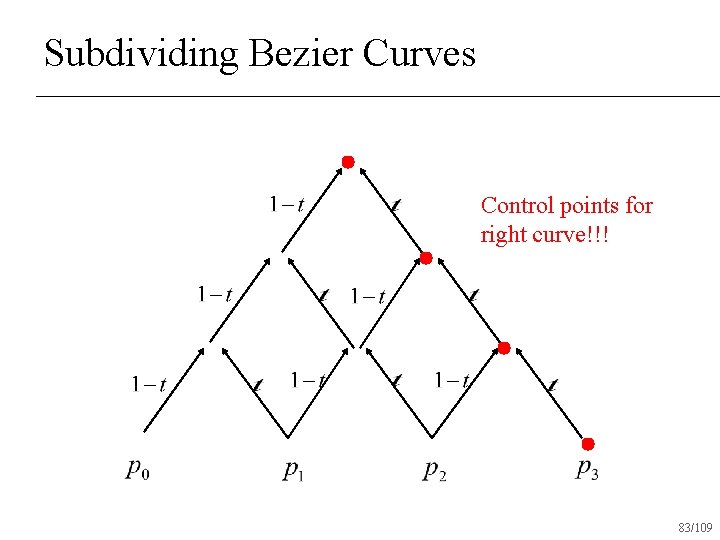
Subdividing Bezier Curves Control points for right curve!!! 83/109
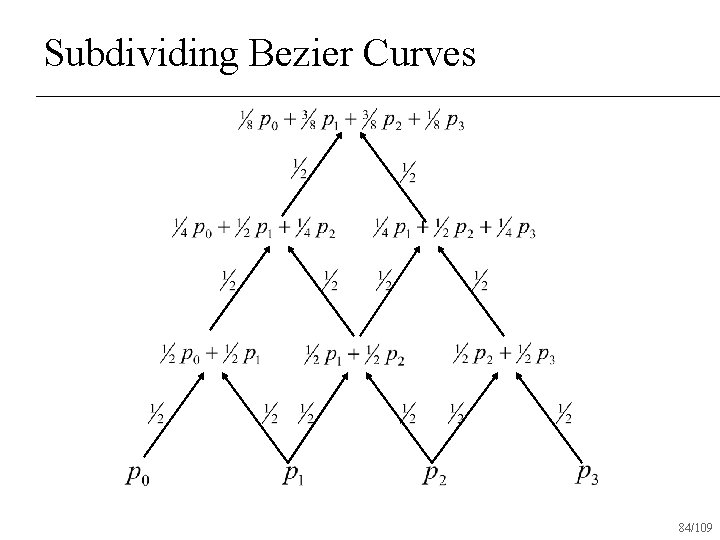
Subdividing Bezier Curves 84/109
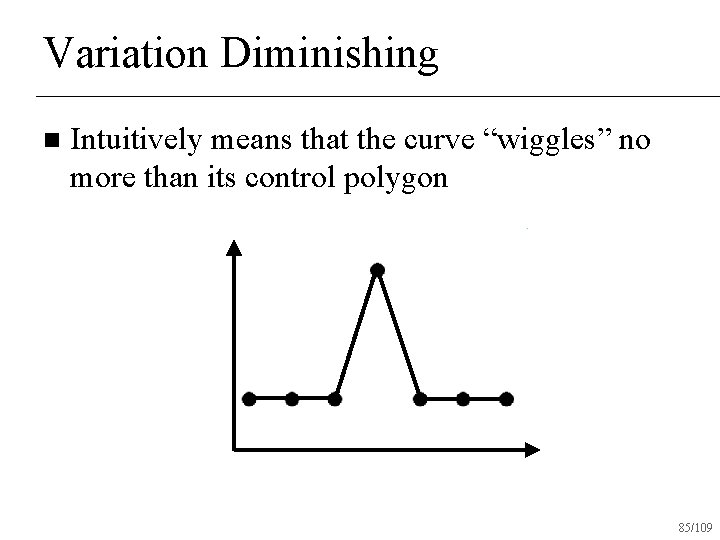
Variation Diminishing n Intuitively means that the curve “wiggles” no more than its control polygon 85/109
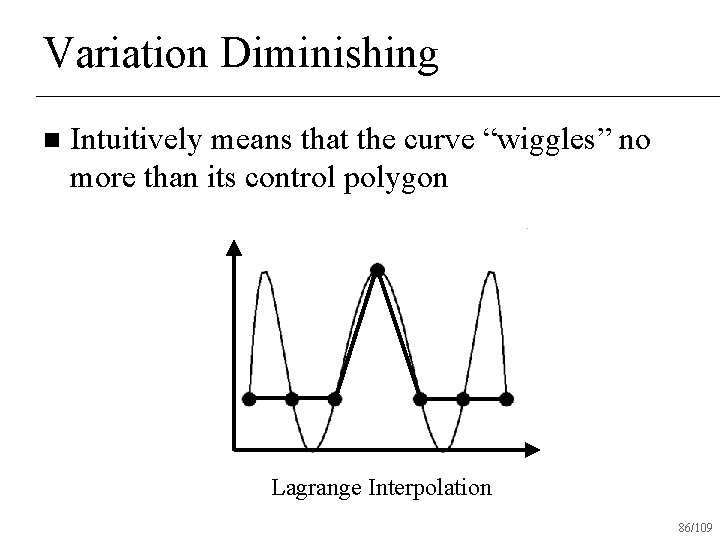
Variation Diminishing n Intuitively means that the curve “wiggles” no more than its control polygon Lagrange Interpolation 86/109
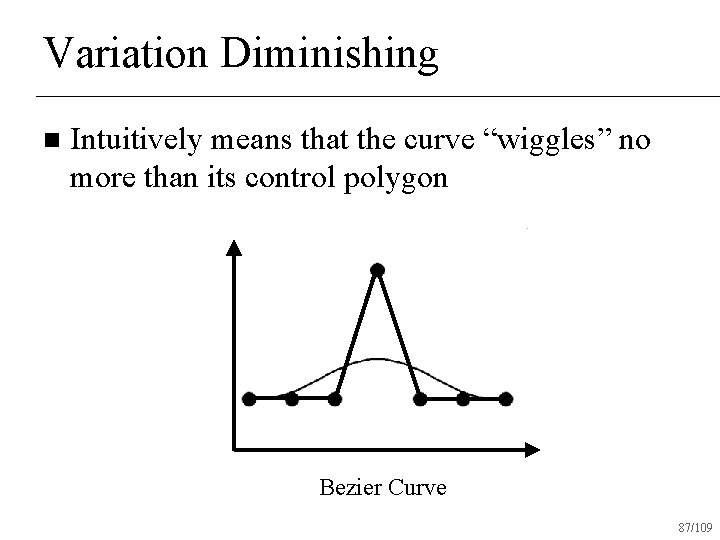
Variation Diminishing n Intuitively means that the curve “wiggles” no more than its control polygon Bezier Curve 87/109
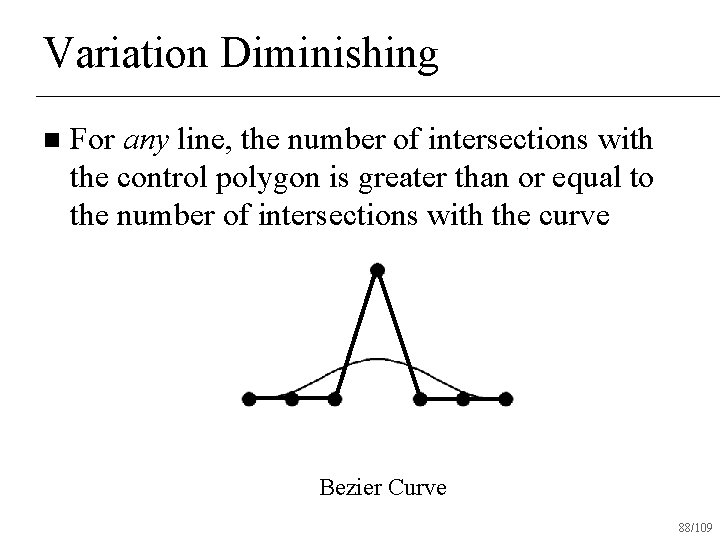
Variation Diminishing n For any line, the number of intersections with the control polygon is greater than or equal to the number of intersections with the curve Bezier Curve 88/109
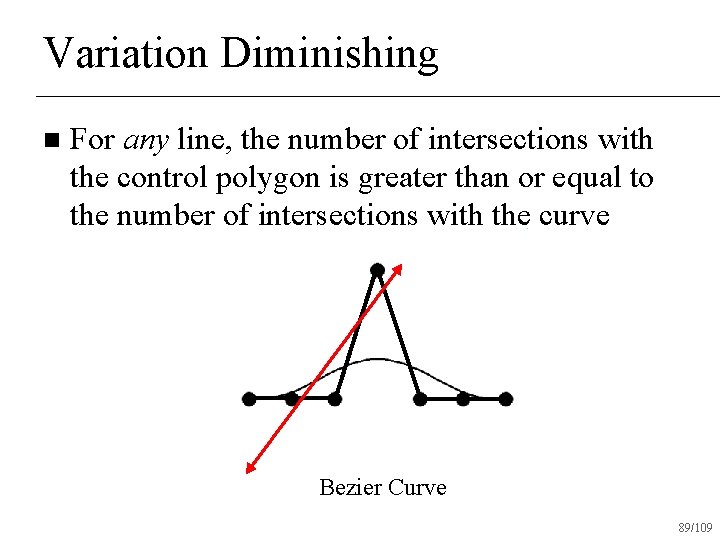
Variation Diminishing n For any line, the number of intersections with the control polygon is greater than or equal to the number of intersections with the curve Bezier Curve 89/109
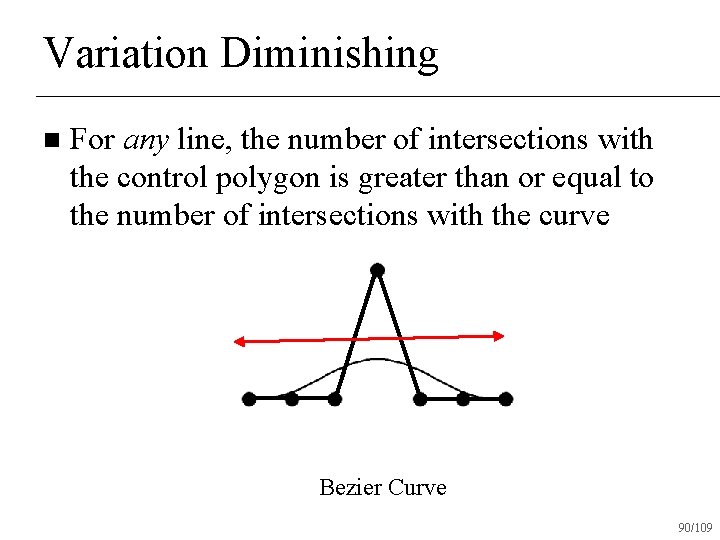
Variation Diminishing n For any line, the number of intersections with the control polygon is greater than or equal to the number of intersections with the curve Bezier Curve 90/109
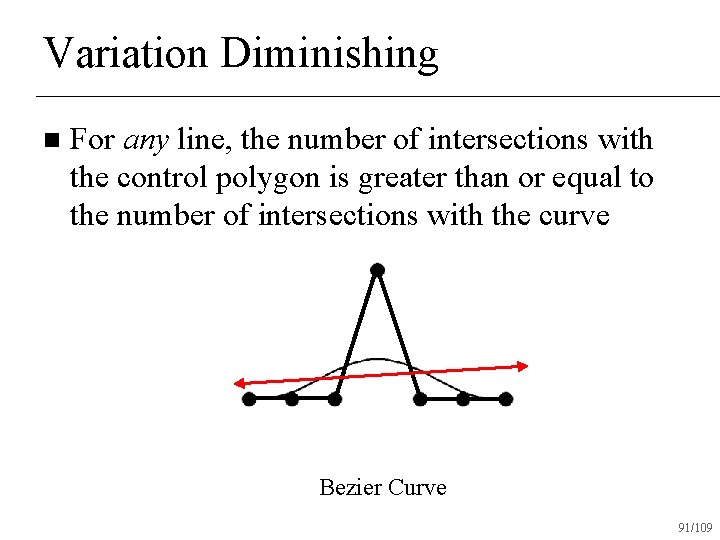
Variation Diminishing n For any line, the number of intersections with the control polygon is greater than or equal to the number of intersections with the curve Bezier Curve 91/109
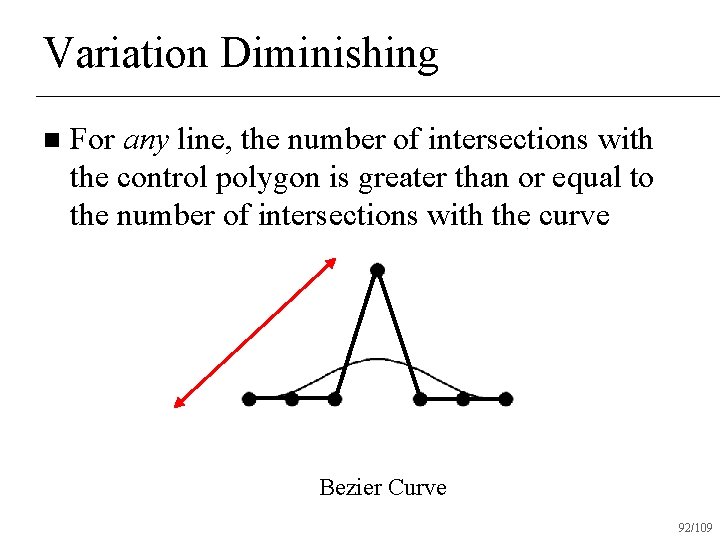
Variation Diminishing n For any line, the number of intersections with the control polygon is greater than or equal to the number of intersections with the curve Bezier Curve 92/109
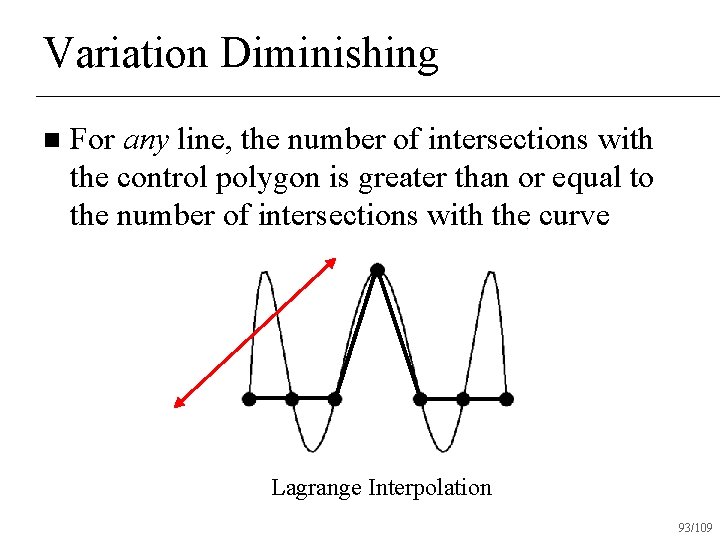
Variation Diminishing n For any line, the number of intersections with the control polygon is greater than or equal to the number of intersections with the curve Lagrange Interpolation 93/109
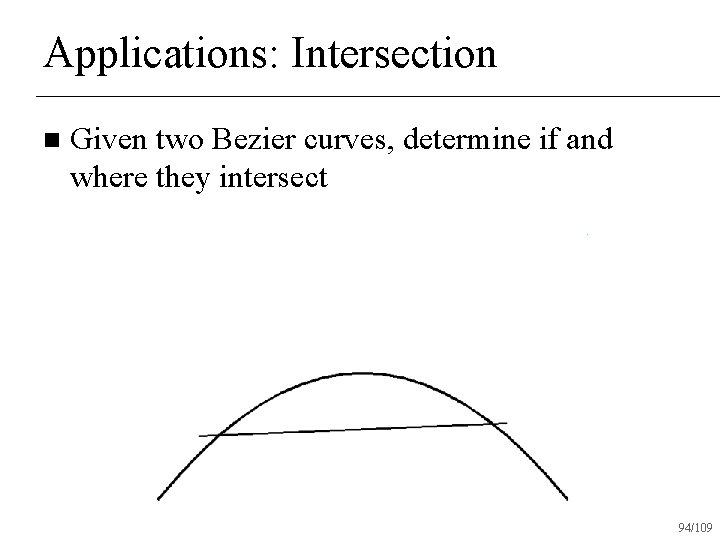
Applications: Intersection n Given two Bezier curves, determine if and where they intersect 94/109

Applications: Intersection Check if convex hulls intersect n If not, return no intersection n If both convex hulls can be approximated with a straight line, intersect lines and return intersection n Otherwise subdivide and recur on subdivided pieces n 95/109
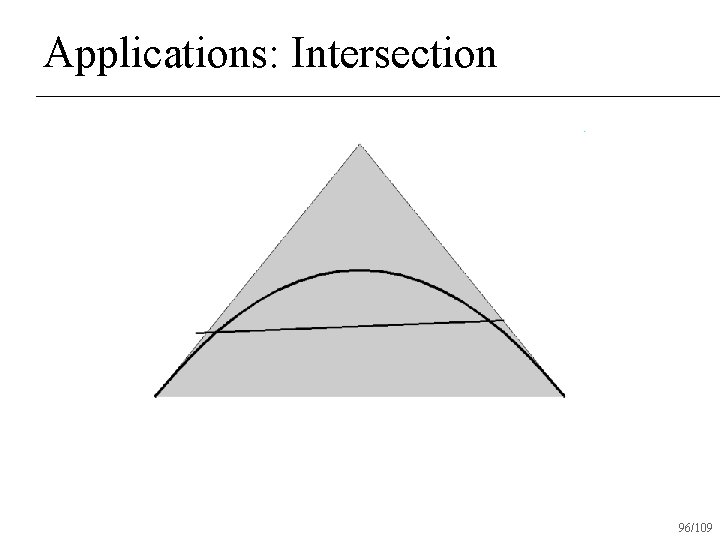
Applications: Intersection 96/109
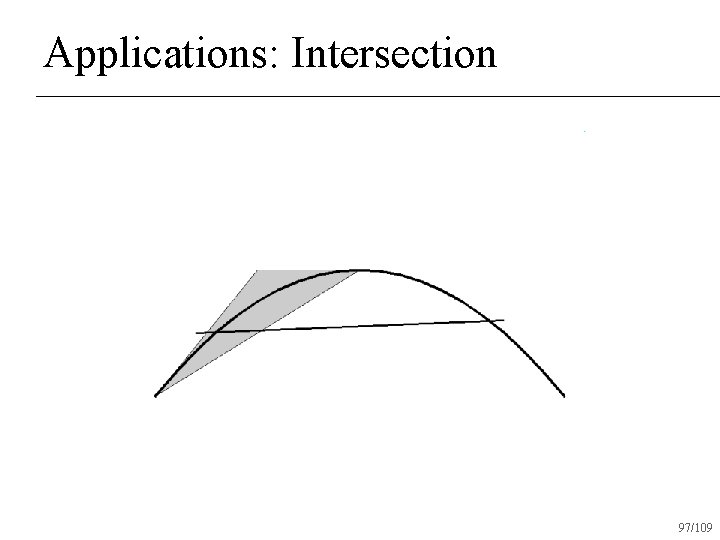
Applications: Intersection 97/109
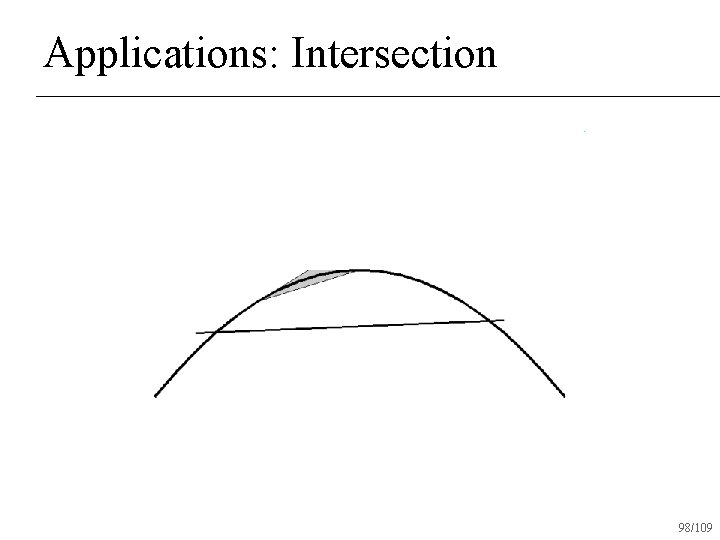
Applications: Intersection 98/109
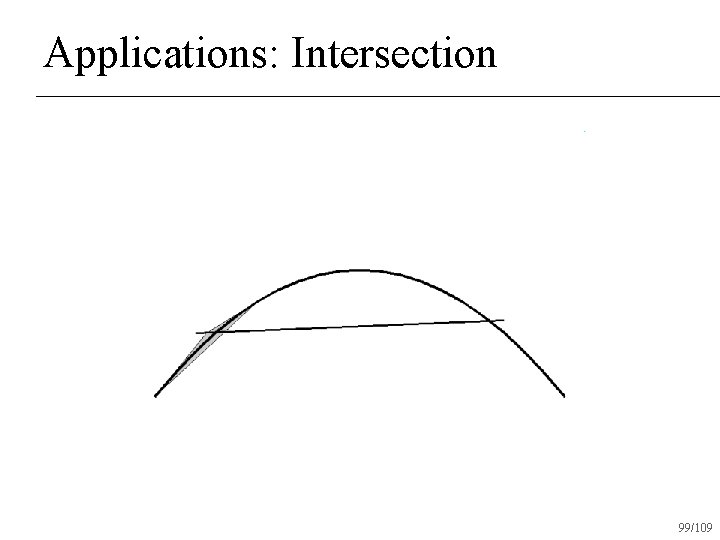
Applications: Intersection 99/109
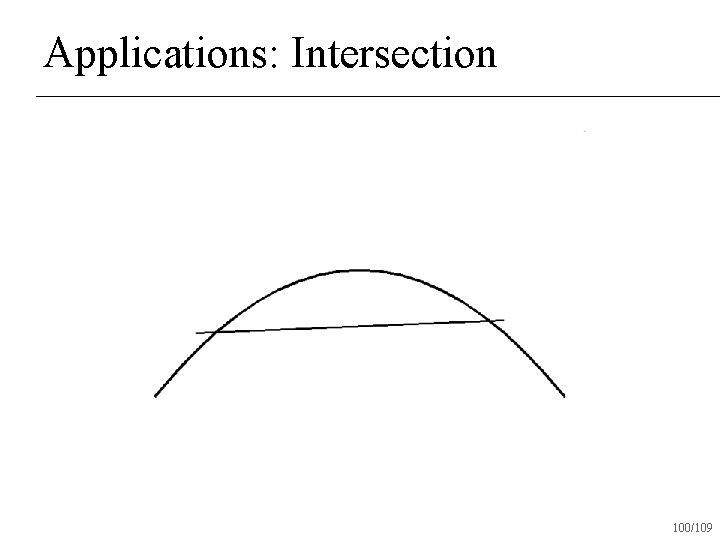
Applications: Intersection 100/109
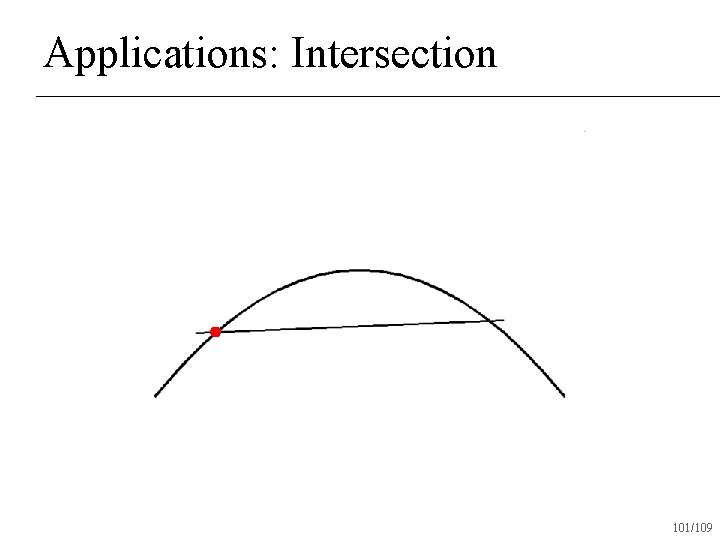
Applications: Intersection 101/109
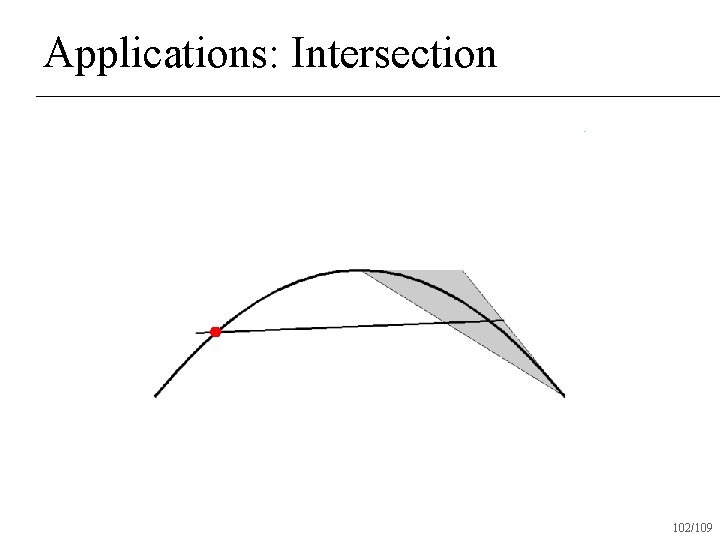
Applications: Intersection 102/109
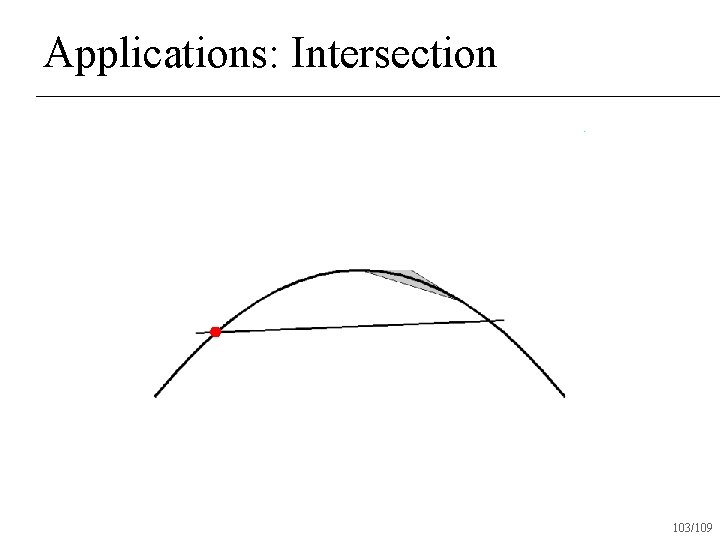
Applications: Intersection 103/109
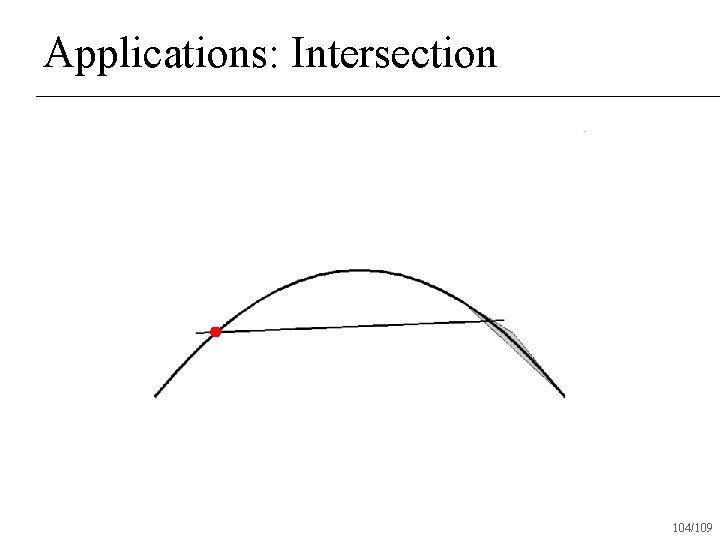
Applications: Intersection 104/109
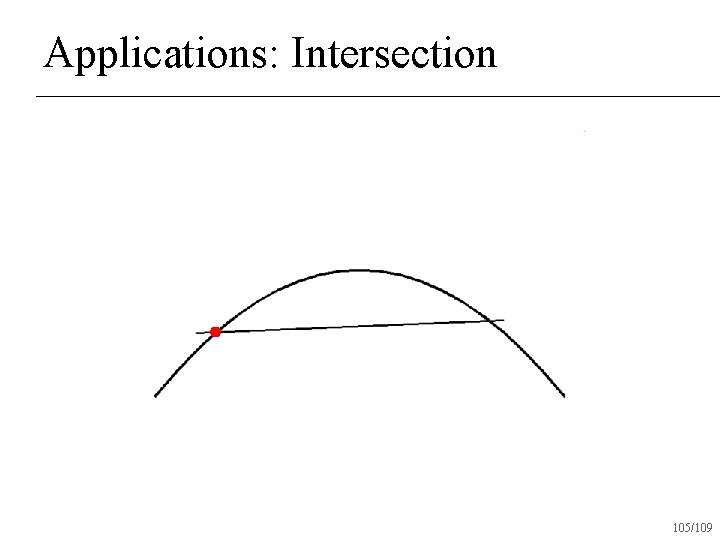
Applications: Intersection 105/109
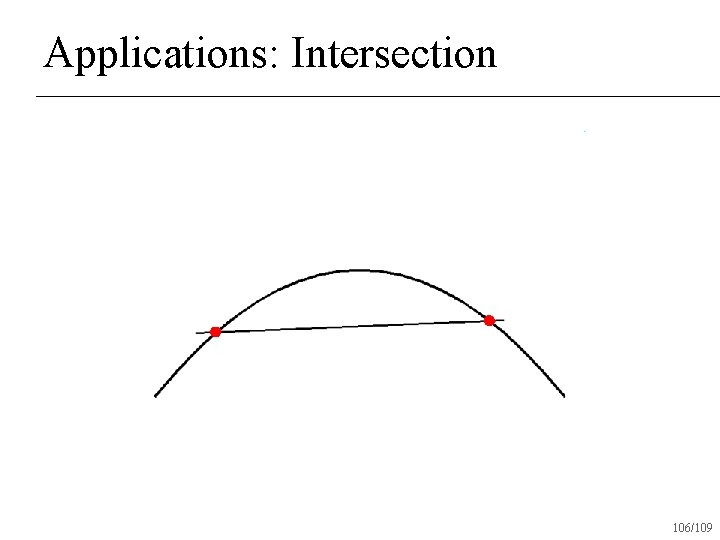
Applications: Intersection 106/109
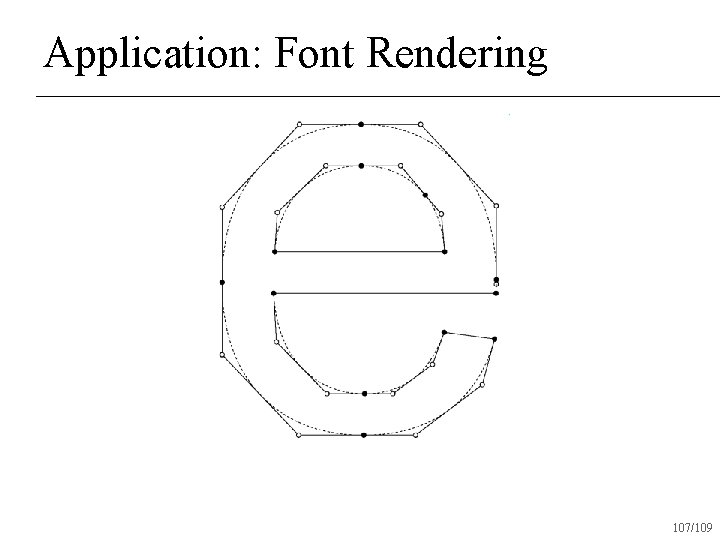
Application: Font Rendering 107/109
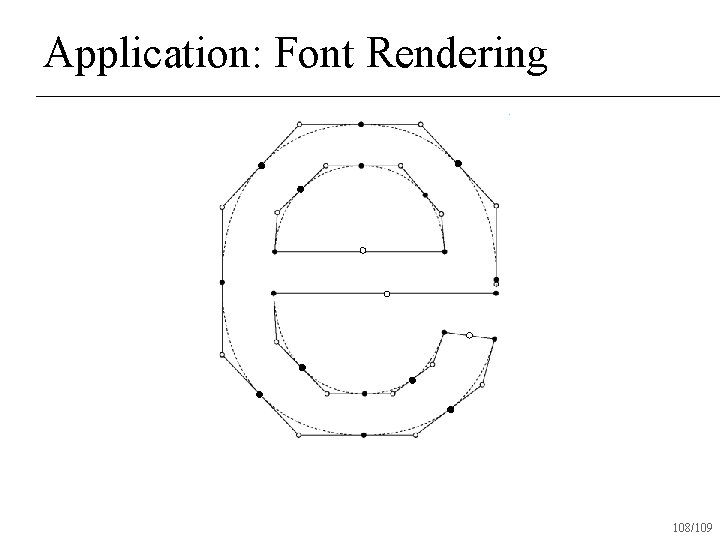
Application: Font Rendering 108/109

Application: Vector Graphics 109/109
- Slides: 109