The Basics of Counting Selected Exercises Sum Rule

The Basics of Counting: Selected Exercises

Sum Rule Example There are 3 sizes of pink shirts & 7 sizes of blue shirts. How many types of shirts are there, if a shirt type is a shirt of a particular color in a particular size? Pink Blue Copyright © Peter Cappello 2

Sum Rule A B = |A B| = |A| + |B|. A B Copyright

Sum Rule Generalization Let { S 1, S 2, …, Sn } be a partition of S. Then, | S | = | S 1 | + | S 2 | + … + | Sn |. When using the sum rule, 1. Check 1: Have I partitioned S? 1. Are the subsets pairwise disjoint? 2. Is their union equal to S? 2. Check 2: What equivalence relation corresponds to my partition? Copyright © Peter Cappello 4

Product Rule Let A be a set of elements constructed in 2 stages. • Stage 1 has n 1 possible outcomes. • For each outcome from Stage 1, Stage 2 has n 2 possible outcomes. Then, | A | = n 1 n 2. Copyright © Peter Cappello 5

Product Rule Example • A store sells pink shirts & blue shirts; each comes in small, medium, & large. • How many types of shirts are there? A shirt type can be described as an ordered pair: (color, size). Copyright © Peter Cappello 6

Product Rule: Counting Ordered Pairs Let A be a set of objects that are constructed (described) in 2 stages. • Let S be the set of values from stage 1 • Let T be the set of values from stage 2 Then, | A | = | S | x | T |. An element of A can be described as an ordered pair (a, b), where a S & b T. Copyright © Peter Cappello 7

Product Rule Example How many sequences of 2 distinct letters are there from { a, e, i, o, u } ? 1. There are 5 ways to select the 1 st letter in the sequence. 2. There are 4 ways to select the 2 nd letter in the sequence. The set of values in stage 2 depends on which letter was selected in stage 1. The size of the set of values in stage 2 does not depend on which letter was chosen in stage 1. Copyright © Peter Cappello 8

Product Rule: Counting Ordered Pairs The product rule is a special case of the sum rule: When 1. { S 1, S 2, …, Sn } is a partition of A 2. | Si | = | Sj | = m, for 1 ≤ i, j ≤ n Thus, | S 1 | + | S 2 | + … + | Sn | = n| S 1 |. The sum rule reduces to the product rule: 1. Pick the subset (n); 2. Pick the element in the subset (m) Copyright © Peter Cappello 9

Exercise 10 How many bit strings are there of length 8? Copyright © Peter

Exercise 10 How many bit strings are there of length 8? Use the product rule: Count the bit strings of length 8 by decomposing the process into 8 stages: count the possibilities for: the 1 st bit (2), the 2 nd bit (2), …, the 8 th bit (2). The product: 28 = 256 different bit strings. Copyright © Peter Cappello 11

Exercise 20 How many positive integers < 1000 1. Are divisible by 7? Copyright

Exercise 20 How many positive integers < 1000 1. Are divisible by 7? └ 999/7 ┘ = 142. 2. Are divisible by 7 & 11? . 11) = 12. 999/(7 └ ┘ 3. Are divisible by 7 but not by 11? (Use a Venn diagram) Copyright © Peter Cappello 14

Exercise 20 How many positive integers < 1000 1. Are divisible by 7? └ 999/7 ┘ = 142. 2. Are divisible by 7 & 11? . 11) = 12. 999/(7 └ ┘ 3. Are divisible by 7 but not by 11? 1. Count the # divisible by 7; 2. Subtract the # divisible by 7 & 11; └ 999/7 ┘ - └ 999/(7. 11) ┘ = 142 – 12 = 130. Copyright © Peter Cappello 15

Exercise 20 continued 4. Are divisible by 7 or 11? (Use a Venn diagram)

Exercise 20 continued 4. Are divisible by 7 or 11? We want property A or property B: use inclusion-exclusion: 1. Count the # that are divisible by 7; 2. Add the # that are divisible by 11; 3. Subtract the # that are divisible by both; └ 999/7 ┘ + └ 999/11 ┘ – └ 999/(77) ┘ = 142 + 90 – 12. 7 11 Copyright © Peter Cappello 17

Exercise 20 continued 5. Are divisible by exactly one of 7 & 11? Copyright

Exercise 20 continued 5. Are divisible by exactly one of 7 & 11? What region of the Venn diagram represents the answer? Count the symmetric difference: (union – intersection) 1. Count the # that are divisible by 7 or 11; └ 999/7 ┘ + └ 999/11 ┘ – └ 999/(7. 11) ┘ = 142 + 90 – 12 =220. 2. Subtract the # that are divisible by both; └ 999/(7. 11) ┘ = 12. 7 11 Copyright © Peter Cappello 19

Exercise 20 continued 6. Are divisible by neither 7 nor 11? What region of the Venn diagram represents the answer? 1. Count the universe (999). 2. Subtract the # that is divisible by 7 or 11 (220) giving 779. 7 11 Copyright © Peter Cappello 21

Generalize this heuristic • Given a universe U and property, P(e). • Let S = { e | e in U, P(e) } • What is |S|? • Always ask the question “Is it easier to count S = U – S? • If yes, then |S| = |U| - |S|. Copyright © Peter Cappello 22

Exercise 20 continue 7. Have distinct digits? Omit leading 0 s. For example 0

Exercise 20 continue 7. Have distinct digits? Use the sum rule to decompose the problem into counting 1. The # of 1 -digit numbers: 9 2. The # of 2 -digit numbers with distinct digits: Use the product rule: 1. Count the # of ways to select the 10 s digit: 9 2. Count the # of ways to select the unit digit: 9 3. There are 9. 9 = 81 distinct 2 -digit numbers. 3. The # of 3 -digit numbers with distinct digits: Use the product rule: 1. Count the # of ways to select the 100 s digit: 9 2. Count the # of ways to select the 10 s digit: 9 3. Count the # of ways to select the unit digit: 8 4. There are 9. 9. 8 = 648 distinct 3 -digit numbers. The overall answer is 9 + 81 + 648 = 738. Copyright © Peter Cappello 24

Alternate approach – Make a 3 -level tree of 3 -digit numbers • Top level (100 s digit): branch: 0 vs. !0 • Middle level (10 s digit): branch: 0 vs. !0 • Bottom level (1 s digit): branch: 0 vs. !0 – Add the solutions for the branches representing 3 -digit numbers with distinct digits. Copyright © Peter Cappello 25

1. 000: Invalid – out of range 2. 00 X: 9 3. 0 X 0: 9 x 1 = 9 4. 0 XY: 9 x 8 = 72 5. X 00: Invalid 6. X 0 Y: 9 x 1 x 8 = 72 7. XY 0: 9 x 8 x 1 = 72 8. XYZ: 9 x 8 x 7 = 504 Sum = 738 Copyright © Peter Cappello 26

Sara’s approach Count complement set; subtract from 999. Sum rule: • Exactly 2 digits the same: – 2 -digit numbers: 9 – 3 -digit numbers: » No “ 0”: XYY | YXY | YYX: 9 x 8 x 3 » 1 “ 0”: X 0 X | XX 0: 9 x 2 » 2 “ 0”: X 00: 9 • Exactly 3 digits the same: XXX: 9 Sum: 9 + 216 + 18 + 9 = 261; 999 – 261 = 738 Copyright © Peter Cappello 27

Exercise 30 How many strings of 8 English letters are there: a) If letters

Exercise 30 How many strings of 8 English letters are there: a) If letters can be repeated? Use product rule: (26)8 b) If no letter can be repeated? Use product rule: 26. 25. 24. 23. 22. 21. 20. 19 c) That start with X, if letters can be repeated? Copyright © Peter Cappello 30

Exercise 30 How many strings of 8 English letters are there: a) If letters can be repeated? Use product rule: (26)8 b) If no letter can be repeated? Use product rule: 26. 25. 24. 23. 22. 21. 20. 19 c) That start with X, if letters can be repeated? Use product rule: 1. (26)7 d) That start with X, if no letter can be repeated? Copyright © Peter Cappello 31

Exercise 30 How many strings of 8 English letters are there: a) If letters can be repeated? Use product rule: (26)8 b) If no letter can be repeated? Use product rule: 26. 25. 24. 23. 22. 21. 20. 19 c) That start with X, if letters can be repeated? Use product rule: 1. (26)7 d) That start with X, if no letter can be repeated? Use product rule: 1. 25. 24. 23. 22. 21. 20. 19 e) That start & end with X, if letters can be repeated? Copyright © Peter Cappello 32

Exercise 30 How many strings of 8 English letters are there: a) If letters can be repeated? Use product rule: (26)8 b) If no letter can be repeated? Use product rule: 26. 25. 24. 23. 22. 21. 20. 19 c) That start with X, if letters can be repeated? Use product rule: 1. (26)7 d) That start with X, if no letter can be repeated? Use product rule: 1. 25. 24. 23. 22. 21. 20. 19 e) That start & end with X, if letters can be repeated? Use product rule: 1. 1. (26)6 Copyright © Peter Cappello 33

Exercise 30 continued f) That start with the letters BO, if letters can be repeated? Use product rule: 1. 1. (26)6 g) That start & end with the letters BO, if letters can be repeated? Copyright © Peter Cappello 35

Exercise 30 continued f) That start with the letters BO, if letters can be repeated? Use product rule: 1. 1. (26)6 g) That start & end with the letters BO, if letters can be repeated? Use product rule: 1. 1. (26)4 h) That start or end with the letters BO, if letters can be repeated? Copyright © Peter Cappello 36

Exercise 30 continued h) That start or end with letters BO, if letters can be repeated? Use inclusion-exclusion: a) That start with the letters BO, if letters can be repeated: (26)6 b) That end with the letters BO, if letters can be repeated: (26)6 c) Subtract those that start and end with the letters BO, if letters can be repeated: (26)4 Overall answer: 2. (26)6 - (26)4 Start w/ BO End w/ BO Copyright © Peter Cappello 2011 37

Exercise 40 How many ways can a wedding photographer arrange 6 people in a row from a group of 10, where the bride & groom are among these 10, if a) The bride is in the picture? Copyright © Peter Cappello 38

Exercise 40 How many ways can a wedding photographer arrange 6 people in a row from a group of 10, where the bride & groom are among these 10, if a) The bride is in the picture? Use the product rule: a) Pick the position of the bride: 6 b) Place the remaining 5 people from left to right in the remaining positions (use the product rule to do this): 9. 8. 7. 6. 5 Overall answer is 6. 9. 8. 7. 6. 5. Copyright © Peter Cappello 39

Exercise 40 continued b) Both the bride & groom are in the picture? Copyright

Exercise 40 continued b) Both the bride & groom are in the picture? Use the product rule: a) Pick the bride’s position: 6 b) Pick the groom’s position: 5 c) Place 4 people from the remaining 8 in the remaining 4 slots, from left to right: 8. 7. 6. 5. The overall answer is 6. 5. 8. 7. 6. 5. Copyright © Peter Cappello 41

Exercise 40 continued c) Exactly 1 of the bride & groom is in the

40 continued c) Exactly 1 of the bride & groom is in the picture? (symmetric difference of what? ) 1. Pick either the bride or the groom: 2. 2. Place that person in the picture: 6. 3. Place remaining 5 from remaining 8 people: P(8, 5) = 8. 7. 6. 5. 4. The overall answer: 2. 6. ( 8. 7. 6. 5. 4) = 80, 640. Copyright © Peter Cappello 43

Exercise 50 – A variable name in C can have uppercase & lowercase letters, digits, or underscores. – The name’s 1 st character is a letter (uppercase or lowercase), or an underscore. – The name of a variable is determined by its 1 st 8 characters. How many different variables can be named in C? Copyright © Peter Cappello 44

Exercise 50 A variable name in C can have uppercase & lowercase letters, digits, or underscores. The name’s 1 st character is a letter (uppercase or lowercase), or an underscore. The name of a variable is determined by its 1 st 8 characters. How many different variables can be named in C? Use the sum rule to count the # of variable names of i characters, for i = 1, 2, …, 8. The overall answer is the sum of these numbers. Copyright © Peter Cappello 45

Exercise 50 continued Use the product rule to count the # of names of a fixed size. Let the name have i characters. 1. The # of ways to pick the 1 st character is 2. 26 + 1 = 53. 2. The # of ways to pick subsequent characters is 53 + 10. The # of ways to pick the name is 53. (63)i-1. The overall answer is Σi=[1, 8] 53. (63)i-1 ≈ 2. 1 x 1014. Copyright © Peter Cappello 46

Product Rule: Counting Ordered Pairs • Let A be a set of objects constructed (described) in 2 stages. • Let S be the set of values from stage 1. • If a S is selected in stage 1, let Ta be the set of values for stage 2. • Essentially, A = { ( a, b ) | a S and b Ta }. • To use the product rule, for all a, b S, | Ta | = | Tb |. (Illustrate S and Ta with previous examples) The product rule is a special case of the sum rule: When 1. { S 1, S 2, …, Sn } is a partition of A 2. | Si | = | Sj |, for 1 ≤ i, j ≤ n The sum rule reduces to the product rule: | S 1 | + | S 2 | + … + | Sn | = n| S 1 |. Copyright © Peter Cappello 48

Exercise 20 continue 8. Have distinct digits and are even? Copyright © Peter Cappello

Exercise 20 continue 8. Have distinct digits and are even? Easier to: 1. count the number that have distinct digits (738) 2. subtract those that are odd: 1. 1 -digit: 5 2. 2 -digit: 40 1. 5 ways to pick the unit digit 2. 8 ways to pick the 10 s digit (nonzero) 3. 3 -digit: 320 1. 5 ways to pick the unit digit 2. 8 ways to pick the 100 s digit (nonzero) 3. 8 ways to pick the 10 s digit The total that have distinct digits & are odd is 5 + 40 + 320 = 365. The overall answer is 738 – 365 = 373. Copyright © Peter Cappello 51

20 continued The hard way: Use the sum rule directly: 1. 1 -digit: 4

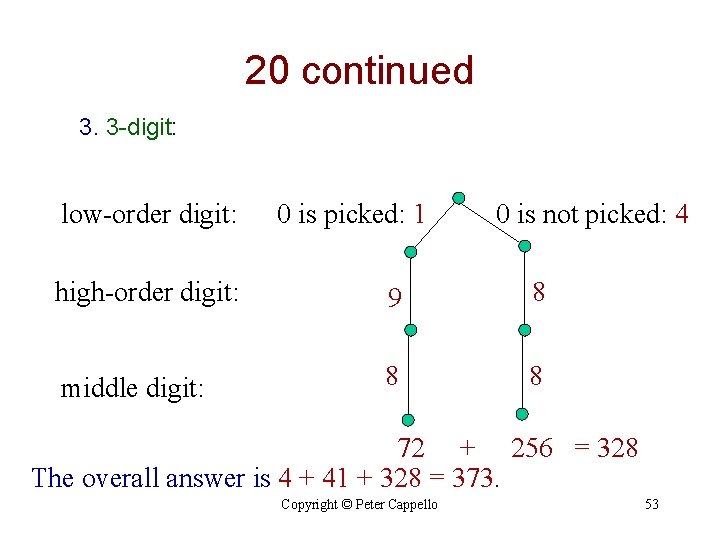
20 continued 3. 3 -digit: low-order digit: 0 is picked: 1 0 is not picked: 4 high-order digit: 9 8 middle digit: 8 8 72 + 256 = 328 The overall answer is 4 + 41 + 328 = 373. Copyright © Peter Cappello 53

40 continued c) Exactly 1 of the bride & groom is in the picture? 1. There are 6. 9. 8. 7. 6. 5 ways for the bride to be in the picture. 2. There are 6. 5. 8. 7. 6. 5. ways for the bride and groom to be in the picture. 3. The number of ways for the bride only to be in the picture is 6. 9. 8. 7. 6. 5 - 6. 5. 8. 7. 6. 5 = 6. 8. 7. 6. 5 (9 – 5) = 40, 320. 4. There are the same number of ways for the groom only to be in the picture (a 1 -to-1 correspondence between bride-only & groom-only) The overall answer is 2. 40, 320. Copyright © Peter Cappello 54

40 alternate answer for part c c) Exactly 1 of the bride & groom is in the picture? Use the product rule: 1. Pick the bride or groom to be in the picture: 2. 2. Count the number of ways to fill out that picture. Use the product rule: 1. Place the bride/groom: 6 2. Fill in the other positions from left to right: 8. 7. 6. 5. 4. The overall answer is 2. 6. 8. 7. 6. 5. 4 = 80, 640. Copyright © Peter Cappello 55