The basic question of Computer Science What is

The basic question of Computer Science What is computable? By asking this we're trying to answer the question of what computers can and cannot do. What are their strength? What are their limits? Shortest Answer: a. Have to be able to write an algorithm for the problem solution. b. Algorithm cost cannot be too large: o(logn), O(n k).

CS Concepts: Computational Power • Computational power refers to the types of problems a computer can solve. – It has nothing to do with how fast a computer is nor how nice the graphics are. • It turns out very simple computers are just as powerful than very expensive ones (although slower). • So in terms of computational power, all computers are equal. – This allows generalized solutions - solve a problem for one and we solve it for all. • Since all computers are equal, we tend to focus on types of problems rather than types of computers. – Is the problem computable?

Be able to Identify Patterns of Doubling/Halving • Consider two math operations: taking a number to a power, and taking the log of a number. • We will focus on the number 2 (binary – no surprise) n 2 n n log 2 n 0 1 2 3 … 8 9 10 1 2 4 8 … 256 512 1024 0 1 2 3 … 8 9 10

Example: Color Depth • How many colors are available if each pixel uses n bits? Bits Values Colors 1 0 1 Black White 00 01 10 11 Black Dark Gray Light Gray White 2 • Bits 3 Values Colors 000 001 010 011 100 101 110 111 Black Blue Green Yellow Red Purple Orange White How many bits are required for 256 colors? – 8 bits, because log 2 256 = 8 – That’s one byte – coincidence? ? ?

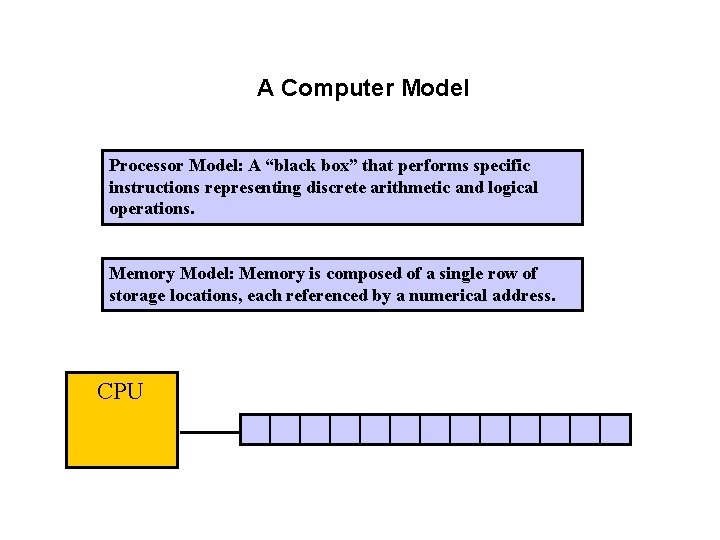
A Computer Model Processor Model: A “black box” that performs specific instructions representing discrete arithmetic and logical operations. Memory Model: Memory is composed of a single row of storage locations, each referenced by a numerical address. CPU

Algorithm Basics • Definition: A step by step procedure written so precisely that there is essentially no possibility for variation in its performance. • Written in pseudo-code – Part English, part computer code – Generic enough to be easily translated into most computer languages. • Five parts, each must be detailed: – – – • A list of inputs and their types A list of other variables and their types Initialization Computation A list of outputs and end conditions If given a simple algorithm be able to discuss it and how it operates.

Why Algorithms are Important • Algorithms have no mention of a computer. – Remember that CS focuses on the computation not the machine. – Thus, an algorithmic solution to a problem means the problem is solved for every computer – We’ll find a fast machine if we have to. • Each step in the algorithm was precise – Therefore each step can be described and measured in terms of cost. • This helps us answer the two big questions: Can it be computed and at what cost? • Lastly: Algorithms can be abstracted into functions.

4 Properties of Good Algorithms • Correctness: – The algorithm works correctly for all possible inputs. . • Precision: – The algorithm’s procedures are specified in such a way that the same actions are taken no matter who is performing it (Notice what the book says about that on p 32) • Incremental Operation: – Each step specified should consist of a single logical step. • Abstraction: – Abstraction allows for many incremental steps to be logically grouped into single step.

Example Algorithm Problems • • • What inputs are required? If the program written from this algorithm was executed with x = 12, y = 10 as input, what would the output be? Pretend the algorithm was turned into a function, foo(x, y). If used in a program like below, what is the type of "myvar? " – myvar = foo( 12, 10); Algorithm: foo(x, y) Inputs: Integer x; Number y; Others: Number z; Initialization: Assume x, y, given to us. Computation: IF ( y > x ) THEN z = y / 2; ELSE z = (x + y) / 2; ENDIF Output: return z;

Definition of Function x Add 1 x+1 Function: A function is a “black box” that takes input, operates on it, and produces output. A function is fully defined by three things: input, output, and a description relating the output to the input. Example: The Add 1 function: Input - a number, x. Output - a number, F(x) Operation - F(x) = x + 1

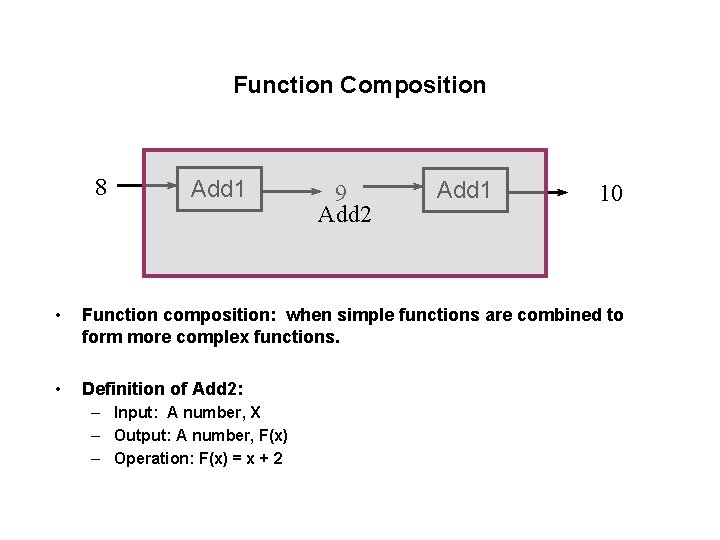
Function Composition 8 Add 1 9 Add 2 Add 1 10 • Function composition: when simple functions are combined to form more complex functions. • Definition of Add 2: – Input: A number, X – Output: A number, F(x) – Operation: F(x) = x + 2

Why are Functions Important? • Simple functions are the building blocks of all computation. – Remember our model of a Processor allows only simple operations. – Real Processors allow only simple operations. – Simple functions are easily described. • Iteration: One function repeatedly calling another. • Recursion: One function repeatedly calling itself. • We can build large programs by composing small functions. • We can describe large programs by describing the functions that make them up and how they are composed.

Functions are Abstract Algorithms • • Algorithms take in input, operate on it, and produce output. Functions take in input, operate on it, and produce output. • • When we speak of functions we focus on WHAT is being done. When we speak of algorithms we focus on HOW things are done. • Algorithms can specify how functions produce their results. – Many different algorithms may specify a single function. • Functions can be thought of as abstract algorithms. • Many algorithms can map to the same function.

Order Notation • ORDER NOTATION allows us to relate computational cost to problem size. • Most input data can have a size associated with it, like the size of a list. • Be able to compare relative sizes of different orders: – O(k) < O(log n) < O(nk) < O(kn) < O(n!)

Why Use Order Notation • The order (or cost) of a computation tells us whether it is computable or not: – All O(k) and O(n) problems are computable. – O(nk) problems are computable ( usually k = 1, 2, or 3) – O(kn) are not computable (except for very small n). • Order notation allows us to compare the efficiency of different algorithms that have been developed to solve the same problems. • Order notation allows us to compare the efficiency of our algorithms with known costs for problems. – You don’t want the cost of your algorithm to be larger than the known best costs for a problem. – You cannot make an algorithm lower than the proven best cost.

Program Control: Introduction • A list of program statements that always execute in sequence from top to bottom is called a BASIC BLOCK. – Very few interesting programs can be written using only basic blocks. • Interesting programs have the ability to react to different input data. • PROGRAM CONTROL statements allow us to change how the program behaves based on decisions made about the input data. • Two basic program control structures are: – If-Then-Else structures which act like forks in the road during program execution. The program either takes the True branch or False branch. – Do-Loops which allow the same program statements to be executed over and over in a looping style.

Program Control: If-Then -Else • The If-Then-Else structure has three parts: – – • A predicate that must evaluate to True or False Something to do when the predicate is True Something to do when the predicate is False (Note: Doing nothing counts as something to do) An example in our algorithmic pseudo-code: IF ( X > Y) THEN print(x) ELSE print(y) ENDIF • Notice: We needed a way to tell when we were done – ENDIF.

Program Control: Do-Loop • Do-Loops in Java. Script: – Each loop requires three things: an initial value, a stopping condition, and a way to change the looping variable. – The format for this is for(initial value; stop condition; increment rule) • Example: sum = 0; For ( j = 1; j < 5; j = j + 1) { sum = sum + array[j]; } • In our example: – The initial value was set by j = 1 – The stopping condition was j < 5 (so j would be 1, 2, 3, and 4) – The increment rule increased the value of j by 1 each tie through the loop ( Java. Script note: j++ is shorthand for j = j + 1)

Variables • Why use variables? It would be almost impossible to try to program by referring to the numerical addresses. – Too complicated for the human. ( “add memory location 1 and memory location 8” ) – Different machines have different memory structures. • Three things describe a variable: name, type and its structure. • The act of specifying a new variable is called declaring the variable.

Variable Scope • Scope refers to the portions of a program that may legally reference a given memory location referred to by a variable. • Global scope indicates the memory location is always accessible. • Local scope means the memory location is only available during certain portions of the program execution. – Memory reserved within functions is only available while the function is executing. – This means that variable names defined within a function may only be used while the function is executing. • If a single variable name is repeated, the memory location being accessed by using the variable name is the “most local” definition.

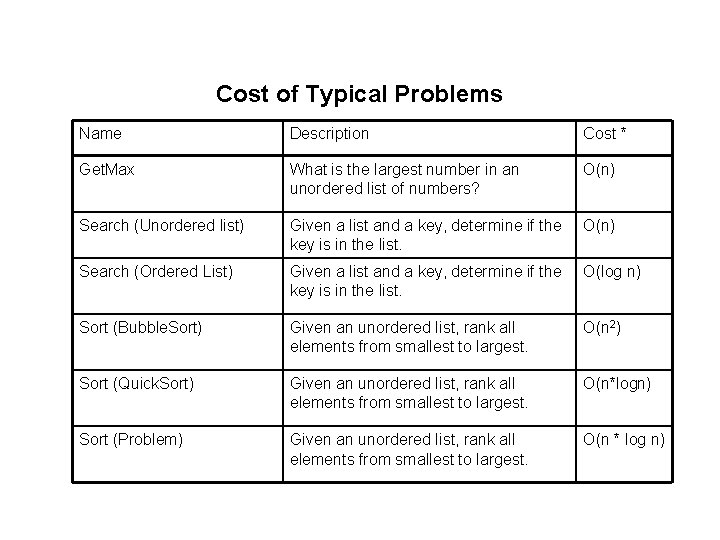
Cost of Typical Problems Name Description Cost * Get. Max What is the largest number in an unordered list of numbers? O(n) Search (Unordered list) Given a list and a key, determine if the key is in the list. O(n) Search (Ordered List) Given a list and a key, determine if the key is in the list. O(log n) Sort (Bubble. Sort) Given an unordered list, rank all elements from smallest to largest. O(n 2) Sort (Quick. Sort) Given an unordered list, rank all elements from smallest to largest. O(n*logn) Sort (Problem) Given an unordered list, rank all elements from smallest to largest. O(n * log n)