The Auction Algorithm Shahar Paz Assignment Problem Assignment

The Auction Algorithm Shahar Paz

Assignment Problem •

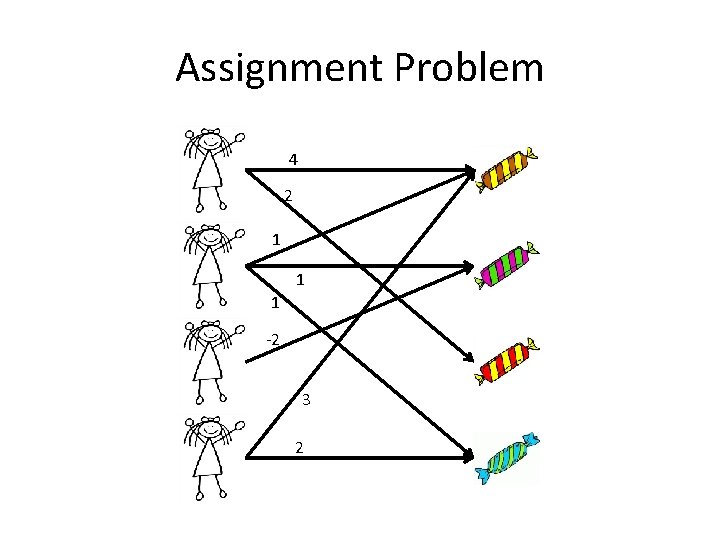
Assignment Problem 4 2 1 1 1 -2 3 2

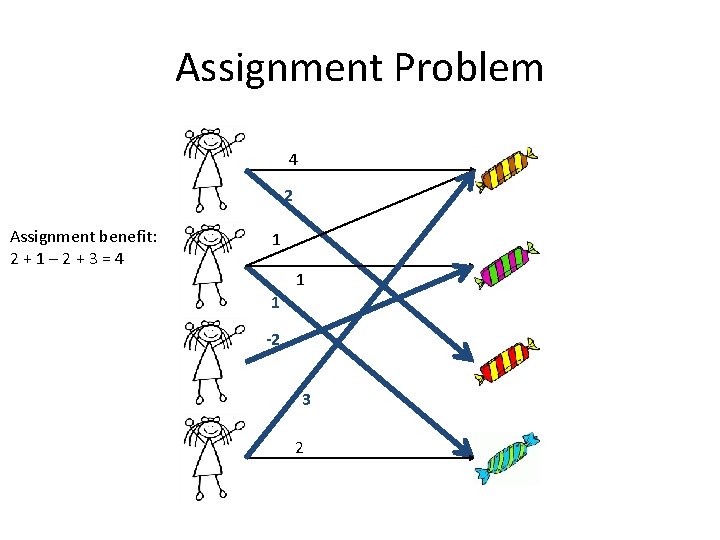
Assignment Problem 4 2 Assignment benefit: 2+1– 2+3=4 1 1 1 -2 3 2

Assignment vs. Min-Cost-Flow •

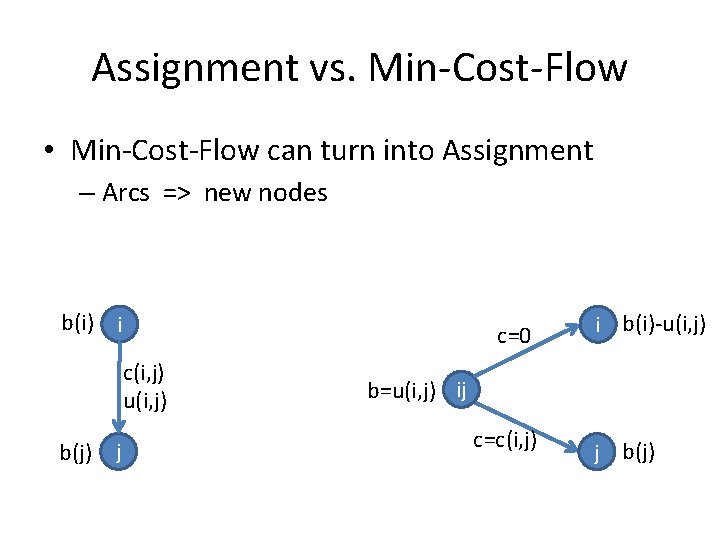
Assignment vs. Min-Cost-Flow • Min-Cost-Flow can turn into Assignment – Arcs => new nodes b(i) i c=0 c(i, j) u(i, j) b(j) j i b(i)-u(i, j) b=u(i, j) ij c=c(i, j) j b(j)

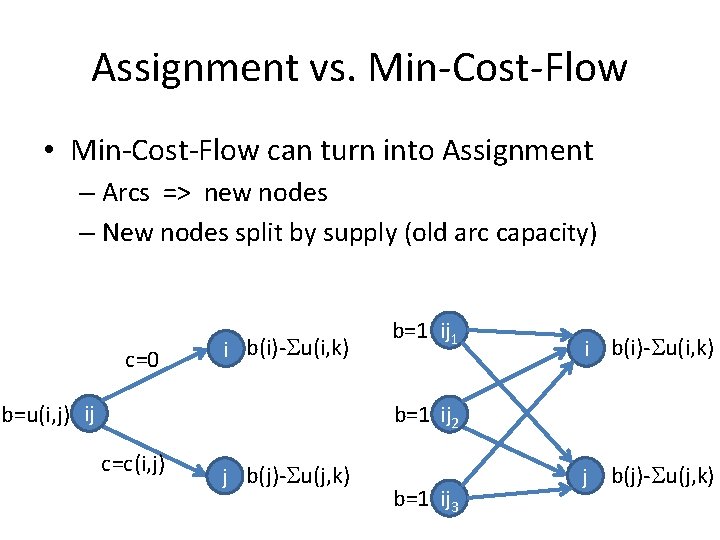
Assignment vs. Min-Cost-Flow • Min-Cost-Flow can turn into Assignment – Arcs => new nodes – New nodes split by supply (old arc capacity) c=0 i b(i)- u(i, k) b=u(i, j) ij b=1 ij 1 i b(i)- u(i, k) b=1 ij 2 c=c(i, j) j b(j)- u(j, k) b=1 ij 3 j b(j)- u(j, k)

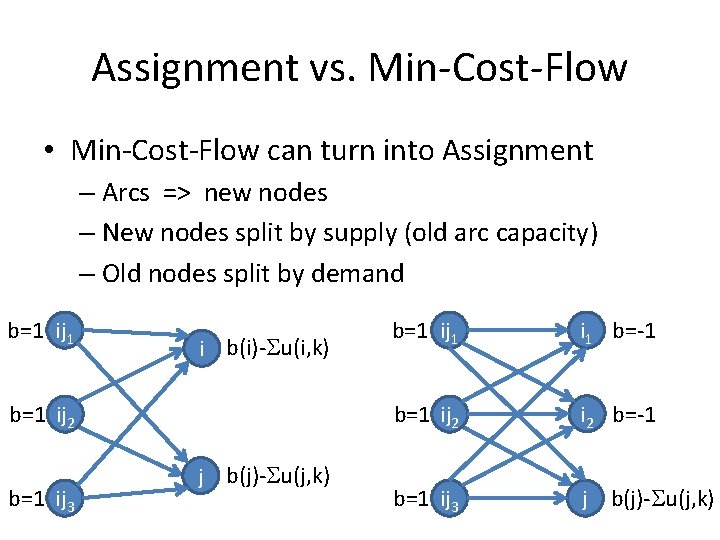
Assignment vs. Min-Cost-Flow • Min-Cost-Flow can turn into Assignment – Arcs => new nodes – New nodes split by supply (old arc capacity) – Old nodes split by demand b=1 ij 1 i b(i)- u(i, k) b=1 ij 2 b=1 ij 3 j b(j)- u(j, k) b=1 ij 1 i 1 b=-1 b=1 ij 2 i 2 b=-1 b=1 ij 3 j b(j)- u(j, k)

Assignment vs. Min-Cost-Flow •

Auction Algorithm •

Auction Termination • Observations – Objects receiving bids get assigned – Assigned objects remain assigned – Assigned persons might get unassigned – Only on termination no unassigned persons and objects