The Asymptotic Variance of Departures in Critically Loaded

The Asymptotic Variance of Departures in Critically Loaded Queues Yoni Nazarathy* EURANDOM, Eindhoven University of Technology, The Netherlands. (As of Dec 1: Swinburne University of Technology, Melbourne) Joint work with Ahmad Al-Hanbali, Michel Mandjes and Ward Whitt. MASCOS Seminar, Melbourne, July 30, 2010. *Supported by NWO-VIDI Grant 639. 072 of Erjen Lefeber

Overview • • • GI/G/1 Queue with number of served customers during Asymptotic variance: Balancing Reduces Asymptotic Variance of Outputs Main Result:

The GI/G/1/K Queue overflows Assume: Load: Squared coefficients of variation:

Variance of Outputs Asymptotic Variance Simple Examples: * Stationary stable M/M/1, D(t) is Poisson. Process( ): * Stationary M/M/1/1 with , D(t) is Renewal. Process(Erlang(2, )): Notes: * In general, for renewal process with : * The output process of most queueing systems is NOT renewal

Asymptotic Variance for (simple) After finite time, server busy forever… is approximately the same as when or

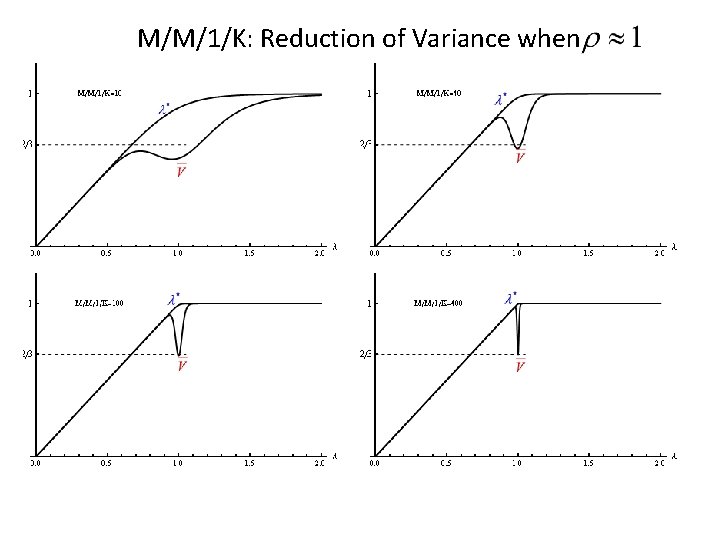
M/M/1/K: Reduction of Variance when

Summary of known BRAVO Results

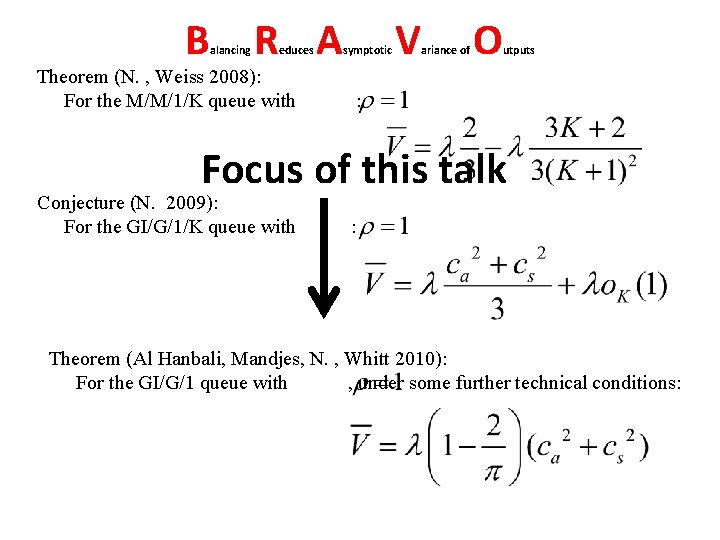
B alancing R A educes Theorem (N. , Weiss 2008): For the M/M/1/K queue with symptotic V ariance of O utputs : Focus of this talk Conjecture (N. 2009): For the GI/G/1/K queue with : Theorem (Al Hanbali, Mandjes, N. , Whitt 2010): For the GI/G/1 queue with , under some further technical conditions:

BRAVO Effect (illustration for M/M/1)

The remainder of the talks outlines the proof and conditions for: Assume GI/G/1 with finite second moments and

3 Steps for Theorem 1: Assume that then is UI, , with Theorem 2: Theorem 3: Assume finite 4’th moments, then, Q is UI under the following cases: (i) Whenever and L(. ) bounded (ii) M/G/1 (iii) GI/NWU/1 (includes GI/M/1) (iv) D/G/1 with services bounded away from 0

Proof Outline for Theorems 1, 2, 3

Theorem 1: Assume that then is UI, , with Proof: D. L. Iglehart and W. Whitt. Multiple Channel Queues in Heavy Traffic. I. Advances in Applied Probability, 2(1): 150 -177, 1970. so also, If, then,

We now show: Theorem 1 (cont. ) is UI since A(. ) is renewal is UI by assumption

Theorem 2: Proof Outline: Brownian Bridge:

Theorem 2 (cont. ) Now use (e. g. Mandjes 2007), Manipulate + use symmetry of Brownian bridge and uncondition…. Quadratic expression in u Linear expression in u Now compute the variance.

Theorem 3: Proving is UI for some cases Assume (*) After some manipulation… Now some questions: 1) What is the relation between Q’(t) and Q(t)? 2) When does (*) hold? So Q’ is UI Some answers: 1) Well known for GI/M/1: Q’(. ) and Q(. ) have the same distribution 2) For M/M/1 use Doob’s maximum inequality: Lemma: For renewal processes with finite fourth moment, (*) holds. Ideas of proof: Find related martingale, relate it to a stopped martingale, then Use Wald’s identity to look at the order of growth of the moments.

Proposition: (i) For the GI/NWU/1 case: Going beyond the GI/M/1 queue (ii) For the general GI/G/1 case: C(t) counts the number of busy cycles up to time t Question: How fast does grow? Lemma (Due to Andreas Lopker): For renewal process with Zwart 2001: For M/G/1: So, Q is UI under the following cases: (i) Whenever and L(. ) bounded (ii) M/G/1 (iii) GI/NWU/1 (includes GI/M/1) (iv) D/G/1 with services bounded away from 0

Summary • Critically loaded GI/G/1 Queue: • UI of in critical case is challenging • Many open questions related to BRAVO, both technical and practical

References • Yoni Nazarathy and Gideon Weiss, The asymptotic variance rate of the output process of finite capacity birth-death queues. Queueing Systems, 59(2): 135 -156, 2008. • Yoni Nazarathy, 2009, The variance of departure processes: Puzzling behavior and open problems. Preprint, EURANDOM Technical Report Series, 2009 -045. • Ahmad Al-Hanbali, Michel Mandjes, Yoni Nazarathy and Ward Whitt. Preprint. The asymptotic variance of departures in critically loaded queues. Preprint, EURANDOM Technical Report Series, 2010 -001.