The Area Question and the Integral Lesson 6

The Area Question and the Integral Lesson 6. 1

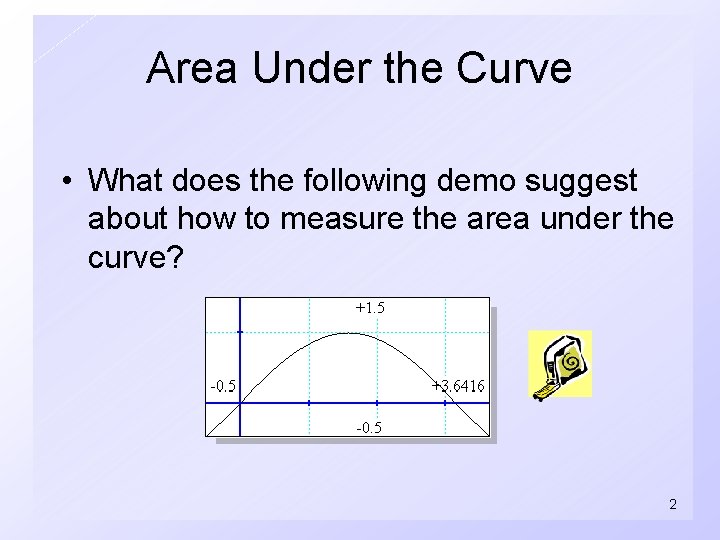
Area Under the Curve • What does the following demo suggest about how to measure the area under the curve? 2

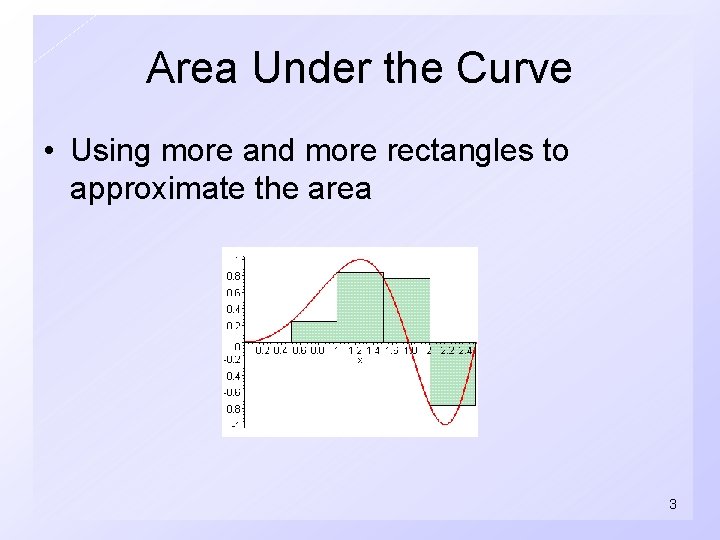
Area Under the Curve • Using more and more rectangles to approximate the area 3

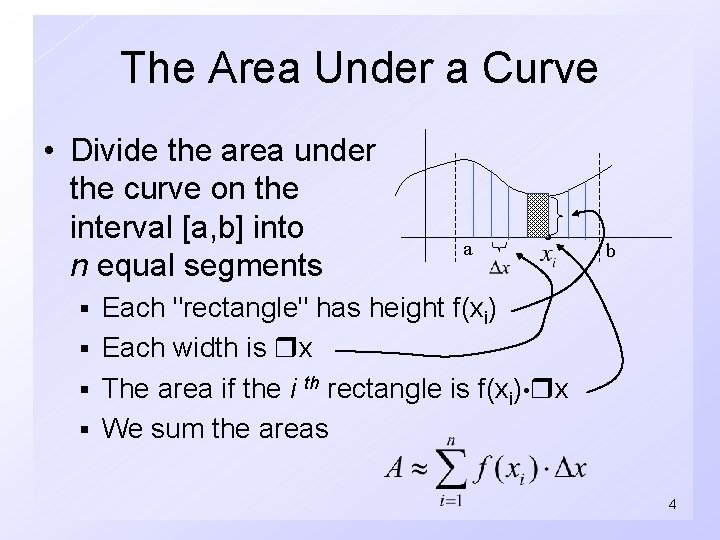
The Area Under a Curve • Divide the area under the curve on the interval [a, b] into n equal segments a • b Each "rectangle" has height f(xi) § Each width is x § The area if the i th rectangle is f(xi) • x § We sum the areas § 4

Summation Notation • We use summation notation • Note the basic rules and formulas § Summation Formulas, pg 218

Use of Calculator • Note again summation capability of calculator • Syntax is: (expression, variable, low, high)

Practice Summation • Try these

Limit of a Sum • For a function f(x), the area under the curve a b from a to b is where x = (b – a)/n and • Consider the region bounded by f(x) = x 2 the axes, and the lines x = 2 and x = 3

Limit of a Sum • Now • So

Limit of a Sum • Continuing …

Practice Summation • For our general formula: • let f(x) = 3 – 2 x on [0, 1]

The Sum Calculated • Consider the function 2 x 2 – 7 x + 5 • Use x = 0. 1 • Let the = left edge of each subinterval • Note the sum 12

The Area Under a Curve • The accuracy of the summation will increase if we have more segments § As we increase n • As n gets infinitely large the summation is exact 13

The Definite Integral • We will use another notation to represent the limit of the summation Upper limit of integration Lower limit of integration The integrand 14

Example • Try • Use summation on calculator. 15

Example • Note increased accuracy with smaller x 16

Limit of the Sum • The definite integral limit of the sum. is the 17

Practice • Try this • What is the summation? • Which gives us • Now take limit 18

Practice • Try this one § What is x? § What is the summation? • For n = 50? • Now take limit 19

Assignment • Lesson 6. 1 • Page 221 • Exercises 1 – 17 odd 20