The application of interference fits for overcoming limitations



















- Slides: 26

The application of interference fits for overcoming limitations in clamping methodologies for cryo-cooling first crystal configurations in X Ray monochromators Ph. D program Prof Michael Ward Dr Pete Docker Mr Josh Stimson

The Diamond Light Source

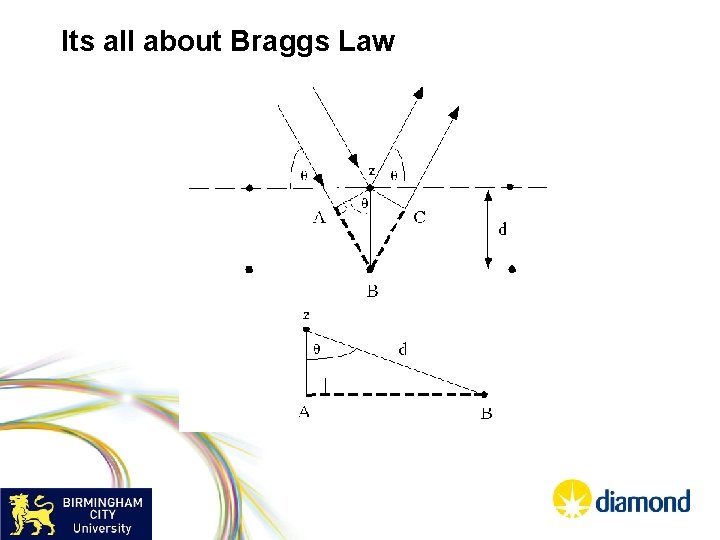
Its all about Braggs Law

The Project • Collaboration between Diamond and BCU • 3 year program • Review current and blue sky approaches using COMSOL FEA • Testing of assumptions and configurations of the world’s synchrotron monochromators • To gain a better understanding of crystal mounting and cooling considerations

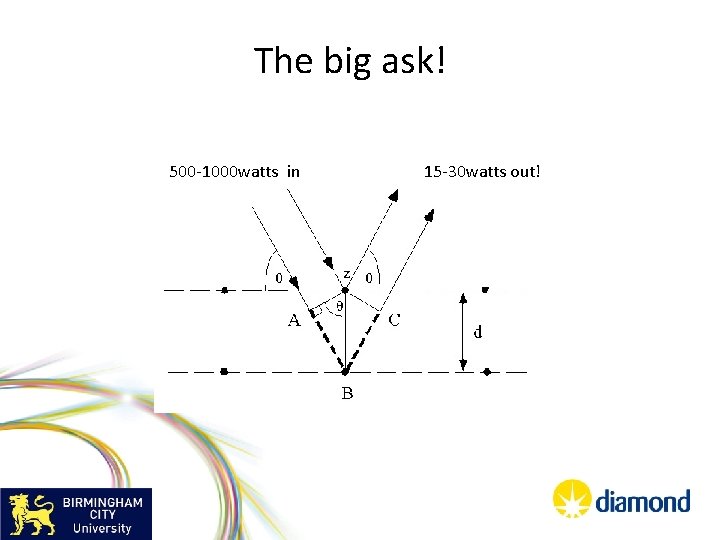
The big ask! 500 -1000 watts in 15 -30 watts out!

Different Energies Different foot prints are illuminated for different energies BUT same power! Same cooling configuration for both! Oh and allowable radius of curvature is 40 miles!

Current Approaches ‘Direct’ v ‘Indirect’ cooling Both have their merits and shortfalls

Direct Cooling The conundrum: Too much clamping – mechanical distortion Not clamping enough – thermal distortion Macro tools for sub-micron Accuracy

Concerns Is it repeatable. . . . Can a configuration be systematically repeated. Ultimately can it meet the growing power requirements in terms of cooling ability

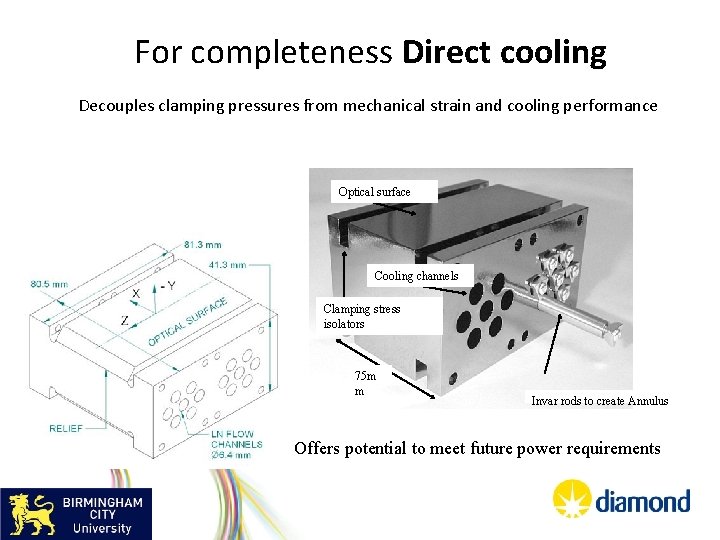
For completeness Direct cooling Decouples clamping pressures from mechanical strain and cooling performance Optical surface Cooling channels Clamping stress isolators 75 m m Invar rods to create Annulus Offers potential to meet future power requirements

Thermal Conductivity 30000 5000 20000 4500 Thermal Conductivity W/m-k 25000 10000 5000 0 0 50 Sil. . . 4000 3500 . . . 3000 2500 2000 1500 1000 500 100 0 0 150 Temperature in Kelvin 50 100 250 150 200 Temperature Kelvin 300 250 300

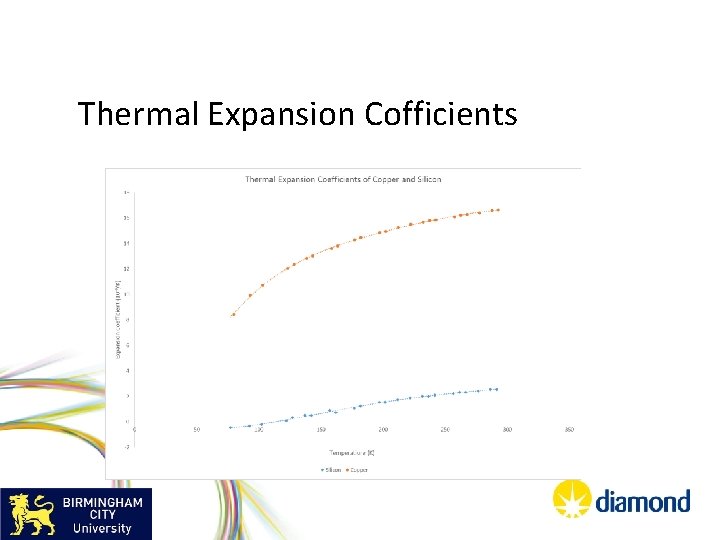
Thermal Expansion Cofficients

Reliance on pressure for cooling performance

Our Thoughts Help!

An idea!

Interference fit At RT heat copper heat exchanger and cool BUT CU shrinks much more than Si when cryo cooled so no need!

An interference fit first crystal design for a monochromator

Fit as a criteria for pressure on crystal with temperature

Three Key Considerations Room temperature gap Difference in Coef. thermal expansion Ultimate Compressive Stress Force of Linear Expansion ˃ Friction Si 700 MPa Cu 358 MPa Flatter Diffraction Plain

FEA boundary conditions Copper and silicon interference fit model with a 60 μm gap at room temperature. a) Mechanical boundary conditions, left to right: Prescribed displacement (z = 0); Prescribed displacement (x & y = 0). b) Thermal boundary conditions, left to right: Power source (10 W); Fixed temperature (80 K); Diffuse surface (to 88 K).

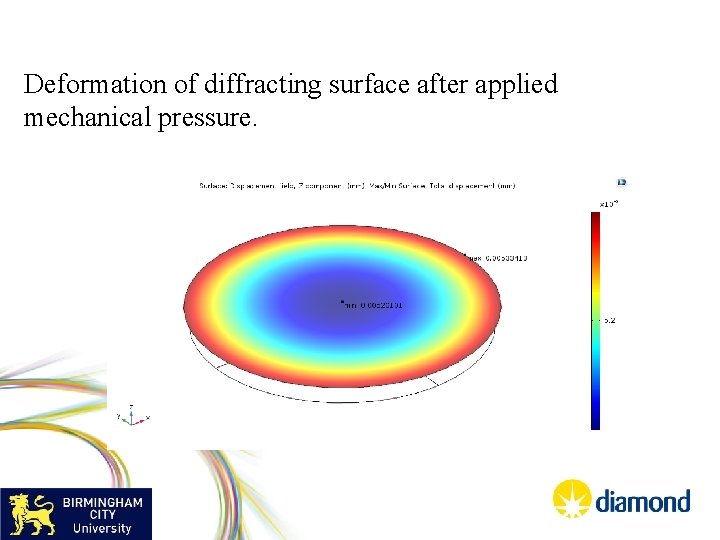
Deformation of diffracting surface after applied mechanical pressure.

Standard Configuration a) Mechanical boundary conditions, left to right: Fixed constraint; Prescribed displacement (z = 0); Pretensioned bolts (190 N). b) Thermal boundary conditions, left to right: Fixed temperature (80 K); Diffuse surface (to 88 K).

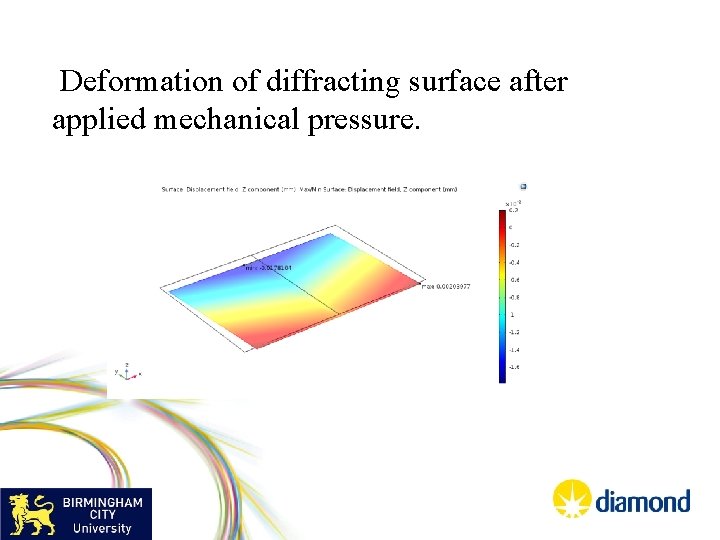
Deformation of diffracting surface after applied mechanical pressure.

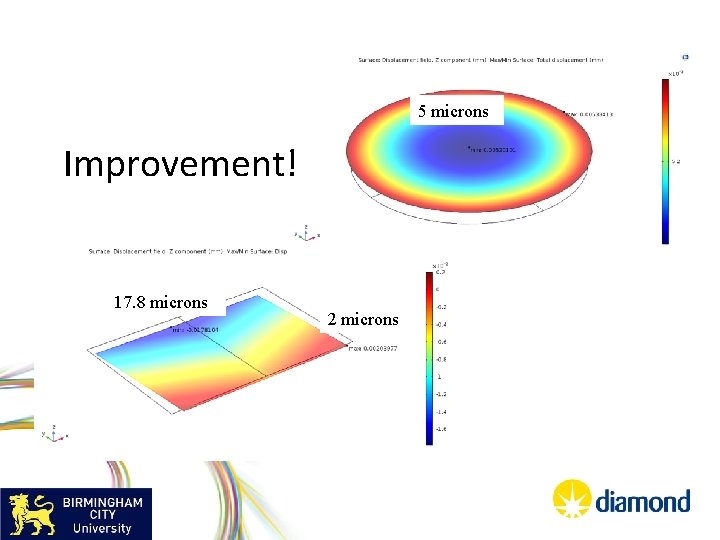
5 microns Improvement! 17. 8 microns 2 microns

Conclusions Its a win!!!! A repeatable win!!!

THANK YOU!!!!!!!