The Application of Artificial Neural Networks in Engineering

The Application of Artificial Neural Networks in Engineering and Finance Nicholas Christakis Department of Physics University of Crete DCABES, October 2009

Joint work with: Vasileios Barbaris Agis Spentzos DCABES, October 2009

Presentation Outline • Basics of Artificial Neural Networks (ANNs) • Application of ANN in rotorcraft aerodynamics • Application of ANN in the prediction of stocks prices – short-term trading DCABES, October 2009

Presentation Outline • Basics of Artificial Neural Networks (ANNs) • Application of ANN in rotorcraft aerodynamics • Application of ANN in the prediction of stocks prices – short-term trading DCABES, October 2009

Presentation Outline • Basics of Artificial Neural Networks (ANNs) • Application of ANN in rotorcraft aerodynamics • Application of ANN in the prediction of stock prices –short -term trading DCABES, October 2009

Basics of ANNs DCABES, October 2009

Basics of ANNs • ANNs: Information processing machines, inspired by the way biological nervous systems work. • ANNs composed of: – Simple processing elements (neurons) – Connected together – working in unison to solve specific problems. • ANNs – learn by example and generalize well on unseen data. – detect trends that are too complex to be noticed by either humans or other computer techniques. – deal well with situations where the inputs are erroneous, incomplete or fuzzy. DCABES, October 2009

Basics of ANNs Comparisons between Biological and Artificial Networks • Human brain – 100 109 neurons with 1000 connection paths (dendrites) per neuron 100 1012 interconnections / sec – All work in parallel 100 1012 computations/sec • Serial computer – 107 computations / sec Human brain 10 106 times faster than a serial computer DCABES, October 2009

Basics of ANNs may be used as: – Autonomous predictive tools – Pre-processors for numerical process models in order to determine unknown parameters from data sets. DCABES, October 2009

Basics of ANNs Generic Operation of ANNs Ø Train the network with a given dataset to recognize patterns within it Ø Decide after how many epochs (full cycles through the whole of the dataset) the network is adequately trained Ø Network is operational for predicting (from a given set of inputs) outputs it has not been trained for Main ANN characteristics Ø Network Architecture (how the network is set up) Ø Learning Algorithm (how the network learns) DCABES, October 2009

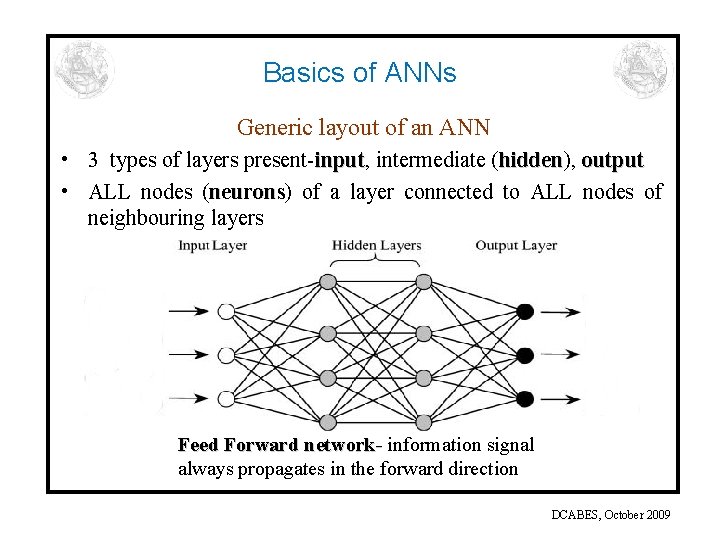
Basics of ANNs Generic layout of an ANN • 3 types of layers present-input, input intermediate (hidden), hidden output • ALL nodes (neurons) neurons of a layer connected to ALL nodes of neighbouring layers Feed Forward network- information signal always propagates in the forward direction DCABES, October 2009

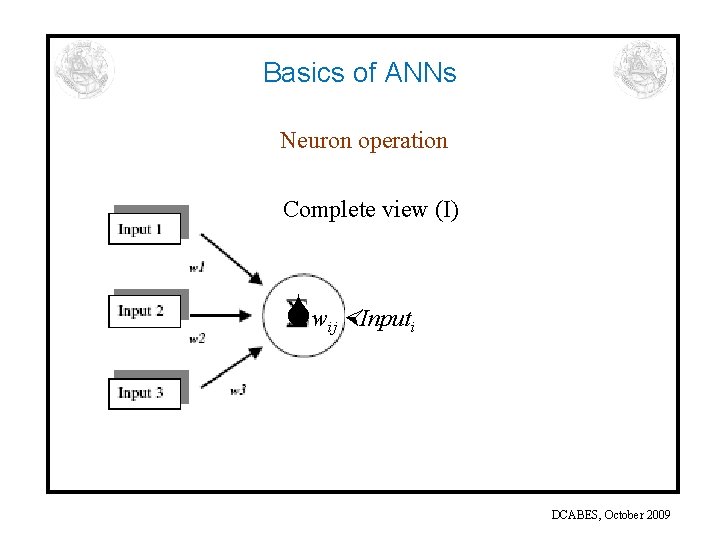
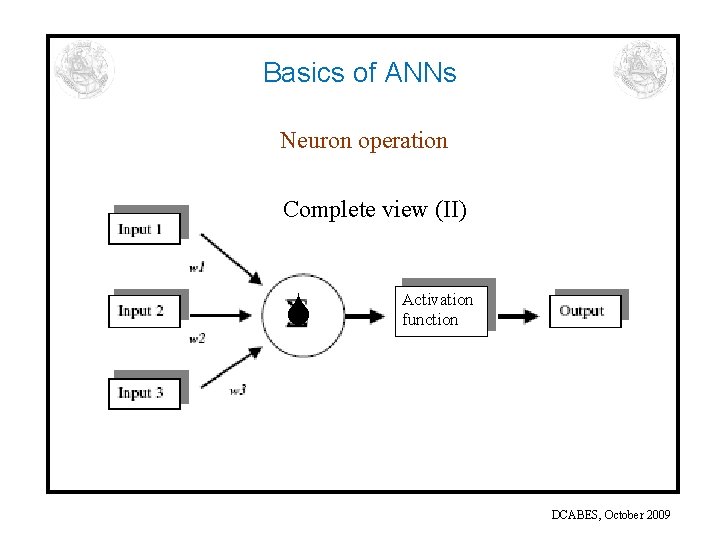
Basics of ANNs Neuron operation – Input signals – Weights denoting connection strengths multiply the input signals – The sum of the weighted inputs is sent through the neuron – It passes through a non-liner activation function – It is transferred to the output-used as input to output neighbouring units or units at a next layer DCABES, October 2009

Basics of ANNs Neuron operation Complete view (I) w Input ij i DCABES, October 2009

Basics of ANNs Neuron operation Complete view (II) Activation function DCABES, October 2009

Basics of ANNs Activation Function • Introduces non-linearity to a problem • Maps the neuron output to a required interval, usually [-1, 1] or [0, 1] • Commonly used activations functions: Activation Function Mathematical Expression Logistic Sigmoid Hyperbolic tangent f(x) = tanh(x) Gaussian f(x) = exp(-x 2 /2σ2 ) DCABES, October 2009

Basics of ANNs Weights • Very important for learning rate and accuracy of network • Too large or too small values at initialization may cause problems DCABES, October 2009

Basics of ANNs • • • Network Architecture Hidden Layers/Nodes The number of neurons in the input and output layers is dictated by the physics of the problem The number of hidden layers and the number of nodes in each layer is more art than science! More hidden layers make an ANN smarter More neurons per layer make an ANN more accurate Determined by the complexity of the problem and the number of patterns (pairs of input/output vectors) used for training the ANN DCABES, October 2009

Basics of ANNs Hidden Layers/Nodes Heuristics (I) • 1 or 2 HLs adequate for most problems • For the number of nodes various propositions: Ni : Number of inputs, No : Number of outputs, Np : number of training samples r [5, 10] related to the noise of the data DCABES, October 2009

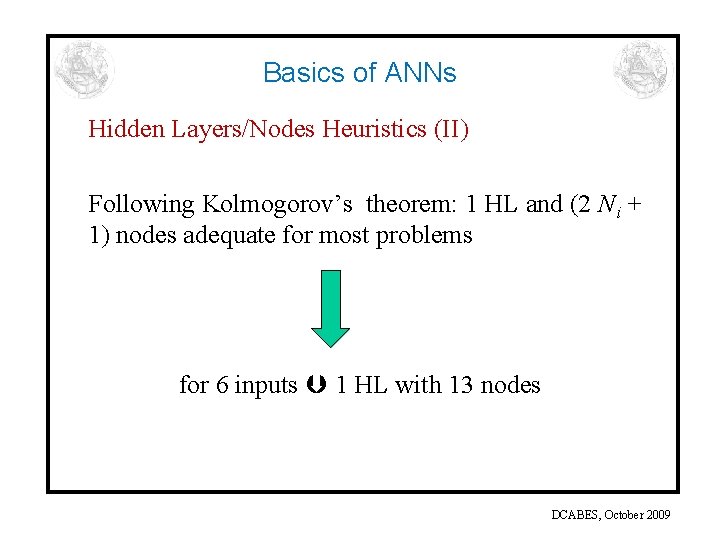
Basics of ANNs Hidden Layers/Nodes Heuristics (II) Following Kolmogorov’s theorem: 1 HL and (2 Ni + 1) nodes adequate for most problems for 6 inputs 1 HL with 13 nodes DCABES, October 2009

Basics of ANNs Learning Algorithm - Back Propagation (I) – The training process starts with a random distribution of the weights wij between layers passes through the nodes of the HLs a unique and wrong solution vector is yielded at the output. – a measure of the error can be calculated tk : correct output value, yk : predicted output value K: number of output neurons DCABES, October 2009

Basics of ANNs Learning Algorithm - Back Propagation (II) – Error minimization (Gradient Descent method) 0 – Thus, change in the output vector: – correction in weights: (n denoting iterations) – η: learning rate α: momentum term DCABES, October 2009

Basics of ANNs Learning Algorithm - Back Propagation (III) – Back propagation in a similar manner from output to hidden to input layers to determine all weights for each pattern, i. e. from output to hidden: – Then weights are determined: (hidden to output) (some intermediate weight) DCABES, October 2009

Basics of ANNs Learning Algorithm - Back Propagation (IV) – Process repeated for all patterns until an epoch is completed – At the end of each epoch, check for convergence (i. e. current error some small percentage of 1 st epoch error) IMPORTANT: Patterns during each epoch are randomly introduced (to avoid network memorising) – When convergence is achieved, the weights are stored and training is completed DCABES, October 2009

Basics of ANNs Learning Algorithm - Back Propagation (V) – Learning rate: determines the size of steps taken for error minimization – Momentum term: determines the direction of search In general: values of LR ~0. 2 and MT [0. 2, 0. 6] seem to be OK for the tests performed DCABES, October 2009

Basics of ANNs So far! • We have described a Feed Forward ANN with Back Propagation learning algorithm • ANNs with different architecture/learning algorithms do exist, i. e. : – Architecture: Architecture Feed Back (Recursive) networks- the output is fed back to the input layer in order to predict the following sequence – Learning: Learning Supervised (Radial Basis Function, Function Generalized Regression etc. ) or Unsupervised (Self Organizing Map, Map Adaptive Resonance Theory etc. ) BUT 95% of existing networks are FFBP!! DCABES, October 2009

Applications DCABES, October 2009

Application of ANN in rotorcraft aerodynamics DCABES, October 2009

Application of ANN in rotorcraft aerodynamics Description of the problem • Dynamic Stall : due to changes beyond a critical value in the angle of attack for a wing within an air stream • Vortices are generated on the surface which eventually detach and are shed downstream sudden loss of lift • Very important in rotorcraft aerodynamics, wind turbines etc. DCABES, October 2009

Application of ANN in rotorcraft aerodynamics DCABES, October 2009

Application of ANN in rotorcraft aerodynamics • Modelling approach of the problem involves solution in a very complex grid of the full Navier-Stokes viscous equations: where + Turbulence!! Reconstruction of the pressure field DCABES, October 2009

Application of ANN in rotorcraft aerodynamics Alternative approach • Construction of 2 NNs: one ANN and one RNN • Inputs: – angle of attack, ramp rate, 2 spatial coordinates, time (ANN) – angle of attack, ramp rate, previous timestep pressure coeffs (RNN) • Outputs: – Pressure coefficient: Cp = (p-p )/(2ρU 2 ) The pressure field may be reconstructed during pitching DCABES, October 2009

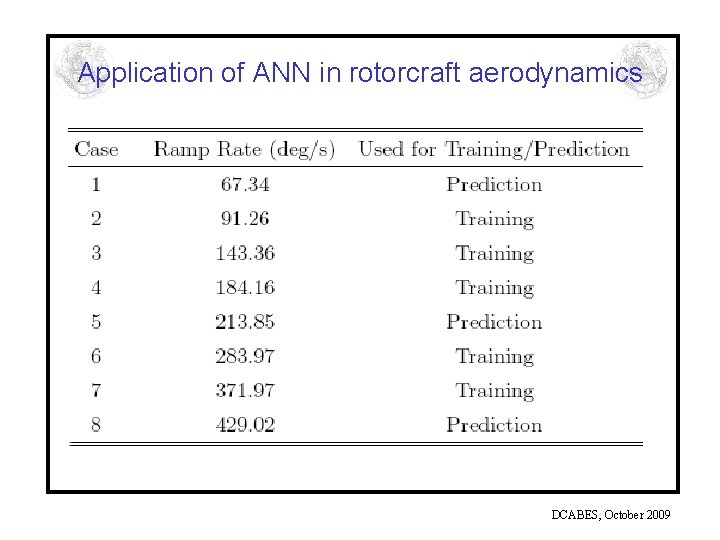
Application of ANN in rotorcraft aerodynamics • • Network specifics 2 HLs with 45 neurons in each layer Networks trained with available experimental data from 90 transducers covering the suction side of the wing. During every ramping case the angle of attack varied gradually from -50 to 390. Every case discretized in 150 steps. 67, 500 patterns used for training Convergence criterion: current error /initial error 1% Both interpolation and extrapolation (ramp rate values outside input training range) tested Training time 48 hrs in a 2. 6 GHz Linux box DCABES, October 2009

Application of ANN in rotorcraft aerodynamics DCABES, October 2009

Application of ANN in rotorcraft aerodynamics Extrapolation (Case 1 -low ramp rate)- 10 transducers on the wing leading edge DCABES, October 2009

Application of ANN in rotorcraft aerodynamics Interpolation (Case 5 -intermediate ramp rate)- 10 transducers on the wing leading edge DCABES, October 2009

Application of ANN in rotorcraft aerodynamics Extrapolation (Case 8 -high ramp rate)- 10 transducers on the wing leading edge DCABES, October 2009

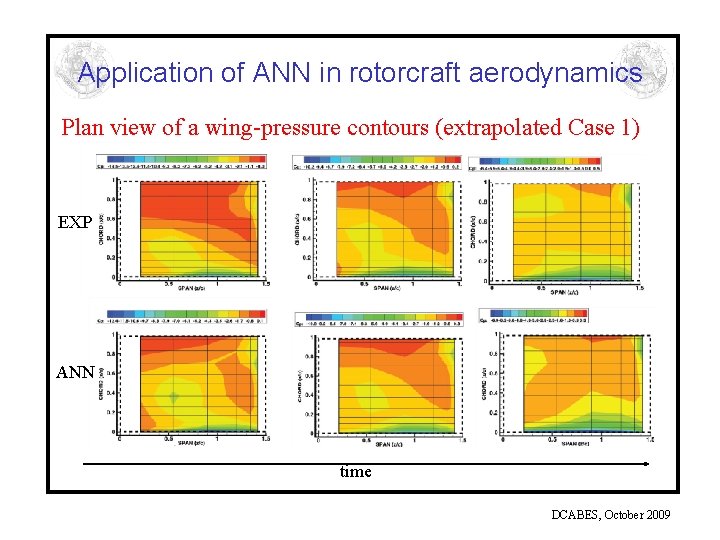
Application of ANN in rotorcraft aerodynamics Plan view of a wing-pressure contours (extrapolated Case 1) EXP ANN time DCABES, October 2009

Application of ANN in rotorcraft aerodynamics • • Both networks delivered very promising results. ANN performing slightly better than the RNN. Best comparison for the interpolated case (case 5) The NN seemed to predict very well the behaviour of Cp with 2% the largest discrepancy between the measured and predicted Cp values. • Small discrepancies due to a relative inability of the ANN to extrapolate away from its training regime or because the specific ramp rate training regime used was inadequate to provide the network with an ‘understanding’ of the physics of the flow outside this regime. DCABES, October 2009

Application of ANN in the prediction of stock prices – short-term trading DCABES, October 2009

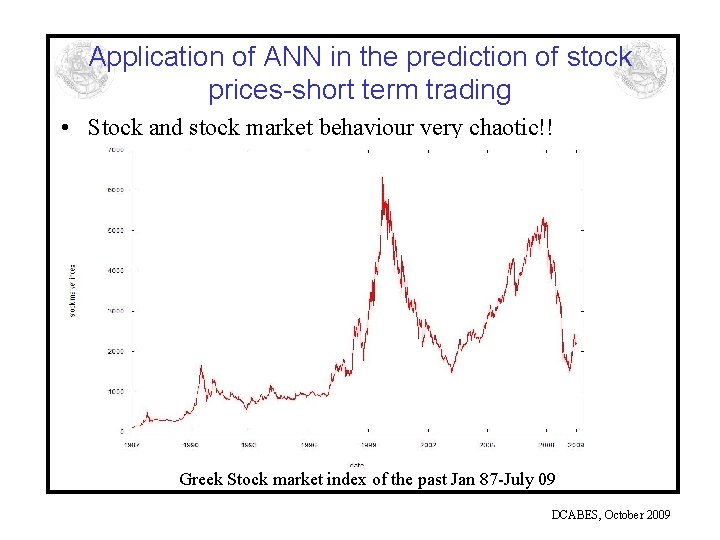
Application of ANN in the prediction of stock prices-short term trading • Stock and stock market behaviour very chaotic!! Greek Stock market index of the past Jan 87 -July 09 DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • There exist various tools and strategies – Technical Analysis (previous knowledge utilized to predict whether a stock will trend upward/downward) – mathematical models i. e. Black-Scholes PDE: St: stock price, Wt: Brownian term μ, σ: mean & standard deviation of a Gaussian • Both approaches have limitation due to simplifying assumptions and “averaging” behaviour ANN approach!! DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • • • Available data Daily closing price of a Greek bank stock Greek Stock market Index (GSI). Period of 5600 trading days(02/01/1987 -06/07/2009) Data exhibit very chaotic behaviour What should be fed in the ANN? Extraction of different training data set DCABES, October 2009

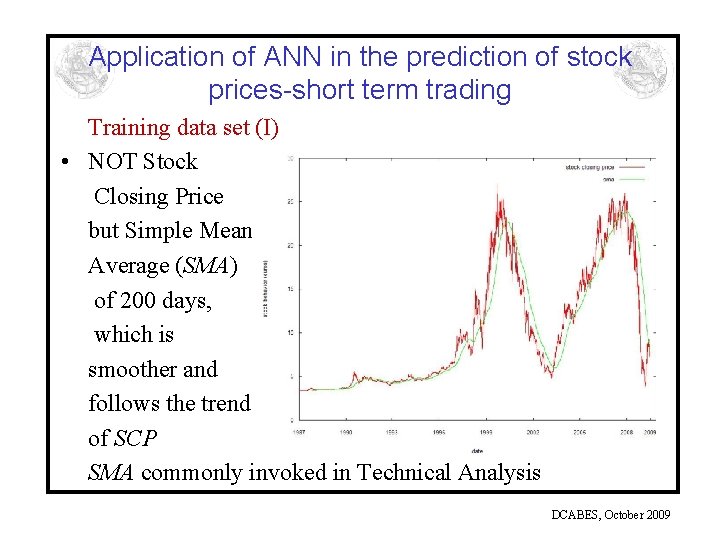
Application of ANN in the prediction of stock prices-short term trading Training data set (I) • NOT Stock Closing Price but Simple Mean Average (SMA) of 200 days, which is smoother and follows the trend of SCP SMA commonly invoked in Technical Analysis DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading Training data set (II) • NOT daily GSI but a market trend tied to the equivalent SMA • Weighted mean of all GSIs corresponding to the 200 days of each SMA (the bias is put towards the period closer to the corresponding SMA). Compared to standard mean DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading Training data set (III) • Comparison of Meanw and Means determines a trend for the Greek Stock market - GST – |Meanw-Means| 0. 15 Means stock market stability GST=0 – Meanw > 1. 15 Means stock market increase GST=1 – Meanw < 0. 85 Means stock market decrease GST=-1 Margin of 15% carefully chosen after many trials to represent the different periods of the Greek Stock market DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • • • Training data set (IV) Available SMAs split into 5 -day periods and an equivalent Overall Stock market Trend (OST) was found from the corresponding GSTs (by counting 0’s, 1’s and -1’s): – OST around zero: stock market stability – OST negative: stock market decrease – OST positive: stock market increase Pattern formation: 6 inputs (5 -day week SMAs + 1 OST) and 1 output (SMA of the first day of the following week) Total of 1080 patterns – 1000 used for training – 80 used for tests DCABES, October 2009

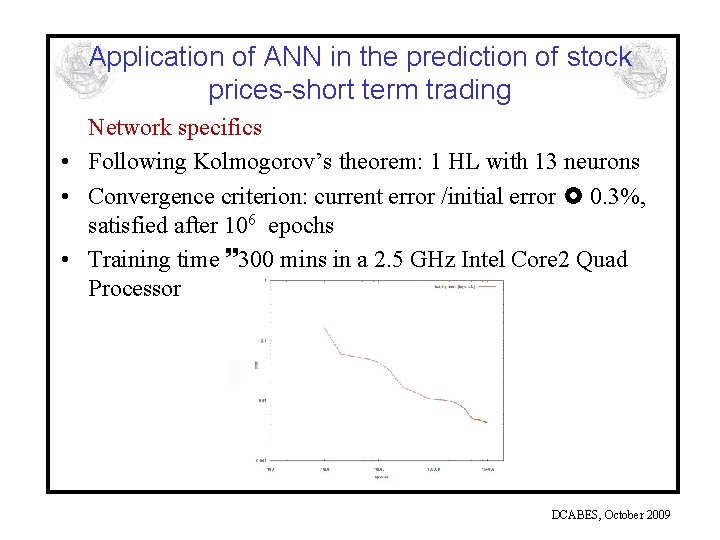
Application of ANN in the prediction of stock prices-short term trading Network specifics • Following Kolmogorov’s theorem: 1 HL with 13 neurons • Convergence criterion: current error /initial error 0. 3%, satisfied after 106 epochs • Training time 300 mins in a 2. 5 GHz Intel Core 2 Quad Processor DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • • Testing of the ANN fed with 1. 5 years’ data Asked to utilize one week’s SMA data and the corresponding OST to predict what will happen to the SMA for the following 2 weeks by using every time the data that had predicted for the following day!! For each group of data, the ANN ran 10 times predicting SMAs 10 days ahead and after the 5 th time, it relied solely on predicted data!! OST behaviour known a priori (first stability, then decrease) so it was fixed in all subsequent runs DCABES, October 2009

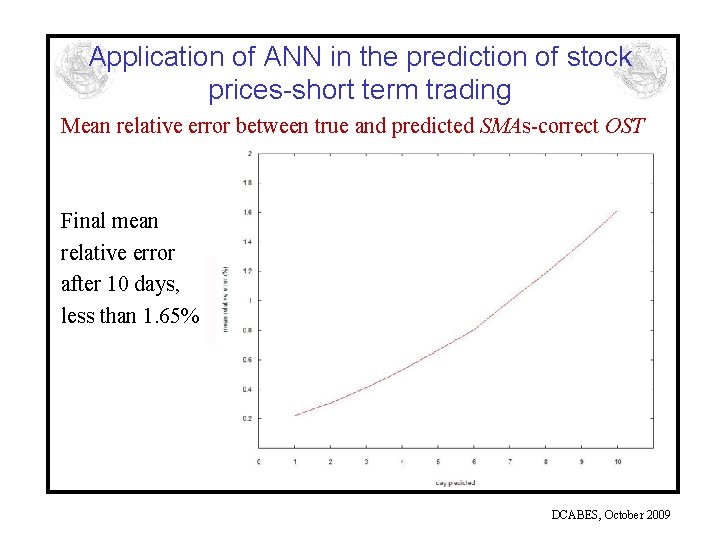
Application of ANN in the prediction of stock prices-short term trading Mean relative error between true and predicted SMAs-correct OST Final mean relative error after 10 days, less than 1. 65% DCABES, October 2009

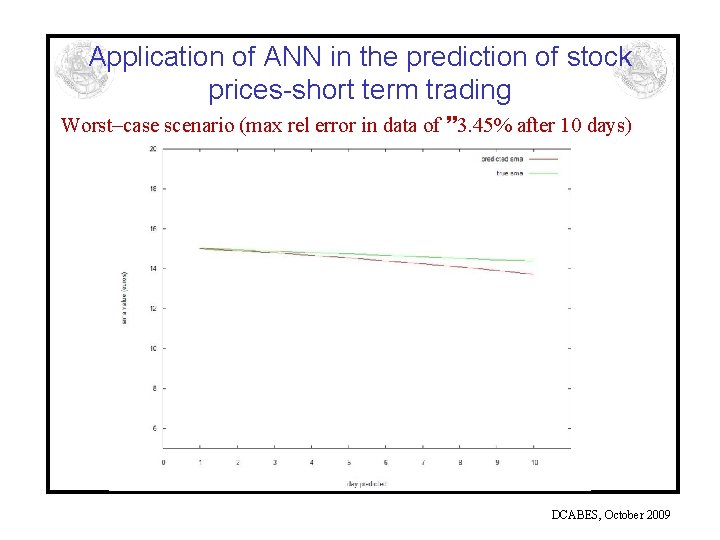
Application of ANN in the prediction of stock prices-short term trading Worst–case scenario (max rel error in data of 3. 45% after 10 days) DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading Test of OST in results • Runs with OST given by uniform random number generator Equal probability for an increase, decrease or stability pattern to emerge DCABES, October 2009

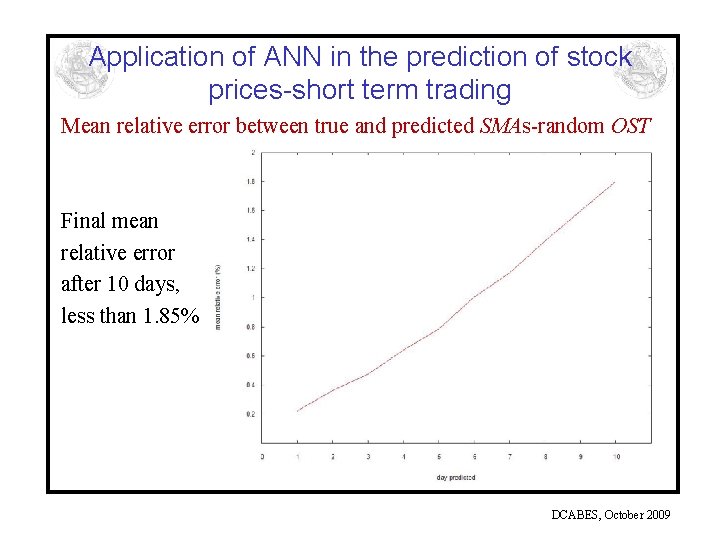
Application of ANN in the prediction of stock prices-short term trading Mean relative error between true and predicted SMAs-random OST Final mean relative error after 10 days, less than 1. 85% DCABES, October 2009

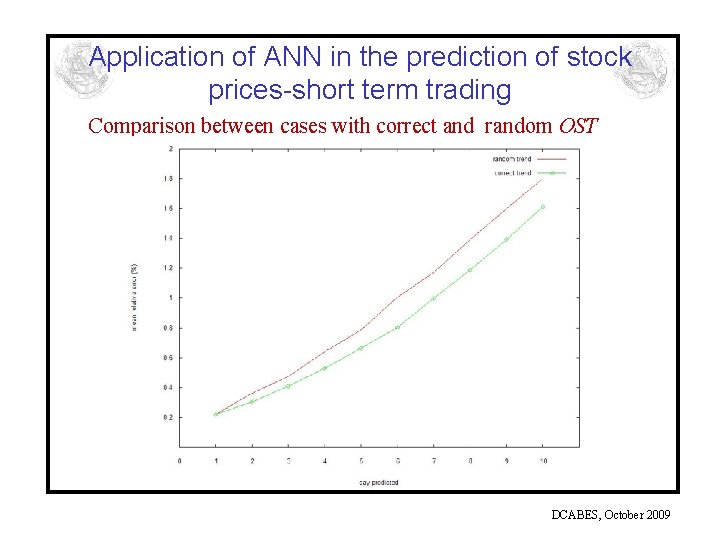
Application of ANN in the prediction of stock prices-short term trading Comparison between cases with correct and random OST DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • Quite good agreement!! • The results in both cases do not seem to be influenced by OST!! • Why? • Because bank stocks closely tied to the Stock market index and follow it very closely • Hence, indirect inclusion in the stock trend. • Of course more test required for a definitive conclusion! DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • • Further testing of the network The training data set was split into two equal parts The ANN was trained for the same conditions using either the first 500 patterns or the latter 500 patterns. Same network architecture retained Same processor used Same convergence criterion-converged after ~ 106 epochs Training time: 150 mins-exactly half of what it took before ANN then used to predict 10 days ahead as before DCABES, October 2009

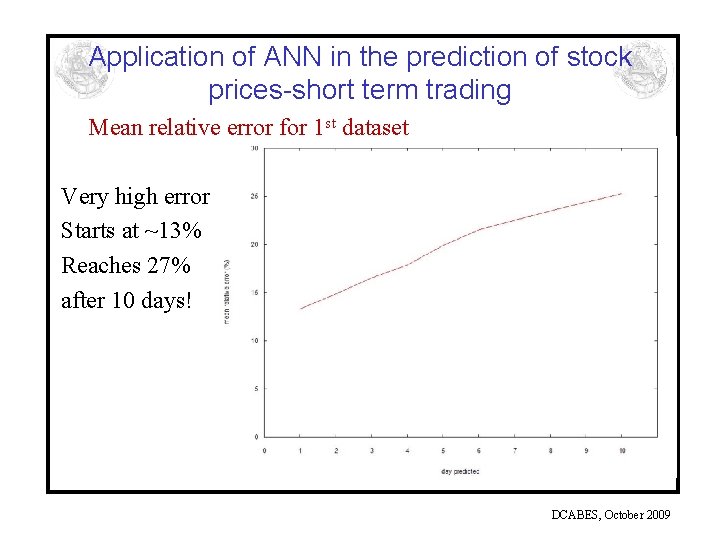
Application of ANN in the prediction of stock prices-short term trading Mean relative error for 1 st dataset Very high error Starts at ~13% Reaches 27% after 10 days! DCABES, October 2009

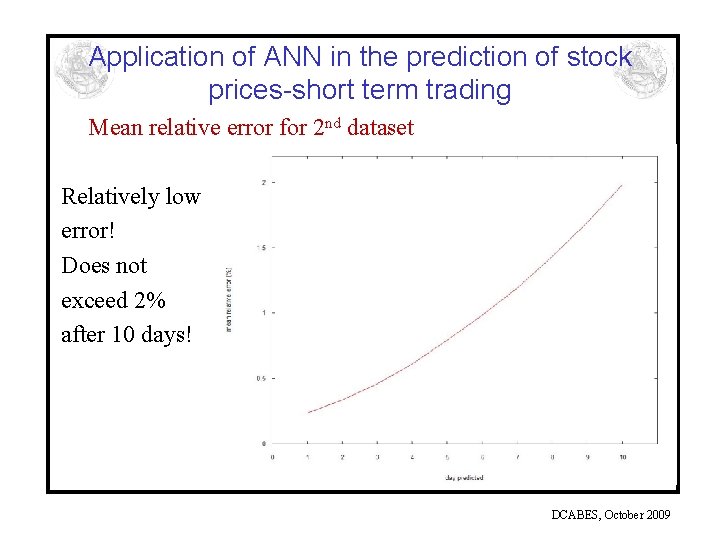
Application of ANN in the prediction of stock prices-short term trading Mean relative error for 2 nd dataset Relatively low error! Does not exceed 2% after 10 days! DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • Is this a paradox? DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • Is this a paradox? NO!! • In the 1 st dataset the maximum value of SMAs does not exceed a value of EU 15 and is asked to predict values of the order of EU 23 (the test runs are extrapolation) • In the 2 nd dataset training is performed for values higher than the required ones during testing (the test runs are interpolation) • ANNs in general are known to be problematic with extrapolation DCABES, October 2009

Application of ANN in the prediction of stock prices-short term trading • • • Conclusions This is on-going work So far, very promising results New approach to stock prediction via SMAs and determining a subsequent stock market trend Further testing is required, different network configurations to be tested ANNs have been proven to be suitable for the solution of many real problems where complexity of the system and non-linearity does not allow a complete mathematical / physical approach DCABES, October 2009

Thank you for your attention! DCABES, October 2009